научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2010
УДК. 004.8, 519.85
1. Введение в генетические алгоритмы
Генетический алгоритм (ГА) представляет собой эволюционный метод оптимизации, основанный на концепциях естественного отбора и генетики [1, стр. 2]. Идею ГА подсказала сама природа и работы Дарвина. В 1966 г. Л.Дж. Фогель, А.Дж. Оуэнс, М.Дж. Волш предложили и исследовали эволюцию простых автоматов, предсказывающих символы в цифровых последовательностях. В 1975 г. Дж.X. Холланд предложил схему генетического алгоритма. Эти работы легли в основу главных направлений разработки эволюционных алгоритмов. Простой генетический алгоритм был впервые описан Гольдбергом на основе работ Холланда.
Исходя из концепции естественного отбора и генетики делается предположение: если взять две жизнеспособных особи и каким-либо образом получить из них новую особь, то будет высокая вероятность того, что эта особь будет также жизнеспособная или даже более приспособленная к условиям существования. В генетических алгоритмах особи представлены в виде хромосом (бинарных векторов, решений), которые представляют собой закодированные специальным образом значения аргументов заданной целевой функции. Жизнеспособность (приспособленность к условиям существования) особей в ГА определяется с помощью функции пригодности (ФП)– целевой функции, способной принимать аргумент в виде бинарного вектора. Поэтому под пригодностью хромосомы в ГА понимается значение функции пригодности хромосомы. В генетических алгоритмах исходные решения представляют собой родительский пул или родительские хромосомы. Новые решения, получаемые из исходных решений, в ГА называются потомками. Процесс получения потомков из родительских хромосом реализуется в ГА с помощью операторов кроссинговера и мутации.
Для реализации генетического алгоритма используют моделирование эволюции (естественного отбора) или если проще - борьбы за выживание. В природе каждое животное стремится выжить, чтобы оставить после себя как можно больше потомства. Борьба за выживание в генетических алгоритмах представляет собой процесс замещения в популяции хромосом с худшей пригодностью на хромосомы с лучшей пригодностью, получаемые в результате скрещивания и мутации.
|
|
|
|
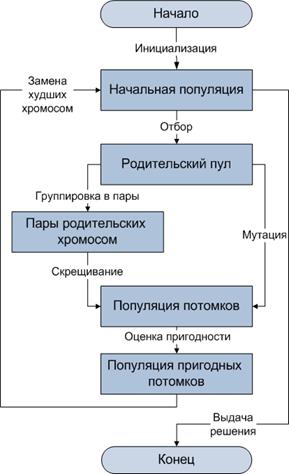
Рисунок 1 - Блок-схема генетического алгоритма
|
Рисунок 2 - Схема эволюции решений в генетическом алгоритме
|
Генетический алгоритм представляет собой искусственную эволюцию, включающую несколько этапов (рисунок 1): инициализацию популяции случайными хромосомами, отбор, группирование хромосом в пары, скрещивание и мутацию родительских хромосом, оценку пригодности потомков, проверку условий завершения поиска. При этом хромосомы начальной популяции в процессе эволюции замещаются другими, более приспособленными хромосомами (рисунок 2).
2. Разработка островного генетического алгоритма с динамическим распределением вероятностей выбора генетических операторов
2.1 Сущность идеи динамической самоорганизации параметров ГА
Для каждого этапа работы генетического алгоритма (рисунок 1) существуют свои генетические операторы (ГО). Так, скрещивание может быть реализовано с помощью генетических операторов: одноточечными, двухточечными и универсальными мультиточечными кроссинговерами. Отбор может быть: случайным, рулеточным, элитарным и т. д. Очевидно, что для конкретной целевой функции может быть наиболее эффективным только один строго определенный набор генетических операторов. Для этого исследователи производят выбор наиболее эффективных генетических операторов, при которых ГА обеспечивает наиболее быстрое получение оптимума для заданной целевой функции. Однако в жизни часто приходится сталкиваться с ситуациями, когда выражение целевой функции заранее неизвестно или это выражение меняется в процессе выполнения оптимизации («правила игры меняются в процессе игры»). В этой ситуации невозможно предугадать наиболее эффективные генетические операторы.
Динамическая самоорганизация параметров ГА позволяет разрешить эту проблему [1, стр. 14, 2 - 6]. При динамической самоорганизации параметров ГА в алгоритм встраивается несколько различных операторов в каждой группе генетических операторов (таблица 1). Каждый оператор в своей группе имеет равные вероятности появления. В каждой итерации алгоритма выбирается один из операторов для каждого этапа работы в соответствии с его вероятностью появления (рисунок 3). При этом фиксируются частоты появления прогрессивных хромосом (хромосом, превосходящих по пригодности лучшую хромосому в популяции), при использовании каждого из операторов. Данные частоты определяют в дальнейшем вероятность применения операторов. Таким образом, генетический алгоритм реализует механизм динамической самоорганизации параметров.
|
|
|
Рисунок 3 - Распределение вероятностей выбора генетических операторов в группе генетических операторов
|
Таблица 1 - Генетические операторы, соответствующие этапам работы ГА
|
|
Группы генетических операторов, соответствующие этапам работы ГА
|
||||
|
Селекция (отбор)
|
Группирование хромосом в пары
|
Скрещивание
|
Мутация
|
Оценка пригодности
|
|
|
Генетические операторы
|
10, 20, 30, 40, 50 и 60-процентные элитарные отборы [6, стр. 27]
|
инбридинг (узкородственное спаривание, инцест) [1, стр. 13]
|
одноточечный кроссинговер [8, стр. 138]
|
одноточечная мутация [8, стр. 134]
|
любая хромосома пригодна
|
|
аутбридинг (неродственное спаривание) [1, стр. 13]
|
двухточечный кроссинговер [8, стр. 161]
|
двухточечная мутация
|
|||
|
рулеточный отбор [8, стр. 137]
|
группирование лучшей хромосомы со всеми хромосомами родительского пула
|
универсальный мультиточечный кроссинговер [8, стр. 161]
|
полная мутация (инверсия) [8, стр. 162]
|
пригодность хромосомы лучше средней в популяции
|
|
|
группирование лучших хромосом с лучшими
|
25, 50 и 75-процентные мутации
|
||||
|
случайный отбор [8, стр. 159]
|
группирование всех хромосом со всеми
|
пригодность хромосомы лучше лучшей в популяции
|
|||
|
случайное группирование (панмиксия) [1, стр. 13]
|
|||||
2.2 Обоснование подхода к пересчету вероятностей выбора генетических операторов в группе генетических операторов
В данной работе в отличие от известных подходов к пересчету вероятностей выбора генетических операторов [1, стр. 14; 2 - 4] предлагается использовать их модификацию. Дело в том, что исследователя интересует не количество получаемых прогрессивных хромосом, а общее время поиска решения. Так, например, группирование пар хромосом с помощью инбридинга (узкородственного спаривания, инцеста) занимает время, пропорциональное квадрату размера родительского пула (при 128 хромосомах родительского пула время группирования хромосом инбридингом составляет около 12 миллисекунд на персональном компьютере со средней производительностью). Частота появления прогрессивных хромосом в результате инбридинга достаточно высокая (около 25 хромосом на 1000 сгруппированных в пары). В то же время группирование лучшей хромосомы со всеми остальными хромосомами из родительского пула занимает меньшее время (около 2 миллисекунд на 128 хромосом родительского пула) и дает приблизительно тот же результат (около 18 хромосом на 1000 сгруппированных). В связи с этим целесообразно чаще использовать оператор группирования лучшей хромосомы со всеми остальными, чем инбридинг. Это позволяет сократить общее время поиска решения приблизительно в 5 раз. Если для конкретной целевой функции окажется, что в начальный момент времени оператор группирования лучшей хромосомы со всеми остальными дает большее количество прогрессивных хромосом на единицу времени, чем инбридинг, а на конечном этапе наоборот, то отношение накапливаемого количества прогрессивных хромосом к накапливаемому времени для поиска этих хромосом позволит сместить баланс использования генетических операторов группирования в сторону инбридинга на конечном этапе работы алгоритма.
Также следует отметить, что если расчет целевой функции занимает значительное время, то изложенный подход также позволит производить глобальный поиск достаточно быстро, так как время работы генетического оператора включает время расчета целевой функции.
Математически данный подход можно описать следующим образом. Генетические операторы в отдельно взятой i-ой итерации ГА можно представить набором ![]() , где
, где ![]() - оператор селекции (S - selection),
- оператор селекции (S - selection), ![]() - оператор группирования хромосом в пары (G - grouping),
- оператор группирования хромосом в пары (G - grouping), ![]() - оператор скрещивания (R - reproduction),
- оператор скрещивания (R - reproduction), ![]() - оператор мутации (M - mutation),
- оператор мутации (M - mutation), ![]() - оператор оценки пригодности хромосомы (A - accepting).
- оператор оценки пригодности хромосомы (A - accepting).
Выполнение отдельно взятой i-ой итерации характеризуется временем ![]() выполнения преобразований с помощью операторов
выполнения преобразований с помощью операторов ![]() и количеством
и количеством ![]() полученных прогрессивных хромосом.
полученных прогрессивных хромосом.
Пусть имеется статистика ![]() и
и ![]() по
по ![]() итерациям ГА. Тогда методами факторного анализа можно получить оценки времени
итерациям ГА. Тогда методами факторного анализа можно получить оценки времени ![]() работы генетического оператора
работы генетического оператора ![]() и количества
и количества ![]() прогрессивных хромосом, получаемых с помощью оператора
прогрессивных хромосом, получаемых с помощью оператора ![]() .
.
Вероятность выбора оператора ![]() пропорциональна отношению среднего количества
пропорциональна отношению среднего количества ![]() прогрессивных хромосом, получаемых оператором
прогрессивных хромосом, получаемых оператором ![]() , к времени
, к времени ![]() работы оператора
работы оператора ![]()
; 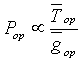 .
.
Для получения достоверных оценок времени работы ГО и количества прогрессивных хромосом необходимо иметь статистику значительного объема (![]() ). Однако в этом случае исчезает смысл динамического выбора генетических операторов, т.к. для динамического изменения вероятностей необходимо иметь статистику, которая в большинстве случаев будет получена позже, чем будет найден искомый глобальный экстремум. Таким образом, факторный анализ не позволяет оперативно выбирать наиболее эффективные генетические операторы.
). Однако в этом случае исчезает смысл динамического выбора генетических операторов, т.к. для динамического изменения вероятностей необходимо иметь статистику, которая в большинстве случаев будет получена позже, чем будет найден искомый глобальный экстремум. Таким образом, факторный анализ не позволяет оперативно выбирать наиболее эффективные генетические операторы.
Рассмотрим подход, основанный на непосредственной оценке времени работы каждого оператора и количества прогрессивных хромосом, получаемых этими операторами. Этот подход требует принятия ряда допущений о том, как рассчитывать количество прогрессивных хромосом, получаемых операторами отбора, группирования и оценки пригодности.
Допущение 1. Количество прогрессивных хромосом, получаемых операторами отбора, равно суммарному количеству прогрессивных хромосом, полученных последующим группированием в пары, скрещиванием и мутацией.
Допущение 2. Количество прогрессивных хромосом, получаемых операторами группирования хромосом в пары, равно количеству прогрессивных хромосом, полученных последующим скрещиванием.
Допущение 3. Количество прогрессивных хромосом, получаемых операторами оценки пригодности хромосом, равно количеству прогрессивных хромосом, полученных в следующей итерации ГА. Это позволяет отдать предпочтение тем операторам оценки пригодности хромосом, которые обеспечивают наискорейшее улучшение популяции.
Количество прогрессивных хромосом, получаемых с использованием генетического оператора ![]() , за единицу времени составляет величину:
, за единицу времени составляет величину:
; & nbsp;  ,
,
где ![]() - суммарное время работы генетического оператора
- суммарное время работы генетического оператора ![]() ,
, ![]() - общее количество прогрессивных хромосом, полученных генетическим оператором
- общее количество прогрессивных хромосом, полученных генетическим оператором ![]() с учетом допущений 1-3.
с учетом допущений 1-3.
Вероятность ![]() выбора генетического оператора определяется путем нормирования количества
выбора генетического оператора определяется путем нормирования количества ![]() прогрессивных хромосом, получаемых от использования генетического оператора, за единицу времени:
прогрессивных хромосом, получаемых от использования генетического оператора, за единицу времени:
; & nbsp;  ,
,
где ![]() - количество генетических операторов в группе, в которой принадлежит оператор
- количество генетических операторов в группе, в которой принадлежит оператор ![]() ;
; ![]() - количество прогрессивных хромосом, получаемых от использования
- количество прогрессивных хромосом, получаемых от использования ![]() -го генетического оператора в группе, за единицу времени.
-го генетического оператора в группе, за единицу времени.
Покажем, как будет работать механизм динамической выбора генетических операторов в группе генетических операторов. В таблице 2 приведен фрагмент динамического выбора генетических операторов в каждом поколении при поиске максимума двухпараметрической функции Растригина (см. приложение 2).
Черные стрелки в таблице 2 иллюстрируют принятые допущения. Первые итерации ГА позволяют накопить статистику для расчета вероятностей ![]() . При этом выбор операторов на данном этапе работы ГА случайный. После накопления статистики выбор генетических операторов определяется найденными вероятностями
. При этом выбор операторов на данном этапе работы ГА случайный. После накопления статистики выбор генетических операторов определяется найденными вероятностями ![]() . Из таблицы 2 видно, что в конце работы ГА преимущественно используются:
. Из таблицы 2 видно, что в конце работы ГА преимущественно используются:
- среди операторов отбора - 10-процентный элитарный отбор,
- среди операторов группирования хромосом в пары - группирование всех хромосом со всеми,
- среди операторов скрещивания - универсальный мультиточечный кроссинговер,
- среди операторов мутации - полная мутация,
- среди операторов оценки пригодности - оператор «пригодность хромосомы не менее средней пригодности в популяции».
|
Таблица 2 - Пример динамического выбора генетических операторов в группах генетических операторов
|
|
|
2.3 Реализация генетического алгоритма
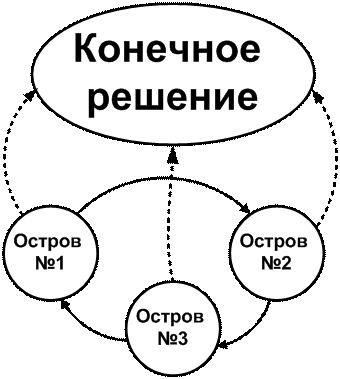
Используя результаты, полученные в [9], генетический алгоритм с динамическим распределением вероятностей выбора генетических операторов был включен в островную модель ГА с топологией «кольцо» (рисунок 4), как наиболее эффективной топологией островных моделей алгоритмов. Островные ГА позволяют улучшить надежность решений. Период миграций задается динамически: миграция хромосом из популяции в популяцию производится только тогда, когда хотя бы в одной из популяций длительно не улучшалось решение. Период времени для определения факта «длительное неулучшение решения» составляет 1/100 предельного времени работы ГА.
|
|
|
Рисунок 4 - Схема работы топологии «кольцо» островного генетического алгоритма при трех «островах»
|
При реализации генетического алгоритма была рассмотрена возможность сохранения значений рассчитанных функций пригодности. Однако, как показала практика, сохранение в базу данных одной записи занимает время, большее, чем время расчета самой целевой функции (для СУБД SQLite версии 3 время сохранения одной записи составляет ![]() сек., а вычисление ФП занимает
сек., а вычисление ФП занимает ![]() сек.), а вероятность повторного появления хромосомы (особенно на начальном этапе работы алгоритма) очень низкая (при длине хромосомы 256 генов вероятность составляет порядка
сек.), а вероятность повторного появления хромосомы (особенно на начальном этапе работы алгоритма) очень низкая (при длине хромосомы 256 генов вероятность составляет порядка ![]() ). Поэтому реализация контроллера готовых целевых функций и базы данных рассчитанных целевых функций оказалась нецелесообразной.
). Поэтому реализация контроллера готовых целевых функций и базы данных рассчитанных целевых функций оказалась нецелесообразной.
С разработанным генетическим алгоритмом можно ознакомиться на сайте свободного программного обеспечения по электронному адресу https://sourceforge.net/projects/insulargenetica/. Генетический алгоритм реализован в виде многопоточной кроссплатформенной библиотеки InsularGenetica под лицензией GNU Lesser GPL v.3, что не является препятствием для его свободного использования. Примеры приложений, использующих библиотеку InsularGenetica, также можно найти на сайте. На библиотеку InsularGenetica получено свидетельство о государственной регистрации программы для ЭВМ ╧ 2010610175 от 11 января 2010 г. в Федеральной службе по интеллектуальной собственности, патентам и товарным знакам (Роспатент). Это также не является препятствием для свободного использования в производных программных продуктах при условии упоминания в списке авторов производного продукта автора библиотеки InsularGenetica.
2.4 Оценка эффективности островного генетического алгоритма с динамическим распределением вероятностей выбора генетических операторов
Для проверки справедливости изложенных выше рассуждений в данной работе был проведён вычислительный эксперимент (таблица 3), в котором сравнивались известные генетические алгоритмы и островной генетический алгоритм с динамическим распределением вероятностей выбора генетических операторов (ОГА с ДРВ) по нескольким показателям нахождения алгоритмами квазиоптимального решения: по времени поиска, по количеству перебранных хромосом и количеству поколений популяции. Квазиоптимальным решением в данной работе приняты такие значения параметров двухпараметрической функции Растригина, при которых значения целевой функции находятся в диапазоне от -0,01 до 0,00 (приложение 2). В таблице 3 приведены средние значения и дисперсии соответствующих показателей, рассчитанные по 100 запускам алгоритмов каждого типа.
Анализ таблицы 3 показывает, что ГА с ДСП (алгоритм, взятый за основу при разработке ОГА с ДРВ) позволяет находить квазиоптимальные решения за меньшее по сравнению с ПГА число поколений популяции. Однако при этом количество перебранных хромосом более чем в 100 раз превышает аналогичный показатель ПГА. По этой же причине время поиска квазиоптимального решения существенно возрастает. ГА с ДСП является универсальным алгоритмом для поиска оптимальных решений для любых целевых функций, т.к. позволяет экономить время исследователя на подбор наиболее эффективных генетических операторов. В связи с этим время работы ГА с ДСП является величиной, равносильной времени работы других ГА, если учесть трудозатраты исследователя на подбор наиболее эффективных операторов и частот для конкретных целевых функций. ГА с ДСП является более обобщенным и потенциально более эффективным в задачах где: а) нет возможности проводить предварительный эксперимент по подбору операторов, или б) где сама задача имеет динамическую природу (правила игры меняются в ходе игры).
Таблица 3 - Результаты тестирования генетических алгоритмов
|
Генетический алгоритм
|
Время поиска квазиоптимального решения
|
Количество обращений к целевой функции
|
Количество поколений популяции
|
|||
|
ср., сек.
|
дисп.,сек.2
|
ср.
|
дисп.
|
ср.
|
дисп.
|
|
|
ПГА
|
29,9
|
592,4
|
1267039,3
|
1,017·1012
|
74,9
|
3584,5
|
|
ГА с РВКиМ
|
26,4
|
670,3
|
1114035,7
|
9,152·1011
|
89,4
|
5600,2
|
|
ГА с КиМ в
каждом поколении
|
15,6
|
284,9
|
780658,9
|
6,156·1011
|
237,7
|
586007,6
|
|
ГА с ДСП
|
54,2
|
1360,1
|
1925972,8
|
2,469·1012
|
68,4
|
1226,7
|
|
ОГА с ДРВ (1 остров)
|
9,5
|
13,2
|
359432,9
|
1,467·1010
|
-
|
-
|
|
ОГА с ДРВ (2 острова)
|
12,0
|
16,9
|
560247,8
|
2,113·1010
|
-
|
-
|
|
ОГА с ДРВ (3 острова)
|
19,7
|
37,4
|
859917,7
|
5,173·1010
|
-
|
-
|
|
ОГА с ДРВ (4 острова)
|
23,9
|
48,6
|
1130073,4
|
6,433·1010
|
-
|
-
|
|
ОГА с ДРВ (5 островов)
|
31,6
|
81,1
|
1357689,2
|
9,944·1010
|
-
|
-
|
Примечания:
1. ПГА - простой генетический алгоритм [10, 11].
2. ГА с РВКиМ - ГА с регуляцией вероятностей кроссинговера и мутации [5].
3. ГА с КиМ в каждом поколении - ПГА, в котором операторы мутации и скрещивания работают в каждом поколении и применяются ко всем хромосомам родительского пула.
4. ГА с ДСП - ГА с динамической самоорганизацией параметров с распределением вероятностей выбора генетических операторов в каждой группе операторов [1, стр. 14].
5. ОГА с ДРВ - островной ГА с динамическим распределением вероятностей выбора генетических операторов.
6. Количество поколений популяции оценивалось факультативно для неостровных ГА.
ГА с КиМ в каждом поколении показал лучшие результаты по сравнению с близким к нему и более адаптируемым ГА с КиМ. Этот факт можно объяснить сложностью функции Растригина. Очевидно, большое количество мутаций обеспечило более быстрое достижение квазиоптимального значения.
ОГА с ДРВ с одним островом позволяет в 3 раза быстрее находить квазиоптимальное решение по сравнению с ПГА. При этом перебирается в 3 раза меньшее количество хромосом. Следует также отметить высокую надежность решений, получаемых ОГА с ДРВ - дисперсия времени поиска квазиоптимального решения с помощью ОГА с ДРВ меньше, чем у остальных ГА. Из таблицы 3 видно, что островной генетический алгоритм с динамическим определением периода миграций и динамической регуляцией вероятностей выбора генетических алгоритмов показывает относительно хорошие результаты и для большего числа островов. Это позволяет позиционировать ОГА с ДРВ как наиболее подходящий алгоритм поиска квазиоптимальных решений целевых функций, расчет которых занимает продолжительное время.
2.5 Проверка сходимости островного генетического алгоритма с динамическим распределением вероятностей выбора генетических операторов
Сходимость реализации любых методов оптимизации базируется на известной теореме Вейерштрасса [12]. Сходимость канонического генетического алгоритма доказана в теореме Холланда (схем, шаблонов) [8]. В то же время любые модификации генетических алгоритмов, отличные от канонического алгоритма, подлежат тщательной проверке. Для генетических алгоритмов существует 2 общепризнанных способа доказать сходимость:
1. доказать теорему схем для созданной модификации ГА;
2. проверить работу ГА на известных ЦФ с известными областями определений, значений, локальными и глобальными экстремумами.
Идею анализа генетических алгоритмов для определения их эффективности предложил Де Йонг (De Jong) в своей работе [13]. Суть идеи заключается в том, что эффективность генетического алгоритма проверяется на задаче поиска оптимума ряда тестовых целевых функций.
В работе проверка сходимости проводилось вторым способом - путем тестирования ГА на известных ЦФ. В связи с этим практические задачи в работе не рассматриваются. Сформулируем требования к набору целевых функций. Эти требования должны обеспечить всестороннее тестирование реализации генетического алгоритма. Итак, набор целевых функций должен включать:
- функции с одним и несколькими глобальными и локальными экстремумами;
- непрерывные функции и функции с разрывами;
- функции с непрерывными и дискретными аргументами;
- детерминированные и стохастические функции;
- статические (координаты глобального максимума не изменяются) и динамические функции (координаты глобального максимума зависят от времени).
В приложении 2 приведен набор функций, совокупно отвечающих заданным требованиям, кроме дискретности принимаемых аргументов. В то же время генетический алгоритм оперирует дискретными решениями - бинарными векторами (хромосомами), которым можно противопоставить вектора непрерывных значений аргументов ЦФ по известным правилам [8, стр. 139-144] с заданным разбиением допустимого диапазона значений каждого из аргументов ЦФ на подинтервалы. Таким образом, требование дискретности аргументов ЦФ также выполняется для выбранного набора ЦФ, приведенных в приложении 2.
В таблице 4 и на рисунке 5 показаны результаты тестирования ОГА с ДРВ на различных тестовых функциях. Остановка эволюции по предельному времени поиска не применялась. Каждое значение в таблице 4 и каждая точка на рисунке 5 получены усреднением результатов по 100 запусках алгоритма. Математическое выражение используемых в таблице 4 функций приведено в приложении 2. Тестирование проводилось при длине хромосомы 256 генов (взято условно). Размер популяции по рекомендациям из различных источников был выбран равным 128 хромосом. Следует отметить, что в таблице 4 и на рисунке 5 не приведена динамическая двухпараметрическая функция Cyrcle. Анализ сходимости при тестировании ГА на данной ЦФ приведен ниже.
|
|
|
Рисунок 5 - Надежность ОГА с ДРВ
|
Таблица 4 - Надежность ОГА с ДРВ
|
Целевая функция
|
Диапазон квазиоптимальных значений
|
Надежность ОГА с ДРВ в зависимости от количества островов
|
||||
|
1
|
2
|
4
|
8
|
16
|
||
|
Растригина 2 перем.
|
-0,001…0,000
|
0,93
|
0,98
|
1,00
|
1,00
|
1,00
|
|
Растригина 10 перем.
|
-0,005…0,000
|
0,32
|
0,65
|
0,88
|
0,97
|
1,00
|
|
Растригина 2 перем., инверт.
|
>80,706
|
0,91
|
0,93
|
0,99
|
1,00
|
1,00
|
|
Растригина 10 перем., инверт.
|
>403,532
|
0,96
|
0,99
|
1,00
|
1,00
|
1,00
|
|
De Jong 2 перем.
|
1,001…1,002
|
0,12
|
0,35
|
0,69
|
0,88
|
1,00
|
|
De Jong 5 перем.
|
25
|
0,95
|
0,98
|
1,00
|
1,00
|
1,00
|
|
Griewank 2 перем.
|
-0,001…0,000
|
0,66
|
0,86
|
1,00
|
1,00
|
1,00
|
|
Griewank 10 перем.
|
-0,005…0,000
|
0,44
|
0,66
|
0,78
|
0,88
|
0,95
|
|
Gaussian quartic 2 пер.
|
>1370
|
0,91
|
0,97
|
0,98
|
1,00
|
1,00
|
|
Gaussian quartic 2 пер. инвер.
|
>-2
|
0,97
|
0,99
|
1,00
|
1,00
|
1,00
|
|
Gaussian quartic 10 пер.
|
>6872
|
0,86
|
0,92
|
0,94
|
1,00
|
1,00
|
|
Gaussian quartic 10 пер. инвер.
|
>-10
|
0,90
|
0,92
|
0,98
|
1,00
|
1,00
|
|
Среднее арифметическое:
|
0,74
|
0,85
|
0,94
|
0,98
|
1,00
|
|
Примечания: 1) для функции De Jong (5 переменных) алгоритм запускался на поиск оптимального решения, т.к. данная функция является ступенчатой в гиперпространстве; 2) для стохастических целевых функций Gaussian quartic диапазон квазиоптимальных значений выбран достаточно широким, что обусловлено наличием случайных величин в выражении целевых функций.
Данные в таблице 4 показывают надежность получаемых решений с помощью островной модели генетического алгоритма. При этом под надежностью решения в данной работе понимается отношение количества запусков генетического алгоритма, при которых алгоритм сошелся к квазиоптимальному решению, к общему числу запусков алгоритма.
Результаты тестирования ОГА с ДРВ на 12 различных целевых функциях (приложение 2, таблица 4, рисунок 5) позволяют утверждать, что разработанный алгоритм является наиболее универсальным алгоритмом для поиска оптимальных значений априорно неизвестных целевых функций. При этом при увеличении числа островов удается существенно повысить надежность получаемых решений.
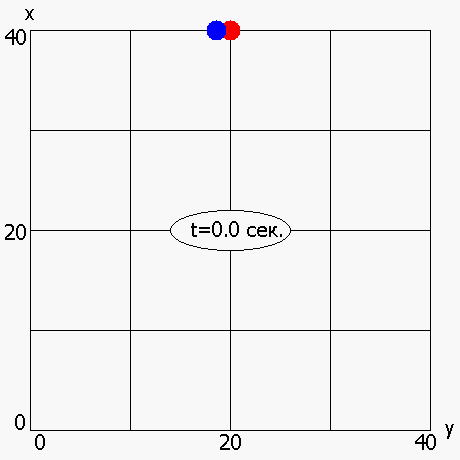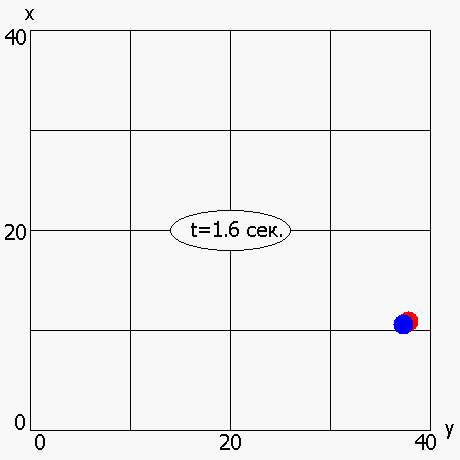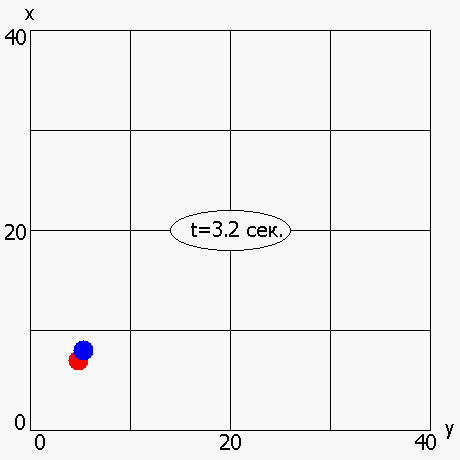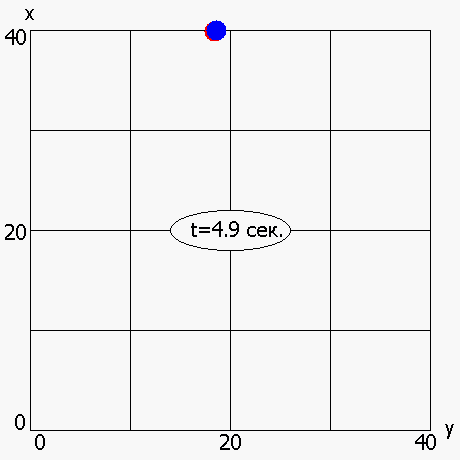
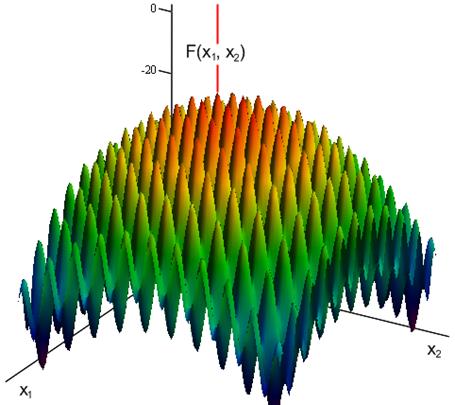
В работе также была рассмотрена мультимодальная динамическая двухпараметрическая целевая функция Cyrcle (приложение 2), график которой приведен на рисунке 6. Период «обращения» функции Cyrcle составляет 5 секунд. ОГА с ДРВ позволяет динамически отслеживать изменение целевой функции (рисунок 7) и находить координаты глобального максимума (или близкие к нему координаты) в каждый момент времени.
|
|
|
|
Рисунок 6 - Распределение значений двухпараметрической динамической целевой функции Cyrcle в зависимости от времени
|
Рисунок 7 - Динамическое изменение оптимума, полученного ОГА с ДРВ, в зависимости от времени: красная точка –глобальный максимум; синяя точка - максимум, полученный ОГА с ДРВ
|
2.6 Исследование динамического выбора генетических операторов
Ниже представлены результаты работы реализованного генетического алгоритма на примере известных целевых функций (Растригина и De Jong). Для всех запусков генетического алгоритма, для всех тестовых целевых функций справедливо утверждение о том, что для длины хромосомы 256 генов и размера популяции 128 хромосом оптимальное решение находится после перебора приблизительно 10000000 хромосом (при размере пространства поиска ![]() ). Рассматривалась как конкретная эволюция популяции, так и изменение вероятностей выбора генетических операторов в процессе эволюции.
). Рассматривалась как конкретная эволюция популяции, так и изменение вероятностей выбора генетических операторов в процессе эволюции.
2.6.1 Исследование механизма динамического выбора генетических операторов при максимизации функции Растригина
Тестирование алгоритма на функции Растригина для случая двух переменных представлено на графиках рисунков 9 - 14 (первые 100 поколений). График функции Растригина приведен на рисунке 8. Математическое выражение и характеристики двухпараметрической функции Растригина представлены в приложении 2.
|
|
|
Рисунок 8 - График двухпараметрической функции Растригина
|
По оси абсцисс на графиках рисунков 9 - 14 отложены количество перебранных хромосом (рисунок 9) и время эволюции (рисунки 10 - 14). Конкретные значения на шкалах рисунков соответствуют друг другу во временном срезе. Так например, значению 400000 перебранных хромосом на рисунке 9 соответствуют время работы 16:07:01 на рисунках 10 - 14.
|
|
|
|
Рисунок 9 - Зависимость значений функции пригодности в популяции от количества потомков
|
Рисунок 10– Зависимость соотношения вероятностей выбора операторов селекции от времени эволюции
|
|
|
|
|
Рисунок 11 - Зависимость соотношения вероятностей выбора операторов группирования от времени эволюции
|
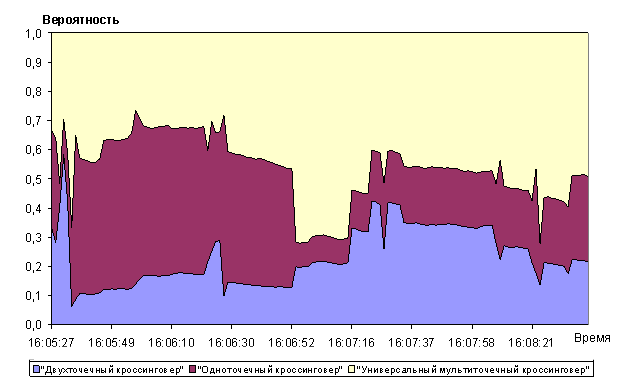
Рисунок 12 - Зависимость соотношения вероятностей выбора операторов скрещивания от времени эволюции
|
|
|
|
|
Рисунок 13 - Зависимость соотношения вероятностей выбора операторов мутации от времени эволюции
|
Рисунок 14 - Зависимость соотношения вероятностей выбора операторов оценки пригодности хромосом от времени эволюции
|
Анализ рисунков 9 - 14 показывает, что алгоритм позволяет достаточно быстро находить глобальный максимум мультимодальной функции Растригина. Сходимость к квазиоптимальному решению (абсолютная ошибка не более 0,01) была получена перебором всего 600 000 хромосом при полной размерности пространства перебора ![]() хромосом. Сходимость к оптимальному решению была получена при переборе 9,5 млн. хромосом.
хромосом. Сходимость к оптимальному решению была получена при переборе 9,5 млн. хромосом.
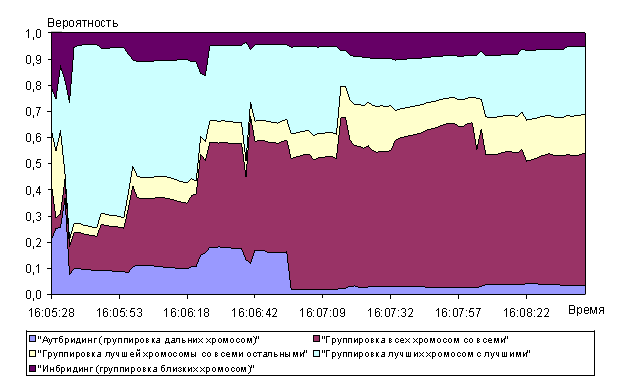
Среди операторов отбора преимущественно использовался 10-процентный элитарный отбор (рисунок 10), что обусловлено высокой вероятностью получения прогрессивных хромосом в результате скрещивания и низкими затратами машинного времени. Случайный отбор, как и следовало ожидать, не получил высокого приоритета, т.к. в соответствии с теоремой Холланда при случайном отборе вероятность выживания хорошей схемы ниже, чем при рулеточном или элитарном отборе. Рулеточный отбор также не получил высокого приоритета, т.к. его использование в отличие от остальных операторов отбора отнимает большее машинное время.
Наибольший приоритет среди операторов группирования хромосом в пары получил оператор группирования всех хромосом со всеми (рисунок 11). Это обусловлено тем, что преимущественно использовался элитарный отбор хромосом. В связи с этим любой из способов группирования хромосом «элиты» даст с высокой вероятностью хорошее потомство. Также следует отметить, что оператор аутбридинг имел достаточно высокий приоритет в начале эволюции до 50-го поколения (время на оси абсцисс 16:06:23 на графике рисунка 11) и низкий после 50-го поколения. Таким образом обеспечивался в начале эволюции поиск промежуточных локальных максимумов на рисунке 8. После нахождения самых высоких экстремумов функции Растригина оператор аутбридинг перестал «приносить» прогрессивные хромосомы.
Универсальный мультиточечный кроссинговер показывал относительную стабильность и высокий приоритет использования в алгоритме среди операторов скрещивания (рисунок 12). Операторы одно- и двухточечный кроссинговер имеют два чётких участка (до и после 50-го поколения, время на оси абсцисс 16:06:23 на графике рисунка 12), на которых их вероятность выбора уменьшается (одноточечный кроссинговер) в 2 раза и увеличивается (двухточечный кроссинговер) в 2 раза.
Полная мутация также показала высокую стабильность и наибольшую вероятность отбора (рисунок 13). Возможно, полная мутация позволила искать прогрессивные хромосомы в иных относительно сформированной популяции областях пространства поиска.
При включении хромосомы, обладающей пригодностью лучше лучшей в популяции, в популяцию удалось добиться высокой вероятности получения прогрессивных хромосом в следующем поколении (рисунок 14). «Плато» до 25-го поколения в графиках вероятностей операторов оценки пригодности обусловлено тем, что за это время (25 поколений, соответствующие времени 16:06:14 на графике рисунка 14) производилась предварительная оценка вероятностей отбора. Дело в том, что в реализации алгоритма используются в первую очередь те генетические операторы, которые ранее еще не выбирались. Тем самым обеспечивается использование всех генетических операторов, хотя и с разной вероятностью выбора.
2.6.2 Исследование механизма динамического выбора генетических операторов при максимизации функции De Jong
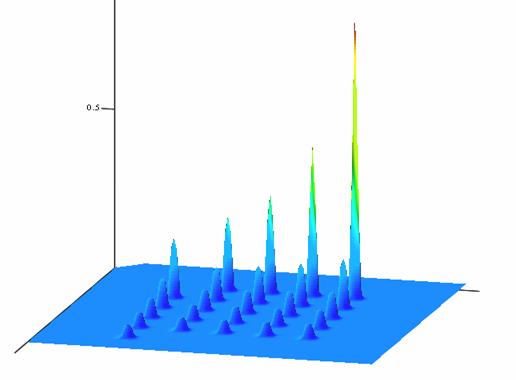
График двухпараметрической функции De Jong представлен на рисунке 15. Тестирование алгоритма на функции De Jong представлено на графиках рисунков 16 - 21 (первые 70 поколений). Математическое выражение и характеристики двухпараметрической функции De Jong представлено в приложении 2.
|
|
|
Рисунок 15 - График двухпараметрической функции De Jong
|
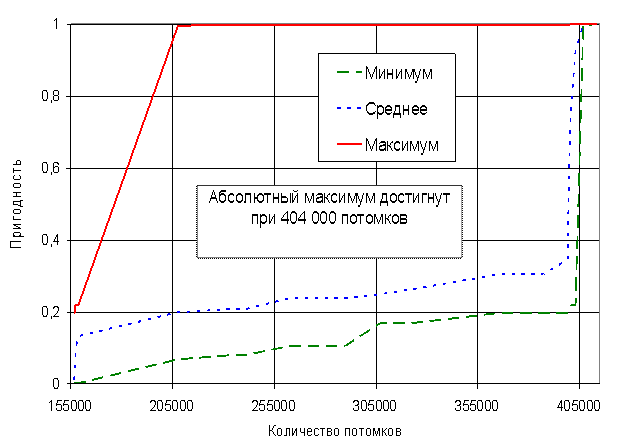
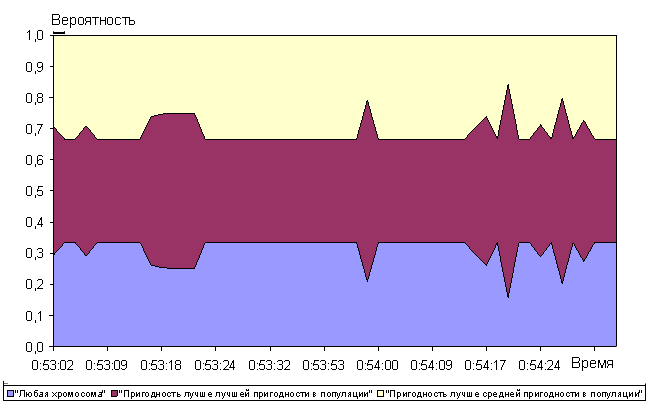
По оси абсцисс на графиках рисунков 16 - 21 отложены количество перебранных хромосом (рисунок 16) и время эволюции (рисунки 17 - 21). Конкретные значения на шкалах рисунков соответствуют друг другу во временном срезе. Так, например, значению 405000 перебранных хромосом на рисунке 16 соответствуют время работы 00:54:32 на рисунках 17 - 21.
|
|
|
|
Рисунок 16 - Зависимость значений функции пригодности в популяции от количества потомков
|
Рисунок 17 - Зависимость соотношения вероятностей выбора операторов селекции от времени эволюции
|
|
|
|
|
Рисунок 18 - Зависимость соотношения вероятностей выбора операторов группирования от времени эволюции
|
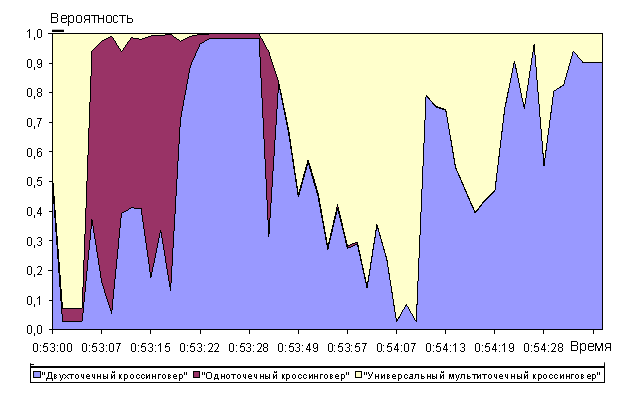
Рисунок 19 - Зависимость соотношения вероятностей выбора операторов скрещивания от времени эволюции
|
|
|
|
|
Рисунок 20 - Зависимость соотношения вероятностей выбора операторов мутации от времени эволюции
|
Рисунок 21 - Зависимость соотношения вероятностей выбора операторов оценки пригодности хромосом от времени эволюции
|
Анализ рисунков 16 - 21 показывает, что алгоритм позволяет достаточно быстро находить глобальный максимум мультимодальной функции De Jong. Сходимость к квазиоптимальному решению (абсолютная ошибка не более ![]() ) была получена перебором всего 210 000 хромосом (при полной размерности пространства перебора
) была получена перебором всего 210 000 хромосом (при полной размерности пространства перебора ![]() хромосом). Сходимость к оптимальному решению была получена при переборе 404 000 хромосом.
хромосом). Сходимость к оптимальному решению была получена при переборе 404 000 хромосом.
Среди операторов отбора также как в случае функции Растригина преимущественно использовался 10-процентный элитарный отбор (рисунок 17). Наибольший приоритет среди операторов группирования хромосом в пары получили с переменным успехом оператор группирования всех хромосом со всеми и оператор группирования лучших хромосом с лучшими. Это обусловлено тем, что преимущественно использовался элитарный отбор хромосом. В связи с этим любой из способов группирования хромосом «элиты» даст с высокой вероятностью прогрессивное потомство. Также следует отметить, что оператор аутбридинг имел достаточно высокий приоритет в начале эволюции до 0:53:10 на графике рисунка 18 и низкий позже. Таким образом обеспечивался в начале эволюции поиск промежуточных локальных максимумов на рисунке 15. Время 0:53:10 на графике 18 соответствует достижению квазиоптимального решения (210 000 перебранных хромосом на графике рисунка 16). После нахождения самых высоких экстремумов функции De Jong (рисунок 16) оператор аутбридинг перестал «приносить» прогрессивные хромосомы. Среди операторов скрещивания нельзя четко выделить наиболее и наименее эффективный, т.к. в разные моменты времени все виды кроссинговера имели самый высокий приоритет. Среди операторов мутации также нельзя четко выделить наиболее или наименее эффективные. При включении в популяцию хромосомы, обладающей пригодностью лучше лучшей в популяции, в популяцию удалось добиться высокой вероятности получения прогрессивных хромосом в следующем поколении (рисунок 21). Однако оператор оценки пригодности «Пригодность хромосомы лучше лучшей в популяции» в случае функции De Jong не имел существенного преимущества как в функции Растригина оператор «Пригодность хромосомы лучше средней в популяции».
3. Заключение
1. Изучение механизма динамической самоорганизации параметров генетического алгоритма по идее Бюргера Ю.А. позволило усовершенствовать подход к динамическому выбору наиболее эффективных генетических операторов, изменив способ пересчета вероятностей выбора генетических операторов.
2. Разработанный алгоритм показал высокую эффективность в сравнении с известными генетическими алгоритмами.
3. Использование в алгоритме топологии «кольцо» островных генетических алгоритмов оказалось оправданным, т.к. при увеличении количества островов удалось существенно повысить надежность получаемых решений для нескольких известных целевых функций. Это позволяет утверждать, что алгоритм будет давать не менее надежные решения и для других ранее неизвестных целевых функций.
4. Впервые было проведено исследование процессов, протекающих внутри генетического алгоритма с динамическим выбором генетических операторов при эволюции. Исследованию были подвергнуты такие изменяющиеся составляющие генетического алгоритма, как начальная популяция и вероятности выбора генетических операторов в зависимости от времени эволюции и характера целевой функции. Механизм динамической самоорганизации параметров генетического алгоритма реализует при работе логику выбора генетических операторов, обеспечивающую высокую эффективность работы алгоритма для различных целевых функций, изменение распределения вероятностей выбора генетических операторов при изменении ЦФ.
Список использованных источников
1. Бюргер Ю.А. Мягкие вычисления. Статья по материалам конференции fido7.ru.algorithms // Электронный документ http://incubos.by.ru/docs/genetic.doc
2. Петров Ю.Ю. Применение генетического алгоритма с регуляцией вероятностей генетических операторов при решении задачи упаковки в контейнеры // Сборник научных трудов СевКавГТУ. Серия «Естественнонаучная». 2006. ╧ 2. Северо-Кавказский государственный технический университет, http://www.ncstu.ru/.
3. Jeong I.K., Lee J.J. Evolving Multi-Agents using a Self-Organizing Genetic Algorithm // Applied Mathematics and Computation, Volume 88, Number 2, 30 December 1997, pp. 293-303(11).
4. Jeong I.K., Lee J.J. A self-organizing genetic algorithm for multimodal function optimization // Springer ( Japan ): Artificial Life and Robotics, Vol.2, No.1, pp.48-52, mar. 1998
5. Петров Ю.Ю. Регуляция вероятностей кроссинговера и мутации // Инфотелекоммуникационные технологии в науке, производстве и образовании. Первая международная научно-техническая конференция. Ставрополь: СевКавГТУ, 2004 г.
6. Петров Ю.Ю. Управляемые генетические алгоритмы, основанные на статистике. // Вторая Всероссийская научная конференция «Нечеткие системы и мягкие вычисления». г. Ульяновск. http://nsmv2008.ulstu.ru/index.php?url=68&type=file 2008 г.
7. Панченко Т.В. Генетические алгоритмы. Под ред. Тарасевича Ю.Ю. // г.Астрахань: Издательский дом «Астраханский университет». mathmod.aspu.ru/images/File/ebooks/GAfinal.pdf, 2007 г. - 88с.
8. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. Рудинский И.Д. - М.: Горячая линия - Телеком, 2006 г. - 452с.
9. Литвиненко В.И., Бюргер Ю.А., Мирошник А.В. Сравнительная характеристика работы распределенных генетических алгоритмов. // Научный журнал «РадЁоелектронЁка. Iнформатика. Керування». Выпуск ╧ 1. Украина: Запорожский национальный технический университет - г.Запорожье - 2001 г.
10. Holland J.H. Adaptation in Natural and Artificial Systems. Ann Arbor: The University of Michigan Press, 1975 - 210 р.
11. Goldberg D.E. Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley Publishing Company, Inc. 1989, 412 р.
12. Лопатников Л.И. Экономико-математический словарь: Словарь современной экономической науки. - 5-е изд., перераб. и доп. - М.: Дело, 2003. - 520 с.
13. DeJong K.A. An analysis of the behavior of a class of genetic adaptive systems // Ph.D. dissertation, Univ. Michigan, Ann Arbor, MI, 1775
Приложение 1. Глоссарий
|
Термин
|
Определение
|
|
Бинарный вектор
|
вектор конечной длины, компоненты которого могут принимать значения из множества {0;1}
|
|
Ген
|
компонент бинарной строки.
|
|
Генетический алгоритм (ГА)
|
интеллектуальное исследование произвольного поиска
|
|
Генетический оператор (ГО)
|
оператор, позволяющий применить принципы естественного отбора и генетического наследования к виртуальной популяции
|
|
Группа генетических операторов
|
совокупность генетических операторов, объединенных по функциональному назначению
|
|
Кроссинговер
|
получение новой хромосомы путем обмена одинаковых участков хромосом родителей.
|
|
Лучшая хромосома
|
хромосома из популяции, превосходящая по пригодности остальные хромосомы в популяции.
|
|
Мутация
|
произвольная модификация одного или нескольких генов в хромосоме
|
|
Поколение
|
одна итерация работы генетического алгоритма.
|
|
Популяция
|
множество хромосом, обрабатываемых в текущей итерации
|
|
Потомки
|
хромосомы, полученные в результате скрещивания и мутации хромосом родительского пула.
|
|
Пригодность
|
значение функции пригодности
|
|
Прогрессивная хромосома
|
хромосома, не входящая в популяцию и превосходящая по пригодности лучшую хромосому в популяции
|
|
Пространство поиска
|
множество всех возможных решений
|
|
Решение
|
1) аргументы целевой функции (в контексте целевой функции); 2) бинарный вектор (в контексте функции пригодности)
|
|
Родительский пул
|
хромосомы, отобранные из популяции для дальнейшего скрещивания и мутации
|
|
Сходимость
|
свойство алгоритма (метода) обеспечивать нахождение решения поставленной задачи.
|
|
Точка поискового пространства
|
то же самое, что и решение.
|
|
Функция пригодности (ФП)
|
целевая функция, преобразованная для использования в генетическом алгоритме.
|
|
Хромосома
|
закодированные в бинарный вектор значения аргументов ЦФ.
|
|
Целевая функция (ЦФ)
|
скалярная функция одного или нескольких аргументов, связывающая цель (оптимизируемую переменную) с управляемыми переменными (аргументами) в задаче оптимизации
|
Приложение 2. Описание целевых функций
|
Функция, описание
|
Математическое выражение
|
Область определения
|
Координаты глобального максимума
|
|
Растригина 2 переменных,
1 глоб. и
|
|
|
|
|
Растригина 2 переменных, инверт.*
4 глоб. и 96 локал. максимумов, непрерывная
|
|
|
|
|
Растригина 10 переменных,
1 глоб. и
|
|
|
|
|
Растригина 10 переменных, инверт.*
|
|
|
|
|
De Jong 2 переменных,
1 глоб. и 25. лок. максимумов, непрерывная
|
где
|
|
|
|
De Jong 5 переменных,
непрерывное множество глоб. максимумов, непрерывная
|
где
|
|
|
|
Gaussian quartic 2 переменных
1 глоб. и 4 лок. максимума, непрерывная стохастическая
|
|
|
|
|
Gaussian quartic 2 переменных инверт.*
1 глоб. (он же лок.) максимум, стохастическая непрерывная
|
|
|
|
|
Gaussian quartic 10 переменных
1 глоб. и
|
|
|
|
|
Gaussian quartic 10 переменных инверт.*
1 глоб. и
|
|
|
|
|
Griewank 2 переменных
1 глоб. и 4 лок. максимума, непрерывная
|
|
|
|
|
Griewank 10 переменных
1 глоб. и множество лок. максимума, непрерывная
|
|
|
|
|
Cyrcle 2 переменных
1 глоб. и множество лок. максимумов, непрерывная, динамическая, период - 5 секунд
|
где
|
|
|
Примечание. * - инвертированные целевые функции представляют собой оригинальные целевые функции, умноженные на «-1». Это позволяет решать задачу минимизации оригинальной целевой функции, не меняя алгоритма, настроенного на решение задач максимизации целевых функций.
[1] СУБД - система управления базами данных
Публикации с ключевыми словами: генетический алгоритм
Публикации со словами: генетический алгоритм
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||