научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2009
DOI: 10.7463/0209.0115086
УДК 519.6
МГТУ им. Н.Э.Баумана,
sokolov@bmstu.ru,
karpenko@pk6.bmstu.ru,
galiamova@bmstu.ru
1. Введение
Современные обучающие системы представляют собой интеллектуальные системы, построенные на основе парадигмы обработки знаний. При этом формализация онтологии предметной области выполняется в виде базы знаний, которая может быть реализована на основе одной из следующих моделей знаний: продукционная модель; семантическая сеть; фреймовая модель; формальная логическая модель.
В работе полагается, что база знаний обучающей системы построена на основе семантической сети, содержащей понятия предметной области изучаемой дисциплины и отношения между этими понятиями. Указанная семантическая сеть представляется в виде ориентированного графа, вершины которого соответствуют понятиям предметной области изучаемой дисциплины, а дуги (рёбра) задают отношения между ними.
При обучении обычной является ситуация, когда субъект обучения удовлетворительно представляет детали изучаемого курса, но не владеет понятийным составом дисциплины в целом. Такая ситуация, очевидно, не позволяет интерпретировать уровень усвоения дисциплины как удовлетворительный. Поэтому важной задачей современной обучающей системы является поддержка изучения и контроля усвоения обучаемым понятий предметной области изучаемой дисциплины [1].
Для формализации представлений субъект обучения о понятийном составе изучаемой дисциплины в работе предлагается использовать когнитивные карты [2]. Каждая из этих карт формализует представления обучаемого о некотором понятии в виде графа, в идеале представляющего собой соответствующий подграф семантической сети изучаемой дисциплины. Контроль усвоения обучаемым некоторого понятия предметной области сводится к сравнению указанного подграфа семантической сети и графа, который определяет соответствующая когнитивная карта обучаемого [3].
Отметим следующее обстоятельство. Одним из центральных понятий инженерии онтологий [4] является понятие «отображение онтологий» (ontology mapping), под которым понимается деятельность по установлению соответствия между несколькими онтологиями или, другими словами, нахождение семантических связей подобных элементов из разных онтологий. Рассматриваемый в работе подход к контролю понятийных знаний субъекта обучения можно рассматривать в контексте проблемы отображения онтологий.
Используемая в работе модель семантической сети обучающей системы рассмотрена в работах [5, 6]. В данной работе рассматривается модель представлений субъекта обучения о понятиях изучаемой дисциплины в виде соответствующих когнитивных карт, а также некоторые метрики сравнения подграфов семантической сети изучаемой дисциплины и соответствующих графов, которые определяют когнитивные карты субъекта обучения.
Реализация предлагаемой методики предполагается в инструментальной обучающей системе БИГОР [7].
2. Постановка задачи
Входным понятием (inputconcept) данного модуля рассматриваемого учебного курса называется понятие, определение которого дано в некотором другом модуле данного или иного учебного курса. Аналогично, выходным понятием (outputconcept) данного модуля называется понятие ![]() , определение которого дано в данном модуле.
, определение которого дано в данном модуле.
Каждое из выходных понятий ![]() определяется через входные понятия модуля и/или другие его выходные понятия. Указанные входные и выходные понятия модуля называются информационно связанными с понятием
определяется через входные понятия модуля и/или другие его выходные понятия. Указанные входные и выходные понятия модуля называются информационно связанными с понятием ![]() в широком смысле [5]. Совокупность всех понятий, информационно связанных с понятием
в широком смысле [5]. Совокупность всех понятий, информационно связанных с понятием ![]() , включая само этот понятие, обозначается
, включая само этот понятие, обозначается ![]() . Количество понятий в наборе
. Количество понятий в наборе ![]() полагается равным
полагается равным ![]() .
.
Для каждого из понятий ![]() определена его сложность
определена его сложность ![]() . Сложность понятия
. Сложность понятия ![]() может назначаться конструктором курса или вычисляться обучающей системой, например, на основе мер сложности понятий, предложенных в работе [5]. Совокупность сложностей всех понятий множества
может назначаться конструктором курса или вычисляться обучающей системой, например, на основе мер сложности понятий, предложенных в работе [5]. Совокупность сложностей всех понятий множества ![]() обозначается
обозначается ![]() .
.
На множестве понятий ![]() определен набор отношений
определен набор отношений ![]() , где
, где ![]() - отношение «определяемое понятие – определяющее понятие» [3]. Набор отношений, связывающих между собой понятия
- отношение «определяемое понятие – определяющее понятие» [3]. Набор отношений, связывающих между собой понятия ![]() ,
, ![]() обозначается
обозначается ![]() , где всегда
, где всегда ![]() . Совокупность отношений, связывающих между собой все понятия набора
. Совокупность отношений, связывающих между собой все понятия набора ![]() , обозначается
, обозначается ![]() . Количество отношений в наборе
. Количество отношений в наборе ![]() полагается равным
полагается равным ![]() . Заметим, что в число отношений
. Заметим, что в число отношений ![]() не обязательно входят все отношения
не обязательно входят все отношения ![]() .
.
Для каждого из отношений ![]() конструктором данного модуля задана мера его «важности»
конструктором данного модуля задана мера его «важности» ![]() , формализующая «вес» данного отношения по сравнению с другими отношениями. Полагается, что
, формализующая «вес» данного отношения по сравнению с другими отношениями. Полагается, что ![]() для любых
для любых ![]() . Совокупность мер важности всех отношений, связывающих понятия
. Совокупность мер важности всех отношений, связывающих понятия ![]() , где
, где ![]() , а также совокупность мер важностей всех отношений
, а также совокупность мер важностей всех отношений ![]() обозначаются
обозначаются ![]() ,
, ![]() , соответственно.
, соответственно.
Семантическая сеть ![]() понятия
понятия ![]() определяется совокупностью понятий
определяется совокупностью понятий ![]() , мерами сложности этих понятий
, мерами сложности этих понятий ![]() , множеством отношений
, множеством отношений ![]() , а также мерами их важностями
, а также мерами их важностями ![]() :
:
![]() .
.
Семантическая сеть ![]() представляется в виде взвешенного ориентированного мультиграфа без контуров
представляется в виде взвешенного ориентированного мультиграфа без контуров ![]() , вершины которого соответствуют понятиям сети
, вершины которого соответствуют понятиям сети ![]() ; дуги – отношениям, связывающим эти понятий между собой; веса вершин – сложностям соответствующих понятий; веса дуг – важностям соответствующих отношений.
; дуги – отношениям, связывающим эти понятий между собой; веса вершин – сложностям соответствующих понятий; веса дуг – важностям соответствующих отношений.
Ставится следующая задача:
· разработать модель представлений субъекта обучения о заданной семантической сети ![]() в виде соответствующей когнитивной карты
в виде соответствующей когнитивной карты ![]() ;
;
· предложить метрики сравнения семантической сети ![]() и семантической сети, которую определяет когнитивная карта
и семантической сети, которую определяет когнитивная карта ![]() , формализующие уровень усвоения субъектом обучения понятия
, формализующие уровень усвоения субъектом обучения понятия ![]() .
.
3. Модель когнитивной карты
Первоначально термин «когнитивная карта» возник в психологии в рамках изучения особенностей познания человеком своего окружения. В этом случае под когнитивной картой понимается формализованное некоторым образом субъективное представление человека о пространственной организации окружающего мира [2]. В более широком смысле когнитивная карта не связывается с пространственной ориентацией человека, а формализует его представления о какой-либо проблемной области, т.е. представляет собой некоторый образ внутренних представлений человека об этой предметной области.
Основными элементами когнитивной карты являются базисные факторы (другие названия - факторы, концепты, параметры, переменные) и отношения между ними. Когнитивные карты принято представлять в виде графов, вершины которых соответствуют факторам, а ребра – отношениям между ними.
Определим когнитивную карту ![]() , соответствующую понятию
, соответствующую понятию ![]() , кортежем
, кортежем
![]() .
.
Здесь ![]() - набор понятий, включая понятие
- набор понятий, включая понятие ![]() , которые в когнитивной карте
, которые в когнитивной карте ![]() указаны, как связанные с понятием
указаны, как связанные с понятием ![]() ;
; ![]() - набор отношений из числа отношений
- набор отношений из числа отношений ![]() , которые в когнитивной карте
, которые в когнитивной карте ![]() связывают понятия набора
связывают понятия набора ![]() между собой. Количество понятий в наборе
между собой. Количество понятий в наборе ![]() обозначим
обозначим ![]() , а количество отношений в наборе
, а количество отношений в наборе ![]() -
- ![]() . Отметим, что, вообще говоря,
. Отметим, что, вообще говоря, ![]() ,
, ![]() .
.
Когнитивная карта ![]() представляется в виде ориентированного мультиграфа без контуров
представляется в виде ориентированного мультиграфа без контуров ![]() , вершины которого соответствуют понятиям
, вершины которого соответствуют понятиям ![]() , а дуги – отношениям
, а дуги – отношениям ![]() .
.
Предполагается, что указанная информация, содержащаяся в когнитивной карте ![]() , тем или иным образом получена от субъекта обучения.
, тем или иным образом получена от субъекта обучения.
4. Метрики качества обучения
Метрика ![]() качества усвоения субъектом обучения понятия
качества усвоения субъектом обучения понятия ![]() представляет собой меру близости графа
представляет собой меру близости графа ![]() семантической сети
семантической сети ![]() и графа
и графа ![]() , определяемого когнитивной картой
, определяемого когнитивной картой ![]() .
.
Можно предложить множество таких метрик, как использующих меры сложности понятий ![]() и меры важности отношений
и меры важности отношений ![]() , так и не использующие их.
, так и не использующие их.
4.1. Метрики, не использующие мер сложности и важности.
1). Метрика ![]() представляет собой количество понятий
представляет собой количество понятий ![]() из набора
из набора ![]() , содержащихся в наборе
, содержащихся в наборе ![]() , т.е.
, т.е.
![]()
![]() . (1)
. (1)
Величина ![]() есть ни что иное, как количество понятий, которые верно указанны субъектом обучения в качестве информационно связанных с понятием
есть ни что иное, как количество понятий, которые верно указанны субъектом обучения в качестве информационно связанных с понятием ![]() .
.
2). Метрика ![]() есть взвешенная разность между количеством верно указанных понятий
есть взвешенная разность между количеством верно указанных понятий ![]() и количеством
и количеством ![]() таких же неверно указанных понятий:
таких же неверно указанных понятий:
![]()
![]() . (2)
. (2)
Здесь ![]() - весовой множитель. Заметим, что в число неверно указанных понятий следует включать, как понятия из набора понятий
- весовой множитель. Заметим, что в число неверно указанных понятий следует включать, как понятия из набора понятий ![]() , не входящие в набор
, не входящие в набор ![]() , так и понятия из набора
, так и понятия из набора ![]() , не входящие в набор
, не входящие в набор ![]() .
.
Отметим, что метрика (2) и другие аналогичные метрики являются, по сути, двухкритериальными и вещественный весовой множитель ![]() определяет веса соответствующих частных критериев оптимальности.
определяет веса соответствующих частных критериев оптимальности.
3). Метрика ![]() аналогична метрике
аналогична метрике ![]() и является ни чем иным, как количеством верных отношений
и является ни чем иным, как количеством верных отношений ![]() из набора
из набора ![]() , содержащихся в наборе
, содержащихся в наборе ![]() :
:
![]()
![]() . (3)
. (3)
4). Метрика ![]() аналогична метрике
аналогична метрике ![]() и представляет собой взвешенную разность между количеством верно указанных отношений
и представляет собой взвешенную разность между количеством верно указанных отношений ![]() и количеством таких же неверно указанных отношений
и количеством таких же неверно указанных отношений ![]() :
:
![]()
![]() . (4)
. (4)
Здесь, аналогично формуле (2), ![]() - весовой множитель. В число неверно указанных отношений следует включать, как отношения из набора отношений
- весовой множитель. В число неверно указанных отношений следует включать, как отношения из набора отношений ![]() , не входящие в набор
, не входящие в набор ![]() , так и отношения из набора
, так и отношения из набора ![]() , не входящие в набор
, не входящие в набор ![]() . Кроме того, в число неверно заданных отношений следует включать отношения, которые в когнитивной карте связывают неверно заданные понятия.
. Кроме того, в число неверно заданных отношений следует включать отношения, которые в когнитивной карте связывают неверно заданные понятия.
5). Метрика ![]() является аддитивной сверткой метрик (1) – (4), т.е.
является аддитивной сверткой метрик (1) – (4), т.е.
![]() . (5)
. (5)
Здесь ![]() - весовой множитель.
- весовой множитель.
Значения метрик (1) – (4) имеют, вообще говоря, разные знаки и масштаб. Поэтому в метрике (5) целесообразно использовать нормированные значения указанных метрик
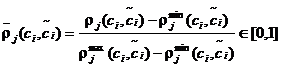 ,
, ![]() . (6)
. (6)
Здесь ![]() ,
, ![]() - минимально и максимально возможные значения метрик (1) – (4) соответственно. Легко видеть, что
- минимально и максимально возможные значения метрик (1) – (4) соответственно. Легко видеть, что
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
На основе нормированных метрик ![]() ,
, ![]() легко построить различные линейные и нелинейные бальные шкалы оценок. К примеру, M-бальная линейная шкала (
легко построить различные линейные и нелинейные бальные шкалы оценок. К примеру, M-бальная линейная шкала (![]() ) имеет вид, представленный в Табл. 1, где
) имеет вид, представленный в Табл. 1, где ![]() .
.
Таблица 1. К построению 5-бальной линейной шкалы оценок
Балл | Диапазон значений |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
Замечание 1. Можно предложить значительное количество метрик, которые являются модификациями рассмотренных метрик. Так в метрике (2) можно раздельно (с разными весовыми множителями) учитывать понятия, входящие в набор ![]() , но не входящие в набор
, но не входящие в набор ![]() , а также понятия, не входящие в набор
, а также понятия, не входящие в набор ![]() , но входящие в набор
, но входящие в набор ![]() . Аналогично, в метрике (4) раздельно можно учитывать три сорта отношений:
. Аналогично, в метрике (4) раздельно можно учитывать три сорта отношений:
· отношения из набора отношений ![]() , не входящие в набор
, не входящие в набор ![]() ;
;
· отношения из набора ![]() , не входящие в набор
, не входящие в набор ![]() ;
;
· отношения, которые в когнитивной карте связывают неверно заданные понятия![]()
4.2. Метрики, использующие меры сложности и важности.
6). Метрика ![]() аналогична метрике (1) и являет собой взвешенное количество верных понятий из набора
аналогична метрике (1) и являет собой взвешенное количество верных понятий из набора ![]() :
:
![]() ,
, ![]() . (7)
. (7)
Здесь ![]() - совокупность номеров верных понятий из набора
- совокупность номеров верных понятий из набора ![]() (количество таких номеров, очевидно, равно
(количество таких номеров, очевидно, равно ![]() ).
).
7). Метрика ![]() аналогична метрике (2) и имеет смысл разности взвешенных количеств верно и неверно указанных понятий из набора
аналогична метрике (2) и имеет смысл разности взвешенных количеств верно и неверно указанных понятий из набора ![]() :
:
![]() ,
, ![]() ; (8)
; (8)
![]() - весовой множитель;
- весовой множитель; ![]() - совокупность номеров неверных понятий из набора
- совокупность номеров неверных понятий из набора ![]() (количество этих номеров равно
(количество этих номеров равно ![]() ).
).
8). Метрика ![]() аналогична метрике (3) и есть ни что иное, как взвешенное количество верных отношений из набора
аналогична метрике (3) и есть ни что иное, как взвешенное количество верных отношений из набора ![]() :
:
![]() ,
, ![]() . (9)
. (9)
Здесь ![]() - совокупность номеров верных отношений из набора
- совокупность номеров верных отношений из набора ![]() , количество которых равно
, количество которых равно ![]() .
.
9). Метрика ![]() аналогична метрике (4) и имеет смысл разности взвешенных количеств верно и неверно указанных отношений из набора
аналогична метрике (4) и имеет смысл разности взвешенных количеств верно и неверно указанных отношений из набора ![]() :
:
![]() ,
, ![]() . (10)
. (10)
Здесь ![]() - весовой множитель; если
- весовой множитель; если ![]() , то
, то ![]() - неверное отношений из набора
- неверное отношений из набора ![]() . Общее количество номеров в наборе
. Общее количество номеров в наборе ![]() , где
, где ![]() , равно, очевидно,
, равно, очевидно, ![]() .
.
10). Метрика ![]() является аддитивной сверткой метрик (7) – (10):
является аддитивной сверткой метрик (7) – (10):
![]() . (11)
. (11)
Здесь ![]() - весовой множитель.
- весовой множитель.
Как и метрики (1) – (4), метрики (7) – (10) имеют, вообще говоря, разный масштаб. Поэтому и в метрике (11) целесообразно использовать аналогичные (6) нормированные значения этих метрик. В качестве минимальных и максимальных значений мер (7) - (10) следует, очевидно, принять следующие значения:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ; (12)
; (12)
![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; (13)
; (13)
![]() ,
, ![]() .
.
Заметим, что в формуле (12) сумма ![]() представляет собой суммарную сложность всех понятий, входящих в набор
представляет собой суммарную сложность всех понятий, входящих в набор ![]() (исключая понятие
(исключая понятие ![]() ). Аналогично в формуле (13) сумма
). Аналогично в формуле (13) сумма ![]() есть ни что иное, как суммарная важность всех отношений, связывающих между собой понятия набора
есть ни что иное, как суммарная важность всех отношений, связывающих между собой понятия набора ![]() .
.
Аналогично п. 4.1, на основе нормированных метрик ![]() ,
, ![]() легко построить различные M-бальные шкалы оценок, в частности, линейную 5-бальную шкалу, приведенную в таблице 1. По аналогии с п. 4.1 можно предложить значительное количество метрик, которые являются модификациями метрик (7) – (10) (см. Замечание 1).
легко построить различные M-бальные шкалы оценок, в частности, линейную 5-бальную шкалу, приведенную в таблице 1. По аналогии с п. 4.1 можно предложить значительное количество метрик, которые являются модификациями метрик (7) – (10) (см. Замечание 1).
5. Пример
Рассмотрим в качестве примера модуль «Классификация детерминированных задач оптимизации» учебного курса «Методы оптимизации» [8]. В этом модуле дано следующее определение понятия «задача линейного программирования»:
«Если в детерминированной задаче оптимизации критерий оптимальности - линейная функция, а множество допустимых значений вектора варьируемых параметров - выпуклый многогранник, то такая задача называется задачей линейного программирования».
Пусть ![]() есть выходное понятие «задача линейного программирования» рассматриваемого модуля;
есть выходное понятие «задача линейного программирования» рассматриваемого модуля; ![]() ,
, ![]() ,
, ![]() ,
, ![]() - входные понятия «детерминированная задача оптимизации», «критерий оптимальности», «линейная функция», «множество допустимых значений вектора варьируемых параметров», «выпуклый многогранник», соответственно. Нам понадобится далее также понятие
- входные понятия «детерминированная задача оптимизации», «критерий оптимальности», «линейная функция», «множество допустимых значений вектора варьируемых параметров», «выпуклый многогранник», соответственно. Нам понадобится далее также понятие ![]() - «выпуклое множество». Отметим, что входные понятия
- «выпуклое множество». Отметим, что входные понятия ![]() ,
, ![]() ,
, ![]() ,
, ![]() определены в данном курсе, а понятия
определены в данном курсе, а понятия ![]() ,
, ![]() - в других курсах.
- в других курсах.
Понятия ![]() -
- ![]() информационно связанны с понятием
информационно связанны с понятием ![]() в широком смысле, т.е.
в широком смысле, т.е. ![]() и
и ![]() . Вычислительные сложности понятий набора
. Вычислительные сложности понятий набора ![]() образуют совокупность
образуют совокупность ![]() . Положим, что
. Положим, что
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Кроме отношения ![]() «определяемое понятие – определяющие понятие» определим отношение
«определяемое понятие – определяющие понятие» определим отношение ![]() - «разновидность» или «a kind of», а также отношение
- «разновидность» или «a kind of», а также отношение ![]() - «часть целого» или «has a part». В этих обозначениях понятия набора
- «часть целого» или «has a part». В этих обозначениях понятия набора ![]() связаны между собой следующими отношениями: понятия
связаны между собой следующими отношениями: понятия ![]() - отношениями
- отношениями ![]() ; понятия
; понятия ![]() и понятия
и понятия ![]() - отношением
- отношением ![]() ; понятия
; понятия ![]() и понятия
и понятия ![]() - отношениями
- отношениями ![]() . Таким образом,
. Таким образом, ![]() и
и
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
«Важность» отношений ![]() положим равными
положим равными ![]() ,
, ![]() ,
, ![]() , соответственно. Тогда имеем:
, соответственно. Тогда имеем:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Итого, семантическая сеть ![]() понятия
понятия ![]() имеет вид взвешенного ориентированного мультиграфа без контуров
имеет вид взвешенного ориентированного мультиграфа без контуров ![]() (Рис. 1).
(Рис. 1).
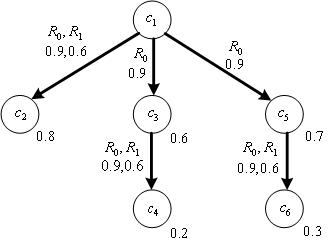
Рис. 1. Мультиграф семантической сети ![]()
Положим, что в набор понятий ![]() , сформированный субъектом обучения, входят правильные понятия
, сформированный субъектом обучения, входят правильные понятия ![]()
![]() ,
, ![]() (понятия из набора
(понятия из набора ![]() ), и неправильное понятие
), и неправильное понятие ![]() (не входящее в набор
(не входящее в набор ![]() ). Другими словами, пусть в когнитивной карте
). Другими словами, пусть в когнитивной карте ![]() заданы понятия
заданы понятия ![]() ,
, ![]() ,
, ![]() ,
, ![]() , так что
, так что ![]() . Множество правильных номеров понятий
. Множество правильных номеров понятий ![]() при этом имеет вид
при этом имеет вид ![]() , а множество неправильных номеров понятий
, а множество неправильных номеров понятий ![]() .
.
Положим также, что субъект обучения задал следующие отношения между указанными понятиями: понятия ![]() - правильные отношения
- правильные отношения ![]() ; понятия
; понятия ![]() - правильное отношение
- правильное отношение ![]() и неправильное отношение
и неправильное отношение ![]() ; понятия
; понятия ![]() - правильное отношение
- правильное отношение ![]() ; понятия
; понятия ![]() - отношения
- отношения ![]() . Это означает, что в когнитивной карте
. Это означает, что в когнитивной карте ![]() определены отношения
определены отношения
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
так что ![]() .
.
Итого, когнитивная карта ![]() , соответствующая семантической сети
, соответствующая семантической сети ![]() , представляется в виде взвешенного ориентированного мультиграфа без контуров
, представляется в виде взвешенного ориентированного мультиграфа без контуров ![]() (Рис. 2).
(Рис. 2).
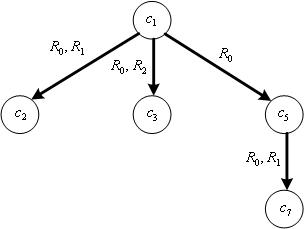
Рис. 2. Мультиграф когнитивной карты ![]()
Используем для примера в качестве метрик качества обучения метрику ![]() при
при ![]() и метрику
и метрику ![]() при
при ![]() .
.
Поскольку значения метрики ![]() вычисляются на основе значений метрики
вычисляются на основе значений метрики ![]() , вычислим прежде значение этой метрики:
, вычислим прежде значение этой метрики: ![]() . Таким образом,
. Таким образом, ![]() .
.
Аналогично для метрики ![]() имеем
имеем ![]() ,
, ![]() .
.
Легко видеть, что ![]() . Поэтому
. Поэтому ![]() ,
, ![]() и
и
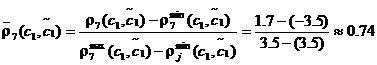 .
.
По линейной 5-бальной шкале (Табл. 1) значению метрики ![]() , равному 1.7, соответствует оценка 4.
, равному 1.7, соответствует оценка 4.
Аналогично для метрики ![]() имеем:
имеем:
![]() ;
;
![]() ,
, ![]() ;
;
![]() .
.
Таким образом, по той же 5-бальной шкале значению метрики ![]() , равному 1.3, также соответствует оценка 4.
, равному 1.3, также соответствует оценка 4.
Заключение
В работе предложена методика контроля понятийных знаний субъекта обучения в обучающей системе, база знаний которой построена на основе семантической сети. Приведена формализация семантической сети. Для формализации представлений субъекта обучения о понятийном составе изучаемой дисциплины предложено использовать когнитивные карты. Качество усвоения субъектом обучения понятия предметной области изучаемой дисциплины оценивается мерой близости графа семантической сети и графа, определяемого соответствующей когнитивной картой. Предложено ряд метрик, формализующих близость указанных графов, как использующих меры сложности понятий и меры важности отношений между ними, так и не использующие их. Рассмотрен конкретный пример, иллюстрирующий предложенную методику.
Литература
1. Калмыков А.А. Системный анализ образовательных технологий. – Пермь: Изд-во Пермского ун-та, 2002
2. Авдеева З.К., Коврига С.В., Макаренко Д.И., Максимов В.И. Когнитивный подход в управлении // Проблемы управления, 2007, ╧3, с. 2-8.
3. Карпенко А.П., Соколов Н.К. Контроль понятийных знаний субъекта обучения с помощью когнитивных карт // Управление качеством инженерного образования и инновационные образовательные технологии. Сборник докладов Международной научно-методической конференции 28-30 октября 2008 г. –М.:МГТУ им. Н.Э.Баумана, 2008, Ч.2, с. 55-57.
4. Овдий О.М., Проскудина Г.Ю. Обзор инструментов инженерии онтологий, http://www.elbib.ru/index.phtml? page=elbib/rus/journal/2004/part4/op
5. Карпенко А.П., Соколов Н.К. Оценка сложности семантической сети в обучающей системе // «Наука и образование: электронное научно-техническое издание», www.technomag.edu.ru, ноябрь, 2008.
6. Карпенко А.П., Соколов Н.К. Расширенная семантическая сеть обучающей системы и оценка ее сложности // «Наука и образование: электронное научно-техническое издание», www.technomag.edu.ru, декабрь, 2008.
7. Норенков И.П., Уваров М.Ю. База и генератор образовательных ресурсов // Информационные технологии, 2005, ╧9, с. 60-65.
8. Карпенко А.П. Методы оптимизации. Учебный курс. //http://bigor.bmstu.ru
Публикации с ключевыми словами: обучающая система, семантическая сеть, контроль понятийных знаний, когнитивная карта
Публикации со словами: обучающая система, семантическая сеть, контроль понятийных знаний, когнитивная карта
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



