научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2008
DOI: 10.7463/1208.0111716
УДК 519.6
А.П.Карпенко, Н.К.Соколов
МГТУ им. Н.Э. Баумана, 105005, Москва, 2-я Бауманская ул., д.5.
Введение
Рассматривается обучающая система, реализующая способ создания учебных материалов на основе «сборки» их из предварительно разработанных модулей или разделяемых единиц контента. Такую технологию поддерживает широко известный стандарт SCORM [1], а также оригинальная отечественная разработка, называемая технологий разделяемых единиц контента [2]. Заметим, что, в отличие от технологии SCORM, технология разделяемых единиц контента обеспечивает взаимосвязь между модулями путем задания отношений «определяемое понятие – определяющее понятие».
Работа является продолжением работы [3], в которой рассматривается база знаний обучающей системы на основе семантической сети, содержащей понятия предметной области изучаемой дисциплины и указанные выше отношения между этими понятиями. В данной работе полагается, что база знаний построена на основе так называемой расширенной семантической сети, которая наряду с отношением «определяемое понятие – определяющее понятие» содержит другие отношения между понятиями, например,
· отношение "часть - целое" (класс - подкласс);
· количественные отношения (больше, меньше, равно);
· пространственные отношения (далеко от, близко от, под, над);
· временные отношения (в течение, позже);
· логические отношения (и, или, не);
· атрибутивные отношения (иметь свойство, иметь значение) и т.д.
Более строго, рассматриваемая в работе семантическая сеть классифицируется как неоднородная (с различными типами отношений между узлами сети) и бинарная (отношения связывают только по два узла сети).
Как и работа [3], данная работа ориентирована на организацию контроля понятийных знаний субъекта обучения в обучающей системе, точнее говоря – на организацию контроля усвоения субъектом обучения понятий предметной области изучаемой дисциплины, а также взаимосвязей этих понятий. Целью работы является конструирование оценок сложности понятий, модулей, репозитариев (библиотек) модулей и обучающих курсов, необходимых для оценки уровня усвоения понятийных знаний. Эти же оценки необходимы для формирования индивидуальной образовательной траектории в интеллектуальной обучающей системе, менеджмента качества учебного процесса, проектирования учебных планов образовательных программ и пр.
Все предложенные в работе меры сложности представляют собой аддитивные свертки соответствующих мер не расширенной семантической сети [3] и мер, которые учитывают специфику расширенной сети. Предложенные меры сложности сконструированы таким образом, что будучи применены к не расширенной семантической сети, дают значения совпадающие со значениями мер, рассмотренными в работе [3].
В разделе 1 вводятся основные обозначения, и приводится постановка задачи. В разделах 2, 3, 4, 5 рассматриваются меры сложности понятий, меры сложности модулей, меры сложности библиотек модулей и меры сложности учебных курсов, соответственно. В заключении сформулированы основные выводы.
1. Модель расширенной семантической сети и постановка задачи
1.1. Модель расширенной семантической сети. Примем следующие обозначения [3].
![]() ,
, ![]() - модуль рассматриваемой библиотеки знаний; M – количество модулей в библиотеке.
- модуль рассматриваемой библиотеки знаний; M – количество модулей в библиотеке.
![]()
![]() - входное понятие модуля
- входное понятие модуля ![]() ;
; ![]() - общее количество входных понятий этого модуля.
- общее количество входных понятий этого модуля.
![]()
![]() - выходное понятие модуля
- выходное понятие модуля ![]() ;
; ![]() - общее количество выходных понятий модуля.
- общее количество выходных понятий модуля.
![]() - совокупность входных понятий модуля
- совокупность входных понятий модуля ![]() , информационно связанных в узком смысле с понятием
, информационно связанных в узком смысле с понятием ![]() .
.
![]() - множество выходных понятий модуля
- множество выходных понятий модуля ![]() , информационно связанных в узком смысле с понятием
, информационно связанных в узком смысле с понятием ![]() .
.
![]()
![]() - множество понятий модуля
- множество понятий модуля ![]() (входных и выходных), информационно связанных в узком смысле с понятием
(входных и выходных), информационно связанных в узком смысле с понятием ![]() .
.
![]() - множество входных и выходных понятий контекста
- множество входных и выходных понятий контекста ![]() , информационно связанных в широком смысле с понятием
, информационно связанных в широком смысле с понятием ![]() .
.
![]() - кратность понятия
- кратность понятия ![]() .
.
![]() - количество внутренних ссылочных понятий модуля
- количество внутренних ссылочных понятий модуля ![]() .
. ![]() - количество внешних ссылочных понятий этого модуля.
- количество внешних ссылочных понятий этого модуля.
![]() - библиотека модулей; M – количество модулей в библиотеке.
- библиотека модулей; M – количество модулей в библиотеке.
![]() - учебный курс, подготовленный из модулей
- учебный курс, подготовленный из модулей ![]() ,
, ![]() ,…,
,…,![]() библиотеки
библиотеки ![]() ;
; ![]() - количество модулей в курсе
- количество модулей в курсе ![]() .
.
![]() ,
, ![]() - совокупность бинарных отношений между понятиями рассматриваемой библиотеки модулей, где
- совокупность бинарных отношений между понятиями рассматриваемой библиотеки модулей, где ![]() - отношение «определяемое понятие – определяющее понятие».
- отношение «определяемое понятие – определяющее понятие».
![]() - общее количество отношений (из числа отношений
- общее количество отношений (из числа отношений ![]() ,
, ![]() ), связывающих между собой понятия
), связывающих между собой понятия ![]() ,
, ![]() .
.
![]() - общее количество отношений, связывающих понятия
- общее количество отношений, связывающих понятия ![]() ,
, ![]() .
.
![]() - общее количество отношений, связывающих понятие
- общее количество отношений, связывающих понятие ![]() со всеми понятиями, принадлежащими множеству понятий
со всеми понятиями, принадлежащими множеству понятий ![]()
![]() .
.
![]() - общее количество отношений, связывающих понятие
- общее количество отношений, связывающих понятие ![]() со всеми понятиями, принадлежащими множеству понятий
со всеми понятиями, принадлежащими множеству понятий ![]() ;
; ![]() .
.
![]() - общее количество отношений, связывающих понятия модуля
- общее количество отношений, связывающих понятия модуля ![]() между собой в контексте
между собой в контексте ![]() .
.
![]() - ориентированный взвешенный граф без контуров, вершины которого соответствуют входным и выходным понятиям модуля
- ориентированный взвешенный граф без контуров, вершины которого соответствуют входным и выходным понятиям модуля ![]() , а дуги отношениям
, а дуги отношениям ![]() «определяемое понятие – определяющее понятие» между ними. Вес дуги, связывающей понятия
«определяемое понятие – определяющее понятие» между ними. Вес дуги, связывающей понятия ![]() ,
, ![]() , равен
, равен ![]() , а вес дуги, связывающей понятия
, а вес дуги, связывающей понятия ![]() ,
, ![]() , равен
, равен ![]() .
.
Замечание. С содержательной точки зрения граф ![]() естественно было бы представлять в виде мультиграфа, в котором дуги, связывающие понятия
естественно было бы представлять в виде мультиграфа, в котором дуги, связывающие понятия ![]() ,
, ![]() соответствуют отношениям
соответствуют отношениям ![]() ,
, ![]() . Однако, с точки зрения целей работы достаточно более простой модели в виде взвешенного графа.
. Однако, с точки зрения целей работы достаточно более простой модели в виде взвешенного графа.
![]()
 - взвешенный понятийный граф библиотеки
- взвешенный понятийный граф библиотеки ![]() (учебного курса
(учебного курса ![]() ), имеющий, возможно, контуры.
), имеющий, возможно, контуры.
![]() (
(![]() ) - граф информационных связей модулей библиотеки L(учебного курса
) - граф информационных связей модулей библиотеки L(учебного курса ![]() ), представляющий собой взвешенный мультиграф и, имеющий, возможно, контуры.
), представляющий собой взвешенный мультиграф и, имеющий, возможно, контуры.
![]() - количество выходных понятий модуля
- количество выходных понятий модуля ![]() , которые используются в качестве входных понятий модуля
, которые используются в качестве входных понятий модуля ![]() в контексте
в контексте ![]() .
.
![]() - общее количество отношений, связывающих между собой модули
- общее количество отношений, связывающих между собой модули ![]() ,
, ![]() в контексте
в контексте ![]() .
.
![]() ,
, ![]() ,
, ![]() - общее количество отношений, связывающих между собой все модули контекста
- общее количество отношений, связывающих между собой все модули контекста ![]() .
.
При графическом изображении графа ![]() ,
, ![]() , вес дуги, связывающей модули
, вес дуги, связывающей модули ![]() ,
, ![]() , определяется величинами
, определяется величинами ![]() ,
, ![]() , которые записываются возле дуги через косую черту.
, которые записываются возле дуги через косую черту.
![]() ,
, ![]() - количества контуров в графах
- количества контуров в графах ![]() ,
, ![]() , соответственно, в контексте
, соответственно, в контексте ![]() .
.
![]() - высоты понятия
- высоты понятия ![]() в контексте
в контексте ![]() .
.
![]() - высота ярусно-параллельной формы графа
- высота ярусно-параллельной формы графа ![]() в контексте
в контексте ![]() .
.
![]() - высоты ярусно-параллельной формы графа
- высоты ярусно-параллельной формы графа ![]() ,
, ![]() .
.
![]() - диаметр графа
- диаметр графа ![]() ,
, ![]() .
.
![]() - реберная плотность графа
- реберная плотность графа ![]() ,
, ![]() .
.
1.2. Постановка задачи. Ставится следующая задача: для расширенной семантической сети сформировать (расширенные) меры сложности понятий ![]() , (расширенные) меры сложности модулей
, (расширенные) меры сложности модулей ![]() , (расширенные) меры сложности библиотек модулей
, (расширенные) меры сложности библиотек модулей ![]() и (расширенные) меры сложности учебных курсов
и (расширенные) меры сложности учебных курсов ![]() , значения которых определяются путем анализа графов
, значения которых определяются путем анализа графов ![]() ;
; ![]() и
и ![]() ;
; ![]() и
и ![]() , соответственно.
, соответственно.
Контекст, в котором рассматриваются расширенные меры сложности понятий, указывается надиндексом, так что мера ![]()
![]() означает сложность понятия
означает сложность понятия ![]() в рамках модуля
в рамках модуля ![]() , мера
, мера ![]() - ту же сложность в рамках библиотеки
- ту же сложность в рамках библиотеки ![]() , мера
, мера ![]() - в пределах курса
- в пределах курса ![]() . Аналогично вводятся расширенные меры сложности модулей
. Аналогично вводятся расширенные меры сложности модулей ![]()
![]() ,
, ![]() ,
, ![]() .
.
Расширенные меры сложности библиотеки ![]() , построенные на основе графов
, построенные на основе графов ![]() ,
, ![]() , обозначаются
, обозначаются ![]() ,
, ![]() , соответственно. Аналогично вводятся расширенные меры сложности
, соответственно. Аналогично вводятся расширенные меры сложности ![]() ,
, ![]() учебного курса
учебного курса ![]() .
.
Расширенная мера сложности понятия ![]() называется контекстно-независимой мерой, если
называется контекстно-независимой мерой, если ![]() =
=![]() =
=![]() , и контекстно-зависимой мерой – если
, и контекстно-зависимой мерой – если ![]()
![]() ,
, ![]()
![]() . Аналогично определяются контекстно-независимая и контекстно-зависимая расширенные меры сложности модуля
. Аналогично определяются контекстно-независимая и контекстно-зависимая расширенные меры сложности модуля ![]() .
.
2. Расширенные меры сложности понятий
1). Контекстно независимая мера ![]() ,
, ![]() представляет собой аддитивную свертку меры сложности
представляет собой аддитивную свертку меры сложности ![]() (взвешенное количество входных и выходных понятий модуля
(взвешенное количество входных и выходных понятий модуля ![]() , информационно связанных с понятием
, информационно связанных с понятием ![]() в узком смысле [3]) и общего количества отношений, связывающих в узком смысле понятие
в узком смысле [3]) и общего количества отношений, связывающих в узком смысле понятие ![]() с другими понятиями модуля
с другими понятиями модуля ![]() :
:
![]()
![]() . (1)
. (1)
Здесь и далее ![]() - весовой множитель.
- весовой множитель.
Рассмотрим для примера модуль ![]() , граф расширенной семантической сети которого
, граф расширенной семантической сети которого ![]() представлен на Рис. 1. Легко видеть, что для понятий этого модуля справедливы следующие оценки:
представлен на Рис. 1. Легко видеть, что для понятий этого модуля справедливы следующие оценки:
![]()
![]() ;
; ![]() ,
, ![]() ;
;
![]()
![]() ,
, ![]() ,
, ![]() .
.

Рис. 1. Пример. Граф ![]() модуля
модуля ![]() расширенной семантической сети.
расширенной семантической сети.
2). Контекстно зависимая мера ![]() - это аддитивная свертка меры сложности
- это аддитивная свертка меры сложности ![]() (высота понятия
(высота понятия ![]() ) и количества отношений, связывающих в широком смысле понятие
) и количества отношений, связывающих в широком смысле понятие ![]() с другими понятиями (в соответствующем контексте):
с другими понятиями (в соответствующем контексте):
![]()
![]() ,
, ![]() . (2)
. (2)
К примеру, для модуля ![]() (см. Рис. 1) имеем:
(см. Рис. 1) имеем:
![]()
![]() ;
; ![]() ,
, ![]() ;
;
![]()
![]() ,
, ![]() ,
, ![]() .
.
3). Контекстно зависимая мера ![]() ,
, ![]() строится на основе меры сложности
строится на основе меры сложности ![]() (суммарное количество понятий, информационно связанных в широком смысле с понятием
(суммарное количество понятий, информационно связанных в широком смысле с понятием ![]() ) и определяется аналогично мере (2). Для модуля
) и определяется аналогично мере (2). Для модуля ![]() (см. Рис. 1), например, имеем следующие оценки:
(см. Рис. 1), например, имеем следующие оценки:
![]()
![]() ;
; ![]() ,
, ![]() ;
;
![]()
![]() ,
, ![]() ,
, ![]() .
.
Отметим, что равенства ![]()
![]() ,
, ![]()
![]() являются случайными. В общем случае такие равенства не имеют место.
являются случайными. В общем случае такие равенства не имеют место.
4). Контекстно зависимая мультимера ![]() является аддитивной сверткой мер
является аддитивной сверткой мер ![]() ,
, ![]() ,
, ![]() , рассматриваемых в соответствующих контекстах:
, рассматриваемых в соответствующих контекстах:
![]() ,
, ![]() .
.
Здесь ![]() - вектор весовых множителей;
- вектор весовых множителей; ![]() ,
, ![]() . Для простоты записи весовые множители в выражениях для
. Для простоты записи весовые множители в выражениях для ![]() -
- ![]() опущены.
опущены.
Вместо количества отношений ![]() в формуле (1) и количества отношений
в формуле (1) и количества отношений ![]() в выражениях для мер
в выражениях для мер ![]() ,
, ![]() могут использоваться их нормированные величины. В качестве нормирующих коэффициентов могут использоваться, например, меры
могут использоваться их нормированные величины. В качестве нормирующих коэффициентов могут использоваться, например, меры ![]() ,
, ![]() .
.
С точки зрения простоты интерпретации и минимума вычислительной сложности, из числа рассмотренных расширенных мер сложности понятий предпочтительными представляются меры ![]() ,
, ![]() .
.
3. Расширенные меры сложности модулей
1). Контекстно независимая мера ![]() ,
, ![]() представляет собой аддитивную свертку меры
представляет собой аддитивную свертку меры ![]() (сумма количеств понятий, связанных в узком смысле с каждым из выходных понятий модуля
(сумма количеств понятий, связанных в узком смысле с каждым из выходных понятий модуля ![]() ) и количества отношений, связывающих все понятия модуля
) и количества отношений, связывающих все понятия модуля ![]() между собой:
между собой:
![]()
![]() . (3)
. (3)
Как и ранее, рассмотрим в качестве примера модуль ![]() (см. Рис. 1). Из п. 2.1) следует, что
(см. Рис. 1). Из п. 2.1) следует, что ![]() ; второе слагаемое в формуле (3), легко видеть, равно 11. Таким образом,
; второе слагаемое в формуле (3), легко видеть, равно 11. Таким образом, ![]() .
.
2). Контекстно зависимая мера ![]() ,
, ![]() является аддитивной сверткой меры
является аддитивной сверткой меры ![]() (сумма высот всех входных и выходных понятий модуля
(сумма высот всех входных и выходных понятий модуля ![]() ) и количества отношений, связывающих все понятия модуля
) и количества отношений, связывающих все понятия модуля ![]() между собой. Мера определяется по формуле, аналогичной формуле (3):
между собой. Мера определяется по формуле, аналогичной формуле (3):
![]()
![]() . (4)
. (4)
Для модуля ![]() (см. Рис. 1) имеем:
(см. Рис. 1) имеем: ![]() (см. п. 2.2));
(см. п. 2.2)); ![]() .
.
3). Контекстно зависимая мера ![]() ,
, ![]() строится на основе меры сложности
строится на основе меры сложности ![]() (сумма количеств понятий, информационно связанных в широком смысле с каждым из выходных понятий модуля
(сумма количеств понятий, информационно связанных в широком смысле с каждым из выходных понятий модуля ![]() ) и определяется аналогично (4).
) и определяется аналогично (4).
К примеру, для модуля ![]() (см. Рис. 1) имеем:
(см. Рис. 1) имеем: ![]() (см. п. 2.3));
(см. п. 2.3)); ![]() .
.
4). Контекстно независимая мера сложности ![]() ,
, ![]() есть ни что иное, как аддитивная свертка меры
есть ни что иное, как аддитивная свертка меры ![]() (взвешенная сумма количеств входных и выходных понятий модуля
(взвешенная сумма количеств входных и выходных понятий модуля ![]() ) и количества отношений, связывающих все понятия модуля
) и количества отношений, связывающих все понятия модуля ![]() между собой. Мера определяется аналогично мере (3).
между собой. Мера определяется аналогично мере (3).
Рассмотрим в качестве примера модуль ![]() (см. Рис. 1). Для этого модуля имеем:
(см. Рис. 1). Для этого модуля имеем: ![]() ;
; ![]() .
.
5). Контекстно-независимая мера ![]() ,
, ![]() конструируется на основе меры сложности
конструируется на основе меры сложности ![]() (взвешенная сумма количеств внешних и внутренних ссылочных понятий, используемых в модуле
(взвешенная сумма количеств внешних и внутренних ссылочных понятий, используемых в модуле ![]() ) и определяется аналогично (3).
) и определяется аналогично (3).
6). Контекстно-независимая мера ![]() ,
, ![]() строится на основе меры
строится на основе меры ![]() (диаметр графа
(диаметр графа ![]() , ответствующего семантической сети модуля
, ответствующего семантической сети модуля ![]() ) и определяется аналогично (3).
) и определяется аналогично (3).
Как и ранее, для примера рассмотрим модуль ![]() (см. Рис. 1). Для этого модуля
(см. Рис. 1). Для этого модуля ![]() . Поэтому
. Поэтому ![]() .
.
7). Контекстно-независимая мера ![]() ,
, ![]() определяется аналогично (3) на основе меры сложности
определяется аналогично (3) на основе меры сложности ![]() (реберная плотность графа
(реберная плотность графа ![]() ).
).
Для модуля ![]() (см. Рис. 1), имеем:
(см. Рис. 1), имеем:
![]() ;
; ![]() .
.
8). Контекстно-зависимая мультимера ![]() представляет собой аддитивную свертку мер
представляет собой аддитивную свертку мер ![]() -
- ![]() , рассматриваемых в контексте
, рассматриваемых в контексте ![]() :
:
 .
.
Здесь для простоты записи опущены весовые множители в выражениях для ![]() -
- ![]() , а вектор весовых множителей
, а вектор весовых множителей ![]() , где
, где ![]() ,
, ![]() .
.
Варианты мер ![]() -
- ![]() можно получить следующим образом:
можно получить следующим образом:
· нормируя тем или иным образом величины ![]() ;
;
· усредняя эти меры, например, по суммарному количеству ![]() входных и выходных понятий модуля;
входных и выходных понятий модуля;
· используя принцип гарантированного результата [7].
Из соображений простоты интерпретации и минимума вычислительной сложности рекомендуется использовать следующие расширенные меры сложности модулей: ![]() ;
; ![]() ,
, ![]() .
.
4. Расширенные меры сложности библиотек модулей
1). Мера ![]() ,
, ![]() строится на основе контекстно-независимой меры сложности модулей
строится на основе контекстно-независимой меры сложности модулей ![]() :
:
![]()
![]() . (5)
. (5)
Здесь ![]() ,
, ![]() .
.
2). Мера сложности ![]() ,
, ![]() формируется на основе контекстно-зависимой меры сложности модулей
формируется на основе контекстно-зависимой меры сложности модулей ![]() по формуле, аналогичной формуле (5):
по формуле, аналогичной формуле (5):
![]()
![]() . (6)
. (6)
3). Мера сложности ![]() ,
, ![]() конструируется на основе контекстно-зависимой меры сложности модулей
конструируется на основе контекстно-зависимой меры сложности модулей ![]() и определяется аналогично (6).
и определяется аналогично (6).
4). Меры сложности ![]() -
- ![]() формируются, соответственно, на основе контекстно-независимых мер сложности модулей
формируются, соответственно, на основе контекстно-независимых мер сложности модулей ![]() -
- ![]() и определяется аналогично мере (5).
и определяется аналогично мере (5).
5). Мера ![]() ,
, ![]() представляет собой аддитивную свертку меры
представляет собой аддитивную свертку меры ![]() (взвешенная сумма количеств вершин и кратностей дуг в графе
(взвешенная сумма количеств вершин и кратностей дуг в графе ![]() ) и общего количества отношений, связывающих в графе
) и общего количества отношений, связывающих в графе ![]() модули библиотеки L между собой:
модули библиотеки L между собой:
![]()
![]() . (7)
. (7)
Рассмотрим в качестве примера библиотеку модулей ![]() , граф
, граф ![]() которой представлен на Рис. 2. Легко видеть, что
которой представлен на Рис. 2. Легко видеть, что ![]() ;
; ![]() ;
; ![]() .
.
6). Меры сложности ![]() ,
, ![]() ,
, ![]() строятся на основе мер сложности библиотеки модулей
строятся на основе мер сложности библиотеки модулей ![]() -
- ![]() , соответственно, и определяются аналогично (7). Напомним, что меры
, соответственно, и определяются аналогично (7). Напомним, что меры ![]() ,
, ![]() ,
, ![]() представляют собой высоту, реберную плотность и количество контуров в графе
представляют собой высоту, реберную плотность и количество контуров в графе ![]() , соответственно, а
, соответственно, а ![]() - общее количество кратных понятий в библиотеке L.
- общее количество кратных понятий в библиотеке L.

Рис. 2. Пример. Граф ![]() библиотеки модулей
библиотеки модулей ![]() расширенной семантической сети.
расширенной семантической сети.
Для библиотеки модулей ![]() (см. Рис. 2) имеем:
(см. Рис. 2) имеем:
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
7). Мультимеры ![]() представляют собой аддитивные свертки мер
представляют собой аддитивные свертки мер ![]() -
- ![]() , соответственно:
, соответственно:
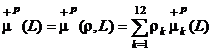 . (8)
. (8)
Здесь для простоты записи опущены весовые множители в выражениях для мер ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; вектор весовых множителей
; вектор весовых множителей ![]() , где
, где ![]() ,
, ![]() ;
;![]() .
.
Легко получить значительное количество вариантов мер ![]() -
- ![]() , используя следующие приемы:
, используя следующие приемы:
· нормировка тем или иным образом величин ![]()
![]() ;
;
· усреднение этих мер, например, по суммарному количеству M модулей в библиотеке;
· конструирование новых мер на основе принцип гарантированного результата [7], среднеквадратичных отклонений ![]() указанных мер от их средних значений, скалярной свертки средних значений мер и их среднеквадратичных отклонений.
указанных мер от их средних значений, скалярной свертки средних значений мер и их среднеквадратичных отклонений.
Из соображений простоты интерпретации и минимума вычислительной сложности рекомендуется использовать расширенные меры сложности библиотек модулей ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() -
- ![]() .
.
5. Расширенные меры сложности учебных курсов
В качестве мер сложности учебного курса ![]() можно использовать меры, аналогичные мерам
можно использовать меры, аналогичные мерам ![]() -
- ![]() библиотеки L. Поскольку корректно построенный учебный курс не должен содержать кратных понятий, меры, аналогичные мере
библиотеки L. Поскольку корректно построенный учебный курс не должен содержать кратных понятий, меры, аналогичные мере ![]() , в этом списке отсутствуют.
, в этом списке отсутствуют.
Таким образом, в качестве мер сложности учебного курса ![]() можно использовать меры
можно использовать меры ![]() -
- ![]() ,
, ![]() . Можно использовать также мультимеру, аналогичную мультмере (8):
. Можно использовать также мультимеру, аналогичную мультмере (8):
 ,
, ![]() .
.
Здесь, как и ранее, для простоты записи опущены весовые множители в выражениях для мер ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; вектор весовых множителей
; вектор весовых множителей ![]() ;
; ![]() ,
, ![]() .
.
Получить варианты мер ![]() -
- ![]() ,
, ![]() можно, используя приемы, приведенные в п. 4 для расширенных мер сложности библиотек модулей.
можно, используя приемы, приведенные в п. 4 для расширенных мер сложности библиотек модулей.
Так же, как для библиотек модулей, рекомендуется использовать следующие расширенные меры сложности учебных курсов: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() -
-![]() .
.
Заключение
Предложенные в работе расширенные меры сложности учебных единиц могут служить также критериями усвояемость соответствующего учебного материала. Особенно естественно использовать в качестве такого критерия меры ![]() ,
, ![]() ,
, ![]() . Аналогично, мера
. Аналогично, мера ![]() может использоваться в качестве критерия гибкости (адаптивности) библиотеки L[3]. Таким образом, рассмотренные в работе расширенные меры сложности позволяют формально ставить задачу оценки качества учебных материалов, как трехкритериальную задачу (с критериями: сложность; усвояемость; адаптивность).
может использоваться в качестве критерия гибкости (адаптивности) библиотеки L[3]. Таким образом, рассмотренные в работе расширенные меры сложности позволяют формально ставить задачу оценки качества учебных материалов, как трехкритериальную задачу (с критериями: сложность; усвояемость; адаптивность).
Авторы благодарят И.П. Норенкова за помощь в формировании концепции работы и множество ценных советов.
Литература
1. Official ADL SCORM overview //http://www.adlnet.gov/scorm
2. Норенков И.П. Технология разделяемых единиц контента для создания и сопровождения информационно-образовательных сред //Информационные технологии, 2003, ╧ 8.
3. Карпенко А.П., Соколов Н.К. Оценка сложности семантической сети в обучающей системе //«Наука и образование: электронное научно-техническое издание», www.technomag.edu.ru, ноябрь, 2008.
4. Карпенко А.П., Федорук В.Г. Обзор программных систем многокритериальной оптимизации. Отечественные системы //Информационные технологии, 2008, ╧1, с. 15-22.
5. Норенков И.П., Уваров М.Ю. База и генератор образовательных ресурсов //Информационные технологии, 2005, ╧9, с. 60-65.
6. Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах. – М.: Университетская книга, Логос, 2006. -292 с.
7. Вентцель Е.С. Исследование операций: задачи, принципы, методология. – М.: Дрофа, 2006. -206 с.
8. Белоус В.В., Васильев Н.В., Карпенко А.П. Вопросы регистрации электронных изданий //Управление качеством инженерного образования и инновационные образовательные технологии. Сборник докладов Международной научно-методической конференции 28-30 октября 2008 г. –М.:МГТУ им. Н.Э.Баумана, 2008, Ч.2, с. 45-50.
9. Полат Е.С., Бухаркина, Моисеева М.В. Теория и практика дистанционного обучения: Учебное пособие для студ. высших педагогических учебных заведений /Под ред. Е.С. Полат. - М.: Издательский центр "Академия", 2004. - 416 с.
Публикации с ключевыми словами: обучающая система, семантическая сеть, разделяемая единица контента, мера сложности
Публикации со словами: обучающая система, семантическая сеть, разделяемая единица контента, мера сложности
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



