научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#10 октябрь 2004
А.А. Березин, канд. биол. наук,
ОИФЗ РАН
Физико-математическая модель нейрона на основе явления возврата Ферми—Паста—Улама для разработки принципиально новых элементов памяти большой емкости
Предлагается новый подход к моделированию нейрона, который интегрируются как распределенная автоволновая система. При этом основным носителем информации в нейроне является спектр возврата Ферми—Паста—Улама нелинейных электроакустических колебаний в молекуле нейронной РНК.
В рамках традиционных представлений электрическая активность отдельного нейрона описывается моделью Ходжкина—Хаксли [1]. При этом в соответствии с формулой Хартли информационная емкость одного нейрона равна log22=1. Другими словами, нейрон рассматривается как система с двумя состояниями и вся сложность информационной работы мозга приписывается наличию большого количества параллельных путей обработки информации. Вместе с тем, в ряде работ [2], [3] сообщается о наличии корреляций между концентрацией рибонуклеиновой кислоты (РНК) и определенных белков в нейронах с процессом обучения животных. Эти данные подтверждают гипотезу о том, что количество РНК в отдельных нейронах может быть связано с их информационной емкостью.
Целью настоящей работы является моделирование процесса функционирования отдельного нейрона головного мозга как элементарной частицы сознания в рамках нелинейной обобщенной квантово - механической модели сознания, предложенной Р. Джаном и Б. Данн [4]. В качестве основного динамического носителя информации предлагается рассмотреть сложный спектр возврата Ферми—Паста—Улама (возврат ФПУ). Как известно из работ по исследованию солитонов [5] возврат ФПУ может быть получен как решение нелинейного уравнения Шредингера (НУШ) с периодическими граничными условиями. Такие решения обладают динамической “памятью” к начальным условиям, что позволяет говорить о возможности использования спектра возврата ФПУ в качестве носителя информации.
Модель электрической активности Нейрона
Рассмотрим нейрон как объем, содержащий сильный электролит внутриклеточной жидкости. Предположим, что все ноны калия в растворе электролита нейтрализованы за счет образования электрически нейтральных пар K+OH- и, как следствие, в растворе наблюдается избыток концентрации протонов. Перечисленные допущения позволяют применить к анализу динамики концентрации протонов кластерную модель электролита морской воды, предложенную Г. Френком и В. Вином [6]. В этой модели каждый ион натрия окружен ионной атмосферой, содержащей четыре молекулы воды, а каждый ион хлора имеет две молекулы воды в своей атмосфере (рис. 1). Рассмотрим в сферическом объеме нейрона одномерную цепочку ионов Na+ и Cl-, расположенную около внутренней поверхности мембраны нейрона, как показано на рис. 1. Процесс деполяризации мембраны порождает концентрационную волну протонов в силу наличия нелинейного механизма перескока протонов между молекулами воды [7]. Электрический потенциал jH образованный совместно ионом натрия и ионной атмосферой иона хлора, может быть записан в рамках теории Дебая—Хюккеля [7] как сумма притягивающей и отталкивающей частей [7].
 (1)
(1)
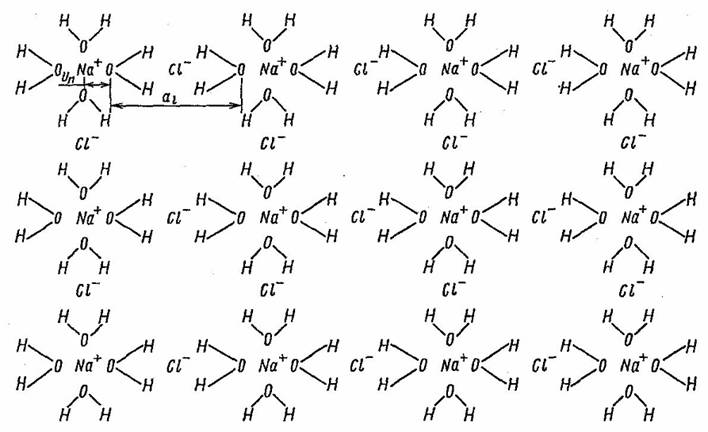
Рис. 1. Ионная структура внутриклеточной жидкости нейрона.
где
 e- заряд электрона
e- заряд электрона
n — концентрация ионов натрия; e — диэлектрическая проницаемость воды; rn — расстояние между ионами натрия и хлора в цепочке, rn=xn-xn-1, где xn — сдвиг n-го протона в цепочке.
С учетом (1) мы можем записать уравнение, описывающее динамику движения протона в цепочке, изображенной на рис. 1, в виде цепочки Тоды [8]:
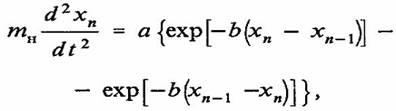 (2)
(2)
где mH — масса протона.
М. Тода показал [8], что уравнение (2) может быть сведено к уравнению Кортевега де Вриза (KdV)
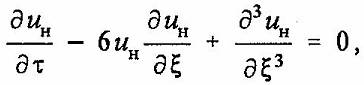 (3)
(3)
где

Сферическая форма нейрона позволяет рассмотреть плоский случай, когда сфера сечется плоскостью. При этом для протонной концентрационной волны, описываемой уравнением (3), периодические граничные условия запишутся в виде:
![]() (4)
(4)
где Ln=2p RH; RH — внутренний радиус нейрона.
Н. Забуски и М. Крускал в своей работе [9] показали, что уравнение (3) вместе с граничными условиями (4) дает решение в виде возврата ФПУ. В предлагаемой модели протонная концентрационная волна в нейроне может быть промодулирована в соответствии с последовательностью нуклеотидов молекулы РНК нейрона (рис. 2). Оценим информационную емкость отдельного нейрона. Принимая во внимание длину перескока протона между молекулами воды, равную 0,86 Å [7], а также температуру электролита внутриклеточной жидкости нейрона T=310K, можно, используя аналогию с плазмой, определить частоту столкновений протонов с молекулами воды:
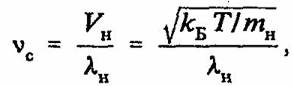 (5)
(5)
где l — свободный пробег протона; VH — скорость протона; mH — масса протона.
Используя длительность нервного импульса, равную нескольким миллисекундам [10] и применяя теорему Котельникова [11], можно формально оценить информационную емкость отдельного спайка:
![]() (6)
(6)
Следующим шагом моделирования является формальное описание высокочастотного информационного сигнала внутри низкочастотной структуры спайка. С этой целью рассмотрим мембрану нейрона в виде жидкого кристалла, содержащего бислой [12] (рис. 2).
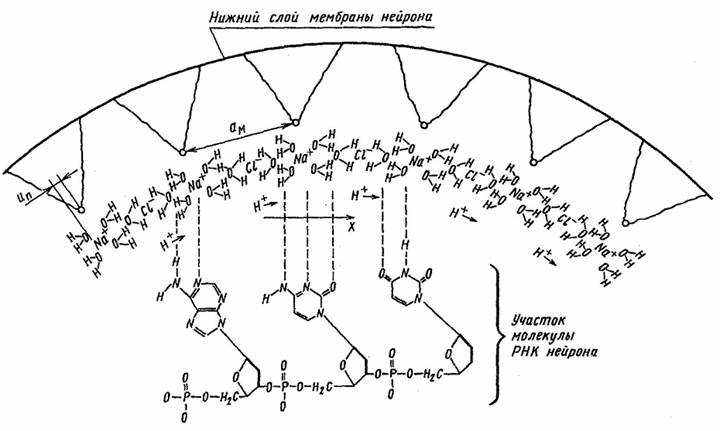
Рис.2 Динамика формирования нового солитона в нейроне
Принимая во внимание, что расстояние между молекулами липидов в мембране, а также расстояние между ионами натрия в электролите составляют порядка 4,7 Å [7], [13], можно предложить следующий механизм взаимодействия высокочастотных протонных концентрационных волн с низкочастотной ионной волной потенциала действия.
Если обозначить Un как расстояние сдвига иона относительно молекулы липида нижнего
бислоя мембраны (рис. 2), то к анализу динамики ионов в нейроне можно применить подход, предложенный Я. Френкелем и Т. Конторовой для описания динамики дислокаций в кристаллах [14]. Обозначим U(Un) как потенциал, действующий на n-й
нон Na+ со стороны неподвижной цепочки липидных молекул в мембране:
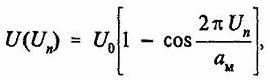 (7)
(7)
где aM — расстояние между двумя соседними липидными молекулами в мембране; U0 относительное положение липидной молекулы. В этих условиях динамика иона Na+ может быть описана следующим уравнением [15]
 (8)
(8)
где mNa – масса иона Na+; p – константа упругости для относительного сдвига ионов Na+.
Переходя в пределе Un(t) ®U(x,t) и вводя функцию, пропорциональную модуляции плотности ионов натрия в виде:
 (9)
(9)
мы получим уравнение синус — Гордона:
 (10)
(10)
где ![]() - скорость продольного звука в
цепочке ионов натрия;
- скорость продольного звука в
цепочке ионов натрия; 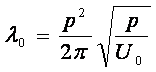 - относительная длина цепочки.
- относительная длина цепочки.
Принимая во внимание, что длина цепочки кратна Ln можно получить солитонное решение уравнения (10) [16] в виде:
 (11)
(11)
где 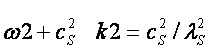 - дисперсионное соотношение.
- дисперсионное соотношение.
Воспользуемся аналогией с экспериментально обнаруженным явлением образования областей пониженной плотности плазмы, которые захватывают ленгмюровские волны [17]. В рамках этого явления можно интерпретировать спайк как низкочастотную уединенную концентрационную волну ионов натрия, в которой захвачена высокочастотная протонная концентрационная волна. Другими словами, спайк может быть описан системой связанных уравнений синус — Гордона и KdV:
 (12)
(12)
где b1<1, b2<1 - коэффициенты взаимодействия между концентрационными волнами ионов натрия и протонными волнами.
В соответствии с результатами работы Г. Икези [17] в которой была использована сходная система уравнений, решение системы (12) представляет солитон с внутренней колебательной структурой. Принимая во внимание результаты работы Н. Забуски и М. Крускала [9] можно записать решение (12) в виде солитона, содержащего спектр ФПУ:
 (13)
(13)
В уравнении (13) функции, отражающие динамику возврата ФПУ в нейроне, выглядят следующим образом:
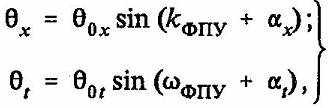 (14)
(14)
где kФПУ - соответственно пространственная и временная частоты возврата ФПУ. Структура спектра ФПУ целиком определяется свойствами нелинейной динамики колебательных процессов в квазипериодическом кристалле молекулы РИК.
Возможная роль РНК как накопителя
информации в нейроне
В ряде своих работ Г. Хиден [18], [20] исследовал корреляцию между процессом обучения у животных и изменениями концентраций РНК и белков в нервных клетках. В результате ему удалось показать, что синтез РНК и белков в нейронах коррелирует с функцией долговременной памяти. В соответствии с гипотезой Г. Хидена объем долговременной памяти отдельного нейрона значительно превышает общепринятые величины. Формальная оценка информационной емкости РНК может быть выполнена следующим образом. Информационная емкость генетического кода составляет log220=4,3 бит на один триплет. Если принять оценку количества цитоплазматической РНК в нейроне, сделанную Г. Хиденом, которая равна 4*1010 дальтон, то количество информации в одном нейроне может достигать 1014 бит.
Вместе с тем молекула РНК может быть интерпретирована как цепочка взаимодействующих квантовых осцилляторов. Каждое звено этой цепочки состоит из фуранозного кольца, связанного с одним азотистым основанием. Рассмотрим упрощенную модель такого звена, в котором осуществлена замена азотистого основания на бензольное кольцо. В соответствии с работой [21] частота квазилокальной вибрационной моды в фуранозном кольце адиабатически зависит от двух конформационных состояний кольца. Предполагая, что оба этих состояния равновероятны, мы можем определить потенциальную энергию делокализованного электрона в фуранозном кольце как симметричную двойную потенциальную яму с двумя минимумами:
![]() (15)
(15)
где ε0 — величина потенциального барьера; Une — смещение электрона относительно вершины барьера; ±U0e — координаты минимумов потенциальной ямы.
Принимая во внимание (15), а также дифференциально-разностную форму уравнения синус — Гордона [22], можно записать уравнение для описания динамики акустической волны в фуранозном кольце в следующей форме:
 (16)
(16)
где φe — амплитуда электронного сдвига в фуранозном кольце; c0 — скорость звука; φ0 — частота, определяемая ε0
Поскольку фуранозное кольцо представляет собой замкнутую дискретную структуру, уравнение (16) может быть дискретизировано, и его решение будет представлять спектр возврата ФПУ [23]. В этом частном случае мы имеем дело с квантовой динамикой возврата ФПУ для энергии фононов акустических волн в фуранозном кольце.
Квантовая динамика бензольного кольца формально представляет систему с двумя состояниями [24]. Однако реальная картина электрического поля в этой молекуле является более сложной. Одним из возможных подходов к его описанию может быть разработан на основе динамики волновых пакетов. Волновые функции с минимальной неопределенностью ΔpΔq представляют собой гауссовы распределения в пространстве координат и в пространстве моментов. Такие функции удобны как основа для построения сложных волновых функций атомов и молекул, поскольку перекрывающиеся интегралы и взаимодействующие матричные элементы могут быть получены алгебраически. В 1975 г. Е. Геллер [25] предложил использовать гауссовы распределения в качестве основы для построения волновых функций. Он предположил, что классическая траектория в фазовом пространстве, в котором гамильтониан в непосредственной близости от движущейся точки pt, qt в данный момент времени t может быть разложен по степеням p - pt, и q - qt до второго порядка как в гармоническом осцилляторе. Волновая функция в этом случае выглядит следующим образом:
![]() (17)
(17)
где α - комплексная симметричная матрица, в которой число колонок и столбцов равно числу степеней свободы; γ — комплексная фаза.
Оценки ожидания для позиции и момента просто равны <p>=pt и <q>=qt; матрица α дает расползание волнового пакета, который соответствует приближенной форме гамильтониана в окрестности (pt, qt). Комплексная фаза γ обеспечивает необходимую нормализацию, а также критический фазовый угол. Временная зависимость параметров α, pt, qt, γ получается путем введения (17) в уравнение Шредингера. Потенциальная энергия раскладывается в ряд до членов второго порядка:
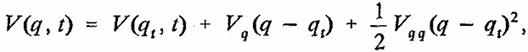 (18)
(18)
где первая и вторая производная Т и 17,,, оцениваются в точке ‚ь во время i.
Основным выводом изложенного подхода является различие спектров гауссовых волновых пакетов в интегрируемой и эргодической областях [26]. Очевидно, что с подобной ситуацией мы сталкиваемся при моделировании динамики молекулы бензола. Линейное уравнение Шредингера в данном случае непригодно. Принимая во внимание подход, предложенный Е. Геллером, а также учитывая малость кинетической энергии по сравнению с энергией покоя электронов в молекуле бензола, мы можем получить нелинейное уравнение Шредингера [27] для описания процесса взаимодействия электронных волновых пакетов в бензольном кольце:
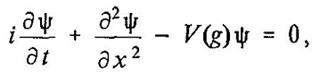 (19)
(19)
где V(g)=ΨΨ* — нелинейный потенциал.
Поскольку бензольное кольцо представляет собой дискретную структуру, можно применить ФПУ - аппроксимацию, используя нелинейное уравнение Шредингера [28]. Следовательно, в молекуле бензола также может существовать квантовый возврат ФПУ.
Для элемента молекулы РНК, состоящего из азотистого основания и фуранозного кольца, динамику взаимодействия электрических волн в бензольном кольце, интерпретирующем азотистое основание, с акустическими волнами в фуранозном кольце можно записать с помощью связанных уравнений синус — Гордона и нелинейного уравнения Шредингера:
 (20)
(20)
где αe>β<1, d=const
Система (20) выглядит как нелинейное обобщение системы Захарова, которая была выведена для описания динамики, электроакустических волн в плазме [29]. В общем случае решение (20) представляет собой стабильный кластер энергии или солитон, имеющий внутреннюю колебательную структуру в виде спектра сложного возврата ФПУ. Связывая элементы (20) молекулы РНК в единую цепь, можно получить макроскопическую цепочку возврата ФПУ для распределения энергии вдоль пространственной координаты в следующем виде:
 (21)
(21)
где α=const; Wn энергия n-го элемента молекулы РНК, определяемого как сумма квадратов амплитуд конечного числа гармоник ФПУ спектра.
Результирующий квазипериодический обмен энергией между различными модами спектра ФПУ в молекуле РНК будет определяться в основном последовательностью нуклеотидов. Любые изменения в молекуле РНК будут играть роль новых граничных условий для спектра возврата ФПУ, осуществляя запись информации в колебательную динамику молекулы. Притом очевидно, что предела количества информации в такой системе не существует. Новая информация приводит лишь к усложнению существующего спектра ФПУ. Нелинейный характер колебаний в молекуле РНК приводит к взаимодействию между микро - и макровозвратами ФПУ. Позже мы оценим порядок основных частот этих Возвратов.
Следующим шагом моделирования является объяснение механизма переноса информации из спектра ФПУ молекулы РНК в структуру спайка. Как было показано в предыдущем параграфе, круговая ионная волна потенциала действия, сформированная в нейроне, также представляет возврат ФПУ. Информация, содержащаяся в спектре возврата ФПУ нейронной РНК, может быть трансформирована через электролит внутриклеточной жидкости нейрона в структуру спайка. Другими словами, любая активация нейрона приводит к передаче в структуру спайка той части информации, которая в данный момент представлена в динамике возврата ФПУ в нейронной РНК.
В связи с очевидной трудностью формализации этого механизма обратимся к его компьютерному и аналоговому моделированию.
Компьютерный эксперимент
Целью компьютерного эксперимента являлось численное исследование решений системы (20). Результаты численного исследования системы Захарова позволили сделать предположение, что решение (20) представляет собой акустический солитон, внутри которого “заперто” высокочастотное электрическое поле. Эта форма решения была экспериментально получена некоторыми исследователями [17] для описания солитонов в плазме.
Система (20) была численно исследована методом Рунге — Кугга. Выбор коэффициентов в уравнениях (20) был продиктован желанием найти устойчивое решение. В результате этой работы были выбраны следующие значения параметров:

Исходное решение показано на рис. 3. На графике вертикальная ось обозначает амплитуды φ,Ψ, а горизонтальная — координату х, t Как видно на графике, решение (20) представляет собой двойной солитон или бризер уравнения синус — Гордона, который включает в себя высокочастотную волну, описываемую с помощью нелинейного уравнения Шредингера. Численный анализ также указывает на наличие квазипериодического возврата во внутренней структуре бризера.
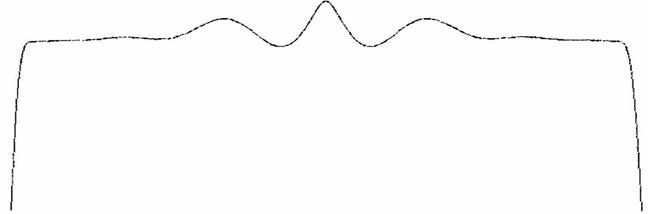
Рис. 3.Компьютерное моделирование решения связанных уравнений синус – Гордона и нелинейного уравнения Шредингера
Очевидность полученного частного случая решения системы (20), а также необходимость оценки эффекта дискретизации уравнений пары (20) привели к постановке аналогового эксперимента.
Аналоговый эксперимент
Эксперимент ставил своей целью осуществить аналоговое исследование модели молекулы РНК, а также смоделировать взаимодействие между спектром колебаний в структуре молекулы РНК и потенциалом действия нейрона. Для этого была сконструирована электрическая модель цепочки РНК в виде двух связанных длинных электрических линий, регенерированных двумя транзисторами. Каждое фуранозное кольцо было представлено двумя нитками, намотанными на пластиковом тороидальном сердечнике. Каждое азотистое основание было также смоделировано в виде двух витков второго трансформатора, намотанного на том же сердечнике. Оба трансформатора состояли из четырех длинных линий по 36 витков каждая, намотанных изолированным проводом диаметром 1 мм на тороидальном пластиковом кольце диаметром 60 мм и толщиной 12 мм.
В предложенной электрической модели каждая первая пара витков служила моделью акустических колебаний в фуранозном кольце. Рассмотрим функцию электронной проводимости в обоих витках. Поскольку токи в них равны по силе и противоположны по направлению, то можно полагать, что все электроны, обеспечивающие проводимость в кристаллической решетке материала витков, являются свободными электронами. Движение электронов в обоих нитках может быть описано двумя аддитивно связанными линейными уравнениями Шредингера [24]:
 (22)
(22)
где Ψ1, Ψ2 — волновые функции электронов в кристаллической решетке проводника первого и второго витка; V(r) — потенциальная энергия электрического поля кристаллической решетки; Е — полная энергия электронов; kп Ψ1(r), kп Ψ2(r) — функции, отражающие взаимодействие волновых функций посредством эффекта Холла; z — период решетки.
В результате того, что направление движения электронов в обоих витках противоположно, решение системы (22) будет выглядеть следующим образом [24]:
 (23)
(23)
где Uk1(r), Uk2(r) — функции Блоха; k1, k2 — усредненные волновые числа электронных волн в обоих витках.
Пространственные биения между электронными волнами в обоих нитках в форме изменения электронной плотности выглядят следующим образом:
 (24)
(24)
Результирующее магнитное поле, образованное биениями, может быть записано в виде:
 (25)
(25)
Изложенный подход позволяет провести аналогию с переходом Джозефсона [30] и описать динамику волн электронной плотности в обоих витках с помощью уравнения синус — Гордона:
 (26)
(26)
где ce – скорость электронного звука в кристаллической решетке проводников; ωe=E/h – электронная частота.
Таким образом, квантовые процессы в фуранозном кольце были смоделированы с помощью динамики электронных волн в каждой паре витков связанных распределенных осцилляторов.
Другая пара витков, принадлежащая второй паре длинных линий, была использована для моделирования динамики электрического поля в азотистом основании. В отличае от предыдущего случая, в этой аналоговой модели обе длинные линии были вкючены согласно, образуя классическую связанную систему из двух линий, в которой имеют место расщепление частот и удвоение положений резонанса [31]. Обе линии включены в коллекторную и эмиттерную цепи транзистора. В этом случае оба транзисторных перехода служат в качестве активных распределенных элементов, имеющих следующую функцию передачи:
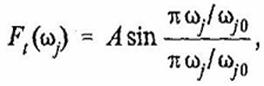 (27)
(27)
где 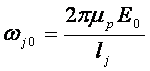 - резонансная частота; μp
– подвижность инжекторных носителей; E0 – напряженность электрического поля, приложенного
к
переходу; lj – длинна перехода; A=const.
- резонансная частота; μp
– подвижность инжекторных носителей; E0 – напряженность электрического поля, приложенного
к
переходу; lj – длинна перехода; A=const.
Резонансные характеристики обоих транзисторных переходов (27) формируют электронные волновые пакеты в каждом витке линии. Расщепление энергитических уровней приводит к модуляции волновых чисел волновых пакетов вокруг своих средних значений. Необходимо отметить, что рассматриваемая модель сходна с парой классических взаимодействующих квантовых осцилляторов, в которых совместная плотность вероятности периодически меняется по времени. Взаимодействие обоих волновых пакетов приводит к взаимной модуляции их волновых чисел, что позволяет воспользоваться нелинейным уравнением Шредингера для описания динамики волновых функций электронов, Ψ3, Ψ4 в каждом витке:
 (28)
(28)
Т. о., взаимодействие между акустическим полем в фуранозном кольце и акустическим полем в азотистом основании может быть записано в виде связанных уравнений синус – Гордона и нелинейного уравнения Шредингера:
 (29)
(29)
Чтобы найти общее резонансное решение уравнений системы (29), используем равенство энергий в обоих парах витков, моделирующих фуранозное кольцо и азотистое основание, также дисперсионное соотношение для акустических и электрических волн:
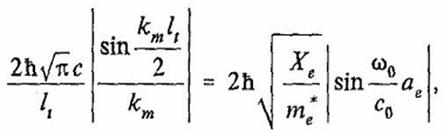 (30)
(30)
где c – скорость света; lt –
длинна витка; Xe – степень обобществления соседних электронов; ![]() - эффективная
масса электрона; ae – расстояние между соседними атомами в
кристаллической решетке материала проводника.
- эффективная
масса электрона; ae – расстояние между соседними атомами в
кристаллической решетке материала проводника.
Типичные значения пространственной km и временной we частот в электронной модели для масштаба размеров кристаллической решетки составляют: km=1,6*103 рад/м, we/(2p)=1016Гц, а для масштаба длинны витков km=4,3 рад/м, we/(2p)=2*106Гц
Учет всей цепочки фуранозных колец и азотистых оснований приводит к необходимости использования уравнения (21), которое описывает квазипериодическое перераспределение энергии или сложный возврат ФПУ. В описанной электронной модели была получена мгновенная картина такого возврата в виде солитона уравнения синус – Гордона, в котором содержится высокочастотный сигнал. Осциллограмма и графическое решение компьютерной модели, качественно совпадают.
Т. о., в рамках предложенной аналоговой модели молекула РНК может быть интерпретирована как носитель сложного возврата ФПУ. Однако, в отличае от классической картины возврата ФПУ, в этой модели спектр возврата ФПУ имеет субструктуру, в которой также наблюдается возврат. Другими словами, микровозврат ФПУ в предложенной модели возникает в результате взаимодействия волновых полей фуранозного кольца и азотистого основания, а микровозврат развивается в модели всей цепочки молекулы РНК.
Следующим шагом моделирования было описание механизма переноса спектра ФПУ из молекулы РНК в структуру спайка. В этих целях электролит внутриклеточной жидкости нейрона был представлен как плотная плазма. Как известно [8], сильный электролит представляет собой промежуточное состояние между хаотическим тепловым движением ионов в растворе и ионной решеткой. Эти свойства позволяют использовать нелинейное уравнение Шредингера и синус – Гордона для моделирования динамики концентрационных волн ионов H+, OH-, Na+, Cl-.
Динамика концентрационных волн ионов Na+ в электролите внутриклеточной жидкости нейрона может быть описана в рамках уравнения синус – Гордона с использованием изложенного выше подхода:
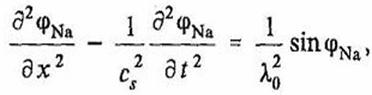 (31)
(31)
где 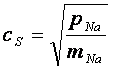 — скорость ионного звука в цепочке
молекул воды; a1 —
расстояние между соседними молекулами воды (см. рис. 1); pNa — упругая константа для относительного сдвига ионов
Na+; l0 —
относительная длина цепочки.
— скорость ионного звука в цепочке
молекул воды; a1 —
расстояние между соседними молекулами воды (см. рис. 1); pNa — упругая константа для относительного сдвига ионов
Na+; l0 —
относительная длина цепочки.
В свою очередь, используя подход В.А.Захарова [32] динамику концентрационных волн ионов в электролите внутриклеточных жидкостей нейрона можно представить с помощью нелинейного уравнения Шредингера (НУШ):
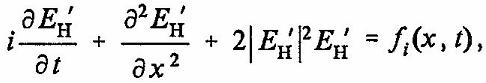 (32)
(32)
где fi(x, t) — случайная функция, разложение Фурье которой имеет характер распределения относительно частоты wi fi(x, t) определяет тепловой шум электролита. В уравнение (31) также должны быть введены члены, отражающие диссипацию и влияние теплового шума электролита:
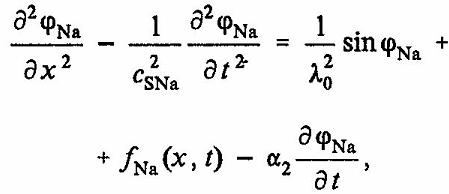 (33)
(33)
где fNa(x, t) — гауссовская случайная функция, определяемая корреляциями [35]
<fi(x, t)>=0
Амплитуда корреляции соотносится с константой b в (34) следующим образом [35]
![]() (34)
(34)
где Т— температура; kБ — константа Больцмана.
Таким образом, взаимодействие концентрационных волн ионов H+, OH-, Na+, Cl-может быть записано в виде связанных уравнений синус — Гордона и НУШ:
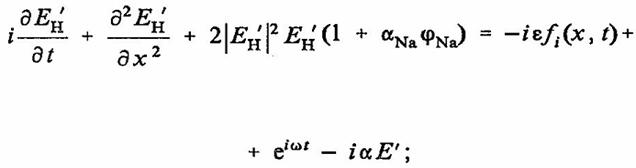 (35)
(35)
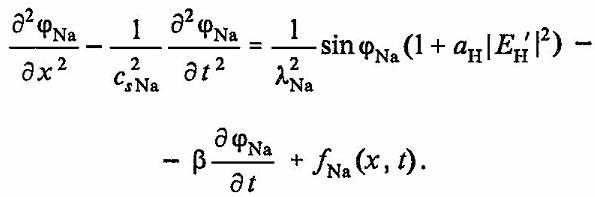 (36)
(36)
Устойчивое решение системы (35) представляет собой солитон уравнения синус — Гордона, содержащий в своей структуре высокочастотные солитоны НУШ. Как показал Б.А. Маломед [35] фундаментальная связь между уравнениями синус — Гордона и НУШ состоит в том, что первое уравнение может рассматриваться как молоамплитудная версия НУШ, что нашло свое проявление в описании ряда физических систем. Кроме того, наличие квазипериодических граничных условий для НУШ в силу периодичности структуры электролита приводит к появлению возврата ФПУ в его решениях [34].
Принимая во внимание результаты изложенного выше моделирования, можно сделать вывод о том, что информационный спектр ФПУ может быть считан с молекулы РНК в нейроне, затем через электролит тканевой жидкости перенесен на мембрану и включен в структуру спайка.
* * *
Резюмируя содержание статьи, можно сделать вывод о том, что нейрон, по-видимому, представляет собой хранилище значительного количества информации, которая содержится в спектре возврата ФПУ электроакустических колебаний в структуре молекулы РНК, а также в растворе электролита внутриклеточной жидкости нейрона. При каждом возбуждении последнего, значительная часть этой информации может быть инкорпорирована во внутреннюю структуру потенциала действия и передана другим нейронам. Поскольку электролит внутриклеточной жидкости, а также плазмы крови представляет собой значительную часть организма, память организма может располагаться не только в нейронах, но и в ионной динамической структуре этих жидкостей. При этом влияние на такую память может осуществляться как электромагнитными, так и электроакустическими внешними полями. В этой связи механизм возникновения предвестников землетрясений в виде изменений поведенческих реакций человека и животных может, по-видимому, быть описан в рамках предлагае мой модели нейрона как элементарной частицы сознания. Помимо этого предложенная модель может быть использована для разработки элементов памяти принципиально нового типа, основанных на квантово механических свойствах распределенных микроосцилляторов.
Список литературы
1. Hodkin A. L., Huxle A. F. // J. Physical (Lond). V. 117. 1952. P. 500.
2. Hyden. H., Egyhazi E. // Proc. Nat. Acad. Sci. USA, V. 52. 1964. P. 1030.
3. Hyden. H. //Human Mind, Amsterdam, 29 (1967).
4. Jahn R. J. and Dunne B. J. // Foundations of Physics. V. 16. N 8. 1986.
5. Юэн Т. и Лейк Б. Теория нелинейных волн на глубокой воде // Солитоны в действии. М.: Мир, 1981ю
6. Frank H. S. and Wen W. Y. // Disc. Faraday Soc. V. 24. 1957. P. 133.
7. Скорчелетти В. В. Теоретическая электрохимия. Л.: Госхимиздат. 1963.
8. Toda M. // Phys. Soc. Japan. V. 22, 431 (1967); ibid, 23, 501, 1967; 26, 235 (1969); 34, 18 (1973); Phys. Reports, 10, 1 (1975)
9. Damask A. C. // Medical physics. V. 1. Academic Press, 1978.
10. Гоноровский И. С. Электронные цепи и сигналы. Т. 1. М.: Сов. Радио, 1967.
11. Америк Ю. Б., Кренцель Б. А. Химия жидких кристаллов и мезаморфных полимерных систем. М.: Наука. 1980.
12. Френкель Я. И., Конторова Т. А. К теории пластической деформации и двойникования // ЖЭТФ, 1938, №8, С. 89.
13. Давыдов А. С. Солитоны в молекулярных структурах. Киев: Наука думка. 1988
14. Пелиновский Е. Н. Некоторые точные методы в теории нелинейных волн // Радиофизика. Т. XIX, №5, 1976. С. 883.
15. Петвиашвилли В. И., Похотелов О. А. Уединенные волны в плазме и атмосфере. М.: Атомиздат. 1989.
16. Parmentier R. D. Fluxons In Distributed Josephson Contacts. Ref 27
17. Калинин В. И., Герштейн Г. М. Введение в радиофизику. М.: ГИТЛ, 1957.
18. Захаров В. Е. Коллапс ленгмюровских волн. // ЖЭТФ. Т. 62. 1972. С 17-45.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, №5. 1997
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



