научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2012
УДК 621.396.4
МГТУ им. Н.Э. Баумана
В настоящее время технология многостанционного доступа с кодовым разделением каналов (CDMA), признана наиболее перспективной для использования в будущих поколениях сетей мобильной связи. Эта технология основана на расширении спектра за счет использования псевдослучайных последовательностей (ПСП). Расширение спектра производится путем модуляции несущего колебания по закону псевдослучайной последовательности. При этом используют либо прямой метод модуляции (системы DS-CDMA), либо модуляцию скачкообразным переключением частоты (FH-CDMA).
Известно достаточно много ансамблей бинарных ПСП, используемых при построении систем связи – последовательности максимальной длины регистра сдвига (М- последовательности), последовательности Голда, Касами, ,Камалетдинова, Баркера, Лежандра, Гордона-Милза-Уэлча (GMW) и др.[1].
Разделение каналов в системе с CDMA осуществляется за счет присвоения каждому абонентскому каналу кодовой ПСП, корреляция которой с последовательностями других каналов минимальна. Центральный пик автокорреляционной функции (АКФ) кодовых последовательностей, используемых в асинхронных системах связи должен существенно превышать боковые лепестки АКФ, а максимальные выбросы взаимно-корреляционных функций (ВКФ) этих последовательностей при всех сдвигах должны быть по возможности минимальны. Для синхронных систем требования к ВКФ не такие жесткие – достаточно обеспечить малую взаимную корреляцию последовательностей в одной точке. Очевидно, что чем более представительный ансамбль последовательностей с минимальной взаимной корреляцией тем больше может быть абонентов в системе. Важным требованием, предъявляемым к современным системам с CDMA, является обеспечение конфиденциальности передачи. С этой целью необходимо.применять ПСП с большим периодом и высоким показателем неопределенности, т.е. с большой линейной сложностью [2].
Широко используемые в настоящее время М-последовательности, коды Голда и Касами поддаются легкой расшифровке. Этого недостатка лишены последовательности, функция формирования которых нелинейна, в частности, последовательности, предложенные Гордоном, Милзом и Уэлчем (GMW).[1] Несомненными их достоинствами являются представительный ансамбль, при больших длинах значительно превосходящий ансамбль М-последовательностей, и достаточно хорошие корреляционные свойства. Однако свойства ансамблей последовательностей GMW, ввиду сложности их формирования, изучены еще недостаточно, методы практической генерации исследованы также мало.
Известные способы генерации GMWпоследовательностей основаны на том, что любую М-последовательность длины 2N-1, где N=mk, т≥2,k≥3, можно представить в виде двумерной матрицы из z=2k-1 столбцов и v=(2n-1)/zстрок. При этом каждая строка является либо некоторым сдвигом более короткой М-последовательности длины 2k-1, либо строкой из одних нулей. Это свойство получило название декомпозиционного свойства М-последовательности, а матрица – декомпозиционной матрицы [3]. Для построения последовательностей GMW длины 2N-1(N=mk, т≥2,k≥3) вдекомпозиционной матрице М-последовательности с параметрами zи vнеобходимо все ненулевые строки, являющиеся сдвигами некоторой более короткой М-последовательности длины z,заменить на строки с теми же сдвигами, но уже другой М-последовательности длины z, не являющейся сдвигом заменяемой М-последовательности. Общее число получаемых GMW-последовательностей при разложении N=тkбудет равно числу различных базисных последовательностей [4].
Все описанные в литературе способы формирования GMW последовательностей основаны на принципе декомпозиции и отличаются только сложностью реализации. Для получения конкретных образцов последовательностей, которые могут быть полезны при исследовании возможностей практического применения в системах с CDMA, а также их изучения были составлены алгоритм и программа. Структурная схема алгоритма представлена на рисунке 1
Последовательность GMW периода L=2N-1 гдеN=mk, т≥2,k≥3 формируется путем декомпозиции Pсимволов различных сдвигов базисной М-последовательности периода L1=2k-1, где P выбирается из условия P=(L+1)/(L1+1), S=L/L1, P<S, и (S–P) символов нуль-последовательностей, состоящих из L1 нулей. При этом каждый сдвиг М-последовательности является целым числом (0, L1), которое берут из декомпозиционного правила Ip.
Для реализации алгоритма была выбрана среда C++Builder 2009, заданы переменные начальные условия и две функции – сдвига строки и собственно реализации алгоритма. Программное воплощение полностью соответствует структурной схеме, приведенной на рис. 1.
Для получения последовательностей GMW достаточно задать базисную М-последовательность и правило декомпозиции – строку чисел длины L1+1со значениями от 0 до L1-1.
Полученные результаты приведены в таблице 1. Из-за сложности получения декомпозиционных правил и для наглядности был выбран ансамбль GMW последовательностей длиной L= 63символа.
Существуют две базисных М-последовательностей длины 7, каждая из них порождает полуансамбль ПСП GMW периода 63.
Для исследования корреляционных свойств полученного ансамбля GMW последовательностей (Таблица 1) была составлена программа и вычислены периодические автокорреляционные функции (ПАКФ ) и апериодические автокорреляционные функции (ААКФ) каждой ПСП из ансамбля, периодические взаимокорреляционные функции (ПВКФ) и апериодические взаимокорреляционные функции (АВКФ) для всех возможных пар ПСП для каждого из двух полуансамблей, а также ПВКФ и АВКФ для пар ПСП, принадлежащих разным полуансамблям, т.е. полученным на основе различных базисных ПСП.
Результаты подтвердили правильность составленной программы и алгоритма:
1) В каждом полуансамбле выделены 3 базовые последовательности. Все остальные ПСП из полуансамбля являются последовательными сдвигами базовых на период кратный 9-ти символам (Таблицы 2 и 3). Например, последовательность 14 является циклическим сдвигом последовательности 4 на 36 символов. Таким образом, существует только 6 образцов полностью уникальных последовательностей GMW периода 63 (Таблица 4).
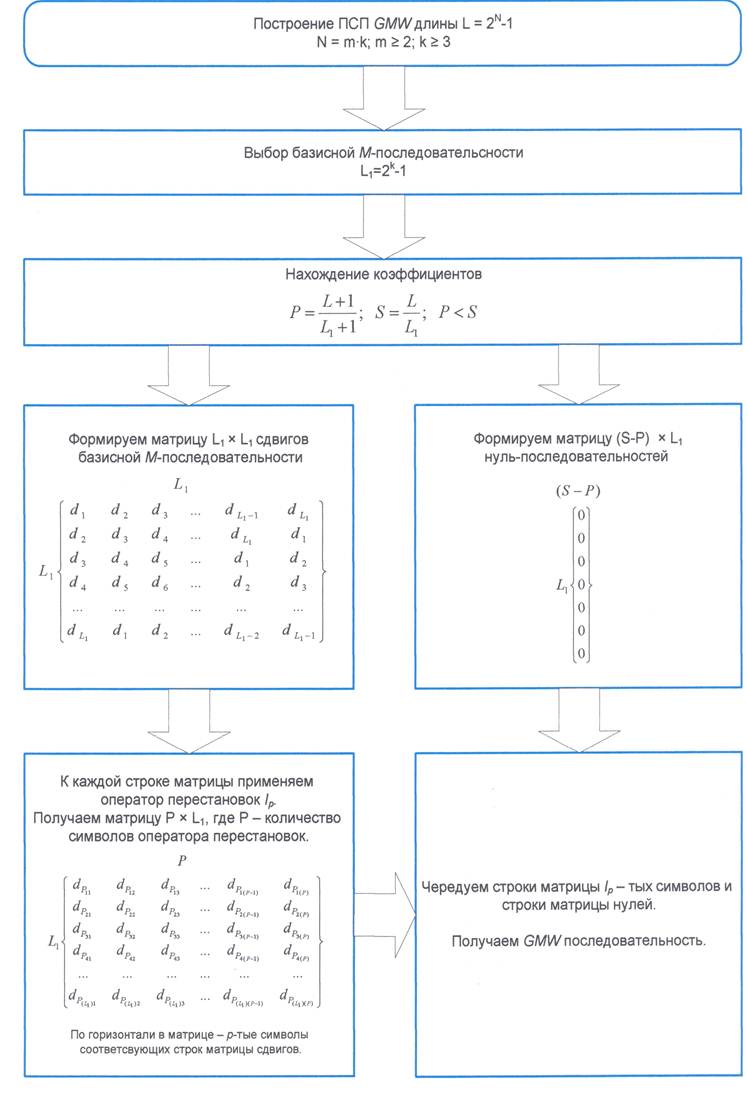
Рис. 1. Структурная схема алгоритма формирования GMWпоследовательностей
Таблица1
Образцы GMW последовательностей
№ | Последовательности GMW | Правило декомпозиции | Базисная М-последовательность | ||||
1 | 2 | 3 | 4 | ||||
1 | 111011110110110110100011110011000000101110110001101000010101000 | 01430200 | 1110100 | ||||
2 | 101100110101100010111011010010111100111011110000000100010111000 | 05015540 | 1110100 | ||||
3 | 100111010111010010111000110011111100100101110011101000000010100 | 06641450 | 1110100 | ||||
4 | 111010010111000110011111100100101110011101000000010100100111010 | 10052561 | 1110100 | ||||
5 | 110110110100011110011000000101110110001101000010101000111011110 | 12541311 | 1110100 | ||||
6 | 101100010111011010010111100111011110000000100010111000101100110 | 16126651 | 1110100 | ||||
7 | 111011010010111100111011110000000100010111000101100110101100010 | 20230062 | 1110100 | ||||
8 | 111000110011111100100101110011101000000010100100111010111010010 | 21163602 | 1110100 | ||||
9 | 100011110011000000101110110001101000010101000111011110110110110 | 23652422 | 1110100 | ||||
10 | 010111100111011110000000100010111000101100110101100010111011010 | 31341103 | 1110100 | ||||
11 | 011111100100101110011101000000010100100111010111010010111000110 | 32204013 | 1110100 | ||||
12 | 011000000101110110001101000010101000111011110110110110100011110 | 34063533 | 1110100 | ||||
13 | 111011110000000100010111000101100110101100010111011010010111100 | 42452214 | 1110100 | ||||
14 | 100101110011101000000010100100111010111010010111000110011111100 | 43315124 | 1110100 | ||||
15 | 101110110001101000010101000111011110110110110100011110011000000 | 45104644 | 1110100 | ||||
16 | 000000100010111000101100110101100010111011010010111100111011110 | 53563325 | 1110100 | ||||
17 | 011101000000010100100111010111010010111000110011111100100101110 | 54426235 | 1110100 | ||||
18 | 001101000010101000111011110110110110100011110011000000101110110 | 56215055 | 1110100 | ||||
19 | 010101000111011110110110110100011110011000000101110110001101000 | 60326166 | 1110100 | ||||
20 | 010111000101100110101100010111011010010111100111011110000000100 | 64604436 | 1110100 | ||||
21 | 000010100100111010111010010111000110011111100100101110011101000 | 65530346 | 1110100 | ||||
1 | 2 | 3 |
| ||||
1’ | 111101110001010100001011000110111010000001100111100010110110110 | 00504360 | 1001011 | ||||
2’ | 101110010010100000001011100111010010011111100110001110100101110 | 02363110 | 1001011 | ||||
3’ | 110011010001110100010000000111101110011110100101101110100011010 | 03226020 | 1001011 | ||||
4’ | 001010100001011000110111010000001100111100010110110110111101110 | 11615401 | 1001011 | ||||
5’ | 010100000001011100111010010011111100110001110100101110101110010 | 13404221 | 1001011 | ||||
6’ | 001110100010000000111101110011110100101101110100011010110011010 | 14330131 | 1001011 | ||||
7’ | 001011000110111010000001100111100010110110110111101110001010100 | 22026512 | 1001011 | ||||
8’ | 001011100111010010011111100110001110100101110101110010010100000 | 24515332 | 1001011 | ||||
9’ | 010000000111101110011110100101101110100011010110011010001110100 | 25441242 | 1001011 | ||||
10’ | 110111010000001100111100010110110110111101110001010100001011000 | 33130623 | 1001011 | ||||
11’ | 111010010011111100110001110100101110101110010010100000001011100 | 35626443 | 1001011 | ||||
12’ | 11110111001И10100101101110100011010110011010001110100010000000 | 36552353 | 1001011 | ||||
13’ | 011110100101101110100011010110011010001110100010000000111101110 | 40663464 | 1001011 | ||||
14’ | 000001100111100010110110110111101110001010100001011000110111010 | 44241034 | 1001011 | ||||
15’ | 011111100110001110100101110101110010010100000001011100111010010 | 46030554 | 1001011 | ||||
16’ | 110001110100101110101110010010100000001011100111010010011111100 | 50141665 | 1001011 | ||||
17’ | 101101110100011010110011010001110100010000000111101110011110100 | 51004505 | 1001011 | ||||
18’ | 111100010110110110111101110001010100001011000110111010000001100 | 55352145 | 1001011 | ||||
19’ | 100101110101110010010100000001011100111010010011111100110001110 | 61252006 | 1001011 | ||||
20’ | 100011010110011010001110100010000000111101110011110100101101110 | 62115616 | 1001011 | ||||
21’ | 110110110111101110001010100001011000110111010000001100111100010 | 66463256 | 1001011 | ||||
Таблица 2
Последовательности GMW на основе базисной М последовательности 1110100
№ | Последовательности GMW | Правило декомпозиции |
1 | 111011110110110110100011110011000000101110110001101000010101000 | 01430200 |
2 | 101100110101100010111011010010111100111011110000000100010111000 | 05015540 |
3 | 100111010111010010111000110011111100100101110011101000000010100 | 06641450 |
4 | 111010010111000110011111100100101110011101000000010100100111010 | 10052561 |
5 | 110110110100011110011000000101110110001101000010101000111011110 | 12541311 |
6 | 101100010111011010010111100111011110000000100010111000101100110 | 16126651 |
7 | 111011010010111100111011110000000100010111000101100110101100010 | 20230062 |
8 | 111000110011111100100101110011101000000010100100111010111010010 | 21163602 |
9 | 100011110011000000101110110001101000010101000111011110110110110 | 23652422 |
10 | 010111100111011110000000100010111000101100110101100010111011010 | 31341103 |
11 | 011111100100101110011101000000010100100111010111010010111000110 | 32204013 |
12 | 011000000101110110001101000010101000111011110110110110100011110 | 34063533 |
13 | 111011110000000100010111000101100110101100010111011010010111100 | 42452214 |
14 | 100101110011101000000010100100111010111010010111000110011111100 | 43315124 |
15 | 101110110001101000010101000111011110110110110100011110011000000 | 45104644 |
16 | 000000100010111000101100110101100010111011010010111100111011110 | 53563325 |
17 | 011101000000010100100111010111010010111000110011111100100101110 | 54426235 |
18 | 001101000010101000111011110110110110100011110011000000101110110 | 56215055 |
19 | 010101000111011110110110110100011110011000000101110110001101000 | 60326166 |
20 | 010111000101100110101100010111011010010111100111011110000000100 | 64604436 |
21 | 000010100100111010111010010111000110011111100100101110011101000 | 65530346 |
Таблица 3
Последовательности GMW на основе базисной М последовательности 1001011
№ | Последовательности GMW | ППравило декомпозиции |
1 | 111101110001010100001011000110111010000001100111100010110110110 | 00504360 |
2 | 101110010010100000001011100111010010011111100110001110100101110 | 02363110 |
3 | 110011010001110100010000000111101110011110100101101110100011010 | 03226020 |
4 | 001010100001011000110111010000001100111100010110110110111101110 | 11615401 |
5 | 010100000001011100111010010011111100110001110100101110101110010 | 13404221 |
6 | 001110100010000000111101110011110100101101110100011010110011010 | 14330131 |
7 | 001011000110111010000001100111100010110110110111101110001010100 | 22026512 |
8 | 001011100111010010011111100110001110100101110101110010010100000 | 24515332 |
9 | 010000000111101110011110100101101110100011010110011010001110100 | 25441242 |
10 | 110111010000001100111100010110110110111101110001010100001011000 | 33130623 |
11 | 111010010011111100110001110100101110101110010010100000001011100 | 35626443 |
12 | 111101110011110100101101110100011010110011010001110100010000000 | 36552353 |
13 | 011110100101101110100011010110011010001110100010000000111101110 | 40663464 |
14 | 000001100111100010110110110111101110001010100001011000110111010 | 44241034 |
15 | 011111100110001110100101110101110010010100000001011100111010010 | 46030554 |
16 | 110001110100101110101110010010100000001011100111010010011111100 | 50141665 |
17 | 101101110100011010110011010001110100010000000111101110011110100 | 51004505 |
18 | 111100010110110110111101110001010100001011000110111010000001100 | 55352145 |
19 | 100101110101110010010100000001011100111010010011111100110001110 | 61252006 |
20 | 100011010110011010001110100010000000111101110011110100101101110 | 62115616 |
21 | 110110110111101110001010100001011000110111010000001100111100010 | 66463256 |
Таблица 4
Последовательности GMW и максимальный уровень боковых лепестков их ААКФ
№ | Последовательности GMW | Правило декомпозиции | Максимальный уровень боковых лепестков ААКФ |
Базисная последовательность - М - последовательность 1110100
|
| ||
1 | 111011110110110110100011110011000000101110110001101000010101000 | 01430200 | 7 |
2 | 101100110101100010111011010010111100111011110000000100010111000 | 05015540 | 7 |
3 | 100111010111010010111000110011111100100101110011101000000010100 | 06641450 | 7 |
Базисная последовательность - М -последовательность 1001011
|
| ||
4 | 111101110001010100001011000110111010000001100111100010110110110 | 00504360 | 9 |
5 | 101110010010100000001011100111010010011111100110001110100101110 | 02363110 | 8 |
6 | 110011010001110100010000000111101110011110100101101110100011010 | 03226020 | 9 |
2) ПАКФ базовых последовательностей из таблицы 4 являются такими же, как у М–последовательностей [5].
3) Максимальный уровень боковых лепестков ААКФ последовательностей GMW соизмерим с максимальным уровнем для М-последовательностей.
4) Максимальные выбросы ПВКФ возможных комбинаций пар последовательностей GMW также не превышают уровня максимальных выбросов ПВКФ М-последовательностей.
5) Максимальные выбросы ПВКФ между любыми парами GMW и М-последовательностей не превышают уровней ПВКФ для М-последовательностей
Заключение
Предложенные в статье алгоритм и программа формирования последовательностей могут быть полезны при исследовании свойств класса нелинейных последовательностей GMW для перспективных систем с кодовым разделением каналов.
Список литературы
1. Golomb S.W., Gong. G. Signal Design for Good Correlation for Wireless Communication, Criptography and Radar . Cambridge University Press , 2005.- 438 P.
2. Системы сотовой и спутниковой связи / В.В.Калмыков, И.Б.Федоров, С.С.Юдачев. Изд.-во «Рудомино», 2010. 280 с.
3. Стельмашенко Б.Г., Тараненко П..Г. Нелинейные псевдослучайные последовательности в широкополосных системах передачи информации. - Зарубежная радиоэлектроника 1988. №9. С. 76-82.
4. Мешковский К.А., Кренгель Е.И. Генерация псевдослучайных последовательностей Гордона, Милза, Велча.. Радиотехника.1998.№5. С. 25-28.
5. Шумоподобные сигналы в системах передачи информации / В.Б.Пестряков, В.П. Афанасьев, В.Л.Гурвиц и др. ; Под. ред. В.Б.Пестрякова. Сов. Радио, 1973. 424 с.
Публикации с ключевыми словами: псевдослучайные последовательности, корреляционные свойства, многостанционный доступ
Публикации со словами: псевдослучайные последовательности, корреляционные свойства, многостанционный доступ
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



