научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2011
УДК 517.984.54
МГТУ им. Н.Э. Баумана
Введение
Обработка результатов измерений является одной из ключевых задач построения фурье-спектрорадиометрических систем (ФСРС) и подразумевает разработку алгоритмов, позволяющих как выполнять преобразование регистрируемой информации в форму спектральных данных, так и интерпретировать спектральную информацию. Последнее требование подразумевает выполнение требования устойчивости получаемого приближенного решения для концентраций веществ в смысле численных методов [1]. Зарекомендовавшим себя методом анализа и интерпретации спектров, является регрессионный анализ нормированного спектра целевых вещества в атмосфере [2, 3]. Для расчета нормированного спектра регистрируются два спектра: суммарный спектр трассы наблюдения при ожидаемом присутствии целевого вещества и спектр подстилающей поверхности без наличия целевых веществ на линии обзора. Однако в ряде случаев принципиально невозможно регистрировать фоновый спектр трассы наблюдения, и необходимо проведение газоанализа в открытой атмосфере по единичному зарегистрированному спектру [3]. В [4] описана методика идентификации и восстановления концентраций веществ по единичному спектру, полученному по пассивной методике регистрации на ФСРС.
В основе интерпретации единичного спектра лежит линейная слоевая модель переноса излучения, позволяющая свести задачу восстановления концентраций к системе линейных алгебраических уравнений (СЛАУ). Данная задача является некорректно поставленной, а матрица системы в ряде случаев может быть плохо обусловленной. В данной статье предлагаются численные процедуры, позволяющие на основе предварительного моделирования спектра атмосферной трассы исключить из рассмотрения атмосферные составляющие. Затем на основе подходов корреляционного анализа многомерная СЛАУ заменяется одной или несколькими одномерными задачами, для которых выполнены все условия корректности.
В настоящей работе исследовано влияние малых шумов во входной информации на решение задачи, определены уровни ошибок в решении обратной задачи для характерных шумов во входных спектрах.
Постановка задачи
В настоящей работе предлагается подход к решению задачи идентификации веществ и определения их концентраций (не являющихся непосредственно наблюдаемыми величинами) по свойствам их спектров, которые наблюдаются непосредственно и напрямую зависят как от искомых величин, так и от внешних факторов.
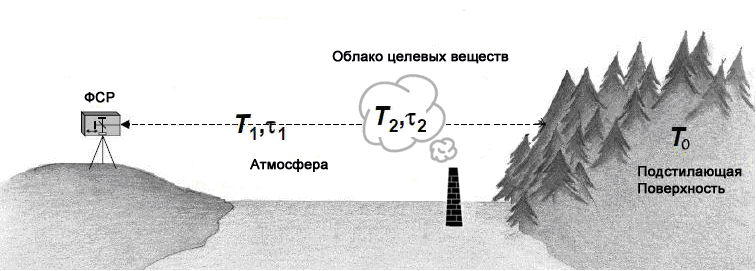
Рис. 1. Упрощенная физическая модель методики беспробоотборного мониторинга веществ в открытой атмосфере
Фурье-спектрорадиометр (ФСР) регистрирует собственное тепловое излучение всех объектов (атмосфера, целевые вещества, подстилающая поверхности) на линии обзора. Считаем, что температуры газовых компонентов на протяженности трассы наблюдения постоянны, что оправдано для приземных трасс наблюдений, где температурные перепады вдоль трассы не превышают нескольких градусов. Если данное требование не выполнено, то считаем, что газовая составляющая излучает при некоторой эффективной температуре. Считаем, что подстилающая поверхность излучает как абсолютно черное тело, что оправдано для большинства как естественных, так и искусственных поверхностей. Рассеянием излучения пренебрегаем. В [4] показано, что в данном случае нормированный спектр газовой составляющей запишется в виде:
| (1) |
где ![]() – нормированный на единицу коэффициент пропускания, содержащий в себе сигнатуры всех объектов и веществ на линии наблюдения ФСР;
– нормированный на единицу коэффициент пропускания, содержащий в себе сигнатуры всех объектов и веществ на линии наблюдения ФСР; ![]() – спектр, регистрируемый в эксперименте;
– спектр, регистрируемый в эксперименте; ![]() – функция Планка;
– функция Планка; ![]() – эффективная температура газовой составляющей трассы наблюдения;
– эффективная температура газовой составляющей трассы наблюдения; ![]() – эффективная температура подстилающей поверхности;
– эффективная температура подстилающей поверхности; ![]() – оптическая плотность трассы наблюдения.
– оптическая плотность трассы наблюдения.
Для смеси невзаимодействующих газов (отсутствие ассоциации, диссоциации и иного химического взаимодействия) оптическая плотность – аддитивная величина [2], поэтому уравнение (1) можно переписать в виде СЛАУ:
| (2) |
где ki(n) – спектральный коэффициент экстинкции данного вещества;![]() – интегральные концентрации веществ находящихся на линии обзора. В матричном виде уравнение (2) можно записать следующим образом:
– интегральные концентрации веществ находящихся на линии обзора. В матричном виде уравнение (2) можно записать следующим образом:
| (3) |
где ![]() – матрица референтных спектров веществ (I – количество референтных спектров веществ, входящих в газовую смесь; J – размер спектра по волновым числам);
– матрица референтных спектров веществ (I – количество референтных спектров веществ, входящих в газовую смесь; J – размер спектра по волновым числам); ![]() – массив (вектор) искомых интегральных концентраций (которые из физических соображений должны быть положительны и не превышать концентрации насыщения
– массив (вектор) искомых интегральных концентраций (которые из физических соображений должны быть положительны и не превышать концентрации насыщения ![]() );
); ![]() – вектор значений оптической плотности трассы наблюдения, содержащий ошибки измерения. Значения kij, составляющие матрицу K, как правило, определяются в лабораторных экспериментах, и поэтому также содержат ошибки измерения.
– вектор значений оптической плотности трассы наблюдения, содержащий ошибки измерения. Значения kij, составляющие матрицу K, как правило, определяются в лабораторных экспериментах, и поэтому также содержат ошибки измерения.
Задачи подобного рода относятся к классу так называемых обратных задач [1], т.е. задач, где необходимо определение интересующих нас количественных характеристик явления по результатам измерений их косвенных проявлений. Поскольку матрица K системы и правая часть ![]() содержат погрешности измерений, то система вида (3) почти всегда несовместна. В этом случае рассматривается решение методом наименьших квадратов:
содержат погрешности измерений, то система вида (3) почти всегда несовместна. В этом случае рассматривается решение методом наименьших квадратов:
| (4) |
которое, во-первых, может не принадлежать множеству определения искомых переменных ![]() , а, во-вторых, в ряде случаев, может быть неустойчиво в асимптотическом смысле. Более того, если даже формально решение устойчиво, но норма матрицы
, а, во-вторых, в ряде случаев, может быть неустойчиво в асимптотическом смысле. Более того, если даже формально решение устойчиво, но норма матрицы ![]() может быть очень мала. Это означает, что небольшие ошибки во входных данных приводят к огромным погрешностям в решении, что делает невозможной физическую интерпретацию поученного решения. Так в [5] показано, что для решения вида (4) 5%-ый шум во входном спектре
может быть очень мала. Это означает, что небольшие ошибки во входных данных приводят к огромным погрешностям в решении, что делает невозможной физическую интерпретацию поученного решения. Так в [5] показано, что для решения вида (4) 5%-ый шум во входном спектре ![]() может привести для ряда веществ к 100 % ошибке, а 10%-ый шум (например, для смеси веществ этилен, аммиак, метанол, этанол) уже к ошибкам порядка 1000%. Исходя из выше сказанного, обратная задача (3) относится к классу некорректно поставленных задач [1], для решения которой необходимо применение специальных методов решения, о которых будет рассказано в следующем разделе. Нужно отметить, что вслучае критически низкой обусловленности матрицы системы
может привести для ряда веществ к 100 % ошибке, а 10%-ый шум (например, для смеси веществ этилен, аммиак, метанол, этанол) уже к ошибкам порядка 1000%. Исходя из выше сказанного, обратная задача (3) относится к классу некорректно поставленных задач [1], для решения которой необходимо применение специальных методов решения, о которых будет рассказано в следующем разделе. Нужно отметить, что вслучае критически низкой обусловленности матрицы системы ![]() задачу следует сводить к идентификации не отдельных веществ, а классов веществ, для которых обусловленность системы будет гораздо выше. В этом случае можно говорить об идентификации в данном эксперименте какого-то вещества из данного класса и определения количественного вклада данного класса веществ.
задачу следует сводить к идентификации не отдельных веществ, а классов веществ, для которых обусловленность системы будет гораздо выше. В этом случае можно говорить об идентификации в данном эксперименте какого-то вещества из данного класса и определения количественного вклада данного класса веществ.
Процедуры численного решения обратной задачи
В настоящей работе предложены численные процедуры, позволяющие решать систему вида (3) за строго ограниченное время, что позволяет использовать их при построении систем дистанционного газоанализа, работающих в режиме реального времени.
Правая часть системы (3) содержит сигнатуры как целевых веществ, так и атмосферных составляющих. На предварительном этапе обработки экспериментального спектра ![]() проводится математическое моделирование спектра атмосферных составляющих, при этом не восстанавливаются точные значения концентраций атмосферных поглотителей. Полученный в результате математического моделирования спектр служит для выделения нормированного спектра целевых веществ, концентрации которых необходимо восстановить, при этом значительно сокращается размерность исходной линейной задачи, а, значит, и время необходимое на ее решение, что важно для систем, работающих в режиме реального времени.
проводится математическое моделирование спектра атмосферных составляющих, при этом не восстанавливаются точные значения концентраций атмосферных поглотителей. Полученный в результате математического моделирования спектр служит для выделения нормированного спектра целевых веществ, концентрации которых необходимо восстановить, при этом значительно сокращается размерность исходной линейной задачи, а, значит, и время необходимое на ее решение, что важно для систем, работающих в режиме реального времени.
Принимая во внимание аддитивность оптической плотности, можно записать разложение суммарного нормированного спектра на атмосферную составляющую и спектр целевых веществ:
|
|
где ![]() – смоделированный спектр атмосферной трассы,
– смоделированный спектр атмосферной трассы, ![]() – спектр целевых веществ. Ограничения на спектры запишутся в виде:
– спектр целевых веществ. Ограничения на спектры запишутся в виде:
| (5) |
Далее покажем, что моделирование атмосферного спектра можно проводить не только на основе спектров газовых составляющих, но и на основе спектров атмосферных трасс. Для этого рассмотрим Mатмосферных спектров ![]() , каждый из которых определяется вкладом поглотителей H2O, CO2, O3, NO2, N2O и некоторых других. Для смеси невзаимодействующих газов верно соотношение:
, каждый из которых определяется вкладом поглотителей H2O, CO2, O3, NO2, N2O и некоторых других. Для смеси невзаимодействующих газов верно соотношение:
|
|
где ![]() – j-й спектр (оптическая плотность) атмосферной трассы; i– номер атмосферного газа; j – номер экспериментального спектра атмосферы; N – число атмосферных газов;
– j-й спектр (оптическая плотность) атмосферной трассы; i– номер атмосферного газа; j – номер экспериментального спектра атмосферы; N – число атмосферных газов; ![]() – спектр i-го атмосферного газа;
– спектр i-го атмосферного газа; ![]() – относительная интегральная концентрация i-го составляющего атмосферы, соответствующая j-му атмосферному спектру
– относительная интегральная концентрация i-го составляющего атмосферы, соответствующая j-му атмосферному спектру ![]() , равная отношению текущей интегральной концентрации к концентрации, для которой получен референтный спектр. Для расчета атмосферного спектра используем линейную комбинацию спектров атмосферных трасс:
, равная отношению текущей интегральной концентрации к концентрации, для которой получен референтный спектр. Для расчета атмосферного спектра используем линейную комбинацию спектров атмосферных трасс:
| (6) |
где ![]() – спектр атмосферной трассы для текущего измерения,
– спектр атмосферной трассы для текущего измерения, ![]() – коэффициенты пропорциональности. Покажем возможность получения суммы следующего вида:
– коэффициенты пропорциональности. Покажем возможность получения суммы следующего вида:
|
|
где ![]() – относительные интегральные концентрации атмосферных составляющих, соответствующие экспериментальному спектру суммарной оптической плотности
– относительные интегральные концентрации атмосферных составляющих, соответствующие экспериментальному спектру суммарной оптической плотности ![]() ,
,
|
|
Коэффициенты пропорциональности при оптических плотностях будут иметь вид:
| (7) |
Таким образом, без шумов в спектрах и при выполнении условий линейности атмосферного спектра относительно спектров поглотителей, для разрешения системы (7) относительно ![]() (т.е. для того, чтобы была теоретическая возможность смоделировать любой атмосферный спектр в рамках линейной модели) необходимо, чтобы число спектром атмосферных трасс было не меньше числа основных атмосферных поглотителей
(т.е. для того, чтобы была теоретическая возможность смоделировать любой атмосферный спектр в рамках линейной модели) необходимо, чтобы число спектром атмосферных трасс было не меньше числа основных атмосферных поглотителей ![]() , а также, чтобы эти спектры были линейно независимы
, а также, чтобы эти спектры были линейно независимы ![]() .
.
Для реализации предложенного алгоритма создана база данных нормированных спектров атмосферных трасс, зарегистрированных при различных углах возвышения и различных погодных условиях (влажность, время года), что позволило получить наиболее независимые спектры. Размер базы определялся числом основных поглотителей атмосферы, существенных для приземных трасс в окне прозрачности атмосферы 700-1500 см-1.
Согласно (6) и с учетом (5) рассчитывается атмосферный спектр 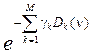 , невязка которого с экспериментальным спектром
, невязка которого с экспериментальным спектром ![]() минимальна. Для этого строится функционал вида:
минимальна. Для этого строится функционал вида:
|
(8)
|
где M– число спектров базы данных, используемых в оптимизации функционала; ![]() – коэффициенты пропорциональности;
– коэффициенты пропорциональности;![]() – весовая функция;
– весовая функция; 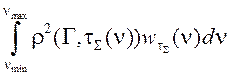 – квадрат невязки расчетного
– квадрат невязки расчетного 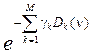 и экспериментального
и экспериментального ![]() спектров;
спектров; 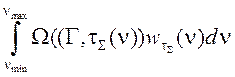 – штрафная функция, позволяющая проводить минимизацию на множестве, описываемом неравенством (5); α – параметр штрафной функции. Весовая функция нормирована на единицу и отражает спектральную ошибку:
– штрафная функция, позволяющая проводить минимизацию на множестве, описываемом неравенством (5); α – параметр штрафной функции. Весовая функция нормирована на единицу и отражает спектральную ошибку:
|
|
где ![]() – дисперсия спектральной ошибки, которая определяется как погрешность косвенных измерений:
– дисперсия спектральной ошибки, которая определяется как погрешность косвенных измерений:
|
|
Здесь ![]() – дисперсия спектральной ошибки в измеренном спектре
– дисперсия спектральной ошибки в измеренном спектре ![]() . Поскольку функционал (8) дифференцируем по Г, то для указанной оптимизации применяется метод градиентного спуска.
. Поскольку функционал (8) дифференцируем по Г, то для указанной оптимизации применяется метод градиентного спуска.
После моделирования спектра атмосферной трассы (точные значения концентраций атмосферных составляющих при этом не представляют интерес) вычисляют спектр целевых веществ:
| (9) |
В результате система (3) преобразуется к виду:
| (10) |
Спектр (9) может содержать сигнатуры одного или нескольких целевых веществ, причем неизвестно, каких именно. Решение СЛАУ (10) затрудняется некорректностью постановки задачи и слабой обусловленностью матрицы системы, о чем сказано в разделе постановка задачи. В настоящей работе предлагается следующий подход: вместо решения многомерной СЛАУ используется корреляционный анализ и определяется целевое вещество, спектр которого статистически наиболее близок к экспериментальному ![]() . Для этого предварительно создана база данных референтных спектров целевых веществ, где для известных концентраций
. Для этого предварительно создана база данных референтных спектров целевых веществ, где для известных концентраций ![]() хранятся референтные спектры
хранятся референтные спектры ![]() . При проведении корреляционного анализа для каждого вещества из базы данных и экспериментального спектра рассчитывается коэффициент корреляции:
. При проведении корреляционного анализа для каждого вещества из базы данных и экспериментального спектра рассчитывается коэффициент корреляции:
| (11) |
где 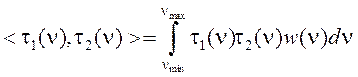 – скалярные произведения,
– скалярные произведения, 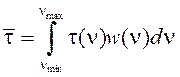 – средние значения,
– средние значения, ![]() – весовая функция. Вещество, для которого коэффициент корреляции оказался наибольшим и превысил заранее заданное пороговое значение, считается идентифицированным для задачи в постановке (10). Пороговые значения определяются эмпирически. Для восстановления концентраций минимизируется функционал вида:
– весовая функция. Вещество, для которого коэффициент корреляции оказался наибольшим и превысил заранее заданное пороговое значение, считается идентифицированным для задачи в постановке (10). Пороговые значения определяются эмпирически. Для восстановления концентраций минимизируется функционал вида:
| (12) |
где 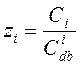 – относительные интегральные концентрации,
– относительные интегральные концентрации, ![]() – весовая функция, отражающая спектральную ошибку, а также учитывающая предварительные этапы обработки спектра. С учетом линейной зависимости спектральной ошибки σ и нормированного спектра τ, а также принимая во внимание (9), весовую функцию можно записать как
– весовая функция, отражающая спектральную ошибку, а также учитывающая предварительные этапы обработки спектра. С учетом линейной зависимости спектральной ошибки σ и нормированного спектра τ, а также принимая во внимание (9), весовую функцию можно записать как
|
|
|
|
Поскольку функционал (12) дифференцируем по Z, его оптимизация проводится методом градиентного спуска. После идентификации одного вещества и восстановления его концентрации из спектра (9) вычитается вклад этого вещества, и процедуры (11) и (12) повторяются заново. Таким образом, вместо решения многомерной СЛАУ предлагается решать одну или несколько одномерных задач, для которых выполнены условия корректности, и решения которой в обычных на практике условиях позволяют идентифицировать целевые вещества и их интегральные концентрации
Исследование влияния малых изменений входной информации на восстановленные концентрации
Покажем, что для разработанной методики решения обратной задачи шумы во входном спектре, сравнимые по значению с шумами в реальном эксперименте, приводят к ошибкам в решении не больше допустимых значений для данного класса аппаратуры и методики регистрации спектральных данных. В противном случае, если малые изменения во входной информации приводят к значительным изменениям решений задачи, невозможно говорить о физической интерпретации полученного решения. Среднеквадратическое значение шумовой составляющей в спектре ![]() , полученного на фурье-спектрорадиометре, постоянно во всем спектральном диапазоне. В этом случае можно говорить об аддитивной гауссовской модели шума в исходном спектре:
, полученного на фурье-спектрорадиометре, постоянно во всем спектральном диапазоне. В этом случае можно говорить об аддитивной гауссовской модели шума в исходном спектре:
| (13) |
где ![]() – спектр с учетом шумовой составляющей;
– спектр с учетом шумовой составляющей; ![]() – спектр без шума,
– спектр без шума, ![]() – аддитивный шум в спектре, с математическим ожиданием
– аддитивный шум в спектре, с математическим ожиданием ![]() и дисперсией
и дисперсией ![]() . Применяя зависимость (13), можно плавно изменять уровень входного шума sB в спектре
. Применяя зависимость (13), можно плавно изменять уровень входного шума sB в спектре ![]() и, зная точное значение концентрации целевого вещества в данном численном эксперименте, исследовать возможность идентификации целевого вещества, а также зависимость восстановленных интегральных концентраций от среднеквадратического значения шумовой составляющей спектра.
и, зная точное значение концентрации целевого вещества в данном численном эксперименте, исследовать возможность идентификации целевого вещества, а также зависимость восстановленных интегральных концентраций от среднеквадратического значения шумовой составляющей спектра.
В ходе вычислительных экспериментов проводилось математическое моделирование спектров атмосферной трассы при наличии целевого вещества (аммиака, как типичного вещества с узкополосным спектром, и изопропанола, как типичного вещества с широкополосным спектром). Для обоих случаев варьировались следующие параметры: исходная концентрация целевого вещества, температурный контраст, уровень шума в спектре трассы. Для заданных исходных концентраций целевого вещества и температурного контраста исследовалась зависимость относительной ошибки восстановления целевого вещества от уровня шума в спектре. Относительная ошибка восстановления концентрации веществ в конкретном эксперименте является случайной величиной, зависящей от реализации шума, как случайного процесса. На рис. 2 показана зависимость относительной ошибки восстановления концентрации аммиака от среднеквадратического значения входного шума, рабочее значение шума в исходном спектре ![]() составляет порядка
составляет порядка 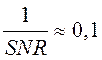 (SNR – отношение сигнал/шум), температурный контраст
(SNR – отношение сигнал/шум), температурный контраст ![]() 5º. Для каждого значения среднеквадратического шума рассчитано десять реализаций шумовой составляющей, и для каждой реализации получено значение ошибки восстановления. На рис. 2
5º. Для каждого значения среднеквадратического шума рассчитано десять реализаций шумовой составляющей, и для каждой реализации получено значение ошибки восстановления. На рис. 2 ![]() – относительная ошибка восстановленной концентрации. На рис. 3
– относительная ошибка восстановленной концентрации. На рис. 3 ![]() – среднеквадратическое значение относительной ошибки восстановленной концентрации.
– среднеквадратическое значение относительной ошибки восстановленной концентрации.
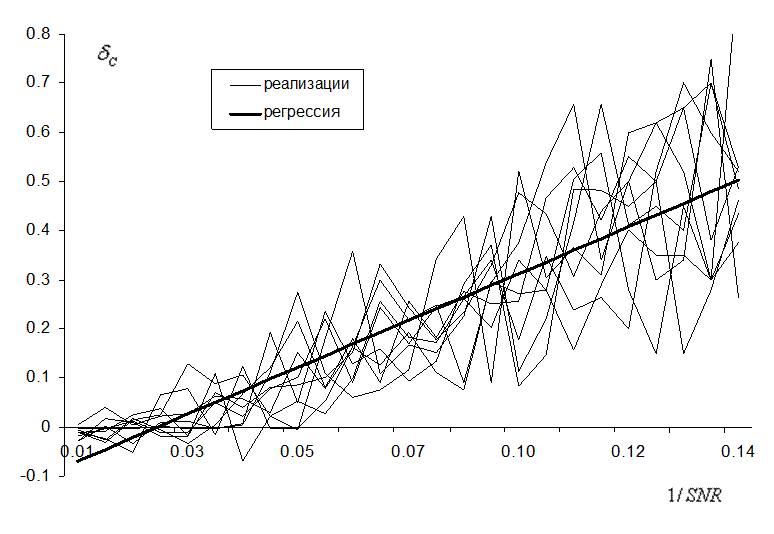
Рис. 2. Зависимость относительной ошибки восстановления концентрации аммиака от среднеквадратического значения входного шума на рабочем диапазоне шума. Жирной линией показана линейная регрессия.
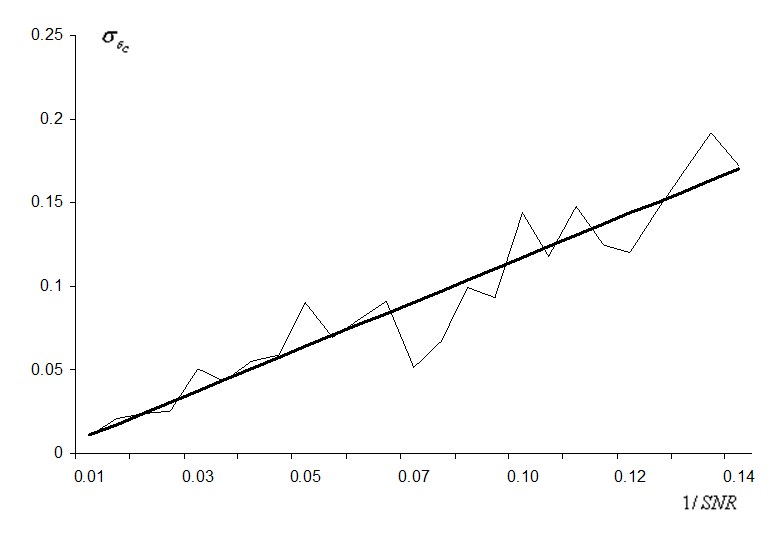
Рис. 3. Зависимость среднеквадратического значения относительной ошибки восстановления концентрации аммиака от среднеквадратического значения шума в спектре ![]() . Жирной линией показана линейная регрессия.
. Жирной линией показана линейная регрессия.
Из рис. 2 видно, что относительная ошибка имеет систематическую составляющую. Это объясняется тем, что для решения исходной задачи проводится математическое моделирование атмосферного спектра и, в итоге, вместо исходной СЛАУ решается одномерная система. В результате, появляется систематическая ошибка в решении, которой для больших значений шумов является определяющей в ошибке решения задачи. Применяя подобные численных эксперименты, можно выяснить при каких пороговых значения входных помех ошибка не превышает установленное допустимое значение и тем самым определить пределы применимости предлагаемой методики для разного типа веществ.
Далее проанализируем случайную составляющую относительной ошибки. Для восстановления концентрации идентифицированного вещества решается одномерная линейная задача:
| (14) |
Запишем оптическую плотность экспериментального спектра целевых веществ, выделив аддитивную шумовую составляющую:
|
|
где ![]() – зарегистрированное значение,
– зарегистрированное значение, ![]() – точное значение,
– точное значение, ![]() – шумы в экспериментальном спектре. Т.к. шумы на разных частотах входного спектра, вообще говоря, независимые случайные величины, то
– шумы в экспериментальном спектре. Т.к. шумы на разных частотах входного спектра, вообще говоря, независимые случайные величины, то
|
|
где ![]() – дисперсия шума на частоте νk,
– дисперсия шума на частоте νk, ![]() – символ Кронекера. Не нарушая общности, нормируем исходное уравнение на
– символ Кронекера. Не нарушая общности, нормируем исходное уравнение на ![]() :
:
|
|
Для нормированного уравнения верно равенство ![]() и
и ![]() , т.е. шум равномерный. Решение уравнения (14) будем искать в виде:
, т.е. шум равномерный. Решение уравнения (14) будем искать в виде:
| (15) |
где D – нормированная матрица уравнения. Решение ![]() уравнения (15) запишется в виде:
уравнения (15) запишется в виде:
| (16) |
Поскольку ![]() содержит шумы, то решение
содержит шумы, то решение ![]() является приближенным и запишется в виде
является приближенным и запишется в виде ![]() . Тогда решение вида (16) можно переписать отдельно для точного значения входной информации и для шумов:
. Тогда решение вида (16) можно переписать отдельно для точного значения входной информации и для шумов:
|
|
|
|
а поскольку Datm(ν) – величина расчетная, то очевидно что ![]() . Принимая во внимание (1) и экспоненциальную зависимость оптической плотности от нормированного коэффициента пропускания
. Принимая во внимание (1) и экспоненциальную зависимость оптической плотности от нормированного коэффициента пропускания ![]() , очевидно, что среднеквадратичное отклонение восстановленной концентрации
, очевидно, что среднеквадратичное отклонение восстановленной концентрации ![]() линейно зависит от среднеквадратичного значения шума во входном спектре
линейно зависит от среднеквадратичного значения шума во входном спектре ![]() , что видно на рис. 3. Далее можно показать количественную связь среднеквадратического отклонения восстановленной концентрации и среднеквадратического значения шума в исходном спектре
, что видно на рис. 3. Далее можно показать количественную связь среднеквадратического отклонения восстановленной концентрации и среднеквадратического значения шума в исходном спектре ![]() :
:
| (17) |
где ![]() – оптическая плотность для искомого вещества, соответствующая референтному спектру;
– оптическая плотность для искомого вещества, соответствующая референтному спектру; ![]() ;
; ![]() . В серии численных экспериментов показано, что количественные значения, описываемые зависимостью (17), и получаемые экспериментально являются величинами одного порядка. Расхождение в значениях коэффициентов пропорциональности можно объяснить тем, что для каждого нового численного эксперимента заново моделируется атмосферный спектр (7), что искажает спектр (9).
. В серии численных экспериментов показано, что количественные значения, описываемые зависимостью (17), и получаемые экспериментально являются величинами одного порядка. Расхождение в значениях коэффициентов пропорциональности можно объяснить тем, что для каждого нового численного эксперимента заново моделируется атмосферный спектр (7), что искажает спектр (9).
Заключение
Продемонстрированы численные процедуры решения обратной задачи спектроскопии, позволяющие на основе анализа единичного спектра собственного теплового изучения веществ в открытой атмосфере проводить их идентификацию и восстанавливать значения интегральных концентрации. Данная методика основывается на промежуточном моделировании атмосферного спектра; идентификации одного или нескольких целевых веществ корреляционными методами; решении вместо исходной многомерной СЛАУ одной или нескольких одномерных задач, для которых выполнены условия корректности, и решения которых в обычных на практике условиях позволяют восстанавливать интегральные концентрации целевых веществ.
Показано, что ошибка решения обратной задачи линейно возрастает с увеличением среднеквадратичного значения шума во входном спектре. В серии вычислительных экспериментов продемонстрировано, что значения относительной ошибки восстановления концентрации для рабочего уровня не превышают 30%, что является допустимым рабочим значением для беспробоотборных газоаналитических систем и методик. Методика реализована в программном комплексе и апробирована в серии как вычислительных, так и натурных испытаний и может быть использована для проведения дистанционного беспробоотборного газоанализа по единичному спектру.
Литература
[1] Тихонов А.Н., Арсенин В.Я. Методы решения некорректно поставленных задач. М: Наука, 1979. 285 с.
[2] Морозов А.Н., Светличный С.И. Основы фурье-спектрорадиометрии. М.: Наука, 2006. 275 с.
[3] Дворук С.К., Корниенко В.Н., Кочиков И.В. и др. Мониторинг загрязняющих веществ в атмосфере с помощью Фурье-спектрорадиометра // Опт. журн. 2004. Т. 71, № 5. С. 7-13.
[4] Кочиков И.В., Морозов А.Н., Светличный С.И., Фуфурин И.Л. Распознавание веществ в открытой атмосфере по единичной интерферограмме фурье-спектрорадиометра // Опт. и спектр. 2009. Т. 106, №5. С. 743-749.
[5] Козинцев В.И., Белов М.Л., Городичев В.А., Федотов Ю.В. Лазерный акусто-оптический анализ многокомпонентных газовых смесей. М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. 352 с.
Публикации с ключевыми словами: обратная задача, Фурье-спектрорадиометрия, молекулярная спектроскопия, идентификация веществ
Публикации со словами: обратная задача, Фурье-спектрорадиометрия, молекулярная спектроскопия, идентификация веществ
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||
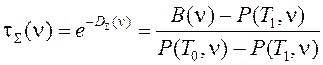 ,
, ,
,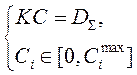 ,
,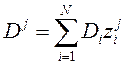 ,
,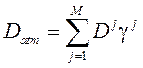 ,
,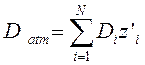 ,
,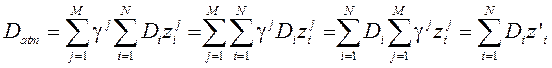 .
.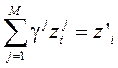
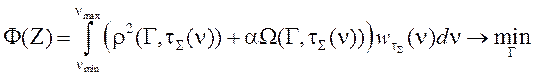 ,
,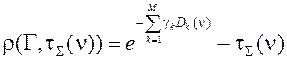 ,
,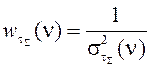 ,
,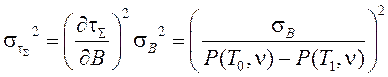 .
.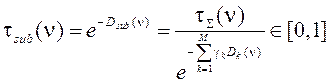 .
.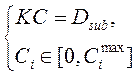 ,
,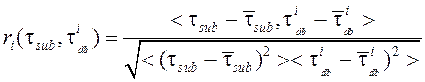 ,
,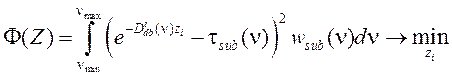 ,
,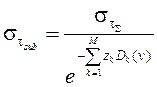 ,
,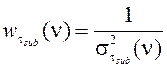 .
.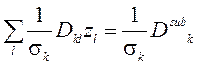 .
.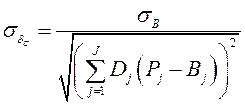 ,
,


