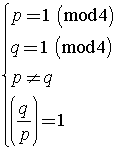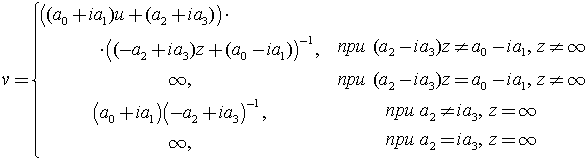научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2011
УДК 519.713.1; 519.177; 004.056.55
МГТУ им. Н.Э. Баумана
1. Введение
В задачах вычислительной математики, криптографии, математического моделирования часто применяются псевдослучайные последовательности. Причем такие последовательности должны быть неотличимы от истинно случайных последовательностей по своим статистическим свойствам. Для выработки таких последовательностей используют специальные алгоритмы – генераторы псевдослучайных последовательностей (ГПСП). В работах [3, 4] предлагается использовать клеточные автоматы в качестве элементов таких генераторов. Этот подход является многообещающим, так как ГПСП, основанные на клеточных автоматах, имеют очень высокую скорость работы, как при программной, так и при аппаратной реализации. Однако остается открытым вопрос о явном детерминируемом построении обобщенных клеточных автоматов для таких генераторов. Решению этого вопроса и посвящена настоящая статья.
2. Обобщенные клеточные автоматы
Классические клеточные автоматы впервые были предложены Дж. Фон Нейманом в работе [20]. Они активно исследовались (см. работы [15, 21-24]), в том числе и в контексте выработки псевдослучайных последовательностей. Недавно, в работах [3, 4], было предложено и исследовано обобщение клеточных автоматов – неоднородные клеточные автоматы. Такие автоматы мы будем называть обобщенными.
Назовем обобщенным клеточным автоматом пару ![]() , где
, где ![]() – ориентированный регулярный мультиграф (V – множество вершин, а E – мультимножество ребер) размера n, с каждой вершиной которого ассоциирована булева переменная, причем все вершины пронумерованы числами
– ориентированный регулярный мультиграф (V – множество вершин, а E – мультимножество ребер) размера n, с каждой вершиной которого ассоциирована булева переменная, причем все вершины пронумерованы числами ![]() . Переменную, ассоциированную с i-ой вершиной, будем обозначать
. Переменную, ассоциированную с i-ой вершиной, будем обозначать ![]() . Такие переменные мы будем называть ячейками. Для каждой вершины входящие в нее ребра пронумерованы числами
. Такие переменные мы будем называть ячейками. Для каждой вершины входящие в нее ребра пронумерованы числами ![]() .
.
Функция ![]() – локальная функция связи.
– локальная функция связи.
Обобщенный клеточный автомат работает следующим образом:
в начальный момент времени, каждая ячейка памяти ![]() ,
, ![]() имеет некоторое начальное значение
имеет некоторое начальное значение ![]() . Далее автомат работает по шагам. На шаге с номером tс помощью локальной функции связи вычисляются новые значения переменных:
. Далее автомат работает по шагам. На шаге с номером tс помощью локальной функции связи вычисляются новые значения переменных:
![]() ,
,
где ![]() – номер вершины, из которой исходит ребро, входящее в вершину i и имеющее номер j.
– номер вершины, из которой исходит ребро, входящее в вершину i и имеющее номер j.
Выходом обобщенного клеточного автомата на шаге с номером tявляются значения первых rячеек: ![]() . Соответственно, последовательность
. Соответственно, последовательность ![]() будем называть выходной последовательностью клеточного автомата.
будем называть выходной последовательностью клеточного автомата.
Поскольку клеточный автомат, очевидно, является конечным автоматом, выходная последовательность является периодической.
Рассмотрим частный случай обобщенных клеточных автоматов – неориентированный обобщенный клеточный автомат.
Назовем неориентированным обобщенным клеточным автоматом обобщённый клеточный автомат ![]() , где граф
, где граф ![]() такой, что для любого
такой, что для любого ![]() существует
существует ![]() .
.
Граф неориентированного обобщённого клеточного автомата можно рассматривать как неориентированный мультиграф, если каждую пару ребер вида ![]() и
и ![]() заменить на одно неориентированное ребро
заменить на одно неориентированное ребро ![]() . Такой автомат можно рассматривать как тройку
. Такой автомат можно рассматривать как тройку ![]() , где G – неориентированный мультиграф, f – локальная функция связи, а
, где G – неориентированный мультиграф, f – локальная функция связи, а ![]() – функция нумерации ребер, определенная выше.
– функция нумерации ребер, определенная выше.
Одними из важных криптографических характеристик клеточного автомата являются характеристики лавинного эффекта. Лавинный эффект представляет собой способность динамической системы существенно изменять выходную последовательность при небольших изменениях входных данных.
Рассмотрим два идентичных неориентированных обобщенных клеточных автомата ![]() и
и ![]() . Будем обозначать векторы их ячеек соответственно
. Будем обозначать векторы их ячеек соответственно ![]() и
и ![]() . Начальное заполнение отличается только в одной ячейке. Для определенности будем считать, что номер такой ячейки равен нулю (это не нарушает общности, поскольку перенумеровать переменные можно как угодно):
. Начальное заполнение отличается только в одной ячейке. Для определенности будем считать, что номер такой ячейки равен нулю (это не нарушает общности, поскольку перенумеровать переменные можно как угодно):
 .
.
Будем рассматривать две характеристики лавинного эффекта: интегральную и пространственную.
Интегральной характеристикой лавинного эффекта [3] назовем зависимость доли несовпадающих ячеек у двух конечных автоматов от номера такта:
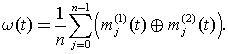
Пространственной характеристикой лавинного эффекта назовем зависимость отношения расстояния от вершины с номером 0 до самой дальней вершины, ячейка которой у двух автоматов не совпадает, к эксцентриситету вершины с номером 0:
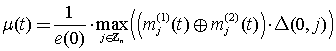 ,
,
где ![]() – длина минимального пути из вершины i в вершину j, а
– длина минимального пути из вершины i в вершину j, а ![]() – эксцентриситет вершины i.
– эксцентриситет вершины i.
Как показано в работе [4], для того, чтобы вероятности нулей и единиц в выходной последовательности обобщенного клеточного автомата совпадали, необходимо и достаточно, чтобы локальная функция связи являлась равновесной. Мы будем полагать ее таковой.
Мы будем рассматривать усредненные по достаточно большому количеству начальных заполнений интегральную и пространственную характеристику лавинного эффекта: ![]() и
и ![]() .
.
Начиная с некоторого ![]() , выполняется
, выполняется ![]() и
и ![]() при
при ![]() . Для обеспечений хороших статистических характеристик выходной последовательности необходимо, чтобы
. Для обеспечений хороших статистических характеристик выходной последовательности необходимо, чтобы ![]() , а
, а ![]() .
.
Для обеспечения хороших статистических свойств граф клеточного автомата должен быть таким, чтобы ![]() было как можно меньшим. Чтобы уменьшить эту величину следует использовать клеточный автомат, граф которого имеет возможно меньший диаметр.
было как можно меньшим. Чтобы уменьшить эту величину следует использовать клеточный автомат, граф которого имеет возможно меньший диаметр.
Диаметр Dрегулярного графа размера n степени kимеет следующую нижнюю оценку (граница Мура [8, 13]):
Учитывая тот очевидный факт, что ![]() , по-видимому, следует выбрать граф с диаметром, не слишком превосходящим границу Мура. Кроме того, для реализации лавинного эффекта граф должен быть таким, чтобы изменения одной ячейки клеточного автомата приводило к изменению все большего и большего числа ячеек с каждым шагом. Этим требованиям отвечают так называемые расширяющие графы (expandergraphs).
, по-видимому, следует выбрать граф с диаметром, не слишком превосходящим границу Мура. Кроме того, для реализации лавинного эффекта граф должен быть таким, чтобы изменения одной ячейки клеточного автомата приводило к изменению все большего и большего числа ячеек с каждым шагом. Этим требованиям отвечают так называемые расширяющие графы (expandergraphs).
3. Расширяющие графы
Теория расширяющих графов – сравнительно молодая область дискретной математики, нашедшая много приложений в математике и информатике. Этой теории посвящено большое количество литературы. Не задаваясь целью дать полный ее обзор, приведем здесь ссылки лишь на основные источники: [5, 7, 9, 10, 14, 17, 18]. Расширяющие графы применяются в ряде прикладных областей, в том числе, в задачах дерандомизации [18, 19] и для построения кодов, исправляющих ошибки [1]. Приведем здесь основные определения из этой теории.
Коэффициентом расширения неориентированного регулярного мультиграфа ![]() называется величина:
называется величина:
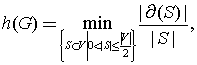
где ![]() – множество ребер, каждое из которых инцидентно ровно одной вершине из множества S.
– множество ребер, каждое из которых инцидентно ровно одной вершине из множества S.
Расширяющим графом (expandergraph) называется неориентированный регулярный мультиграф G, такой, что ![]() , где c – некоторая константа.
, где c – некоторая константа.
Коэффициент расширения графа связан с его спектральными свойствами. Так, рассмотрим отсортированный по убыванию спектр графа (то есть собственные числа его матрицы смежности):
![]() .
.
Как известно из спектральной теории графов [5], ![]() , где k– степень графа Gи справедливо следующее соотношение, называемое неравенством Чигера:
, где k– степень графа Gи справедливо следующее соотношение, называемое неравенством Чигера:
![]()
Для того, чтобы улучшить характеристики лавинного эффекта неориентированного клеточного автомата, основанного на расширяющем графе, следует, по-видимому, выбрать граф с возможно большим коэффициентом расширения графа. Учитывая то, что задача определения коэффициента расширения является вычислительно сложной, удовлетворимся выбором графа с величиной ![]() близкой к минимальной.
близкой к минимальной.
Согласно теореме Нили, нижняя граница для этой величины:
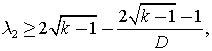
где D – диаметр графа.
К этой границе приближаются графы Рамануджана, то есть такие расширяющие графы, для которых справедливо неравенство
![]()
Для диаметра графов Рамануджана справедливо соотношение:
![]() .
.
Другими словами, диаметр графа Рамануджана всего в два раза больше границы Мура .
Учитывая близость графов Рамануджана к случайным графам по целому ряду свойств, можно ожидать, что для конечных автоматов, основанных на таких графах, ![]() будет близка к диаметру.
будет близка к диаметру.
Все это позволяет высказать гипотезу о том, что графы Рамануджана позволят обеспечить хорошие характеристики лавинного эффекта для основанных на них клеточных автоматах.
Одно из семейств графов Рамануджана – графы Любоцкого-Филипса-Сарнака (LPS-графы) [2, 11]. Одним из вариантов явных конструкций таких графов является конструкция, приведенная в книге [17]. Опишем ее здесь.
Выберем простые числа pи q, для которых выполняются условия:
Мы будем строить неориентированный мультиграф ![]() . Множеством вершин мультиграфа Vявляется проективная прямая над конечным полем
. Множеством вершин мультиграфа Vявляется проективная прямая над конечным полем ![]() , другими словами,
, другими словами, ![]() . Мультимножество ребер Eсостоит из всех пар
. Мультимножество ребер Eсостоит из всех пар ![]() , для которых выполняется:
, для которых выполняется:
для всех четверок ![]() , таких что:
, таких что:
· ![]() – нечетное положительное;
– нечетное положительное;
· ![]() – четные положительные;
– четные положительные;
· Выполняется условие:
В построенном таким образом графе могут быть кратные ребра (в том случае, когда выполняется и для ![]() и для
и для ![]() ) и петли. Степенью графа является количество решений уравнения , равное
) и петли. Степенью графа является количество решений уравнения , равное ![]() .
.
В книге [17] доказано, что этот граф является графом Рамануджана.
4. Применение графов Рамануджана в клеточных автоматах
Как было указано выше, для построения неориентированного обобщенного клеточного автомата достаточно задать его граф и локальную функцию связи, которая должна быть равновесной. Для обеспечения хороших криптографических свойств клеточного автомата, его локальная функция связи должна быть как можно более нелинейной. Способы построения равновесных булевых функций, нелинейность которых близка к максимальной, описаны, например, в книге [6].
Вычислительные эксперименты показали, что статистические свойства выходной последовательности лишь несущественно зависят от вида локальной функции связи, если она является равновесной и имеет близкую к максимальной нелинейность.
В качестве графа обобщенного клеточного автомата, мы будем использовать LPS-граф, конструкция которого приведена в предыдущем разделе. У полученного таким образом клеточного автомата имеется ![]() ячейка, а его граф имеет степень
ячейка, а его граф имеет степень ![]() . Числа pи qявляются простыми. На них накладываются приведенные в предыдущем разделе ограничения .
. Числа pи qявляются простыми. На них накладываются приведенные в предыдущем разделе ограничения .
Были проведены вычислительные эксперименты по определению характеристик лавинного эффекта построенных таким образом клеточных автоматов, при параметрах ![]() и
и ![]() , удовлетворяющих ограничениям . Во всех случаях, характеристики лавинного эффекта были близки к лучшим возможным теоретически: параметр
, удовлетворяющих ограничениям . Во всех случаях, характеристики лавинного эффекта были близки к лучшим возможным теоретически: параметр ![]() был близок к диаметру графа,
был близок к диаметру графа, ![]() и
и ![]() .
.
Были произведены исследования статистических свойств выходных последовательностей, при помощи тестов, рекомендованных NIST[16], по стандартной методике. При ![]() выходные последовательности автоматов проходили большинство тестов, в том числе такие важные тесты, как универсальный тест Маурера [12]. При
выходные последовательности автоматов проходили большинство тестов, в том числе такие важные тесты, как универсальный тест Маурера [12]. При ![]() последовательности проходили все тесты.
последовательности проходили все тесты.
В качестве примера рассмотрим LPS-граф размера 270 и степени 6 (![]() ,
, ![]() ), вид которого показан на Рис. 1, а характеристики лавинного эффекта соответствующего обобщенного клеточного автомата приведены на Рис. 2 и Рис. 3. У этого графа параметр
), вид которого показан на Рис. 1, а характеристики лавинного эффекта соответствующего обобщенного клеточного автомата приведены на Рис. 2 и Рис. 3. У этого графа параметр ![]() , а диаметр равен 5. Этот диаметр близок к минимально возможному для регулярных графов такой степени и такого размера диаметру, равному, согласно границе Мура , четырем. Из графиков видно, что
, а диаметр равен 5. Этот диаметр близок к минимально возможному для регулярных графов такой степени и такого размера диаметру, равному, согласно границе Мура , четырем. Из графиков видно, что ![]() , что близко к диаметру графа.
, что близко к диаметру графа.

Рис. 1. LPS-граф размера 270, степени 6.

Рис. 2. Усредненная пространственная характеристика лавинного эффекта.

Рис. 3. Усредненная интегральная характеристика лавинного эффекта.
Использование одного автомата не обеспечивает непредсказуемости. Поэтому, мы, основываясь на схеме, предложенной в работе [4], будем использовать два обобщенных клеточных автомата ![]() и
и ![]() разного размера с различными локальными функциями связи:
разного размера с различными локальными функциями связи: ![]() и
и ![]() . Выходные последовательности этих автоматов поразрядно складываются по модулю два (выбор именно сложения по модулю два связан с тем, что эта функция является корреляционно-иммунной). Функции
. Выходные последовательности этих автоматов поразрядно складываются по модулю два (выбор именно сложения по модулю два связан с тем, что эта функция является корреляционно-иммунной). Функции ![]() и
и ![]() , судя по результатам экспериментов, могут быть почти любыми равновесными, с нелинейностью, близкой к максимальной. Единственное условие, которое на них следует, по-видимому, наложить, это
, судя по результатам экспериментов, могут быть почти любыми равновесными, с нелинейностью, близкой к максимальной. Единственное условие, которое на них следует, по-видимому, наложить, это ![]() . Такая схема также существенно улучшает статистические свойства последовательности.
. Такая схема также существенно улучшает статистические свойства последовательности.
В качестве примера удачного сочетания параметров, для длины выхода ![]() , можно использовать размеры клеточных автоматов 270 и 282, как наиболее близкие к r. Для повышения эффективности реализации, степень графов должна быть наименьшей возможной, то есть равной 6.
, можно использовать размеры клеточных автоматов 270 и 282, как наиболее близкие к r. Для повышения эффективности реализации, степень графов должна быть наименьшей возможной, то есть равной 6.
Построенный таким образом ГПСП, при ![]() генерирует случайные последовательности, которые успешно проходят все статистические тесты, рекомендованные NIST.
генерирует случайные последовательности, которые успешно проходят все статистические тесты, рекомендованные NIST.
5. Заключение
Предложен способ детерминированного построения обобщенных клеточных автоматов, имеющих близкие к оптимальным характеристики лавинного эффекта. Генераторы псевдослучайных последовательностей, основанные на таких клеточных автоматах, вырабатывают последовательности, имеющие статистические свойства криптографического качества, что подтверждается успешным прохождением тестов, рекомендованных NIST. Такие генераторы могут найти применения как в криптографии и стеганографии, так и в различных областях математического моделирования.
Литература
1. Жуков Д.А. Асимптотически хорошие коды с линейной сложностью кодирования и декодирования // Дискретная математика и её приложения. – 2009. – №5. – С. 23-25.
2. Маргулис Г.А. Явные теоретико-групповые конструкции комбинаторных схем и их применения в построении расширителей и концентраторов // Пробл. передачи информ. – 1988. – Vol. 24, №1. – С. 51-60.
3. Сухинин Б.М. Исследование характеристик лавинного эффекта в двоичных клеточных автоматах с равновесными функциями переходов // Наука и образование: электронное научно-техническое издание. – 2010. – №8. – http://technomag.edu.ru/doc/159565.html.
4. Сухинин Б.М. Разработка генераторов псевдослучайных двоичных последовательностей на основе клеточных автоматов // Наука и образование: электронное научно-техническое издание. – 2010. – №9. – http://technomag.edu.ru/doc/159714.html.
5. Chung F.R.K. Regional conference series in mathematics,. Spectral graph theory. – Providence, R.I.: Published for the Conference Board of the mathematical sciences by the American Mathematical Society, 1997. – 207 p.
6. Cusick T.W., Stanica P. Cryptographic Boolean functions and applications. Academic Press, 2009.
7. Davidoff G.P., Sarnak P., Valette A. London Mathematical Society student texts. Elementary number theory, group theory, and Ramanujan graphs. – New York: Cambridge University Press, 2003. – 144 p.
8. Hoffman A., Singleton R. On Moore graphs with diameter 2 and 3, IBM Res // Develop. – 1960. – Vol. 4, P. 497–504.
9. Hoory S., Linial N., Wigderson A. Expander graphs and their applications // Bulletin-American Mathematical Society. – 2006. – Vol. 43, №4. – 439 p.
10. Krebs M., Shaheen A. Expander families and Cayley graphs. – Oxford ; New York: Oxford University Press, 2011.
11. Lubotzky A., Phillips R., Sarnak P. Ramanujan graphs // Combinatorica. – 1988. – Vol. 8, №3. – P. 261-277.
12. Maurer U.M. A universal statistical test for random bit generators // Journal of cryptology. – 1992. – Vol. 5, №2. – P. 89-105.
13. Miller M., Širán J. Moore graphs and beyond: A survey of the degree/diameter problem // Electronic Journal of Combinatorics. – 2005. – Vol. 61, P. 1-63
14. Morgenstern M. Existence and explicit constructions of q+ 1 regular Ramanujan graphs for every prime power q // Journal of Combinatorial Theory, Series B. – 1994. – Vol. 62, №1. – P.44-62.
15. Packard N.H., Wolfram S. Two-dimensional cellular automata // Journal of Statistical Physics. – 1985. – Vol. 38, №5. – P.901-946.
16. Rukhin A., идр. A statistical test suite for random and pseudorandom number generators for cryptographic applications (SP 800-22). NIST, 2010.
17. Sarnak P. Cambridge tracts in mathematics. Some applications of modular forms. – Cambridge ; New York: Cambridge University Press, 1990. – 111 p.
18. Vadhan S. The unified theory of pseudorandomness // ACM SIGACT News. – 2007. – Vol. 38, №3. – P. 39-54.
19. Vadhan S.P. Pseudorandomness // Foundations and Trends in Theoretical Computer Science. – 2010. – 200 p.
20. Von Neumann J. The general and logical theory of automata // Cerebral mechanisms in behavior. – 1951. – P. 1–41.
21. Wolfram S. Cryptography with cellular automata //: Springer, 1986. - P. 429-432.
22. Wolfram S. Statistical mechanics of cellular automata // Reviews of Modern Physics. – 1983. – Vol. 55, №3. – 601 p.
23. Wolfram S. Theory and applications of cellular automata // Advanced Series on Complex Systems, Singapore: World Scientific Publication, 1986. – 1986. – Vol. 1.
24. Wolfram S. Universality and complexity in cellular automata // Physica D: Nonlinear Phenomena. – 1984. – Vol. 10, №1-2. – P. 1-35.
Публикации с ключевыми словами: криптография, клеточный автомат, расширяющий граф, псевдослучайная последовательность
Публикации со словами: криптография, клеточный автомат, расширяющий граф, псевдослучайная последовательность
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||