научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#2 Февраль 2005
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ НА ОСНОВЕ ФРАКТАЛЬНЫХ ФУНКЦИЙ
![]()
УДК 517.9
Кравченко Олег Викторович
средняя школа № 166, 10 класс
Научный руководитель:
Масюк Владимир Михайлович,
Институт радиотехники и электроники РАН
Введение
В последние годы прошлого столетия усилия многих ученых были направлены на исследования в области фрактальной геометрии и ее применению в различных областях физики, радиофизики, антенной техники.
Результаты этих исследований были основаны на фрактальной геометрии [1–4]. Например, введение фракталов при решении задач антенной техники [5–8] обеспечило следующие пути их исследования:
а) изучение самих фрактальных элементов антенны,
б) использование фракталов в разработке антенных решеток.
Термин «фрактал» (от лат. frangere – «ломать» и fractus – «дробный») был введен в 1975 г. Бенуа Б. Мандельбротом и основан на теории фрактальной (дробной) размерности Хаусдорфа [1], предложенной в 1919 году. Мандельброту удалось найти практическое применение множеству Кантора, функциям Вейерштрасса, которые считались неперспективными из-за того, что они не определяются в терминах евклидовой геометрии. В свое время эти функции рассматривались лишь как бесполезные математические курьезы.
Фракталы можно подразделить на детерминированные (созданные с помощью детерминированных правил), случайные (созданные с помощью комбинации порождающих правил, выбранных наугад в разных масштабах) [2], а также полученные методами детерминированного хаоса. Во фрактальной статистике говорят о фрактальных распределениях (Парето, Леви и т.д.)
Таким образом, идеи Мандельброта послужили также началом систематического изучения фракталов в различных прикладных задачах. Сегодня известны применения фракталов в теории электромагнитного поля, обнаружении малоконтрастных (скрытых) целей в радиолокации и теории антенн. Фрактальные модели обычно строятся на основе различных математических алгоритмов с использованием современной компьютерной графики [1, 2].
Рассмотрена проблема построения различных классических фрактальных функций, обладающих следующими основными свойствами: самоподобием, масштабированием, дробной размерностью.
Целью данной работы является краткий обзор последних научных достижений в области использования фрактальной геометрии при проектировании элементов и устройств антенн, а также уделено большое внимание получению вычислительных алгоритмов.
Алгоритмы построения фрактальных функций
Классические фрактальные функции
Рассмотрим наиболее известные классические фрактальные функции (рис. 1). Приведем формальные определения для таких топологических понятий, как, например, линия:
1. Пусть в р-мерном пространстве ![]() с координатами
с координатами ![]() имеется р
непрерывных функций
имеется р
непрерывных функций ![]() или
или ![]() , заданных на отрезке [
, заданных на отрезке [![]() ]. Тогда уравнения
]. Тогда уравнения ![]() определяют в
параметрическом виде непрерывную кривую в
определяют в
параметрическом виде непрерывную кривую в ![]() , соединяющую точки
, соединяющую точки ![]() и
и ![]() . Определенная
таким образом линия представляет собой упорядоченное множество точек, порядок
обхода которых задается прямым перебором порядкам точек отрезка [
. Определенная
таким образом линия представляет собой упорядоченное множество точек, порядок
обхода которых задается прямым перебором порядкам точек отрезка [![]() ]. Эта кривая может
иметь точки самопересечения, т. е. такие точки
]. Эта кривая может
иметь точки самопересечения, т. е. такие точки ![]() и
и ![]() , которые имеют одинаковые
координаты
, которые имеют одинаковые
координаты ![]() .
Здесь точки
.
Здесь точки ![]() считаются
различными.
считаются
различными.
2. Определение Кантора. Канторовской кривой на плоскости называется континуум, в окрестности каждой точки которого имеются точки плоскости, не принадлежащие континууму.
Это определение линии на плоскости было дано Кантором в 1870 г. и является обобщением предыдущего. Под это определение подпадает такой класс линий, как ковер Серпинского, который может быть получен как непрерывный образ отрезка.
3. Определение Урысона. Линия –
одномерный континуум (связанное компактное метрическое пространство С, каждая
точка которого обладает сколь угодно малой окрестностью с границей размерности
нуль), т.е. для ![]() пространство
С может быть представлено в виде суммы конечного числа множеств диаметра
меньшего
пространство
С может быть представлено в виде суммы конечного числа множеств диаметра
меньшего![]() ,
при этом никакие три из этих множеств не имеют общей точки. На сегодняшний день
определение линии Урысона является наиболее общим. Этому определению
удовлетворяют привычные кривые, канторовы множества, а также универсальная
кривая Менгена и др.
,
при этом никакие три из этих множеств не имеют общей точки. На сегодняшний день
определение линии Урысона является наиболее общим. Этому определению
удовлетворяют привычные кривые, канторовы множества, а также универсальная
кривая Менгена и др.

Функция Больцано
В 1830 г. Больцано в работе «Учение о функции» [6] строит пример непрерывной нигде недифференцируемой функции. Приведем построение двух вариантов классической недифференцируемой функции Больцано, отличающихся вычислительными алгоритмами.
Алгоритм 1.
1. Обозначим функцию Больцано через ![]() . Определим
вспомогательную функцию
. Определим
вспомогательную функцию ![]() и изложим на примере
последовательность построения
и изложим на примере
последовательность построения ![]() . Для этого отрезок АВ делим четыре
равные части и заменяем его ломаной ABCDE. Ее точки имеют координаты
. Для этого отрезок АВ делим четыре
равные части и заменяем его ломаной ABCDE. Ее точки имеют координаты ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Поместим точку
(p,q) в начало координат (рис. 2, а). Назовем такую
операцию B-операцией. Пусть графиком функции
. Поместим точку
(p,q) в начало координат (рис. 2, а). Назовем такую
операцию B-операцией. Пусть графиком функции ![]() является отрезок
является отрезок ![]() и
и ![]() . Применив к этим
точкам B‑операцию, получаем точки
. Применив к этим
точкам B‑операцию, получаем точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Это определяет функцию
. Это определяет функцию ![]() и её график
и её график ![]() . На рис. 2, a
изображены графики функций
. На рис. 2, a
изображены графики функций ![]() .
.
2. Применяя B‑операцию
к каждой паре точек ![]() ;
; ![]() ; …, получим следующие точки:
; …, получим следующие точки: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,… Определим
функцию
,… Определим
функцию ![]() ,
полагая, что ее графиком является ломаная
,
полагая, что ее графиком является ломаная ![]() . На рис. 2, б изображены графики
функций
. На рис. 2, б изображены графики
функций ![]() ,
а на рис. 2, в - поведение функций
,
а на рис. 2, в - поведение функций ![]() .
.
 3. Повторив эту операцию n раз, придём к
функции
3. Повторив эту операцию n раз, придём к
функции ![]() .
Вершины графика
.
Вершины графика ![]() имеют
абсциссы
имеют
абсциссы ![]() ,
т.е.
,
т.е. ![]() +1
точек. Колебание функции
+1
точек. Колебание функции ![]() в каждом из промежутков
в каждом из промежутков
![]() (1)
(1)
будет
![]() . (2)
. (2)
Если ![]() (
(![]() ), то
), то ![]() и точка
и точка ![]() совпадает с точкой
совпадает с точкой ![]() . Согласно
построения функции, однозначно определим функцию Больцано
. Согласно
построения функции, однозначно определим функцию Больцано ![]() при значениях
при значениях ![]() (
(![]() ,
, ![]() ), полагая
), полагая ![]() .
.
Следовательно, график функции ![]() проходит через вершины всех
ломаных
проходит через вершины всех
ломаных ![]() .
Колебание
.
Колебание ![]() на
любом множестве точек
на
любом множестве точек ![]() , принадлежащем промежутку
, принадлежащем промежутку ![]() , будет меньше
, будет меньше ![]() , поэтому
, поэтому ![]() будет непрерывна
на множестве
будет непрерывна
на множестве ![]() .
При других значениях x функция
.
При других значениях x функция ![]() определяется предельным переходом
определяется предельным переходом ![]() . Таким образом,
функция Больцано определена на отрезке
. Таким образом,
функция Больцано определена на отрезке ![]() . Приведенный алгоритм прост в реализации,
но требует построения итеративного аглоритма с учетом всех вспомогательных
функций
. Приведенный алгоритм прост в реализации,
но требует построения итеративного аглоритма с учетом всех вспомогательных
функций ![]() .
.
Алгоритм 2.
Второй алгоритм основан на свойствах рядов (1), (2) . Для его реализации
требуется построить ряд, сумма которого является функцией Больцано. Для этого
зададим на отрезке АС ломаные линии ![]() . Функция
. Функция ![]() задана отрезком АВ,
задана отрезком АВ, ![]() – ломаной, звенья
которой являются боковыми сторонами треугольника с основанием АС и высотой
– ломаной, звенья
которой являются боковыми сторонами треугольника с основанием АС и высотой ![]() ,
, ![]() – ломаной,
образованной боковыми сторонами четырех треугольников с основаниями
– ломаной,
образованной боковыми сторонами четырех треугольников с основаниями ![]() и высотой
и высотой ![]() (см. рис. 3а).
Продолжая этот процесс, перейдем к функции
(см. рис. 3а).
Продолжая этот процесс, перейдем к функции ![]() . Этот ряд сходится равномерно, его
сумма с бесконечным верхним пределом дает функцию, непрерывную на
. Этот ряд сходится равномерно, его
сумма с бесконечным верхним пределом дает функцию, непрерывную на ![]() .Эта функция нигде
не имеет производной. При вычислениях и проектировании реальных дискретных
систем построение функции Больцано, как правило, ограничивается на шаге N
(исходя из требований к точности приближения), поэтому алгоритм построения
.Эта функция нигде
не имеет производной. При вычислениях и проектировании реальных дискретных
систем построение функции Больцано, как правило, ограничивается на шаге N
(исходя из требований к точности приближения), поэтому алгоритм построения ![]() можно упростить.
Для этого строим ряд вида
можно упростить.
Для этого строим ряд вида ![]() , где
, где ![]() – ломаные, образованные боковыми сторонами
треугольников с основанием
– ломаные, образованные боковыми сторонами
треугольников с основанием ![]() и высотой
и высотой ![]() , как показано на рис. 3б.
Функция
, как показано на рис. 3б.
Функция ![]() строится
по простому итеративному закону, ее значения на каждом из интервалов
строится
по простому итеративному закону, ее значения на каждом из интервалов ![]() (см.
рис. 3в)
(см.
рис. 3в)
![]() 1 –1 –1 –1 ;
1 –1 –1 –1 ;
![]() 1 –1 –1 –1 –1 1 1 1 –1 1 1 1 –1 1 1
1.
1 –1 –1 –1 –1 1 1 1 –1 1 1 1 –1 1 1
1.
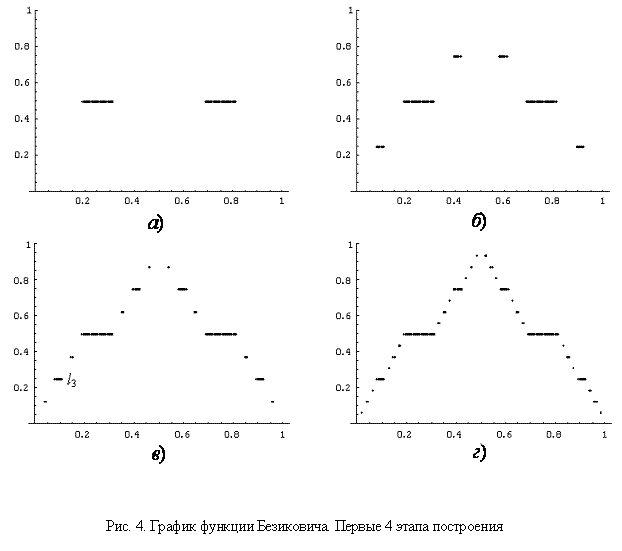
Функция Безиковича
Примером непрерывной функции, которая не имеет ни в
одной точке ни конечной, ни бесконечной односторонней производной является
функция Безиковича [6]. Для построения данной функции существует эффективный
итерационный процесс, состоящий из следующих этапов. На первом этапе строим
отрезок длиной 2а на прямой. Далее, так как функция симметрична относительно
точки а, будем проводить ее построение на интервале (0, а). Затем в центральной
части этого интервала строим отрезок длиной l1=a/4. Интервал (0, а) делится отрезком l1 на две равные части, а в центре каждого из них
располагаются соответственно новые отрезки ![]() . Таким образом, получаем четыре
равных интервала, в середине которых размещаются отрезки длиной
. Таким образом, получаем четыре
равных интервала, в середине которых размещаются отрезки длиной ![]() и т.д. Общее
выражение для длины отрезка на i-й итерации
и т.д. Общее
выражение для длины отрезка на i-й итерации ![]() . В итоге на отрезке
. В итоге на отрезке ![]() построено
бесконечное множество отрезков
построено
бесконечное множество отрезков ![]() объединение которых L – всюду плотное
множество с суммарной длиной
объединение которых L – всюду плотное
множество с суммарной длиной ![]() . В итоге получаем функцию Безиковича,
график которой приведен для первых 4-х итераций на рис. 4. Непрерывная функция,
построенная таким образом, не имеет ни в одной точке, ни правой, ни левой
производной.
. В итоге получаем функцию Безиковича,
график которой приведен для первых 4-х итераций на рис. 4. Непрерывная функция,
построенная таким образом, не имеет ни в одной точке, ни правой, ни левой
производной.
Построение начинается с выбрасывания средней трети отрезка (рис.5), т.е. из исходного множества [–1, 1] удаляем открытый интервал [–1/3, 1/3]. На следующем и всех последующих шагах удаляем среднюю треть всех отрезков текущего уровня. По приведенной процедуре легко построить итерационную процедуру. Другими словами, части множества подобны целому множеству. Это свойство самоподобия называют также масштабной инвариантностью или скейлингом. Построение, аналогичное проведенному выше, можно проделать, осуществляя деление отрезка не на три, а на большее число частей п. Длина выброшенной части отрезка по-прежнему равна 1, а остающееся множество не содержит ни одного целого интервала. Свойство самоподобия сохраняется. Про все такие множества говорят, что они обладают канторовой структурой.
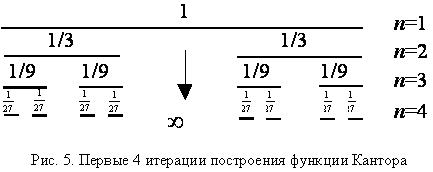
Функция Ван-дер-Вардена
Пусть ![]() ,
, ![]() – функция, равная расстоянию от точки
x до ближайшей целочисленной точки,
– функция, равная расстоянию от точки
x до ближайшей целочисленной точки,
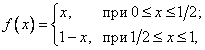
где
![]() .
Функция
.
Функция ![]() –
непрерывная на всей числовой оси, периодическая с периодом 1, линейная на
каждом отрезке
–
непрерывная на всей числовой оси, периодическая с периодом 1, линейная на
каждом отрезке ![]() ,
где s – целое число, а угловой коэффициент графика
,
где s – целое число, а угловой коэффициент графика ![]() на каждом отрезке
равен
на каждом отрезке
равен ![]() .
Пусть
.
Пусть ![]() ,
, ![]() . Функция
. Функция ![]() определяет
расстояние между точкой x и ближайшей к ней точке
определяет
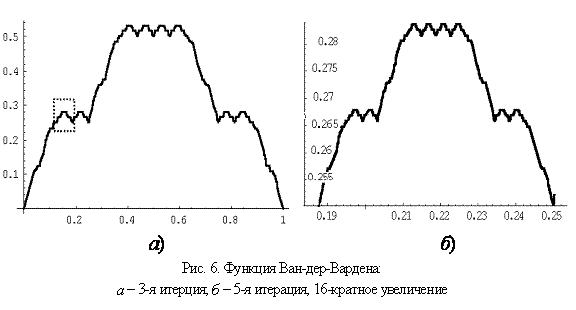
расстояние между точкой x и ближайшей к ней точке ![]() . График функции Ван-дер-Вардена
приведен на рис. 6. Разработанная итерационная формула расчета функции
Ван-дер-Вардена имеет вид
. График функции Ван-дер-Вардена
приведен на рис. 6. Разработанная итерационная формула расчета функции
Ван-дер-Вардена имеет вид
![]()
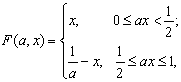 (3)
(3)
 Функции Серпинского
Функции Серпинского
Двумерным аналогом функции Кантора является ковер Серпинского [2]. Рассмотрим вначале этапы построения треугольного ковра Серпинского. Пусть Т – заданный правильный треугольник, А, В, С – его вершины: левая, верхняя и правая. Соединяя середины сторон треугольника Т, получим четыре новых правильных треугольника, три из которых – Т0, Т1, Т2, содержат вершины А, В, С, расположенные параллельно Т, и четвертый треугольник U находится в центре треугольника Т; исключаем внутреннюю область треугольника U.
Произведем над каждым треугольником Т0, Т1,
Т2 те же операции как и для треугольника Т: получим девять
треугольников, расположенных параллельно треугольнику Т. На n-ом шаге имеем ![]() ;
; ![]() – новые треугольники. На рис. 7 приведен
ковер Серпинского при
– новые треугольники. На рис. 7 приведен
ковер Серпинского при ![]() .
.
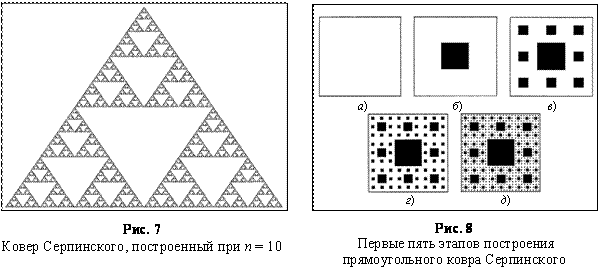
Также построим прямоугольный ковер Серпинского. Берем квадрат со стороной, равной единице. На первом шаге делим его на 9 равных квадратов (со стороной 1/3), и все внутренние точки центрального квадрата удаляем (на рис. 8 эта часть выделена черным цветом). На втором шаге также поступаем с оставшимися 8 квадратами, причем возникают уже 64 квадрата (со стороной 1/9). Далее процесс повторяем на всё более и более мелких масштабах. Нетрудно найти, что суммарная площадь выброшенных квадратов
![]() , (4)
, (4)
как это имело место и в случае канторова множества. Оставшееся множество точек называется ковром Серпинского. Как видно из приведенного построения, достаточно задать алгоритм одного шага преобразования, чтобы восстановить структуру фрактала на любых масштабах.
Отметим, что до сих пор рассматривалось построение фрактала с помощью какого-либо детерминированного алгоритма, однако может использоваться и вероятностный алгоритм. При этом свойство самоподобия у таких фракталов сохраняется «в среднем», т.е. после серии реализаций или серии масштабных преобразований.
Рассмотрим общий метод получения аналогичных
отображений. В отличие от рассмотренных ранее нелинейных точечных отображений
рассмотрим теперь системы линейных функций (отображений), задающих аффинные
преобразования плоскости. Каждое из преобразований ![]() системы можно записать в
виде
системы можно записать в
виде ![]() ,
,
![]() . (5)
. (5)
Здесь матрица А осуществляет масштабирование исходного
множества, а вектор b – сдвиг. Отображения должны быть сжимающими: ![]() .
.
Систему функций получим, рассматривая совместно набор
п отображений Т = {![]() }.
}.
Алгоритм действия отображения Т состоит в следующем. Зададим некоторое компактное начальное множество точек Е0 на плоскости. Первое применение Т к этому множеству (т.е. первая итерация) дает множество
![]() , (6)
, (6)
т. е.
каждое из отображений ![]() должно быть применено к исходному
множеству, а затем требуется объединить получившиеся множества. Следующие
итерации можно записать в следующем виде:
должно быть применено к исходному
множеству, а затем требуется объединить получившиеся множества. Следующие
итерации можно записать в следующем виде:
![]() . (7)
. (7)
Системой итерированных функций (СИФ) называется
совокупность отображений ![]() , описываемая (5)–(7) согласно
приведенной итерационной схеме
, описываемая (5)–(7) согласно
приведенной итерационной схеме
В качестве примера рассмотрим систему из отображений
для салфетки Серпинского (Е0 – треугольник с вершинами (0,0),
(1,0), (1/2, ![]() ),
),
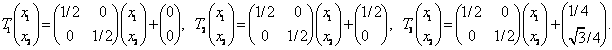 Каждое из этих отображений – сжимающее, со
степенью сжатия s = 1/4.
Каждое из этих отображений – сжимающее, со
степенью сжатия s = 1/4.
Применение фракталов в антенной технике
На основе идей и алгоритмов, рассмотренных ранее в первом разделе, был предложен новый метод методы использования фрактальных элементов в антенных решетках. Его применение позволяет повысить плотность размещения и снизить взаимосвязи между элементами. Кроме того, на основе фрактальной теории были изучены свойства и вид излучения таких антенн [5–8]. Использование фрактальной теории позволяет получить антенны, которые являются электрически длинными, но физически компактны и занимают малую площадь. Благодаря этому свойству можно добиться миниатюризации антенн.
От современных антенн требуется высокая точность и минимальные размеры. Для радиосвязи требуются системы, которые могут работать на максимальном количестве диапазонов частот. Бортовые антенные системы требуют от антенн максимально возможной миниатюризации. Для достижения этих целей были предложены различные методы применения фракталов в теории антенн. Покажем возможные области применения фракталов в антенной технике:
а) проволочные антенны, микрополосковые антенны – эти антенны имеют физическую фрактальную структуру;
б) антенны с фрактальной диаграммой направленности (ДН), решетки с фрактальным распределением тока – антенны построены на основе компьютерного моделирования фрактальных характеристик.
Приведем пример использования фрактальной структуры для простой кольцевой антенны [5].
Излечение решетки будет иметь вид:
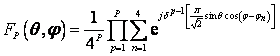 (8)
(8)
Р – общее количество циклов; N =4 –
количество элементов на одном кольце; ![]() –
фаза (сдвиг) элемента,
–
фаза (сдвиг) элемента, ![]() ;
; ![]() – масштабный фрактальный
коэффициент.
– масштабный фрактальный
коэффициент.

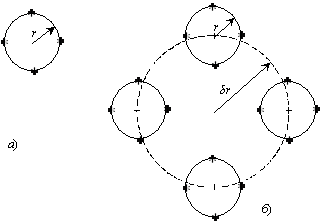
Рис. 9. Геометрия плоской фрактальной решетки
Так, меняя количество циклов Р и значение масштабного
коэффициента, можно получать антенны с различными видами излучения. На полученных графиках (рис. 10) отчетливо видна симметрия,
обусловленная фрактальной структурой решетки. Из этих графиков можно получить
еще одно важное характеристическое свойство антенны – насколько хорошо она
принимает и усиливает сигнал в основном направлении и насколько подавляет
ненужное излучение с других направлений. Эти характеристики задаются в виде
графиков “боковых лепестков” в логарифмическом масштабе в диапазоне углов ![]() или
или ![]() .
.
![]()
![]()
![]()
![]()
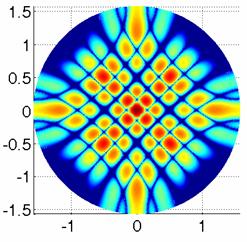
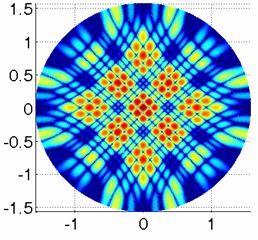
Рис. 10. Вид излучения антенной решетки
а) ![]() ; б)
; б) ![]() .
.
Из рис. 11 можно заключить, что полученная антенная решетка ослабляет паразитное излучение не менее чем на 6 дБ.
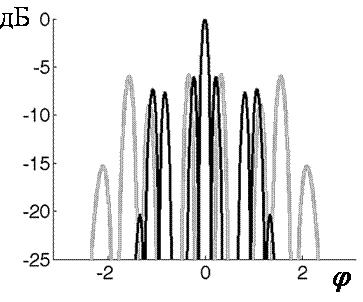
Рис. 11. График боковых лепестков
Введение более сложных фрактальных структур, например, треугольных кольцевых решеток с центральным элементом, позволяет значительно улучшить характеристики антенны.
![]()
![]()
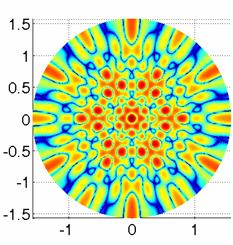
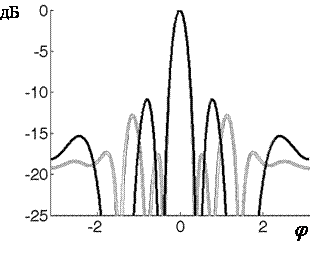
Рис. 12. График боковых лепестков для треугольной антенны
Здесь видно (рис. 12), что
такая антенная решетка ослабляет паразитное излучение на 11 дБ. Черным цветом
на рис. 11 и рис. 12 обозначен уровень боковых лепестков в направлении ![]() , серым - при
, серым - при ![]() .
.
Выводы и результаты
В результате работы были изучены различные виды фракталов, получены численные алгоритмы построения некоторых фракталов с использованием различных математических пакетов. Отдельно представлено программное обеспечение на Matlab, Mathematica 4.0 и Borland Pascal.
Анализ обширной литературы по этой проблеме позволил сделать следующие выводы:
1. Большое количество работ за последние годы как за рубежом, так и у нас в стране, говорит о перспективности данного направления использования фракталов.
2. Фракталы используются не только в математических исследованиях, но и находят широкое применение во многих областях науки и техники.
3. Использование фракталов позволяет получить быстрые вычислительные алгоритмы. Они основаны как на детерминированных правилах (итерационные или рекурсивные процедуры), так и на хаотических, с применением теории математической статистики.
4. Очень широко представлено применение фракталов в антенной технике. Так на примере было показано, что использование фрактальной организации позволяет строить антенны, имеющие меньшее число элементов и в ряде случаев лучшие характеристики по сравнению с традиционными, при этом обеспечивается простота их анализа.
Список литературы
1. Mandelbrot B.B. Fractals: form, chance and dimension. - San Francisko: Freeman, 1977.
2. Кроновер Р.М. Фракталы и хаос в динамических системах. Пер. с англ. – М.: Постмаркет, 2000.
3. Глейк Дж.Хаос. Создание новой науки. – Санкт-Петербург: Амфора, 2001.
4. Пайтген Х.О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. – М.: Мир, 1993.
5. Werner D.H. and Ganguly S. An Overview of the Fractal Antenna Engineering Research, IEEE Antennas and Propagation Magazine. – 2003. - vol. 45. - no. 1. - pp. 38–57.
6. Басараб М.А., Кравченко В.Ф., Масюк В.М. R-функции, атомарные функции и их применение – Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. – 2001. - № 8. - С. 5–40.
7. Кравченко В.Ф. Лекции по теории атомарных функций и некоторым их приложениям. – М: Радиотехника, 2003.
8. Кравченко В.Ф., Басараб М.А. Булева алгебра и методы аппроксимации в краевых задачах электродинамики. – М.: Физматлит, 2004.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||