научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2009
А.Э. Антух
МГТУ им. Н.Э. Баумана, 105005, Москва,
2-я Бауманская ул., д.5.
Введение
Оптимизация с использованием роя частиц (Particle Swarm Optimization, PSO) – это метод поиска, который базируется на понятии популяции и моделирует поведение птиц в стае и косяков рыб. Первоначальной целью использования концепции роя частиц была графическая имитация красивого и непредсказуемого движения птиц или рыб в стае с целью обнаружения базовых принципов, благодаря которым птицы летают (рыбы плавают) синхронно и умеют менять направление движения с перегруппировкой в оптимальные формации. С тех пор концепция развилась в простой и перспективный оптимизационный метод.
В PSO-методе агентами являются частицы в пространстве параметров задачи оптимизации. В каждый момент времени (на каждой итерации) частицы имеют в этом пространстве некоторое положение и вектор скорости. Для каждого положения частицы вычисляется соответствующее значение целевой функции, и на этой основе по определенным правилам частица меняет свое положение и скорость в пространстве поиска.
В основу метода PSO положена социально-психологическая поведенческая модель толпы. Существует несколько разновидностей метода. В каноническом методе роя частиц, предложенном в 1995 году в работе Kennedy, Eberhart [3], на каждой итерации при определении следующего положения частицы учитывается информация о наилучшей частице из числа «соседей» данной частицы, а также информация о данной частице на той итерации, когда этой частице соответствовало наилучшее значение целевой функции.
1. Описание метода
Будем рассматривать задачу глобальной безусловной минимизации целевой функции ![]() в
в ![]() -мерном арифметическом пространстве
-мерном арифметическом пространстве ![]() :
:
![]() . (1)
. (1)
Множество частиц обозначим ![]() , где
, где ![]() - количество частиц в рое (размер популяции). В момент времени
- количество частиц в рое (размер популяции). В момент времени ![]() координаты частицы
координаты частицы ![]() определяются вектором
определяются вектором ![]() , а ее скорость - вектором
, а ее скорость - вектором ![]() . Начальные координаты и скорости частицы
. Начальные координаты и скорости частицы ![]() равны
равны ![]() ,
, ![]() , соответственно.
, соответственно.
Итерации в каноническом методе PSO выполняются по следующей схеме:
![]() ; (2)
; (2)
![]() . (3)
. (3)
Здесь ![]() представляет собой
представляет собой ![]() -мерный вектор псевдослучайных чисел, равномерно распределенных в интервале
-мерный вектор псевдослучайных чисел, равномерно распределенных в интервале ![]() ;
; ![]() - символ покомпонентного умножения векторов;
- символ покомпонентного умножения векторов; ![]() - вектор координат частицы
- вектор координат частицы ![]() с наилучшим (в смысле (1)) значением целевой функции
с наилучшим (в смысле (1)) значением целевой функции ![]() за все время поиска;
за все время поиска; ![]() - вектор координат соседней с данной частицы с наилучшим за время поиска значением целевой функции
- вектор координат соседней с данной частицы с наилучшим за время поиска значением целевой функции ![]() ;
; ![]() - свободные параметры алгоритма.
- свободные параметры алгоритма.
Пересчет координат частиц по формулам (2), (3) может происходить по синхронной схеме (обновление координат частиц выполняется только после определения текущих скоростей всех ![]() частиц) или по асинхронной схеме (расчет новых координат части производится до завершения указанных вычислений).
частиц) или по асинхронной схеме (расчет новых координат части производится до завершения указанных вычислений).
В процессе итераций вектор ![]() образует т.н. собственный путь (private guide) частицы
образует т.н. собственный путь (private guide) частицы ![]() , а вектор
, а вектор ![]() - локальный путь (local guide) этой частицы.
- локальный путь (local guide) этой частицы.
Свободный параметр ![]() определяет «инерционные» свойства частиц (при
определяет «инерционные» свойства частиц (при ![]() движение частиц, очевидно, замедляется). Рекомендуемое значение параметра
движение частиц, очевидно, замедляется). Рекомендуемое значение параметра ![]() равно 0.7298. В процессе оптимизации может быть эффективным постепенное уменьшение коэффициента
равно 0.7298. В процессе оптимизации может быть эффективным постепенное уменьшение коэффициента ![]() от 0.9 до 0.4. При этом большие значения параметра обеспечивают широкий обзор пространства поиска, а малые – точную локализацию минимума целевой функции. Рекомендуемые значения свободных параметров
от 0.9 до 0.4. При этом большие значения параметра обеспечивают широкий обзор пространства поиска, а малые – точную локализацию минимума целевой функции. Рекомендуемые значения свободных параметров ![]() равны 1.49618.
равны 1.49618.
Второй компонент в формуле (3) называется «когнитивным» компонентом (по социальной аналогии) и формализует тенденцию частицы вернуться в положение с минимальным значением целевой функции. Третий компонент в формуле (3) называется «социальным» компонентом. Компонент отражает влияние на данную частицу ее соседей.
Вместо формулы (3) часто используют ее вариант
![]() . (4)
. (4)
Коэффициент ![]() в этом случае называется ограничивающим фактором (restriction factor),
в этом случае называется ограничивающим фактором (restriction factor),
![]() ,
,
![]() .
.
Рекомендуемые значения параметров ![]() в этом случае равны 2.05, а их оптимальные значения определяются классом целевой функции
в этом случае равны 2.05, а их оптимальные значения определяются классом целевой функции ![]() [3].
[3].
2. Топологии соседства частиц
Эффективность метода PSO в значительной мере зависит от топологии соседства частиц (population topology, neighbourhood topology, swarm topology, sociometry). Топология соседства определяется неориентированным графом, вершины которого соответствуют частицам роя, а ребра связывают непосредственных соседей.
В вычислительной практике чаще всего используются следующие топологии соседства частиц:
-
клика (gbest-топология - глобально оптимальная топология);
-
кольцо (lbest-топология - локально оптимальная топология);
-
двумерный тор (топология фон Неймана) - двумерный тор;
-
кластерная топология.
В данной работе рассмотрены две топологии: «клика» и кластерная.
В топологии «клика» (полносвязном графе) соседями каждой из частиц ![]() ,
, ![]() являются остальные
являются остальные ![]() частицы. Диаметр полносвязного графа равен единице. Каждая частица может взаимодействовать со всеми другими частицами, и она тяготеет к лучшему решению целого роя. Частица имитирует общее оптимальное решение, поэтому её скорость зависит от информации, получаемой от всех остальных. В данном случае социальным компонентом скорости является наилучшая достигнутая позиция роя (в пространстве решений).
частицы. Диаметр полносвязного графа равен единице. Каждая частица может взаимодействовать со всеми другими частицами, и она тяготеет к лучшему решению целого роя. Частица имитирует общее оптимальное решение, поэтому её скорость зависит от информации, получаемой от всех остальных. В данном случае социальным компонентом скорости является наилучшая достигнутая позиция роя (в пространстве решений).

Рис. 1. Топология «клика»
В кластерной топологии граф имеет в качестве узлов клики из ![]() узлов. Клики числом
узлов. Клики числом ![]() объединяются в полносвязный граф, ребра которого связаны с теми узлами в кликах, степени которых равны
объединяются в полносвязный граф, ребра которого связаны с теми узлами в кликах, степени которых равны ![]() . Очевидно, что диаметр такого графа равен 3. Соседями каждой из частиц
. Очевидно, что диаметр такого графа равен 3. Соседями каждой из частиц ![]() ,
, ![]() являются
являются ![]() частиц.
частиц.

Рис. 2. Кластерная топология соседства частиц: ![]()
Диаметр графа, соответствующего используемой роем топологии соседства частиц, определяет скорость распространения информации в рое. Поэтому в рое с топологией соседства «клика» лучшее значение целевой функции, достигнутое той или иной частицей, сразу становится известным всем остальным частицам роя. В рое с кластерной топологией достигаются меньшие значения скорости распространения информации.
3. Тестовые функции
Рассмотрим основные функции, на которых проводилось тестирование данного метода оптимизации для топологий «клика» и кластерной. На рисунках 3а, 4а, 5а и 6а изображены линии уровня и траектория частиц по пути к минимуму, на рисунках 3б, 4б, 5б и 6б – вид функции в трехмерном пространстве. При построении графиков данных функций использовался Matlab 6.5.
1) Эллиптический параболоид
![]() (4.1)
(4.1)

|
а) |
б) |
|
Рис. 3. Эллиптический параболоид |
|
2) Функция Розенброка (Rosenbrock)

![]() (4.2)
(4.2)
|
а) |
б) |
|
Рис. 4. Функция Розенброка |
|
3) Функция Химмельблау (Himmelblau)
![]() (4.3)
(4.3)

|
а) |
б) |
|
Рис. 5. Функция Химмельблау |
|
4) Функция Растригина (Rastrigin)

![]() (4.4)
(4.4)
|
а) |
б) |
|
Рис. 6. Функция Растригина |
|
4. Исследование эффективности топологий
Ниже рассмотрены результаты исследования эффективности PSO-метода данных топологий для выбранных тестовых функций. Приведены таблицы вычисленных значений оптимизируемой функции при различных топологиях, построены графики сходимости функции по итерациям, а также гистограммы разброса выходных значений. В конце раздела проведен сравнительный анализ топологий на основе полученных результатов. Начальные позиции частиц генерируются случайным образом в диапазоне [-100, 100]DIM.
Таблица 1. Параметры исследования.
|
Размерность пространства |
DIM = 7 |
|
Количество частиц |
NUM = 30 |
|
Количество итераций |
TMAX = 100 |
|
Когнитивный компонент |
c1 = 1.6 |
|
Социальный компонент |
c2 = 1.6 |
|
Инерционный коэффициент |
= 0.7238 |
4.1. Результаты исследования эффективности для функции эллиптического параболоида
1) Топология «клика»
Вычисленные величины после 100 итераций:
|
Матожидание (M): |
8,14E-06 |
|
Дисперсия (D): |
1,33E-09 |
|
Суммарно: |
8,14E-06 |
Разброс значений после 100 итераций:
|
Max |
Min |
Δ |
|
3,42E-04 |
1,00E-07 |
3,42E-05 |
Здесь и далее Δ – ширина интервала при разбиении всех значений на 10 интервалов по значениям.

Рис. 7. Гистограмма достигнутых минимумов целевой функции для топологии «клика»


|
Рис. 8. Сходимость итераций для топологии «клика» (итерации 1-100) |
Рис. 9. Сходимость итераций для топологии «клика» (итерации 50-100) |
2) Кластерная топология
Вычисленные значения после 100 итераций:
|
Матожидание (M): |
5,22E-06 |
|
Дисперсия (D): |
1,41E-10 |
|
Суммарно: |
5,22E-06 |
Разброс значений после 100 итераций:
|
Max |
Min |
Δ |
|
7,65E-05 |
3,00E-08 |
7,65E-06 |

Рис. 10. Гистограмма достигнутых минимумов целевой функции для кластерной топологии

|
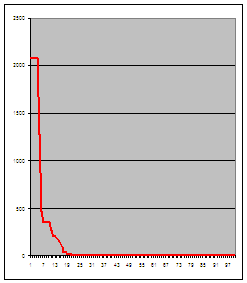
Рис. 11. Сходимость итераций для кластерной топологии (итерации 1-100) |
Рис. 12. Сходимость итераций для кластерной топологии (итерации 50-100) |
Для эллиптического параболоида более эффективной оказалась кластерная топология: Σ=5,22E-06, для топологии «клика» Σ=8,14E-06. Разброс значений незначительный (см. Рис. 7, 10)
4.2. Результаты исследования эффективности для функции Розенброка
1) Топология «клика»
Вычисленные величины после 100 итераций:
|
Матожидание (M): |
0,676434 |
|
Дисперсия (D): |
11,8939 |
|
Суммарно: |
12,57033 |
Разброс значений после 100 итераций:
|
Max |
Min |
Δ |
|
25,7831 |
0 |
2,57831 |

Рис. 13. Гистограмма достигнутых минимумов целевой функции для топологии «клика»


|
Рис. 14. Сходимость итераций для топологии «клика» (итерации 1-100) |
Рис. 15. Сходимость итераций для топологии «клика» (итерации 18-100) |
2) Кластерная топология
Вычисленные значения после 100 итераций:
|
Матожидание (M): |
0,336689 |
|
Дисперсия (D): |
2,675064 |
|
Суммарно: |
3,011753 |
Разброс значений после 100 итераций:
|
Max |
Min |
Δ |
|
16,0535 |
0 |
1,60535 |

Рис. 16. Гистограмма достигнутых минимумов целевой функции для кластерной топологии


|
Рис. 17. Сходимость итераций для кластерной топологии (итерации 1-100) |
Рис. 18. Сходимость итераций для кластерной топологии (итерации 18-100) |
Для функции Розенброка более эффективной оказалась кластерная топология: Σ=3,011753, для «клики» Σ=12,57033. Разброс значений незначительный (см. Рис. 13, 16)
4.3. Результаты исследования эффективности для функции Химмельблау
1) Топология «клика»
Вычисленные величины после 100 итераций:
|
Матожидание (M): |
2,84E-12 |
|
Дисперсия (D): |
2,4E-23 |
|
Суммарно: |
2,84E-12 |
Разброс значений после 100 итераций:
|
Max |
Min |
Δ |
|
2,401E-11 |
0 |
2,4E-12 |

Рис. 19. Гистограмма достигнутых минимумов целевой функции для топологии «клика»
 Рис. 20. Сходимость итераций для топологии «клика» (итерации 1-100)
Рис. 20. Сходимость итераций для топологии «клика» (итерации 1-100)
2) Кластерная топология
Вычисленные значения после 100 итераций:
|
Матожидание (M): |
9,17E-12 |
|
Дисперсия (D): |
2,92E-21 |
|
Суммарно: |
9,17E-12 |
Разброс значений после 100 итераций:
|
Max |
Min |
Δ |
|
4,41E-10 |
0 |
4,406E-11 |

Рис. 21. Гистограмма достигнутых минимумов целевой функции для кластерной топологии

Рис. 22. Сходимость итераций для кластерной топологии (итерации 1-100)
Для функции Химмельблау более эффективной оказалась топология «клика»: Σ=2,84E-12, для кластерной Σ=9,17E-12. Разброс значений незначительный (см. Рис. 19, 21)
4.4. Результаты исследования эффективности для функции Растригина
1) Топология «клика»
Вычисленные величины после 100 итераций:
|
Матожидание (M): |
1,292622 |
|
Дисперсия (D): |
1,45901 |
|
Суммарно: |
2,751632 |
Разброс значений после 100 итераций:
|
Max |
Min |
Δ |
|
4,9748 |
0 |
0,49748 |

Рис. 23. Гистограмма достигнутых минимумов целевой функции для топологии «клика»


|
Рис. 24. Сходимость итераций для топологии «клика» (итерации 1-100) |
Рис. 25. Сходимость итераций для топологии «клика» (итерации 50-100) |
2) Кластерная топология
Вычисленные значения после 100 итераций:
|
Матожидание (M): |
1,076358 |
|
Дисперсия (D): |
0,885007 |
|
Суммарно: |
1,961365 |
Разброс значений после 100 итераций:
|
Max |
Min |
Δ |
|
3,9798 |
0 |
0,39798 |

Рис. 26. Гистограмма достигнутых минимумов целевой функции для кластерной топологии


|
Рис. 27. Сходимость итераций для кластерной топологии (итерации 1-100) |
Рис. 28. Сходимость итераций для кластерной топологии (итерации 50-100) |
Для функции Растригина более эффективной оказалась кластерная топология: Σ=1,961365, для «клики» Σ=2,751632. В данном случае разброс значений существенный (см. Рис. 23, 26), для «клики» дисперсия вносит основной вклад в общую сумму (D=1,45901)
4.5. Анализ результатов
Сравнение оптимизационных свойств метода PSO проводилось по сумме матожидания и дисперсии для достигнутого значения минимума заданной функции. Для эллиптического параболоида и функции Химмельблау обе топологии обеспечивают очень хорошую сходимость (порядка 10-6 и 10-12 соответственно) и малый разброс значений (см. Рис. 7, 10, 19, 21). Стоит отметить, что для функции Химмельблау оптимизация проводилось при размерности пространства DIM = 2 (см. формулу 4.3), что и явилось причиной столь хорошей сходимости (Σ=2,8410-12)
Для канонического метода PSO функции Розенброка и Растригина слишком сложны, и для обеих топологий при заданных начальных условиях достигается плохая сходимость (порядка 103), поэтому для данных функций была принята размерность пространства DIM = 3 без изменения других параметров.
Для функции Розенброка более эффективной оказалась кластерная топология (Σ=3,011753), в то время как для клики Σ=12,57033. Это наглядно показано на графиках сходимости итераций (см. Рис. 15, 18). Наконец, для функции Растригина также лучше оказалась кластерная топология (Σ=1,961365), в то время как для клики Σ=2,751632. Видно, что в данном случае разброс значений уже существенный в обоих случаях (см. Рис. 23, 26). При использовании топологии «клика» функция чаще попадает в локальный минимум, один из которых изображен на соответствующем графике сходимости для итераций 50-100 (см. Рис. 25)
Заключение
На основании результатов можно сделать выводы:
-
из-за большей степени связности частиц между собой (топология «клика») PSO-метод сходится быстрее; однако быстрая сходимость ведёт к менее тщательному исследованию пространства решений;
-
при использовании кластерной топологии PSO-метода шанс попасть в локальный минимум и найти, таким образом, только субоптимальное решение меньше; c другой стороны, данный метод работает медленнее, чем при использовании топологии «клика»
Список литературы
1. Субботин С.А., Олейник Ан.А., Олейник Ал.А. (2006) PSO-метод. //«Интеллектуальные мультиагентные методы (Swarm Intelligence)» – Ч.3 – С.55-70.
2. Карпенко А.П., Селиверстов Е.Ю. (2008) «Обзор методов роя частиц (PSO) для задачи глобальной оптимизации» // Наука и образование: электронное научно-техническое издание, www.technomag.edu.ru, март, 2009.
3. J. Kennedy, R. Eberhart (1995) Particle swarm optimization. // Proceedings of IEEE International conference on Neural Networks. – 1995, pp. 1942 - 1948.
4. Marco Doringo et al. (2008) Particle swarm optimization. // Scholarpedia, 3(11):1486.
5. J. Kennedy. Stereotyping: improving particle swarm performance with cluster analysis. // Proceedings of the 2000 Congress on Evolutionary Computation. - 2002, v.2, pp. 1507—1512.
6. R. Mendes, Member, IEEE, J. Kennedy and J. Neves. The Fully Informed Particle Swarm: Simpler, Maybe Better. // IEEE Transactions of Evolutionary Computation, vol. 1, no. 1, January 2025.
7. C. Zhang, H. Shao, Y. Li. Particle swarm optimization for evolving artificial network. //Proceedings of IEEE International Conference on System, Man and Cybernetics, 2000, pp. 2487-2490.
Публикации с ключевыми словами: глобальная оптимизация, метод роя частиц, метод PSO
Публикации со словами: глобальная оптимизация, метод роя частиц, метод PSO
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



