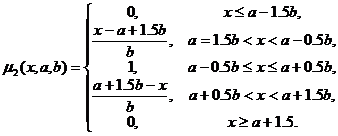научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#4 2008
DOI: 10.7463/0408.0086335
УДК 519.6
Карпенко А.П. (д.ф.-м.наук, профессор МГТУ им.Н.Э.Баумана,
телефон: 263-65-26,
E-mail: karpenko@nog.ru)
Федорук В.Г. (к.т.н., доцент МГТУ им.Н.Э.Баумана,
телефон: 263-65-26,
E-mail: fedoruk@comcor.ru)
Работа является третьей работой в серии, посвященной адаптивным методам решения непрерывной конечномерной задачи многомерной многокритериальной оптимизации [1, 2]. Рассматривается три метода аппроксимации функции предпочтений лица, принимающего решения (ЛПР) - метод на основе персептронных нейронных сетей, метод на основе нейронных сетей с радиальными базисными функциями и метод на основе нечеткой логики.
1. Основные обозначения
Постановка задачи многокритериальной оптимизации приведена в первой работе рассматриваемой серии [1]. Повторим основные обозначения, введенные там.
Вектор ![]() - n-мерный вектор параметров задачи (вектор варьируемых параметров), где
- n-мерный вектор параметров задачи (вектор варьируемых параметров), где
![]() -
-
замкнутое множество допустимых значений вектора параметров; ![]() - ограничивающие функции.
- ограничивающие функции.
![]() - векторный критерий оптимальности, определенный на множестве
- векторный критерий оптимальности, определенный на множестве ![]() . ЛПР, полагается, стремится минимизировать каждый из частных критериев
. ЛПР, полагается, стремится минимизировать каждый из частных критериев ![]() .
.
Полагается, что все частные критерии тем или иным способом нормализованы и за нормализованными частными критериями оптимальности сохранены обозначения ![]() .
.
Решение задачи многокритериальной оптимизации отыскивается с помощью метода скалярной сверки, который при каждом фиксированном векторе ![]() сводит решение задачи многокритериальной оптимизации к решению однокритериальной задачи глобальной условной оптимизации
сводит решение задачи многокритериальной оптимизации к решению однокритериальной задачи глобальной условной оптимизации
![]() , (1)
, (1)
где ![]() - результат операции свертки (суперкритерий),
- результат операции свертки (суперкритерий), ![]()
![]() - вектор весовых множителей,
- вектор весовых множителей, ![]() - множество допустимых значений этого вектора.
- множество допустимых значений этого вектора.
Если при каждом ![]() решение задачи (1) единственно, то условие (1) ставит в соответствие каждому из допустимых векторов
решение задачи (1) единственно, то условие (1) ставит в соответствие каждому из допустимых векторов ![]() единственный вектор
единственный вектор ![]() и соответствующие значения частных критериев оптимальности
и соответствующие значения частных критериев оптимальности ![]() . Это обстоятельство позволяет полагать, что функция предпочтения ЛПР
. Это обстоятельство позволяет полагать, что функция предпочтения ЛПР ![]() определена не на множестве
определена не на множестве ![]() , а на множестве
, а на множестве ![]() :
:
![]() .
.
В результате задача многокритериальной оптимизации сводится к задаче выбора вектора ![]() такого, что
такого, что
![]() . (2)
. (2)
Величина ![]() полагается лингвистической переменной со значениями ”Очень-очень плохо”, ”Очень плохо”, …, ”Отлично”. Центры соответствующих нечетких множеств обозначаются
полагается лингвистической переменной со значениями ”Очень-очень плохо”, ”Очень плохо”, …, ”Отлично”. Центры соответствующих нечетких множеств обозначаются ![]() и имеют четкие значения 1, 2, …, 9, соответственно.
и имеют четкие значения 1, 2, …, 9, соответственно.
При аппроксимации функции предпочтений ЛПР с помощью нейронных сетей вместо задачи (2) рассматривается задача отыскания вектора ![]() , обеспечивающего максимальное значение четкой дискретной функции
, обеспечивающего максимальное значение четкой дискретной функции ![]() :
:
![]() . (3)
. (3)
2. Нейронные сети и их аппроксимационные свойства
Искусственный нейрон (далее - нейрон) обычно определяется как элемент, имеющий некоторое количество входов (синапсов), на которые поступают входные сигналы ![]() и один выход (аксон), с которого снимается выходной сигнал
и один выход (аксон), с которого снимается выходной сигнал ![]() (см. Рис. 1).
(см. Рис. 1).
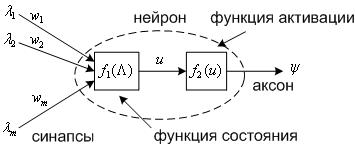
Рис. 1. К определению искусственного нейрона.
Функция состояния нейрона ![]() определяет состояние нейрона в зависимости от его входов, весов входов
определяет состояние нейрона в зависимости от его входов, весов входов ![]() и, возможно, предыдущих состояний нейрона. Чаще всего используют следующие функции состояния, не зависящие от предыдущего состояния [3].
и, возможно, предыдущих состояний нейрона. Чаще всего используют следующие функции состояния, не зависящие от предыдущего состояния [3].
1. Скалярное произведение векторов ![]()
![]() , (4)
, (4)
2. Расстояние между векторами ![]() в некоторой метрике, например,
в некоторой метрике, например,
![]() , (5)
, (5)
где ![]() - положение центра функции
- положение центра функции ![]() .
.
Искусственный нейрон с функцией состояния (4) называется персептроном, с функцией состояния (2) – нейроном с радиальной базисной функцией.
На функцию активации (передаточную функцию) ![]() обычно налагается ограничение
обычно налагается ограничение ![]() . В качестве
. В качестве ![]() могут использоваться различные функции. Чаще других используют сигмоидальную функцию активации
могут использоваться различные функции. Чаще других используют сигмоидальную функцию активации
![]() ,
,
где a - параметр, определяющий фронт этой функции. Отметим, что в данном случае ее производная имеет вид ![]() .
.
Часто функция состояния и функция активации объединяются в одну (передаточную) функцию. Далее мы будем следовать этому соглашению.
Нейронные сети образуются путем соединения входов одних нейронов с выходами других. Как правило, вид передаточных функций всех нейронов в сети фиксирован (используются однородные сети), а веса и, возможно, параметры передаточных функций могут изменяться.
Существует нейронные сети с множеством различных топологий. Основными являются многослойные сети, которые классифицируются следующим образом:
· сети без обратных связей (сети прямого распространения) - многослойные персептроны и многослойные сети с радиальными базисными функциями;
· сети с обратными связями (рекуррентные сети) - соревновательные сети, сети Кохонена, сети Хопфилда, сети Элмана, сети Жордана и пр.
Для решения задач аппроксимации наиболее адекватными являются многослойные сети прямого распространения - двухмерные многослойные персептроны (MultiLayer Perceptron, MLP-сети) и двухмерные нейронные сети, использующие радиальные базисные функции (RadialBasisFunctionNetwork, RBF-сети). Если, как в нашем случае, аппроксимируемая функция является скалярной, то минимальной реализацией таких сетей является двухслойная нейронная сеть, состоящая из входного (распределительного), промежуточного (скрытого) и выходного слоя из одного нейрона (при подсчете числа слоев входной слой обычно не учитывается) - см. Рис. 2.
Задачу аппроксимации скалярной функции можно интерпретировать как задачу реализации отображения ![]() , которое формирует «правильный» выход
, которое формирует «правильный» выход ![]() при любом возможном векторе входов
при любом возможном векторе входов ![]() . Отображение должно быть построено на основе «обучающей выборки» - конечного набора пар (<Вход>, <Известный выход>). После обучения нейронная сеть должна обеспечить правильное формирование выходов, как для обучающей выборки, так (в пределе) и для любых других возможных входов.
. Отображение должно быть построено на основе «обучающей выборки» - конечного набора пар (<Вход>, <Известный выход>). После обучения нейронная сеть должна обеспечить правильное формирование выходов, как для обучающей выборки, так (в пределе) и для любых других возможных входов.
Теорема 1 (теорема о полноте). Если множество ![]() - замкнуто и ограничено, а функция
- замкнуто и ограничено, а функция ![]() принадлежит классу
принадлежит классу ![]() скалярных непрерывных на множестве
скалярных непрерывных на множестве ![]() функций, то эта функция может быть равномерно приближена функцией, вычислимой с помощью нейросети [4].
функций, то эта функция может быть равномерно приближена функцией, вычислимой с помощью нейросети [4].

Рис. 2. Двухслойная сеть без обратных связей: ![]() - количество нейронов
- количество нейронов ![]() во входном слое;
во входном слое; ![]() - количество нейронов
- количество нейронов ![]() в скрытом слое.
в скрытом слое.
3. Аппроксимация функции предпочтений на основе персептронной нейронной сети
Обозначим выходы нейронов скрытого слоя ![]() . Тогда формально функционирование MLP-нейронной сети, представленной на Рис. 2, описывается как суперпозиция функций
. Тогда формально функционирование MLP-нейронной сети, представленной на Рис. 2, описывается как суперпозиция функций
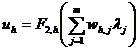 ,
, ![]() ,
, ![]() .
.
Здесь ![]() ,
, ![]() - передаточные функции нейронов
- передаточные функции нейронов ![]() ,
, ![]() , соответственно.
, соответственно.
Точным решением рассматриваемой задачи аппроксимации является функция ![]() , заданная своими значениями на обучающей выборке
, заданная своими значениями на обучающей выборке ![]() ,
, ![]() . Будем полагать, что примеры из обучающей выборки упорядочены по времени их получения: пример
. Будем полагать, что примеры из обучающей выборки упорядочены по времени их получения: пример ![]() получен в результате первого опыта, пример
получен в результате первого опыта, пример ![]() - в результате второго опыта и т.д.
- в результате второго опыта и т.д.
В качестве оценки ошибки ![]() MLP-сети при обработке вектора
MLP-сети при обработке вектора ![]() используем величину
используем величину 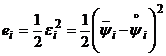 , а в качестве оценки ошибки сети при обработке всех Nвекторов из обучающей выборки - среднеквадратичное отклонение (критерий максимального правдоподобия)
, а в качестве оценки ошибки сети при обработке всех Nвекторов из обучающей выборки - среднеквадратичное отклонение (критерий максимального правдоподобия) 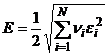 , где
, где ![]() - весовой множитель i-го примера из обучающей выборки.
- весовой множитель i-го примера из обучающей выборки.
В качестве множителей ![]() предлагается использовать величину
предлагается использовать величину ![]() , где
, где ![]() - свободный параметр. Назовем это правило определения весовых множителей
- свободный параметр. Назовем это правило определения весовых множителей ![]() правилом экспоненциального возрастания весов опытов. Правило формализует повышение точности оценок лицом, принимающим решения, значений своей функции предпочтений по мере увеличения количества опытов и лучшего понимания им решаемой задачи многокритериальной оптимизации.
правилом экспоненциального возрастания весов опытов. Правило формализует повышение точности оценок лицом, принимающим решения, значений своей функции предпочтений по мере увеличения количества опытов и лучшего понимания им решаемой задачи многокритериальной оптимизации.
Заметим, что другой класс критериев качества обучения для задач аппроксимации образуют робастные целевые функции и функции с возможностью задания допуска на точность решения задачи [5].
Для первоначальной оценки числа нейронов Hв скрытом слое MLP-сети можно использовать эвристическую рекомендацию [6]:
![]() . (6)
. (6)
В нашем случае величина ![]() в этой формуле находится из условия
в этой формуле находится из условия
![]() . (7)
. (7)
Отметим, что оценка (6), (7) исходит из предположения об использовании в MLP-сети сигмоидальных передаточных функций.
Для определения числа нейронов в скрытом слое MLP-сети чаще всего используют метод динамического наращивания узлов, суть которого состоит в следующем. Если средняя скорость уменьшения ошибки ![]() становится ниже некоторой величины
становится ниже некоторой величины ![]() , то в скрытый слой добавляется один нейрон, подключенный ко всем входным нейронам и выходному нейрону. Здесь
, то в скрытый слой добавляется один нейрон, подключенный ко всем входным нейронам и выходному нейрону. Здесь
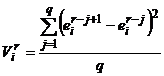 ,
,
r– номер обучающей итерации, на которой производится оценка скорости обучения, q– количество итераций.
Известно значительное количество различных модификаций метода динамического наращивания узлов. Например, качество обучения можно повысить за счет использования нескольких нейронов-кандидатов, претендующих на включение в сеть. Эффективность включения в сеть каждого из этих нейронов проверяется по отдельности (путем обучения сети с каждым из них и сравнения достигнутой точности аппроксимации).
При фиксированном количестве нейронов в скрытом слое задача обучения MLP-сети состоит в определении весов ![]() ,
, ![]() ,
, ![]() и для сети с сигмоидальными передаточными функциями чаще всего решается с использованием алгоритма обратного распространения (backpropagation), который включает в себя три этапа: прямой ход; обратный ход; градиентный шаг.
и для сети с сигмоидальными передаточными функциями чаще всего решается с использованием алгоритма обратного распространения (backpropagation), который включает в себя три этапа: прямой ход; обратный ход; градиентный шаг.
Легко видеть, что
 ,
, ![]() ,
,
где ![]() - производная передаточной функции нейрона
- производная передаточной функции нейрона ![]() при обработке вектора
при обработке вектора ![]() ,
, ![]() - соответствующая ошибка сети в скрытом слое,
- соответствующая ошибка сети в скрытом слое, ![]() .
.
Имея указанные производные, легко найти градиент величины ![]() по весам
по весам ![]() ,
, ![]() :
:
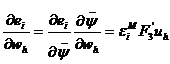 ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Таким образом, для каждого ![]() прямой ход алгоритма обратного распространения включает в себя следующие вычисления:
прямой ход алгоритма обратного распространения включает в себя следующие вычисления:
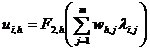 ,
, ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
На обратном ходе вычисляются величины
![]() ,
, ![]() ,
, ![]() .
.
Наконец, градиентный шаг метода обратного распространения имеет вид:
![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() .
.
Здесь ![]() - величина шага в направлении антиградиента.
- величина шага в направлении антиградиента.
Хорошо известно, что метод обратного распространения не свободен от существенных недостатков:
· метод не всегда сходится;
· процесс градиентного спуска может завершиться в одном из локальных минимумов критерия качества обучения;
· при увеличении количества нейронов в скрытом слое MLP-сеть склонна к переобучению;
· в MLP-сети с функциями активации, имеющими горизонтальные асимптоты (например, с сигмоидальными функциями), в процессе обучения может иметь место «паралич» сети.
Для улучшения сходимости алгоритма обратного распространения могут быть предприняты следующие меры [7 - 10].
1). Выбор начального приближения для весов таким образом, чтобы гарантированно обеспечить попадание значений скалярных произведений в «рабочую зону» передаточных функций. Можно, например, использовать в качестве начальных значений весов значения
![]() ,
, ![]() ,
,
где ![]() ,
, ![]() .
.
2). Добавление в формулу для приращения веса некоторой инерционности. Например, можно принять ![]() , где
, где ![]() - коэффициент инерционности, r– номер текущей итерации.
- коэффициент инерционности, r– номер текущей итерации.
3). Ограничение возможного роста абсолютных значений весов путем добавления к функционалу ![]() штрафного слагаемого:
штрафного слагаемого:
![]() ,
, ![]() .
.
Отметим, что такое «сокращение весов» представляет собой частный случай регуляризации некорректно поставленных задач по А. Н. Тихонову. Важно, что данный прием повышает устойчивость весов в случае мультиколлинеарности - когда в обучающей выборке имеются линейно зависимые или сильно коррелированные векторы![]() .
.
4). Усреднение градиента по всем или некоторой части примеров обучающей выборки – использование «пакетной коррекции».
5). Применение более сложных алгоритмов выбора величины шага, например, градиентного алгоритма с дроблением шага, алгоритма наискорейшего спуска, алгоритма на основе квадратичной аппроксимации функции ![]() ,
, ![]() и т.д.
и т.д.
6). Использование комбинации градиентного метода с методом случайного локального поиска с целью обеспечения поиска глобального минимума функционала ![]() ,
, ![]() - метод «потряхивания весов».
- метод «потряхивания весов».
7). Использование методов и алгоритмов оптимизации, обеспечивающих более высокую скорость сходимости - метод сопряженных градиентов, квази-ньютоновский метод, алгоритмы QuickProp, RProp.
Эффективность обучения можно повысить также за счет выбора критерия останова, изменения порядка предъявления объектов обучающей выборки, использования «раннего останова», обучения с использованием генетических и «отжиговых» алгоритмов обучения и пр. [7].
4. Аппроксимация функции предпочтений на основе нейронной сети с радиальными базисными функциями
Отметим прежде следующее обстоятельство. Из теоремы 1 следует, что MLP-сети и RBF-сети являются универсальными аппроксиматорами. Поэтому всегда существует RBF-сеть, имитирующая любую MLP-сеть, и наоборот.
RBF-сеть аппроксимирует произвольную нелинейную функцию с помощью всего одного промежуточного слоя (см. Рис. 2). Таким образом, в отличие от MLP-сети в данном случае отсутствует проблема определения количества слоев в сети. Выходной слой RBF-сети строится на основе нейрона с линейной передаточной функцией, что позволяет не обучать этот нейрон. Известным недостатком RBF-сетей являются их плохие экстраполяционные свойства [11].
Рассмотрим типичную для наших приложений ситуацию, когда число элементов в обучающей выборке относительно невелико (не превышает нескольких сотен). При этом каждому вектору ![]() можно поставить в соответствие свой нейрон с центром в точке
можно поставить в соответствие свой нейрон с центром в точке ![]() , т.е. можно положить
, т.е. можно положить ![]() . Таким образом, в данном случае RBF-сеть содержит в скрытом слое N нейронов, веса
. Таким образом, в данном случае RBF-сеть содержит в скрытом слое N нейронов, веса ![]() которых равны единице. Функционирование RBF-сети при этом описывается формулами
которых равны единице. Функционирование RBF-сети при этом описывается формулами
![]()
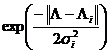 ,
, ![]() ,
,
![]()
![]() . (8)
. (8)
Здесь ![]() ,
, ![]() - параметр, определяющий ширину колокола функции
- параметр, определяющий ширину колокола функции ![]() .
.
Если предположить, что величины ![]() ,
, ![]() фиксированы, то задача нахождения весов в формуле (8) сводится к решению системы линейных алгебраических уравнений (СЛАУ)
фиксированы, то задача нахождения весов в формуле (8) сводится к решению системы линейных алгебраических уравнений (СЛАУ)
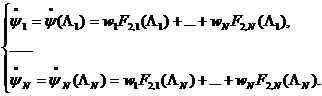 (9)
(9)
Здесь, как и ранее, ![]() - требуемый выход нейронной сети, соответствующий входному вектору
- требуемый выход нейронной сети, соответствующий входному вектору ![]() ,
, ![]() .
.
Решение указанной СЛАУ сводится к обращению ![]() матрицы
матрицы
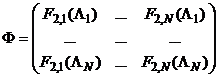 .
.
Теорема 2 (теорема Митчела). Если в обучающей выборке ![]() ,
, ![]() нет совпадающих точек, то матрица
нет совпадающих точек, то матрица ![]() является невырожденной [3].
является невырожденной [3].
В случае ![]() матрица
матрица ![]() может быть плохо обусловленной. Поэтому, вообще говоря, требуется регуляризация СЛАУ (9).
может быть плохо обусловленной. Поэтому, вообще говоря, требуется регуляризация СЛАУ (9).
Как и в MLP-сети, в качестве оценки ошибки используем взвешенное среднеквадратичное отклонение ![]() , где, напомним,
, где, напомним, ![]() - весовой множитель i-го примера обучающей выборки, значение которого определяется правилом экспоненциального возрастания весов (см. раздел 3),
- весовой множитель i-го примера обучающей выборки, значение которого определяется правилом экспоненциального возрастания весов (см. раздел 3), ![]() .
.
Очевидно, что если веса ![]() определены, то при любых параметрах
определены, то при любых параметрах ![]() на указанной обучающей выборке ошибка
на указанной обучающей выборке ошибка ![]() . Поэтому для определения величин
. Поэтому для определения величин ![]() необходима еще одна обучающая выборка
необходима еще одна обучающая выборка ![]() ,
, ![]() ,
, ![]() . Тогда задача определения оптимальных значений величин
. Тогда задача определения оптимальных значений величин ![]() может быть записана в виде
может быть записана в виде
![]() . (10)
. (10)
Задача (10) представляет собой многомерную задачу условной оптимизации и решать ее приходится с использованием итеративных численных методов оптимизации.
Найдем частные производные критерия ![]() по переменной
по переменной ![]() ,
, ![]() :
:
 ;
;
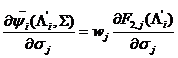 ;
;
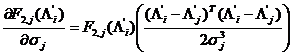 .
.
Таким образом,
 .
.
Заметим, что поскольку  , в последней сумме j-е слагаемое также равно нулю.
, в последней сумме j-е слагаемое также равно нулю.
Таким образом, при фиксированных весах ![]() для решения задачи (10) можно использовать, например, метод проекции градиента, комбинацию метода штрафных функций с градиентным методом и т.д. [8].
для решения задачи (10) можно использовать, например, метод проекции градиента, комбинацию метода штрафных функций с градиентным методом и т.д. [8].
При использовании градиентного метода с дроблением шага итерационная формула имеет вид
![]() ,
,
где ![]() - текущий шаг (начальный шаг является свободным параметром метода),
- текущий шаг (начальный шаг является свободным параметром метода), ![]() - вектор градиента с компонентами
- вектор градиента с компонентами ![]() ,
, ![]() . Скорость обучения можно существенно повысить, если в этом процессе использовать квадратичную аппроксимацию функции
. Скорость обучения можно существенно повысить, если в этом процессе использовать квадратичную аппроксимацию функции ![]() .
.
Поскольку критерий ![]() может быть многоэкстремальным, задачу (10) следует решать многократно, исходя из разных начальных значений компонентов вектора
может быть многоэкстремальным, задачу (10) следует решать многократно, исходя из разных начальных значений компонентов вектора ![]() .
.
Отметим, что при высокой размерности обучающей выборки целесообразно использовать не градиентные методы, а методы на основе генетических алгоритмов оптимизации.
Замечание. Рассмотренная схема обучения (когда количество нейронов в скрытом слое равно количеству примеров в первой обучающей выборке) не применима в случае, когда эта выборка содержит слишком большое количество элементов (тысячи или десятки тысяч). В таком случае приходится группировать элементы обучающего множества по степени их близости в пространстве входных значений в некоторое число кластеров. Количество таких кластеров задает количество нейронов в скрытом слое сети, а их средние характеристики используют для начальной инициализации параметров передаточных функций. Для такого рода группировки можно использовать метод k-средних, самоорганизующиеся карты Кохонена или деревья решений.
5. Основные понятия нечеткой логики
Теоретической основой аппроксимации функций с помощью аппарата нечетких множеств является следующая теорема.
Теорема 3 (теорема Ванга). Для любой вещественной непрерывной функции ![]() , заданной на компакте
, заданной на компакте ![]() и для произвольного
и для произвольного ![]() существует нечеткая экспертная система, формирующая выходную функцию
существует нечеткая экспертная система, формирующая выходную функцию ![]() такую, что
такую, что
 ,
,
где ![]() - некоторая функциональная норма [12].
- некоторая функциональная норма [12].
Если ![]() - некоторое универсальное множество, то нечеткое множество
- некоторое универсальное множество, то нечеткое множество ![]() представляет собой набор пар (синглтонов)
представляет собой набор пар (синглтонов) ![]() , где
, где ![]() и
и ![]() - функция принадлежности, представляющая собой некоторую субъективную меру принадлежности элемента
- функция принадлежности, представляющая собой некоторую субъективную меру принадлежности элемента ![]() нечеткому множеству
нечеткому множеству ![]() . Функция принадлежности
. Функция принадлежности ![]() может принимать значения от нуля (абсолютная не принадлежность элемента
может принимать значения от нуля (абсолютная не принадлежность элемента ![]() нечеткому множеству
нечеткому множеству ![]() ) до единицы (абсолютная принадлежность). В случае непрерывного множества
) до единицы (абсолютная принадлежность). В случае непрерывного множества ![]() используют обозначение
используют обозначение
 .
.
Этап построения нечеткой модели, на котором определяются терм-множества переменных и необходимые для их формализации функции принадлежности, называется фаззификации переменных (fuzzification).
При выполнении логической операции «И» над нечеткими множествами используется T-норма, а при выполнении логической операции «ИЛИ» - S-норма [13].
Чаще всего используют следующие T-нормы: пересечение по Л.Заде - ![]() ; вероятностное пересечение -
; вероятностное пересечение - ![]() ; пересечение по Лукасевичу -
; пересечение по Лукасевичу - ![]() . Если
. Если ![]() - нечеткие множества с функциями принадлежности
- нечеткие множества с функциями принадлежности ![]() , соответственно, то для пересечения по Л.Заде
, соответственно, то для пересечения по Л.Заде ![]() , для вероятностного пересечения
, для вероятностного пересечения ![]() и для пересечения по Лукасевичу
и для пересечения по Лукасевичу ![]() .
.
В качестве S-норм обычно используют объединение по Л. Заде - ![]() , вероятностное объединение -
, вероятностное объединение - ![]() , объединение по Лукасевичу -
, объединение по Лукасевичу - ![]() . Аналогично Т-нормам функция принадлежности нечеткого множества
. Аналогично Т-нормам функция принадлежности нечеткого множества ![]() равна
равна ![]() , множества
, множества ![]() -
- ![]() и множества
и множества ![]() -
- ![]() .
.
Дефаззификацией (defuzzification) называется процедура преобразования нечеткого множества в четкое число. Простейшим способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности. Для многоэкстремальных функций принадлежности используются следующие методы дефаззификации:
· метод центра тяжести (centroid), при котором искомое четкое число a находится из равенства
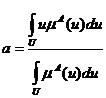 ;
;
· метод медианы (bisector), при котором число aпредставляет собой точку на оси абсцисс, перпендикуляр в которой к этой оси делит площадь под кривой функции принадлежности на две равные части
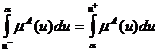 ;
;
· метод максимума (MeanOfMaximumsMOM), в котором четкое число a находится из равенства
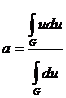 ,
,
где G - множество всех элементов из U, имеющих максимальную степень принадлежности нечеткому множеству A.
Нечетким логическим выводом (fuzzylogicinference) называется аппроксимация зависимости ![]() с помощью нечеткой базы знаний и операций над нечеткими множествами. Основу нечеткого логического вывода составляет [13]
с помощью нечеткой базы знаний и операций над нечеткими множествами. Основу нечеткого логического вывода составляет [13]
Композиционное правило Заде. Если ![]() - известное нечеткое отношение между вектором входов
- известное нечеткое отношение между вектором входов ![]() и выходной переменной
и выходной переменной ![]() , то при нечетком значении входной переменной
, то при нечетком значении входной переменной ![]() , нечеткое значения выходной переменной определяется как
, нечеткое значения выходной переменной определяется как ![]() , где
, где ![]() - символ максиминой композиции.
- символ максиминой композиции.
Различают нечеткий логический вывод [13]
· на основе синглтонной модели нечеткого вывода,
· по алгоритму Сугено (нечеткий логический вывод Сугено),
· по алгоритму Мамдани (нечеткий логический вывод Мамдани).
Синглтонная модель нечеткого вывода предполагает, что входы объекта ![]() являются нечеткими множествами, а выход объекта
являются нечеткими множествами, а выход объекта ![]() задается четким числом. В наших условиях принципиальной является нечеткость выхода. Поэтому синглтонная модель далее не рассматривается.
задается четким числом. В наших условиях принципиальной является нечеткость выхода. Поэтому синглтонная модель далее не рассматривается.
Нечеткий логический вывод Сугено исходит из того, что задано некоторое количество линейных функций ![]() ,
, ![]() . Границы подобластей пространства входов
. Границы подобластей пространства входов ![]() , в которых действует та или иная линейная зависимость, полагаются размытыми, так что в одной подобласти может выполняться одновременно, но в разной степени, несколько зависимостей. Мы не видим возможности содержательно формализовать нашу задачу в таких терминах. Поэтому алгоритм Сугено далее не рассматривается. Таким образом, рассматривается только нечеткий логический вывод Мамдани.
, в которых действует та или иная линейная зависимость, полагаются размытыми, так что в одной подобласти может выполняться одновременно, но в разной степени, несколько зависимостей. Мы не видим возможности содержательно формализовать нашу задачу в таких терминах. Поэтому алгоритм Сугено далее не рассматривается. Таким образом, рассматривается только нечеткий логический вывод Мамдани.
Одним из центральных вопросов теории нечетких множеств является вопрос о построении функций принадлежности. В практических приложениях применяются методы определения функций принадлежности по выборкам и на основании априорной информации, в которую входят ограничения на эти функции [14].
Мы будем рассматривать в качестве функции принадлежности следующие двухпараметрические функции ![]() , где первый параметр aопределяет положение оси симметрии функции (а если функция унимодальная, то и положение ее максимума), а второй b– ширину ее колокола.
, где первый параметр aопределяет положение оси симметрии функции (а если функция унимодальная, то и положение ее максимума), а второй b– ширину ее колокола.
1). Треугольная функция принадлежности
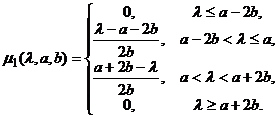
2). Трапецеидальная функция принадлежности
|
3). Гауссова функция принадлежности 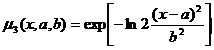
4). Колоколообразная функция принадлежности  .
.
Для любой указанных функций принадлежности ![]() будем полагать
будем полагать ![]() ,
, ![]() ,
, ![]() . Аналогично, для любой функции принадлежности
. Аналогично, для любой функции принадлежности ![]() будем полагать
будем полагать ![]() , а
, а ![]() ,
, ![]() ,
, ![]() . Отметим, что такое соглашение допускает использование функций принадлежности с разной шириной колокола для разных частных критериев оптимальности. Большая ширина колокола могла бы означать большую важность соответствующего частного критерия оптимальности. Однако относительная важность критериев учитывается в весах этих критериев. Поэтому будем полагать, что для каждой текущей базы знаний ширина всех функций принадлежности
. Отметим, что такое соглашение допускает использование функций принадлежности с разной шириной колокола для разных частных критериев оптимальности. Большая ширина колокола могла бы означать большую важность соответствующего частного критерия оптимальности. Однако относительная важность критериев учитывается в весах этих критериев. Поэтому будем полагать, что для каждой текущей базы знаний ширина всех функций принадлежности ![]() одинакова.
одинакова.
6. Аппроксимация функции предпочтений на основе нечеткой логики
Задачу аппроксимации функции предпочтений ЛПР можно рассматривать как задачу идентификации объекта, в котором входными переменными являются значения весов частных критериев оптимальности – нечеткие термы ![]()
![]() ,
, ![]() , а выходной переменной, формализующей предпочтения ЛПР, является лингвистическая переменная
, а выходной переменной, формализующей предпочтения ЛПР, является лингвистическая переменная ![]() со значениями из лингвистического терм-множества
со значениями из лингвистического терм-множества ![]() . Здесь
. Здесь ![]() «очень плохо»,
«очень плохо», ![]() «плохо»,
«плохо», ![]() «удовлетворительно»,
«удовлетворительно», ![]() «хорошо»,
«хорошо», ![]() «отлично», а термы
«отлично», а термы ![]() - промежуточные термы [1].
- промежуточные термы [1].
Взаимосвязь между входными и выходной переменной описывается нечеткими правилами вида
ЕСЛИ <значения входных переменных>, ТО <значение выходной переменной>.
Совокупность таких правил представляет собой нечеткую базу знаний.
Построение модели ![]() происходит в два этапа, которые можно (несколько условно) назвать этапами структурной и параметрической идентификации.
происходит в два этапа, которые можно (несколько условно) назвать этапами структурной и параметрической идентификации.
На первом этапе (этапе структурной идентификации) осуществляется формирование базы знаний и грубая настройка модели![]() , которая включает в себя выбор весов нечетких правил ЕСЛИ-ТО и форм функций принадлежности.
, которая включает в себя выбор весов нечетких правил ЕСЛИ-ТО и форм функций принадлежности.
Суть второго этапа (этапа параметрической идентификации) состоит в тонкой настройке модели ![]() , которая заключается в подборе таких весов нечетких правил ЕСЛИ-ТО и таких параметров функций принадлежности, которые минимизируют различие между экспериментальным и желаемым поведением объекта.
, которая заключается в подборе таких весов нечетких правил ЕСЛИ-ТО и таких параметров функций принадлежности, которые минимизируют различие между экспериментальным и желаемым поведением объекта.
Термы ![]() будем полагать нечеткими множествами, заданными на универсальном множестве
будем полагать нечеткими множествами, заданными на универсальном множестве ![]() :
:
 ,
, ![]() .
.
Здесь ![]() - функция принадлежности весового множителя
- функция принадлежности весового множителя ![]() терму
терму ![]() .
.
Аналогично, термы ![]() будем полагать нечеткими множествами, заданными на том же универсальном множестве
будем полагать нечеткими множествами, заданными на том же универсальном множестве ![]() :
:
 ,
, ![]() .
.
Здесь ![]() - функция принадлежности выходной переменной
- функция принадлежности выходной переменной ![]() терму
терму ![]() .
.
Положим, что выполнено N опытов по определению значений лингвистической переменной ![]() , их которых в
, их которых в ![]() опытах переменная
опытах переменная ![]() приняла значение
приняла значение ![]() , в
, в ![]() опытах - значение
опытах - значение ![]() и т.д. до
и т.д. до ![]() опытов, в которых переменная
опытов, в которых переменная ![]() приняла значение
приняла значение ![]() . Соответствующие входные векторы
. Соответствующие входные векторы ![]() обозначим
обозначим ![]() ,
, ![]() ,
, ![]() . Полученная матрица называется матрицей знаний и имеет вид, представленный в Табл. 1.
. Полученная матрица называется матрицей знаний и имеет вид, представленный в Табл. 1.
Таблица 1. Матрица знаний.
|
|
| … |
|
|
|
|
| … |
|
|
|
|
| … |
|
|
… | … | … | … | … | … |
|
|
| … |
|
|
|
|
| … |
|
|
|
|
| … |
|
|
… | … | … | … | … | … |
|
|
| … |
|
|
… | … | … | … | … | .. |
|
|
| … |
|
|
|
|
| … |
|
|
… | … | … | … | … | … |
|
|
| … |
|
|
Указанную матрицу знаний можно представить в виде системы логических высказываний
ЕСЛИ ![]() и
и ![]() и … и
и … и ![]() или
или
![]() и
и ![]() и … и
и … и ![]() или
или
……….
![]() и
и ![]() и … и
и … и ![]() ,
,
ТО ![]() .
.
С использованием операций объединения и пересечения множеств эта система может быть переписана в более компактном виде:
 ,
, ![]() .
.
Во введенных обозначениях схема нечеткого логического вывода Мамдани имеет следующий вид.
1). Для данного вектора ![]() определяем значение многомерной функции принадлежности
определяем значение многомерной функции принадлежности
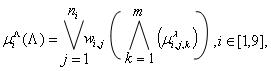
где ![]() - весовые множители,
- весовые множители, ![]() - символы логических операций ИЛИ, И, соответственно. Весовые множители
- символы логических операций ИЛИ, И, соответственно. Весовые множители ![]() будем определять с помощью модифицированного правила экспоненциального возрастания весов (см. п. 3) -
будем определять с помощью модифицированного правила экспоненциального возрастания весов (см. п. 3) - ![]() , где
, где ![]() - свободный параметр алгоритма, а величина
- свободный параметр алгоритма, а величина ![]() находится из условия
находится из условия ![]() . При вычислении значений функции
. При вычислении значений функции ![]() в качестве операции
в качестве операции ![]() используем одну из T-норм, а в качестве операции
используем одну из T-норм, а в качестве операции ![]() одну из S-норм.
одну из S-норм.
2). "Срезаем" функции принадлежности ![]() на уровне
на уровне ![]() ,
, ![]() .
.
3). Объединяем (агрегируем) полученные нечеткие множества – получаем нечеткое множество
![]()
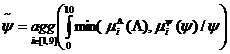
с функцией принадлежности ![]() . В качестве операции агрегирования обычно используется операция максимизации.
. В качестве операции агрегирования обычно используется операция максимизации.
4). Определяем четкое значение выхода ![]() , соответствующее входному вектору
, соответствующее входному вектору ![]() - т.е. выполняем операцию дефаззификации нечеткого множества
- т.е. выполняем операцию дефаззификации нечеткого множества ![]() , например, по методу центра тяжести.
, например, по методу центра тяжести.
Этап параметрической идентификации состоит в подборе таких параметров функций принадлежности ![]() и таких весовых множителей
и таких весовых множителей ![]() , которые минимизируют различие между экспериментальным и желаемым поведением объекта.
, которые минимизируют различие между экспериментальным и желаемым поведением объекта.
В нашем случае имеется всего три варьируемых параметра:
· Полуширина ![]() функций принадлежности
функций принадлежности ![]() ;
;
· полуширина ![]() функций принадлежности
функций принадлежности ![]() ;
;
· величина ![]() , определяющая закон изменения весовых множителей
, определяющая закон изменения весовых множителей ![]() .
.
Область допустимых значений варьируемых параметров ![]() определяется следующими ограничениями:
определяется следующими ограничениями: ![]() ;
; ![]() ;
; ![]() . Заметим, что ситуация
. Заметим, что ситуация ![]() означает, что вес нечеткого правила не изменяется с ростом соответствующего номера опыта.
означает, что вес нечеткого правила не изменяется с ростом соответствующего номера опыта.
Для параметрической идентификации построенной нечеткой модели необходима еще одна обучающая выборка ![]() ,
, ![]() ,
, ![]() В качестве критерия оптимальности при этом целесообразно принять критерий
В качестве критерия оптимальности при этом целесообразно принять критерий
 ,
, ![]()
![]() .
.
где ![]() - экспериментальное выходное значение нечеткой модели в точке
- экспериментальное выходное значение нечеткой модели в точке![]() – результат нечеткого логического вывода Мамдани в этой точке или, что тоже самое, значение аппроксимирующей по Мамдани функции в этой точке.
– результат нечеткого логического вывода Мамдани в этой точке или, что тоже самое, значение аппроксимирующей по Мамдани функции в этой точке.
Таким образом, формально задача параметрической идентификации формулируется следующим образом:
![]() . (11)
. (11)
Задача (11) является многомерной задачей условной оптимизации. Нет никаких оснований полагать, что эта задача является одноэкстремальной. Поэтому, вообще говоря, следует классифицировать ее как задачу глобальной оптимизации.
Обычно для решения задачи (11) используется метод наискорейшего спуска (с приближенным вычислением направления градиента с помощью конечных разностей). Для отыскания глобального экстремума приходится использовать поиск из разных начальных точек. При высокой размерности вектора ![]()
![]() и большом количестве нечетких правил в базе знаний часто используют методы случайного поиска, в частности, генетические методы оптимизации.
и большом количестве нечетких правил в базе знаний часто используют методы случайного поиска, в частности, генетические методы оптимизации.
7. Заключение
В работе рассмотрено использование персептронной нейронной сети, нейронной сети с радиальными базисными функциями, а также нечеткой логики для аппроксимации функции предпочтений ЛПР. На основе данных методов в последующих публикациях данной серии работ будут предложены адаптивные методы многокритериальной оптимизации.
Литература
1. Карпенко А.П., Федорук В.Г. Адаптивные методы решения задачи многокритериальной оптимизации. 1. Методы на основе планов первого порядка. //"Наука и образование: электронное научное издание. Инженерное образование", www.technomag.edu.ru, (╧ Гос. регистрации 0420700025, ЭЛ ╧ ФС 77-305 69), март, 2008,
╧0420800025/0007.
2. Карпенко А.П., Федорук В.Г. Адаптивные методы решения задачи многокритериальной оптимизации. 2. Методы на основе планов второго порядка. //"Наука и образование: электронное научное издание. Инженерное образование", www.technomag.edu.ru, (╧ Гос. регистрации 0420700025, ЭЛ ╧ ФС 77-305 69), март, 2008, ╧0420800025/0008.
3. Хайкин С. Нейронные сети. Полный курс. –М.: ООО «И.Д.Вильямс», 2008. -1104 с.
4. Загоруйко Н.Г. Прикладные методы анализа данных и знаний, Новосибирск, Изд-во Ин-та математики, 1999 г.-270 с.
5. Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере. -Новосибирск, Наука, 1996. -276 с.
6. Галушкин А. И. О методике решения задач в нейросетевом логическом базисе. - М.: Новые технологии, 2006. - 24 с. - (Приложение к журналу "Информационные технологии"; ╧ 9/2006).
7. Головко В. А. Нейронные сети: обучение, организация и применение. -М.: Радиотехника, 2001. -256 с.
8. Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации. –М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. -440 с.
9. LeCun Y., Bottou L., Orr G.B., Muller K.-R. Efficient BackProp //Neural Networks: Tricks of the Trade. Lecture Notes in Computer Science, Vol. 1524 - Springer, 1998, 432 p.
10. Poggio Т., Girosi F. Networks for approximation and learning //Proceedings of the IEEE, 1990, ╧ 9. – pp. 1481—1497.
11. Воронцов К.В. Лекции по искусственным нейронным сетям, www.ccas.ru/voron/download/NeuralNets.pdf
12. Круглов В. В., Борисов В.В. Искусственные нейронные сети. Теория и практика. - М.: Радио и связь, 2000. -382 с.
13. Ротштейн А.П. Интеллектуальные технологии идентификации //http://matlab.exponenta.ru/fuzzylogic/book5/references.php
14. Норвич А.М., Турксен И.Б. Фундаментальное измерение нечеткости. В сб.: Нечеткие множества и теория возможностей. - М: Радио и связь, 1986, с.54-64.
Публикации с ключевыми словами: нейронные сети
Публикации со словами: нейронные сети
Смотри также:
- Прогнозирование уровня глюкозы в крови больных инсулинозависимым диабетом нейронными сетями и методом экстраполяции по выборке максимального подобия
- 77-30569/409197 Использование комбинированной структуры искусственной нейронной сети для распознавания образов
- 77-30569/280351 Исследование быстродействия нейросетевого распознавателя почерка.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||