научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2013
DOI: 10.7463/0913.0603388
УДК 519.6
Россия, МГТУ им. Н.Э. Баумана
Введение
В последние годы интенсивно развивается новый класс стохастических поисковых методов оптимизации, которые называют по-разному: поведенческие, интеллектуальные, метаэвристические методы, методы вдохновленные (инспирированные) природой, роевые, многоагентные, популяционные методы. Используем последний термин как, на наш взгляд, наиболее точно передающий суть этих методов. Обзор большого числа популяционных методов (populationmethods), предназначенных для решения задачи глобальной непрерывной оптимизации, представлен в работе [1].
В настоящее время наиболее развитыми являются следующие популяционные методы оптимизации, вдохновленные живой природой ‑ методы роя частиц, муравьиной колонии, пчелиного роя. Достаточно широко известны также такие методы данного класса, как иммунный, бактериальный, светлячковый, сорняковый, обезьяний, прыгающих лягушек, летучих мышей, косяка рыб, растущих деревьев, мух, биогеографии [1, 2]. К этому же классу относится рассматриваемый в работе метод кукушки (CuckooSearch, CS).
Вообще говоря, популяционные методы широко используются для решения задач, как непрерывной, так и дискретной оптимизации. В данной работе рассматриваем задачу глобальной непрерывной оптимизации.
Метод кукушки предложен и разработан Янгом (Xin-SheYang) и Дебом (Suash Deb) в 2009 году [3]. На создание метода авторов вдохновило поведение кукушек в процессе вынужденного гнездового паразитизма, когда некоторые виды кукушек подкладывают яйца в гнезда птиц других видов.
Одной из основных особенностей популяционных методов глобальной оптимизации является наличие большого числа свободных параметров. С одной стороны, от значений этих параметров существенно зависит эффективность методов. С другой стороны, как правило, отсутствуют рекомендации по выбору значений, которые являются оптимальными для того или иного класса задач оптимизации. CS-метод выгодно отличается от большинства перечисленных выше популяционных методов малым числом свободных параметров (всего два).
Для повышения эффективности CS-метода предложено несколько модификаций канонического варианта этого метода [4, 5]. Кроме того, известны модификации CS-метода на основе его гибридизации с другими метаэвристическими методами. Например, в работе [6] предложена гибридизация CS-метода с методом роя частиц. Расширение CS-метода для решения задачи многокритериальной оптимизации рассмотрено в работе [7].
Целью данной работы является повышение эффективности канонического CS-метода. Для этого в работе предложены две модификации метода и выполнено исследование эффективности этих модификаций на ряде известных тестовых задач, включая практически значимую задачу о минимизации расходов на изготовление сосуда высокого давления.
В первом разделе работы даем постановку задачи глобальной непрерывной оптимизации. В этом же разделе приводим схемы канонического CS-метода и двух его наиболее известных модификаций. Во втором разделе представляем предлагаемые авторами модификации CS-метода. Третий раздел содержит описание программного обеспечения, реализующего канонический CS-метод и его авторские модификации. В четвертом разделе представлены результаты исследования эффективности разработанного методического, алгоритмического и программного обеспечения. В пятом разделе эффективность предложенных модификаций демонстрируем на примере тестовой практически значимой задачи о минимизации расходов на изготовление сосуда высокого давления.
1 Постановка задачи и схема канонического метода кукушки
В общей постановке рассматриваем детерминированную непрерывную задачу глобальной условной минимизации
 , (1)
, (1)
где ![]() – скалярная целевая функция (критерий оптимальности),
– скалярная целевая функция (критерий оптимальности), ![]() – искомое минимальное значение целевой функции,
– искомое минимальное значение целевой функции, ![]() –
– ![]() -мерный вектор варьируемых параметров,
-мерный вектор варьируемых параметров, ![]() – множество допустимых значений этого вектора,
– множество допустимых значений этого вектора, ![]() –
– ![]() -мерное арифметическое пространство.
-мерное арифметическое пространство.
CS-метод ориентирован на решение задачи безусловной оптимизации, когда ![]() . Каждое яйцо в гнезде представляет собой решение, а яйцо кукушки представляет новое решение. Цель заключается в использовании нового и потенциально лучшего решения (кукушкиного), чтобы заменить не очень хорошие решения в гнездах. В простейшей форме в каждом гнезде находится по одному яйцу. Метод может быть расширен на более сложный случай, когда в каждом из гнезд находится несколько яиц, представляющих некоторую совокупность потенциальных решений.
. Каждое яйцо в гнезде представляет собой решение, а яйцо кукушки представляет новое решение. Цель заключается в использовании нового и потенциально лучшего решения (кукушкиного), чтобы заменить не очень хорошие решения в гнездах. В простейшей форме в каждом гнезде находится по одному яйцу. Метод может быть расширен на более сложный случай, когда в каждом из гнезд находится несколько яиц, представляющих некоторую совокупность потенциальных решений.
CS-метод основан на трех следующих правилах.
1) Каждая кукушка откладывает одно яйцо за один раз и подкладывает его в гнездо, которое выбирается случайным образом.
2) Лучшие гнезда с яйцами высокого качества переходят в следующее поколение.
3) Число доступных гнезд фиксировано, и яйцо кукушки может быть обнаружено хозяином с вероятностью  . Обнаружение воздействует на некоторый набор худших гнезд, и обнаруженные решения исключаются из дальнейших вычислений, а взамен случайным образом создается соответствующее число новых решений.
. Обнаружение воздействует на некоторый набор худших гнезд, и обнаруженные решения исключаются из дальнейших вычислений, а взамен случайным образом создается соответствующее число новых решений.
Схема канонического CS-метода имеет следующий вид.
1) Инициализируем популяцию ![]() из
из ![]() хозяйских гнезд, то есть определяем начальные значения компонентов векторов
хозяйских гнезд, то есть определяем начальные значения компонентов векторов ![]() .
.
2) Выполняем случайные перемещения кукушки в пространстве поиска с помощью полетов Леви (Lévy Flights) [3] и находим ее новое положение ![]() .
.
3) Случайным образом выбираем гнездо ![]() , и если
, и если ![]() , то заменяем яйцо в этом гнезде на яйцо кукушки, то есть, полагаем
, то заменяем яйцо в этом гнезде на яйцо кукушки, то есть, полагаем ![]() .
.
4) С вероятностью ![]() удаляем из популяции некоторое число случайно выбранных гнезд и по правилам шага 1 строим такое же число новых гнезд.
удаляем из популяции некоторое число случайно выбранных гнезд и по правилам шага 1 строим такое же число новых гнезд.
5) Если условие окончания итераций не выполнено, то переходим к шагу 2.
При создании нового решения ![]() полеты Левиосуществляем по формуле
полеты Левиосуществляем по формуле
![]() . (2)
. (2)
Здесь ![]() –
– ![]() -мерный вектор независимых вещественных случайных чисел, распределенных по закону Леви
-мерный вектор независимых вещественных случайных чисел, распределенных по закону Леви
![]() ,
, ![]() ; (3)
; (3)
![]() – символ покомпонентного произведения векторов;
– символ покомпонентного произведения векторов; ![]() – вектор размера шагов;
– вектор размера шагов; ![]() . Обычно все компоненты последнего вектора полагают одинаковыми и равными
. Обычно все компоненты последнего вектора полагают одинаковыми и равными ![]() , где величина
, где величина ![]() должна быть связана с масштабами области поиска.
должна быть связана с масштабами области поиска.
Заметим, что большинство популяционных алгоритмов глобальной оптимизации используют миграционный оператор вида (2), но равномерное либо нормальное распределение величины шага. Полеты Леви представляют собой один из вариантов случайных блужданий, когда для определения случайной длины шага используется распределение Леви (3), имеющее длинный, медленно убывающий «хвост». Различные исследования показывают, что многие птицы и насекомые в процессе полета демонстрирует типичные характеристики полетов Леви. Поведение человека, например, охотника-собирателя, также показывает черты полетов Леви. Одним из самых эффективных алгоритмов численной генерации псевдослучайных чисел, распределенных по закону Леви, является алгоритм Мантенья (Mantegna) [8].
2 Модификации метода кукушки
В каноническом CS-методе при инициализации устанавливают фиксированные значения параметров ![]() и
и![]() , не изменяющиеся с ростом числа поколений. Однако, если значение
, не изменяющиеся с ростом числа поколений. Однако, если значение ![]() мало, а значение
мало, а значение ![]() велико, то может иметь место медленная сходимость метода. Напротив, если значение
велико, то может иметь место медленная сходимость метода. Напротив, если значение ![]() велико, а значение
велико, а значение ![]() мало, то скорость сходимости метода, как правило, высока, но низка вероятность локализации глобального минимума целевой функции (метод может «застрять» в локальном минимуме).
мало, то скорость сходимости метода, как правило, высока, но низка вероятность локализации глобального минимума целевой функции (метод может «застрять» в локальном минимуме).
Для преодоления указанных недостатков канонического CS-метода в работе [5] предложен улучшенный метод, суть которого состоит в корректировке значений свободных параметров ![]() и
и ![]() в процессе итераций по формулам
в процессе итераций по формулам
 , (4)
, (4)
![]() . (5)
. (5)
Здесь ![]() ‑ номер поколения,
‑ номер поколения, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – заданные константы,
– заданные константы, ![]() - максимально допустимое число поколений,
- максимально допустимое число поколений,
 .
.
Из формул (4), (5) следует, что в улучшенном CS-методе вероятность ![]() удаления из популяциихудших гнезд с ростом номера поколения линейно убывает от величины
удаления из популяциихудших гнезд с ростом номера поколения линейно убывает от величины ![]() до величины
до величины ![]() , а длина шага
, а длина шага ![]() экспоненциально убывает от
экспоненциально убывает от ![]() до
до ![]() .
.
Предложенные нами модификации CS-метода называем CS-A1, CS-P1, CS-A2, CS-P2.
МодификацияCS-A1 предполагает уменьшение длины шага по степенному закону
![]() , (6)
, (6)
где![]() – коэффициент затухания. Исходим из предположения, что данный закон позволит более тщательно исследовать окрестность найденного минимума и тем самым повысить точность его локализации.
– коэффициент затухания. Исходим из предположения, что данный закон позволит более тщательно исследовать окрестность найденного минимума и тем самым повысить точность его локализации.
МодификацияCS-P1. Суть этой модификации заключается в том, что по формуле, аналогичной формуле (6), с ростом номера поколения ![]() уменьшается вероятность обнаружения гнезд:
уменьшается вероятность обнаружения гнезд:
![]() ,
, ![]() . (7)
. (7)
Характер зависимостей (6), (7) иллюстрирует рисунок 1.
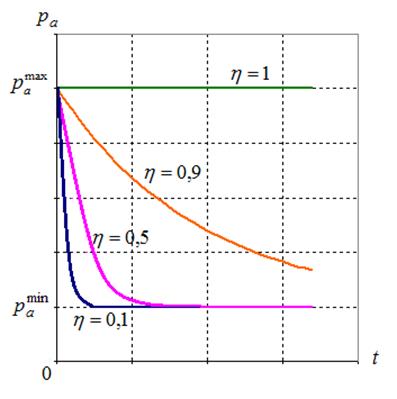
Рисунок 1 – К модификации CS-P1: вероятность обнаружения гнезд ![]() в функции номера поколения
в функции номера поколения ![]()
МодификацияCS-A2 заключается в коррекции длины шага ![]() на каждой итерации по следующей схеме:
на каждой итерации по следующей схеме:
‑ если после выполнения полетов кукушки не удалось улучшить достигнутое лучшее значение целевой функции, то полагаем, что шаг слишком велик и уменьшаем его по формуле
![]() ,
, ![]() ;
;
‑ в противном случае увеличиваем шаг по формуле
![]() ,
, ![]() .
.
МодификацияCS-P2. Данная модификация предполагает различную вероятность обнаружения «хороших» и «плохих» гнезд. Идея модификации заключается в следующем. Если решение в гнезде «хорошее», то вероятность разрушения этого гнезда должна быть низкой. Напротив, вероятность разрушения гнезд с «плохими» решениями следует повышать.
Для реализации указанной идеи на итерации ![]() сортируем все гнезда по возрастанию соответствующих значений целевой функции (убыванию качества решений) и присваиваем им номера от 1 до
сортируем все гнезда по возрастанию соответствующих значений целевой функции (убыванию качества решений) и присваиваем им номера от 1 до ![]() . Вероятности обнаружения гнезда с номером
. Вероятности обнаружения гнезда с номером ![]() присваиваем значение
присваиваем значение
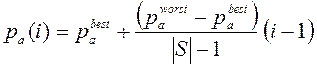 . (8)
. (8)
Здесь ![]() ,
, ![]() – свободные параметры модификации (рисунок 2).
– свободные параметры модификации (рисунок 2).

Рисунок 2 – К модификации CS-P2: вероятность обнаружения гнезда в функции его номера в отсортированном списке гнезд
Рассматриваем задачу условной оптимизации, когда множество допустимых значений вектора варьируемых параметров ![]() представляет собой параллелепипед
представляет собой параллелепипед
![]() ,
,
где ![]() ‑ его нижняя и верхняя границы по
‑ его нижняя и верхняя границы по ![]() -му измерению. Используем известный метод проецирования недопустимой точки на границу параллелепипеда (рисунок 3).
-му измерению. Используем известный метод проецирования недопустимой точки на границу параллелепипеда (рисунок 3).
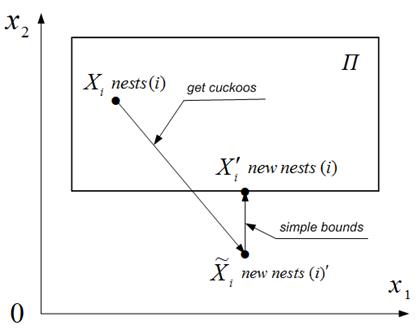
Рисунок 3 – К схеме учета ограничений: ![]()
CS-метод и его модификации, представленные выше, реализованы в среде MATLAB. Основными функциями программной реализации являются get cuckoos ( ) и simple bounds ( ).
Функция get cuckoos ( ) применяется ко всем элементам массива гнезд nests и возвращает новый массив new nests, содержащий новые решения, полученные в результате полетов Леви кукушки.
Если после полетов кукушки получаются недопустимые значения координат вектора ![]() (находящиеся вне параллелепипеда
(находящиеся вне параллелепипеда ![]() ), то возврат этих решений в параллелепипед осуществляется с помощью функции simple bounds ( ), схему работы которой иллюстрирует рисунок 3.
), то возврат этих решений в параллелепипед осуществляется с помощью функции simple bounds ( ), схему работы которой иллюстрирует рисунок 3.
4 Исследование эффективности
Рассматриваем задачу глобальной многомерной безусловной оптимизации. В качестве тестовых используем перечисленные ниже функции, для каждой из которых ![]() ;
; ![]() .
.
1) Квадратичная функция
 .
.
2) Функция Растригина
 .
.
3) Функция Экли
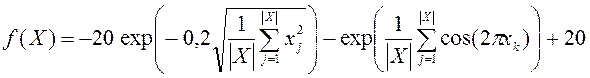 .
.
В качестве критериев эффективности метода и его модификаций используем следующие величины, полученные на основе ![]() запусков (стартов) соответствующей программы:
запусков (стартов) соответствующей программы:
‑ квантили 0,25, 0,5 и 0,75 числа испытаний ![]() (числа вычислений значений целевой функции);
(числа вычислений значений целевой функции);
- ![]() ‑ оценка вероятности локализации глобального экстремума.
‑ оценка вероятности локализации глобального экстремума.
Если не оговорено иное, исследование выполнено при следующих значениях свободных параметров метода и модификаций: ![]() ;
; ![]() . В качестве условия окончания итераций используем условие достижения минимального значения целевой функции с заданной точностью, равной
. В качестве условия окончания итераций используем условие достижения минимального значения целевой функции с заданной точностью, равной ![]() .
.
4.1 Канонический метод кукушки
Варьируемый параметр ‑ число гнезд ![]() . Результаты исследования иллюстрируют таблицы 1, 2 и рисунки 4 – 6.
. Результаты исследования иллюстрируют таблицы 1, 2 и рисунки 4 – 6.
Таблицы 1, 2 показывают, что для указанных функций число гнезд ![]() большее 16 обеспечивает оценку вероятности локализации глобального экстремума, равную 100%, как минимум, до размерности пространства поиска
большее 16 обеспечивает оценку вероятности локализации глобального экстремума, равную 100%, как минимум, до размерности пространства поиска ![]() , равной 8.
, равной 8.
Таблица 1 – Оценка вероятности ![]() локализации глобального минимума: канонический CS-метод; функция Растригина;
локализации глобального минимума: канонический CS-метод; функция Растригина; ![]() ;
; ![]()
|
|
|
|
4 | 87 | 42 | 2 |
8 | 99 | 98 | 45 |
16 | 100 | 100 | 98 |
32 | 100 | 100 | 100 |
64 | 100 | 100 | 100 |
128 | 100 | 100 | 100 |
Таблица 2 – Оценка вероятности ![]() локализации глобального минимума: канонический CS-метод; функция Экли;
локализации глобального минимума: канонический CS-метод; функция Экли; ![]() ;
; ![]()
|
|
|
|
4 | 97 | 91 | 3 |
8 | 100 | 100 | 95 |
16 | 100 | 100 | 100 |
32 | 100 | 100 | 100 |
64 | 100 | 100 | 100 |
128 | 100 | 100 | 100 |

а) ![]()

б) ![]()
Рисунок 4 – Зависимость числа испытаний ![]() от числа гнезд
от числа гнезд ![]() :
:
канонический CS-метод; квадратичная функция;![]() ;
; ![]()

а) ![]()

б) ![]()
Рисунок 5 – Зависимость числа испытаний ![]() от числа гнезд
от числа гнезд ![]() :
:
канонический CS-метод; функция Растригина;![]() ;
; ![]()

а) ![]()

б) ![]()
Рисунок 6 – Зависимость числа испытаний ![]() от числа гнезд
от числа гнезд ![]() :
:
канонический CS-метод; функция Экли;![]() ;
; ![]()
На рисунках 4 – 6 и далее белая линия соответствует медиане; черная область – интерквартильному размаху, в котором заключено 50% всех экспериментальных значений; серая область – аналогичной величине, включающей в себя 95% этих значений.
Представленные результаты показывают, что для канонического CS-метода зависимость числа испытаний от числа гнезд близка к линейной, и что оптимальное число гнезд следует определять, исходя из требуемой вероятности локализации глобального минимума целевой функции. С увеличением размерности пространства поиска примерно пропорционально возрастает требуемое число испытаний, а также число гнезд, необходимых для локализации минимума целевой функции с высокой вероятностью. При прочих равных условиях, требуемое число гнезд зависит от ландшафта целевой функции – увеличение числа локальных минимумов требует увеличения числа гнезд.
Варьируемый параметр ‑ вероятность обнаружения гнезд ![]() . Результаты данного исследования для величин шага
. Результаты данного исследования для величин шага ![]() , равных
, равных ![]() и
и ![]() , представлены на рисунках 7 - 10.
, представлены на рисунках 7 - 10.

а) ![]()

б) ![]()
Рисунок 7 – Число испытаний ![]() в функции вероятности
в функции вероятности ![]() :
:
канонический CS-метод; функция Растригина; ![]() ;
; ![]()
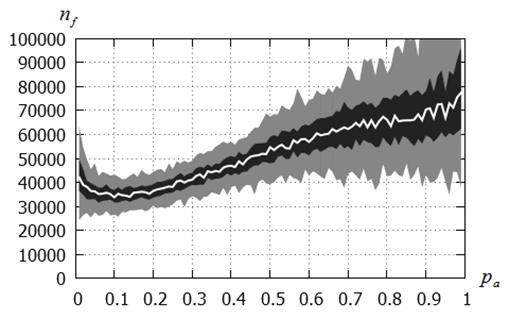
а) ![]()
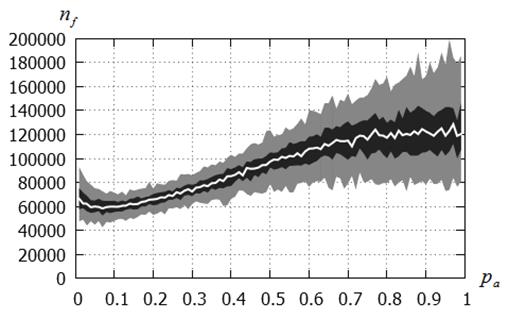
б) ![]()
Рисунок 8 – Число испытаний ![]() в функции вероятности
в функции вероятности ![]() :
:
канонический CS-метод; функция Растригина; ![]() ;
; ![]()
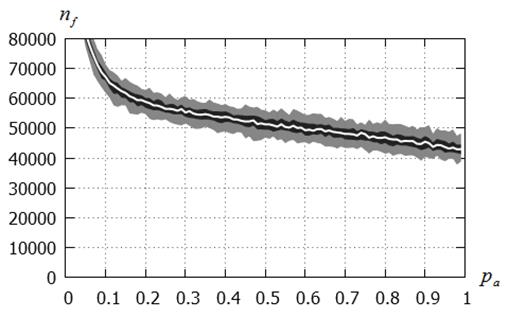
а) ![]()

б) ![]()
Рисунок 9 – Число испытаний ![]() в функции вероятности
в функции вероятности ![]() :
:
канонический CS-метод; функция Экли; ![]() ;
; ![]()

а) ![]()
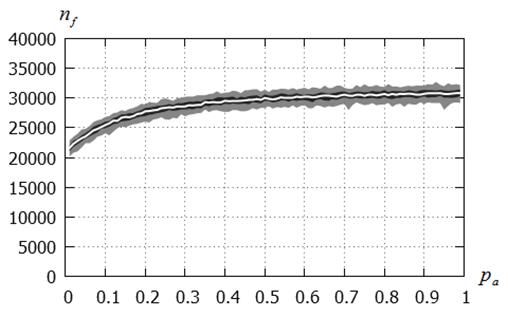
б) ![]()
Рисунок 10 – Число испытаний ![]() в функции вероятности
в функции вероятности ![]() :
:
канонический CS-метод; функция Экли; ![]() ;
; ![]()
Рисунки 7 – 10 показывают, что для каноническогоCS-метода имеет место различный характер зависимости числа испытаний от вероятностиобнаружения гнезда для функций Растригина и Экли. Для функции Растригина наблюдаем ярко выраженный минимум в зависимости ![]() , достигаемый при значениях
, достигаемый при значениях ![]() , принадлежащих интервалу [0,1; 0,3]. Использование значений этой величины близких к единице оказывается явно нецелесообразным вследствие значительного увеличения числа испытаний. Для функции Экли число испытаний слабо зависит от вероятности
, принадлежащих интервалу [0,1; 0,3]. Использование значений этой величины близких к единице оказывается явно нецелесообразным вследствие значительного увеличения числа испытаний. Для функции Экли число испытаний слабо зависит от вероятности ![]() : в интервале
: в интервале ![]() это число практически не меняется.
это число практически не меняется.
В целом, на основании данного исследования можно сделать вывод о целесообразности фиксации значения величины ![]() в интервале [0,1;0,3]. На этом основании исследование вероятности локализации глобального минимума (см. выше), а также представленное ниже исследование, выполнены при
в интервале [0,1;0,3]. На этом основании исследование вероятности локализации глобального минимума (см. выше), а также представленное ниже исследование, выполнены при ![]() .
.
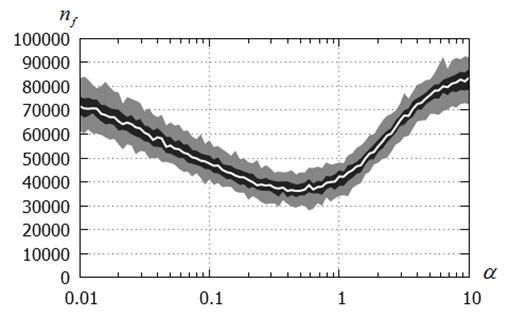
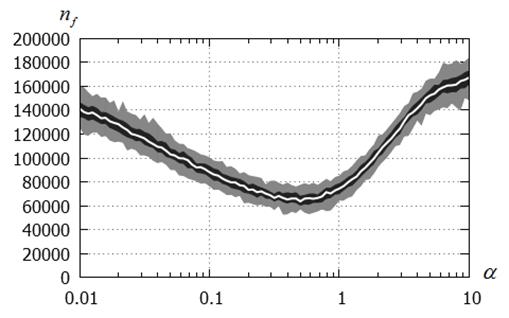
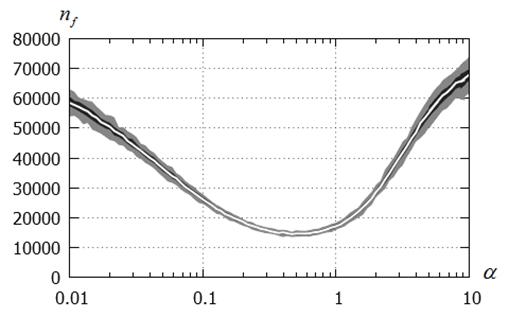
Варьируемый параметр - длина шага ![]() . Рисунки 7 - 10 показывают, что имеет место сильная зависимость числа испытаний
. Рисунки 7 - 10 показывают, что имеет место сильная зависимость числа испытаний ![]() от величины шага
от величины шага ![]() . Рисунки 11, 12 подтверждают данный факт и иллюстрируют эту зависимость.
. Рисунки 11, 12 подтверждают данный факт и иллюстрируют эту зависимость.
а) ![]()
б) ![]()
Рисунок 11 – Число испытаний ![]() в функции величины шага
в функции величины шага ![]() :
:
канонический CS-метод; функция Растригина; ![]() ;
; ![]()
а) ![]()

б) ![]()
Рисунок 12 – Число испытаний ![]() в функции величины шага
в функции величины шага ![]() :
:
канонический CS-метод; функция Экли; ![]() ;
; ![]()
Из рисунков 11, 12 следует, что при высокой вычислительной сложности целевой функции правильный выбор длины шага может позволить ускорить решение задачи в несколько раз. На основании этих же рисунков в качестве оптимального значения шага можно рекомендовать величину ![]() . Именно на этом основании исследование вероятности локализации глобального минимума целевой функции выполнено при этом значении шага (см. выше).
. Именно на этом основании исследование вероятности локализации глобального минимума целевой функции выполнено при этом значении шага (см. выше).
4.2 Модификации канонического метода
По схеме, аналогичной рассмотренной, выполнено исследование эффективности модификаций CS-P1 и CS-P2 (п. 2). Исследование подтвердило сделанный выше вывод о слабом влиянии значений параметра ![]() на требуемое число испытаний
на требуемое число испытаний ![]() . На этом основании мы не приводим результаты исследования эффективности указанных модификаций, а ограничиваемся рассмотрением только модификаций CS-A1 и CS-A2.
. На этом основании мы не приводим результаты исследования эффективности указанных модификаций, а ограничиваемся рассмотрением только модификаций CS-A1 и CS-A2.
Модификация CS-A1. Исследование выполнено при следующих значениях свободных параметров метода: ![]() ;
; ![]() 32;
32; ![]() =0,3;
=0,3; ![]() =0,001. Значения параметров
=0,001. Значения параметров ![]() варьировались в пределах
варьировались в пределах ![]() ,
, ![]() соответственно. Результаты исследования представлены на рисунках 13 – 15.
соответственно. Результаты исследования представлены на рисунках 13 – 15.

Рисунок 13 – Среднее число испытаний ![]() в функции параметров
в функции параметров ![]() и
и ![]() : модификация CS-A1; квадратичная функция;
: модификация CS-A1; квадратичная функция; ![]() ;
; ![]() 32;
32; ![]() =0,3;
=0,3; ![]() =0,001
=0,001

Рисунок 14 – Среднее число испытаний ![]() в функции параметров
в функции параметров ![]() и
и ![]() : модификация CS-A1; функция Растригина;
: модификация CS-A1; функция Растригина; ![]() ;
; ![]() 32;
32; ![]() =0,3;
=0,3; ![]() =0,001
=0,001

Рисунок 15 – Среднее число испытаний ![]() в функции параметров
в функции параметров ![]() и
и ![]() : модификация CS-A1; функция Экли;
: модификация CS-A1; функция Экли; ![]() ;
; ![]() 32;
32; ![]() =0,3;
=0,3; ![]() =0,001
=0,001
Рисунки 13 – 15 показывают ожидаемую сильную зависимость числа испытаний от значения коэффициента затухания ![]() . При малых значениях этого коэффициента с ростом числа итераций шаг
. При малых значениях этого коэффициента с ростом числа итераций шаг ![]() быстрее достигнет своего минимального значения
быстрее достигнет своего минимального значения ![]() . В результате скорость сходимости модифицированного метода уменьшается, и растет требуемое число испытаний. При
. В результате скорость сходимости модифицированного метода уменьшается, и растет требуемое число испытаний. При ![]() модификация вырождается в канонический метод кукушки с постоянным значением шага, равным
модификация вырождается в канонический метод кукушки с постоянным значением шага, равным ![]() .
.
Модификация CS-A2. Исследование эффективности данной модификации выполнено при ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Рассмотрены диапазоны изменения значений свободных параметров
. Рассмотрены диапазоны изменения значений свободных параметров ![]() ,
, ![]() , равные соответственно
, равные соответственно ![]() ;
; ![]() . Основные результаты исследования представлены на рисунках 16 – 19.
. Основные результаты исследования представлены на рисунках 16 – 19.

а) ландшафт

б) линии уровня
Рисунок 16 – Среднее число испытаний ![]() в функции параметров
в функции параметров ![]() ,
, ![]() : модификация CS-A2; квадратичная функция;
: модификация CS-A2; квадратичная функция; ![]() ;
; ![]() ;
; ![]() ;
; ![]()

Рисунок 17 – Среднее число испытаний ![]() в функции параметров
в функции параметров ![]() ,
, ![]() . Линии уровня: модификация CS-A2; квадратичная функция;
. Линии уровня: модификация CS-A2; квадратичная функция; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
а) ландшафт
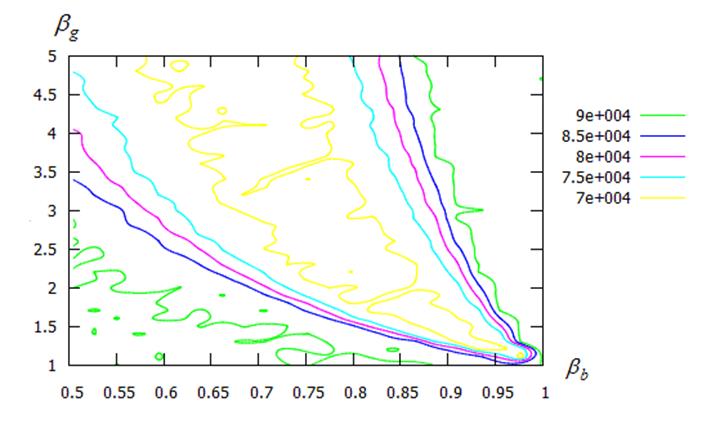
б) линии уровня
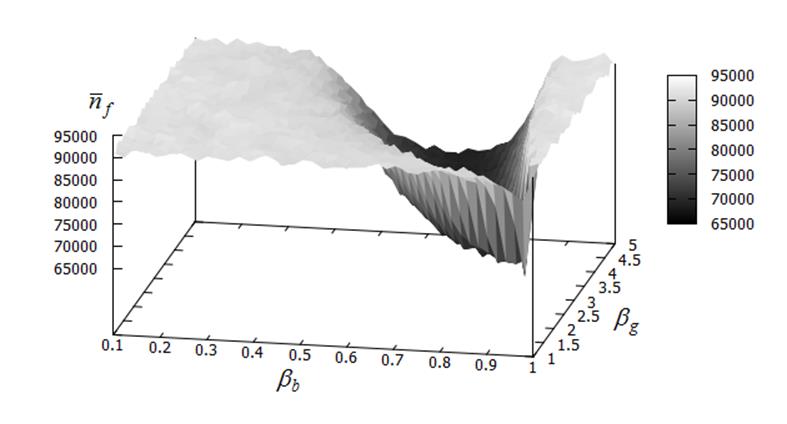
Рисунок 18 – Среднее число испытаний ![]() в функции значений параметров
в функции значений параметров ![]() ,
, ![]() : модификация CS-A2; функция Растригина;
: модификация CS-A2; функция Растригина; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
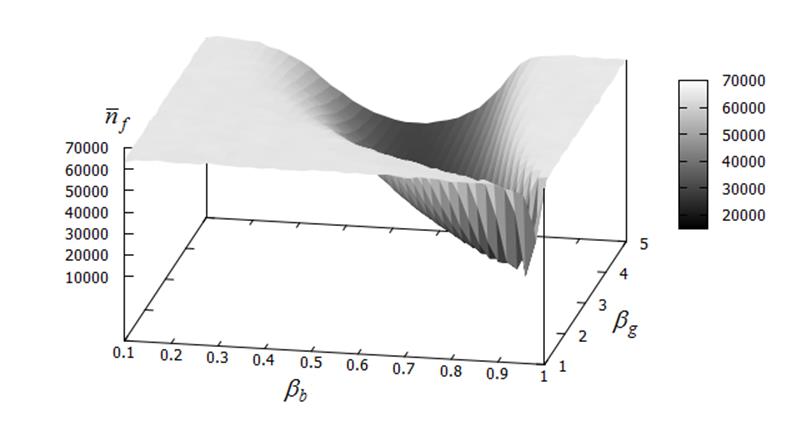
а) ландшафт
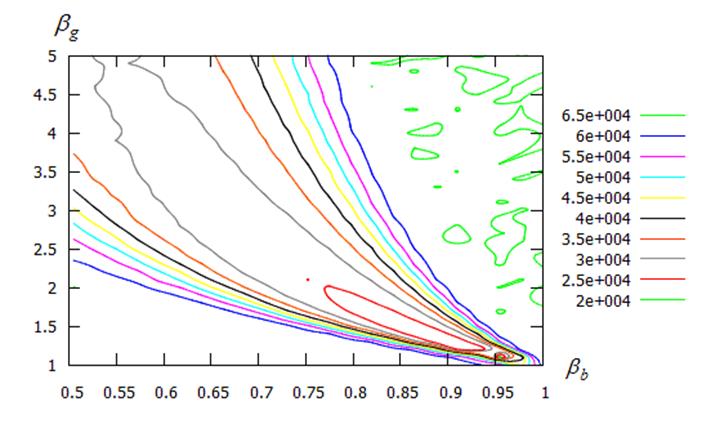
б) линии уровня
Рисунок 19 – Среднее число испытаний ![]() в функции значений параметров
в функции значений параметров ![]() ,
, ![]() : модификация CS-A2; функция Экли;
: модификация CS-A2; функция Экли; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Рисунки 16 – 19 показывают, что среднее число испытаний ![]() принимает минимальное значение, если значения свободных параметров
принимает минимальное значение, если значения свободных параметров ![]() ,
, ![]() лежат в интервалах
лежат в интервалах ![]() ,
, ![]() соответственно. На этом основании для дальнейших исследований принимаем
соответственно. На этом основании для дальнейших исследований принимаем ![]() ,
, ![]() . Широкий диапазон возможных значений свободных параметров
. Широкий диапазон возможных значений свободных параметров ![]() ,
, ![]() следует отнести к недостаткам модификации CS-A2.
следует отнести к недостаткам модификации CS-A2.
Зависимость числа испытаний ![]() от величины шага
от величины шага ![]() для указанных выше значений параметров
для указанных выше значений параметров ![]() ,
, ![]() представлена на рисунке 20. Рисунок показывает, что в диапазоне
представлена на рисунке 20. Рисунок показывает, что в диапазоне ![]() в модификации CS-A2 среднее число испытаний слабо зависит от величины шага
в модификации CS-A2 среднее число испытаний слабо зависит от величины шага ![]() . Это обстоятельство является значительным преимуществом данной модификации по сравнению с каноническим CS-методом, в котором длина шага оказывает сильное влияние на величину
. Это обстоятельство является значительным преимуществом данной модификации по сравнению с каноническим CS-методом, в котором длина шага оказывает сильное влияние на величину ![]() (рисунок 21). Это же обстоятельство позволяет в модификации CS-A2 использовать фиксированное значение величины шага.
(рисунок 21). Это же обстоятельство позволяет в модификации CS-A2 использовать фиксированное значение величины шага.

Рисунок 20 – Среднее число испытаний ![]() в функции величины шага
в функции величины шага ![]() : модификация CS-A2; квадратичная функция;
: модификация CS-A2; квадратичная функция; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
, ![]()

Рисунок 21 – Сравнение канонического CS-метода и его модификации CS-A2: квадратичная функция; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
, ![]()
5 Оптимизация затрат на изготовление сосуда высокого давления
Рассматриваем задачу изготовления сосуда высокого давления [9], показанного на рисунке 22. Целью является минимизация стоимости расхода материала на изготовление частей и последующей сварки сосуда.
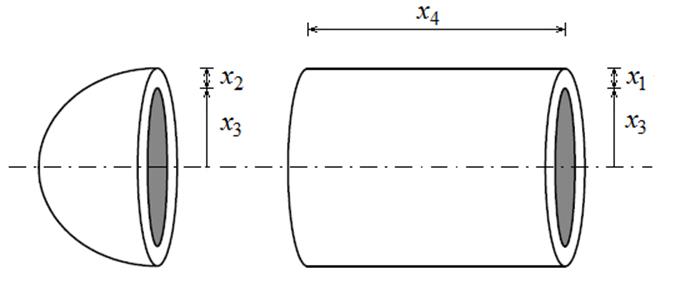
Рисунок 22 – Схема сосуда высокого давления
Вектор варьируемых параметров задачи ![]() состоит из четырех компонентов (все величины, полагаем, измеряются в дюймах):
состоит из четырех компонентов (все величины, полагаем, измеряются в дюймах):
· ![]() – толщина стенки цилиндра;
– толщина стенки цилиндра;
· ![]() – толщина сферической головки;
– толщина сферической головки;
· ![]() – внутренний радиус цилиндрической оболочки;
– внутренний радиус цилиндрической оболочки;
· ![]() – длина цилиндрической части.
– длина цилиндрической части.
Имеют место следующие ограничения (в дюймах) на указанные величины:
а) значения величин ![]() и
и ![]() должны быть кратны 0,0625 в соответствии с имеющейся толщиной листового проката стали, то есть должно быть справедливо выражение
должны быть кратны 0,0625 в соответствии с имеющейся толщиной листового проката стали, то есть должно быть справедливо выражение
 ,
, ![]() , (9)
, (9)
где ![]() - множество натуральных чисел;
- множество натуральных чисел;
б) внутренний радиус ![]() должен удовлетворять ограничению
должен удовлетворять ограничению
![]() ; (10)
; (10)
в) длина ![]() ‑ ограничению
‑ ограничению
![]() . (11)
. (11)
Кроме того, имеют место ограничения
![]() , (12)
, (12)
![]() , (13)
, (13)
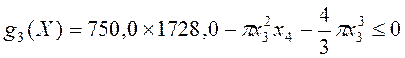 , (14)
, (14)
![]() , (15)
, (15)
![]() , (16)
, (16)
![]() (17)
(17)
Целевую функцию определяет выражение
![]() . (18)
. (18)
Ограничения (12) – (17) учитываем с помощью метода штрафных функций, используя функцию штрафа вида
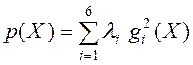 ,
,
где ![]() – весовые коэффициенты, изменяющиеся в процессе итераций так, чтобы обеспечить выполнение указанных ограничений. Таким образом, рассматриваем задачу
– весовые коэффициенты, изменяющиеся в процессе итераций так, чтобы обеспечить выполнение указанных ограничений. Таким образом, рассматриваем задачу
![]() ,
,
где параллелепипед ![]() формируют ограничения (10), (11). Для обеспечения выполнения ограничения (9) используем в качестве решений ближайшие к
формируют ограничения (10), (11). Для обеспечения выполнения ограничения (9) используем в качестве решений ближайшие к ![]() ,
, ![]() значения, кратные величине 0,0625.
значения, кратные величине 0,0625.
Результаты решения задачи (9) – (17), полученные с помощью модификации CS-A2 метода кукушки, представлены в таблице 3, в которой приведены также результаты решения этой задачи, полученные другими авторами.
Таблица 3 – Результаты решения задачи
| Метод ветвей и границ [10] | Генетический алгоритм [11] | Гармонический поиск [12] | Метод кукушки |
| 1,125 | 1,125 | 1,125 | 1,114 |
| 0,625 | 0,625 | 0,625 | 0,600 |
| 48,97 | 58,20 | 58,28 | 57,71 |
| 106,72 | 44,29 | 43,75 | 46,95 |
| -0,1790 | -0,0018 | -0,0002 | -0,0001 |
| -0,158 | -0,070 | -0,069 | -0,049 |
| 97,76 | -974,30 | -3,72 | -334,11 |
| -133,28 | -195,71 | -196,24 | -193,04 |
| 7980,89 | 7207,49 | 7198,43 | 7036,48 |
Сандгрен (Sandgren) в работе [10] использовал для решения рассматриваемой задачи метод ветвей и границ и получил оптимальное значение целевой функции, равное 7980,89. Однако, при этом условие ![]() оказалось не выполненным. Ву (Wu) и Чоу (Chow) применили для решения задачи метод, основанный на генетическом алгоритме [11]. Полученное ими лучшее значение целевой функции равно 7207,49. Ли (Lee) и Гим (Geem) в своей работе [12] использовали для решения данной задачи гармонический поиск и уменьшили значение целевой функции до 7198,43. Использованная нами модификация CS-A2 метода кукушки показала лучший результат по сравнению со всеми перечисленными работами – метод позволил достичь значения целевой функции, равного
оказалось не выполненным. Ву (Wu) и Чоу (Chow) применили для решения задачи метод, основанный на генетическом алгоритме [11]. Полученное ими лучшее значение целевой функции равно 7207,49. Ли (Lee) и Гим (Geem) в своей работе [12] использовали для решения данной задачи гармонический поиск и уменьшили значение целевой функции до 7198,43. Использованная нами модификация CS-A2 метода кукушки показала лучший результат по сравнению со всеми перечисленными работами – метод позволил достичь значения целевой функции, равного ![]() , и обеспечить выполнение всех ограничений (9) – (17).
, и обеспечить выполнение всех ограничений (9) – (17).
Заключение
В работе предложено несколько модификаций канонического метода кукушки, рассмотрена программная реализация этого метода и его указанных модификаций, представлены результаты широкого исследования эффективности предложенных модификаций на ряде тестовых функций, которое показало их преимущества по сравнению с каноническим методом. В последнем разделе работы рассмотрено решение с помощью одной из предложенных модификаций известной практической задачи о минимизации расходов на изготовление сосуда высокого давления. Показано, что предложенные модификации обеспечивают лучшее значение целевой функции по сравнению результатами, полученными другими авторами, и обеспечить выполнение всех ограничений.
В развитие работы авторы планируют разработку и исследование эффективности параллельных вариантов рассмотренных методов, ориентированных на различные классы параллельных вычислительных систем.
Список литературы
1. Карпенко А.П. Популяционные алгоритмы глобальной поисковой оптимизации. Обзор новых и малоизвестных алгоритмов // Приложение к журналу «Информационные технологии». 2012. № 7. C. 1-32.
2. Simon D. Biogeography-Based Optimization // IEEE Transactions on Evolutionary Computation. 2008. Vol. 12, no. 6. P. 702-713. DOI: 10.1109/TEVC.2008.919004
3. Yang X.-S., Deb S. Cuckoo search via L´evy flights // Proceedings of World Congress on Nature & Biologically Inspired Computing (NaBIC 2009). IEEE Publications, USA, 2009. P. 210-214.
4. Tuba M., Subotic M., Stanarevic N. Modified cuckoo search algorithm for unconstrained optimization problems // Proceedings of the 5th European Computing Conference (ECC 2011). 2011. P. 263-268.
5. Valian E., Mohanna S., Tavakoli S. Improved cuckoo search algorithm for feed forward neural network training // International Journal of Artificial Intelligence & Applications (IJAIA). 2011. Vol. 2, no. 3. P. 36-43.
6. Wang F., Lou L., He X., Wang Y. Hybrid optimization algorithm of PSO and Cuckoo Search // Proceedings of 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC 2011), 2011. P. 1172-1175.
7. Yang X.-S., Deb S. Multiobjective cuckoo search for design optimization // Computers and Operations Research. 2013. Vol. 40, no. 6. P. 1616-1624.
8. Mantegna R.N. Fast, accurate algorithm for numerical simulation of Levy stable stochastic processes // Physical Review E. 1994. Vol. 49, no. 5. P. 4677-4683.
9. Cagnina L.C., Esquivel S.C., Coello C.A.C. Solving Engineering Optimization Problems with the Simple Constrained Particle Swarm Optimizer // Informatica. 2008. Vol. 32, no. 3. P. 319-326.
10. Sandgren E. Nonlinear integer and discrete programming in mechanical design optimization // ASME Journal of Mechanical Design. 1990. Vol. 112, no. 2. P. 223-229.
11. Wu S.J., Chow P.T. Genetic algorithms for nonlinear mixed discrete-integer optimization problems via meta-genetic parameter optimization // Engineering Optimization. 1995. Vol. 24, no. 2. P. 137-159.
12. Lee K.S., Geem Z.W. New meta-heuristic algorithm for continuous engineering optimization: harmony search theory and practice // Computer Methods in Applied Mechanics and Engineering. 2005. Vol. 194, no. 36-38. P. 3902-3933.
Публикации с ключевыми словами: задача глобальной оптимизации, метод кукушки, популяционный метод
Публикации со словами: задача глобальной оптимизации, метод кукушки, популяционный метод
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



