научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2013
DOI: 10.7463/0913.0598978
УДК 531/534, 531.7, 53.043, 53.08, 53.091, 672.6
Россия, МГТУ им. Н.Э. Баумана
1. ПОСТАНОВКА ЗАДАЧИ
Модели динамики технологических систем обработки резанием включают в себя законы резания, являющиеся результатом обработки экспериментальных данных (например, [1-3]). Обычно законы для сил резания представляют в экспоненциальной форме вида [6, p. 555], например, для осевой силы при сверлении
![]() , (1)
, (1)
где ![]() измеряется в [Н],
измеряется в [Н], ![]() - экспериментальные постоянные с неопределённой размерностью,
- экспериментальные постоянные с неопределённой размерностью, ![]() - подача в [мм / об],
- подача в [мм / об], ![]() длина режущей кромки, обычно принимаемой равной удвоенному радиусу сверла, [мм],
длина режущей кромки, обычно принимаемой равной удвоенному радиусу сверла, [мм], ![]() твёрдость обрабатываемого материала по Бринелю, в [кг / мм2]. Очевидно, что зависимости вида являются аппроксимацией экспериментальных данных и могут использоваться только в указанной системе единиц. Никакого физического смысла такие зависимости не имеют. Основной вопрос, возникающий при анализе динамики технологических систем, состоит в следующем: каким образом следует изменить зависимости для использования их в уравнениях динамики, являющихся инвариантными по отношению к выбору системы единиц измерения?
твёрдость обрабатываемого материала по Бринелю, в [кг / мм2]. Очевидно, что зависимости вида являются аппроксимацией экспериментальных данных и могут использоваться только в указанной системе единиц. Никакого физического смысла такие зависимости не имеют. Основной вопрос, возникающий при анализе динамики технологических систем, состоит в следующем: каким образом следует изменить зависимости для использования их в уравнениях динамики, являющихся инвариантными по отношению к выбору системы единиц измерения?
Теорема об однородности [7] позволяет положительно ответить на этот вопрос: всякое соотношение между наблюдаемыми величинами ![]() – размерными переменными и постоянными – выражается однородной функцией, связывающей их величины
– размерными переменными и постоянными – выражается однородной функцией, связывающей их величины
![]() , (2)
, (2)
то есть
![]() , (3)
, (3)
где ![]() , коэффициенты перехода от одной системы единиц измерения к другой
, коэффициенты перехода от одной системы единиц измерения к другой ![]() , удовлетворяющих соотношениям
, удовлетворяющих соотношениям
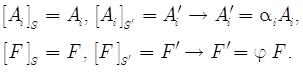 (4)
(4)
Экспериментально определяемые величины имеют разброс, связанный с шумом измерений, то есть, постоянные ![]() в не позволяют получить соотношения, удовлетворяющие преобразованию однородности по размерностям . Поэтому экспериментально получаемые зависимости следует получать с помощью методов теории подобия и анализа размерностей [7] – такой подход позволяет всегда получать однородные по размерностям физические соотношения между переменными, входящими в безразмерные комплексы. Появление безразмерных комплексов в качестве аргументов устанавливает дополнительные связи между физическими величинами без проведения дополнительных экспериментов.
в не позволяют получить соотношения, удовлетворяющие преобразованию однородности по размерностям . Поэтому экспериментально получаемые зависимости следует получать с помощью методов теории подобия и анализа размерностей [7] – такой подход позволяет всегда получать однородные по размерностям физические соотношения между переменными, входящими в безразмерные комплексы. Появление безразмерных комплексов в качестве аргументов устанавливает дополнительные связи между физическими величинами без проведения дополнительных экспериментов.
Анализ размерностей производится следующим образом. Определяется база единиц измерения ![]() . Размерность любого физического параметра
. Размерность любого физического параметра ![]() вычисляется как
вычисляется как
 (5)
(5)
Тогда вектор размерности параметра ![]() равен
равен
![]() (6)
(6)
В синтаксисе среды MATLABразмерность может быть представлена в виде
![]() (7)
(7)
Размерность некоторой физической величины ![]() будет иметь вид
будет иметь вид
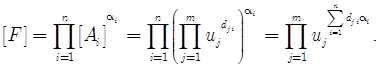 (8)
(8)
Соответствующий вектор размерности ![]() вычисляется как
вычисляется как
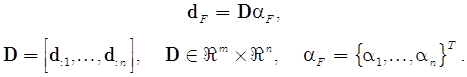 (9)
(9)
Если величина ![]() является безразмерным комплексом
является безразмерным комплексом ![]() , то
, то ![]() является нулевым вектором
является нулевым вектором
![]() (10)
(10)
Одна из целей настоящей работы состоит в разработке методики экспериментального определения сил резания, действующих на инструмент при сверлении, в безразмерной форме, позволяющей сравнивать результаты, получаемые разными исследователями и использовать получаемые зависимости в физических моделях, включающих в себя силы резания, в инвариантной форме.
2. МОДЕЛИРОВАНИЕ ПРОЦЕЕСА СВЕРЛЕНИЯ
Феноменологический подход к моделированию состоит, прежде всего, в перечислении всех существенных физических параметров, характеризующих явление. В случае сверления можно выделить четырнадцать параметров, приведённых в Таблице 1. Три из них являются безразмерными и служат критериями подобия, то есть ![]() :
:
![]() . (11)
. (11)
В качестве основных, независимых единиц измерений выберем ![]() ; количество базовых единиц равно
; количество базовых единиц равно ![]() . Определим вектор базовых единиц измерения
. Определим вектор базовых единиц измерения ![]() :
:
![]() . (12)
. (12)
Таким образом, можно определить семь критериев подобия – обобщённых переменных, характеризующих явление сверления: (14), (3), (4), (7). Общее выражение критерия подобия имеет вид степенного одночлена [6]
 (13)
(13)
Векторы размерностей одиннадцати определяющих параметров равны
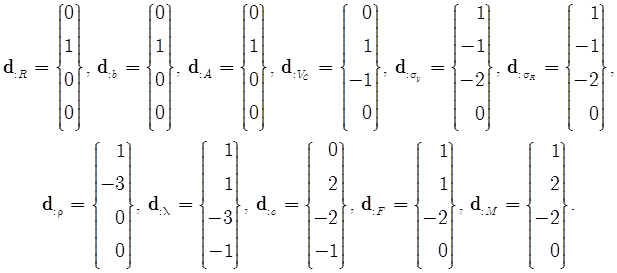 (14)
(14)
Для того, чтобы выражение было безразмерным, необходимо и достаточно равенство нулю показателей всех базовых единиц измерения . То есть, получаем следующие четыре линейных уравнения:
 (15)
(15)
В данном случае матрица ![]() имеет вид
имеет вид
 . (16)
. (16)
Строки матрицы ![]() соответствуют колонкам таблицы 1. Система содержит четыре уравнения с одиннадцатью неизвестными
соответствуют колонкам таблицы 1. Система содержит четыре уравнения с одиннадцатью неизвестными ![]() .
.
Это позволяет выбрать семь переменных вектора ![]() в качестве независимых -
в качестве независимых - ![]() (вектор 7´1) и, в качестве зависимых
(вектор 7´1) и, в качестве зависимых ![]() (вектор 4´1), и переписать в виде
(вектор 4´1), и переписать в виде
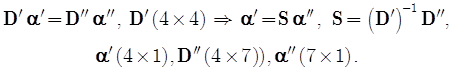 (17)
(17)
При этом имеется определённый произвол в выборе независимых переменных ![]() : необходимо проверить, чтобы выполнялось условие невырожденности системы уравнений –
: необходимо проверить, чтобы выполнялось условие невырожденности системы уравнений – ![]() . Например, это условие выполняется, если осуществить выбор в виде:
. Например, это условие выполняется, если осуществить выбор в виде:
![]() (18)
(18)
Таблица 1. Основные константы и переменные для сверления
| Имя переменной | Обозначение | Размерность | Показатели степени базовых единиц измерения | |||
|
|
|
| kg | m | s | K |
1 | Радиус сверла | R | m | 0 | 1 | 0 | 0 |
2 | Толщина перемычки | b | m | 0 | 1 | 0 | 0 |
3 | Угол заточки при вершине | G | 1 | 0 | 0 | 0 | 0 |
4 | Число режущих кромок | N | 1 | 0 | 0 | 0 | 0 |
5 | Подача на оборот | A | m | 0 | 1 | 0 | 0 |
6 | Скорость резания | VC | m / s | 0 | 1 | -1 | 0 |
7 | Предел текучести обрабатываемого материала | sy | N / m2 | 1 | -1 | -2 | 0 |
8 | Предел прочности обрабатываемого материала | sR | N / m2 | 1 | -1 | -2 | 0 |
9 | Относительное удлинение при разрушении обрабатываемого материала | d | 1 | 0 | 0 | 0 | 0 |
10 | Плотность обрабатываемого материала | r | kg / m3 | 1 | -3 | 0 | 0 |
11 | Теплопроводность обрабатываемого материала | l | W / m /K | 1 | 1 | -3 | -1 |
12 | Теплоёмкость обрабатываемого материала | c | J / kg / K | 0 | 2 | -2 | -1 |
13 | Осевая сила резания | F | N | 1 | 1 | -2 | 0 |
14 | Крутящий момент сил резания | M | N.m | 1 | 2 | -2 | 0 |
Список рассматриваемых существенных физических параметров не является исчерпывающим. При определённых условиях необходимо учитывать (характеризовать) явления адгезии между инструментом и обрабатываемым материалом, физические параметры прочности инструмента, и др.
Тогда, соответствующие матрицы равны ![]()
 (19)
(19)
Очевидно, что любая функциональная связь безразмерных параметров порождает безразмерную величину. Это позволяет выбрать в качестве базы безразмерные комплексы, получаемые от единичных векторов ei в арифметическом пространстве ℛ7: ![]() :
:
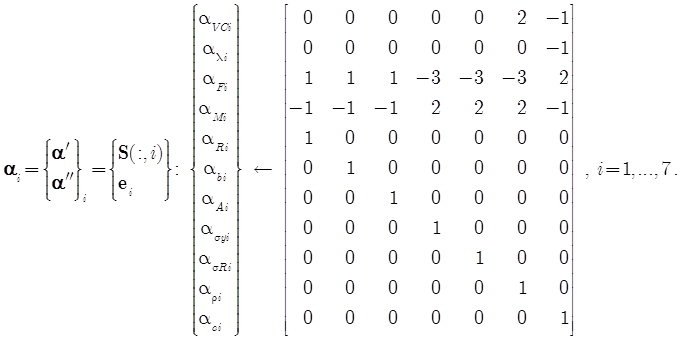 (20)
(20)
Каждая колонка матрицы (14) даёт вектор ai, образующий степени размерных параметров, образующих безразмерные комплексы, называемые критериями подобия :
 (21)
(21)
Таким образом, получаем семь критериев подобия:
 (22)
(22)
В приложении 1 представлен алгоритм определения всех возможных безразмерных комбинаций в синтаксе MATLAB. Всего генерируется 109 комбинаций по 7 безразмерных комплексов.
Из полученных комбинаций и формируются критерии подобия, удобные для обработки экспериментальных данных:
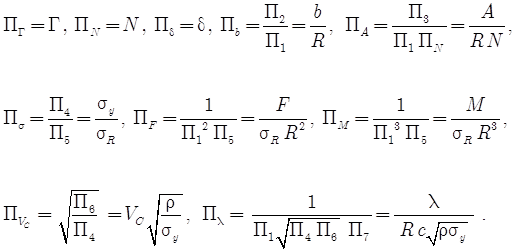 (23)
(23)
В частности, из безразмерных комплексов можно сформировать критерий подобия Пекле Pe, играющего фундаментальную роль при исследовании термических задач:
 (24)
(24)
Важно иметь в виду, что числа ![]() характеризуют геометрические и физические свойства системы инструмент - обрабатываемый материал; числа
характеризуют геометрические и физические свойства системы инструмент - обрабатываемый материал; числа ![]() – условия резания; числа
– условия резания; числа ![]() определяют измеряемые переменные во время обработки резанием.
определяют измеряемые переменные во время обработки резанием.
3. РАЗЛИЧНЫЕ ФОРМЫ ЗАКОНА РЕЗАНИЯ ПРИ СВЕРЛЕНИИ
Искомые зависимости могут быть представлены в следующей общей неявной форме
 (25)
(25)
Очевидно, что зависимости не зависят от системы единиц измерения.
Важно выбрать вид критериев подобия таким образом, чтобы управляемые и определяемые величины были сформированы независимым образом. Измеряемыми величинами в данном контексте являются функции ![]() . Форма позволяет автоматически удовлетворить однородности по размерностям в физических соотношениях. Выражения для силы и момента имеют вид
. Форма позволяет автоматически удовлетворить однородности по размерностям в физических соотношениях. Выражения для силы и момента имеют вид
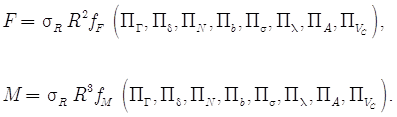 (26)
(26)
Для сверл с симметричным расположением режущих кромок возможно выразить в явном виде влияние числа PN = N:
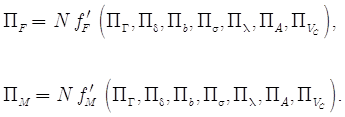 (27)
(27)
Зная, что для более пластичных материалов необходимо увеличить скорость резания, для получения подобных условий резания [8], возможно предположить, что числа ![]() образуют единый комплекс вида
образуют единый комплекс вида![]() :
:
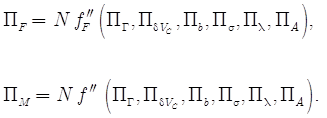 (28)
(28)
В определённом диапазоне изменения скоростей резания их влияние на усилия резания пренебрежимо мало [6, 8] Конечно, эта гипотеза должна быть пересмотрена, если влияние скорости существенно. Важно отметить, что если мы ограничиваемся критериями G, N, A, R, σR, VC, F, M, что является довольно распространённым случаем, - с точки зрения теории подобия и анализа размерностей, скорость резания не может образовать безразмерного комплекса, и, как следствие, усилия резания не могут зависеть от скорости резания. Это является строгим результатом и влияет на разработку плана эксперимента. Если наблюдается влияние скорости резания, то список параметров должен быть расширен!
Таким образом, можно упростить зависимости (22), опуская комплекс, содержащий ![]() :
:
 (29)
(29)
В большинстве исследований [6, 8] законы резания для F и M представляют в степенной или полиномиальной форме от подачи и радиуса сверла и пренебрегают термодинамическими эффектами. Учитывая, что подача и радиус входят в этом случае только в комплекс ![]() (17), функции
(17), функции ![]() могут быть записаны в следующей явной форме:
могут быть записаны в следующей явной форме:
 (30)
(30)
или:
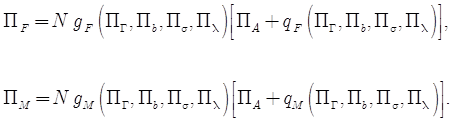 (31)
(31)
На практике формы или должны быть выбраны после изучения экспериментальных данных как наиболее подходящие для аппроксимации и природе явления. В определённых исследованиях полагают, что показатели qF, qM равны друг другу. Такое утверждение эквивалентно предположению, что осевые и окружные распределения сил вдоль режущих кромок подобны, что является достаточно сильным утверждением.
В случае получения законов резания для одного материала и для фиксированного типа инструмента критерии подобия ![]() не изменяются и функции
не изменяются и функции ![]() играют роль универсальных постоянных. Будем называть формы , законами с двумя постоянными
играют роль универсальных постоянных. Будем называть формы , законами с двумя постоянными ![]() :
:
![]() . (32)
. (32)
Аналогично , возможна трехконстантная (дробно – рациональная форма, которая в ряде случаев может быть адекватнее наблюдаемым данным [4]:
 (33)
(33)
В этом случае будем иметь формулы, аналогичные
![]() . (34)
. (34)
4. ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ {g, q} ДЛЯ ДВУХКОНСТАНТНЫХ ЗАКОНОВ
Чтобы продемонстрировать методику получения законов резания или было проведено три серии испытаний для трёх типов спиральных сверл с двумя режущими кромками (N = 2): «GÜRING», тип ![]() [10], (рис. 1).
[10], (рис. 1).
|
|
|
| |||
| (a) | (б) | (в) | |||
Рис. 1. Три типа заточки сверл: (a) «Классическое 118»; (б) «Крест 118» ; (в) «Крест 135»
1) DIN 338 (HSS – сверло стандартное), заточка с конической задней гранью без уменьшения перемычки, угол при вершине 118° – «Классическое 118».
2) DIN 338 (HSS – свело стандартное), заточка крестом с конической задней гранью, угол при вершине 118°, покрытие TiN – «Крест 118».
3) DIN 345 (M42 – сверло повышенной жесткости, изготовлено из легированной стали CoMo), заточка крестом с конической задней гранью, угол при вершине 135° - «Крест 135».
Обрабатываемый материал - сталь XC 48, σR = 500 ×106 [Pa].Эксперименты проводились в лаборатории института ENSAM в Экс-ан-Провансе, во Франции. Частично результаты данных исследований были доложены на 3rd International Conference on Metal Cutting and High Speed Machining, Metz, France, 2001 [5]. Усилия резания – ![]() – измерялись с помощью платформы «KISTLER», типа 9272, SN 514679 в [N] и [N.m] соответственно. Станок: «Atelier GSP», типа 205 RB. Усилия F и M измерялись в стационарной фазе резания как средние величины на интервале времени в 1с.
– измерялись с помощью платформы «KISTLER», типа 9272, SN 514679 в [N] и [N.m] соответственно. Станок: «Atelier GSP», типа 205 RB. Усилия F и M измерялись в стационарной фазе резания как средние величины на интервале времени в 1с.
Для всех трёх случаев рассматривались две аппроксимации экспериментальных данных в виде законов с двумя постоянными , :
![]() , (35)
, (35)
![]() . (36)
. (36)
Каждое испытание ![]() характеризовалось задаваемой парой чисел
характеризовалось задаваемой парой чисел ![]() (Конечно, скорость резания также фиксировалась, но, согласно принятой гипотезе (23), её влиянием пренебрегалось.) и парой измеряемых значений
(Конечно, скорость резания также фиксировалась, но, согласно принятой гипотезе (23), её влиянием пренебрегалось.) и парой измеряемых значений ![]() . Для определения постоянных g, q предварительно результаты пересчитывались в соответствующие безразмерные комплексы
. Для определения постоянных g, q предварительно результаты пересчитывались в соответствующие безразмерные комплексы ![]() :
:
 . (37)
. (37)
Целевой функцией является среднеквадратичное отклонение от множества экспериментальных точек на плоскости 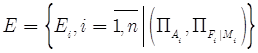 до множества, определяемого соответствующей функцией аппроксимации (рис. 2):
до множества, определяемого соответствующей функцией аппроксимации (рис. 2):
 . (38)
. (38)
В формулах через ![]() обозначено расстояние от точки до множества точек, формирующих линию:
обозначено расстояние от точки до множества точек, формирующих линию:
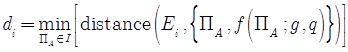 . (39)
. (39)
Коэффициенты g, q определяются из условия минимума целевых функций :
![]() . (40)
. (40)
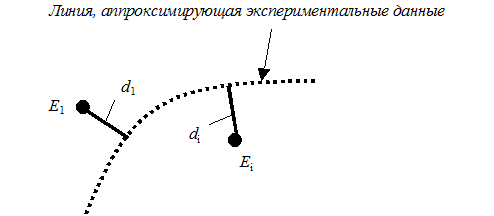
Рис 2 Геометрический смысл аргумента целевой функции
Минимальные значения целевых функций принимаются за меру соответствия между аппроксимацией и экспериментальными данными -
![]() . (41)
. (41)
Меньшим значениям ![]() соответствует лучшая аппроксимация. При численной реализации минимум ищется методом симплексов. Для определения расстояний задаётся интервал изменения аргумента
соответствует лучшая аппроксимация. При численной реализации минимум ищется методом симплексов. Для определения расстояний задаётся интервал изменения аргумента ![]()
 . Значения функции
. Значения функции ![]() вычисляются на дискретном множестве с малым шагом
вычисляются на дискретном множестве с малым шагом ![]() .
.
Ниже изображены результаты вычислений для трёх серий испытаний. Результаты измерений приведены в Приложении 2.
На рис. 3 и 4 представлены экспериментальные данные и аппроксимации в соответствии с двухкоснстантным линейным законом двухконстантным показательным законом для сверла «Классическое 118». Соответствующие зависимости имеют вид
Для линейного закона
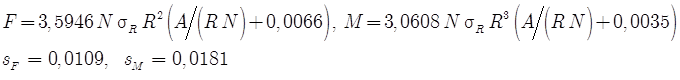 (42)
(42)
и для показательного закона
 (43)
(43)

Рис. 3. Результаты обработки результатов для сверла «Классическое 118» для закона
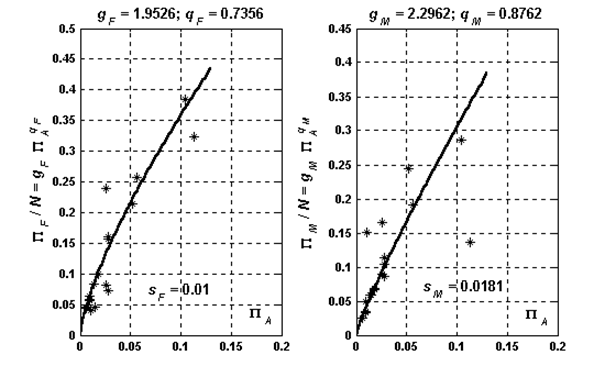
Рис 4 - Результаты обработки результатов для сверла «Классическое 118» для закона
Приближения в обоих случаях аппроксимируют экспериментальные данные примерно одинаково, однако показательный закон лучше приближает зависимость осевой силы: ![]() .
.
На рис. 5, 6 и 7, 8 представлены аналогичные результаты для сверл «Крест 118» и «Крест 135».

Рис. 5. - Результаты обработки результатов для сверла «Крест 118»

Рис. 6. - Результаты обработки результатов для сверла «Крест 118»
Для линейного закона (сверло «Крест 118»)
 (44)
(44)
и для показательного закона
 (45)
(45)
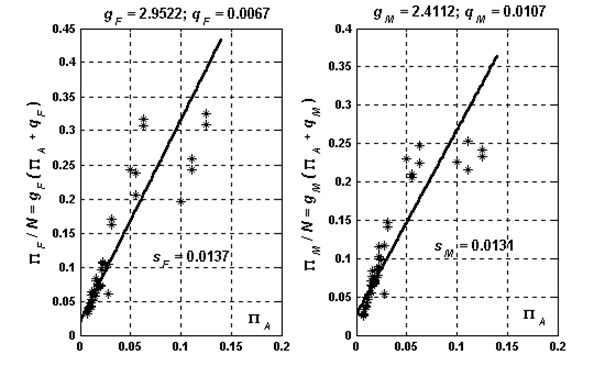
Рис 7 - Результаты обработки результатов для сверла «Крест 135»
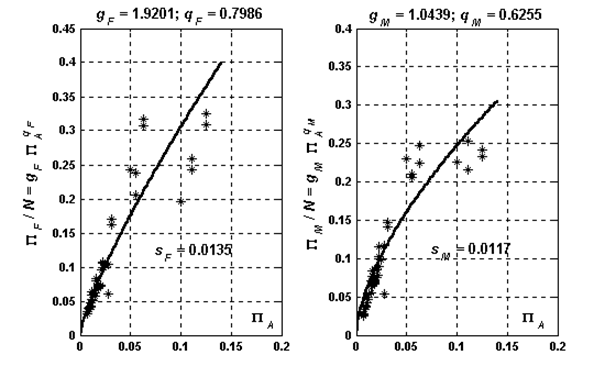
Рис 8 - Результаты обработки результатов для сверла «Крест 118»
Для линейного закона («Крест 135»)
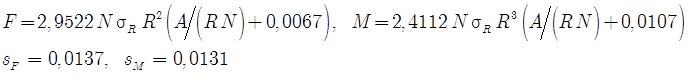 (46)
(46)
и показательного закона
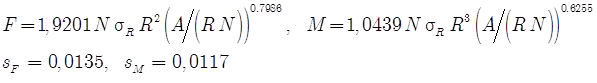 (47)
(47)
На следующих рисунках (рис. 9, 10) для сравнения приведены графики по зависимостям , … . Результаты представлены в одном масштабе.

Рис 9 - Результаты аппроксимации по линейным зависимостям для сверл:
1 - «Классическое 118»; 2 - «Крест 118»; 3 - «Крест 135»
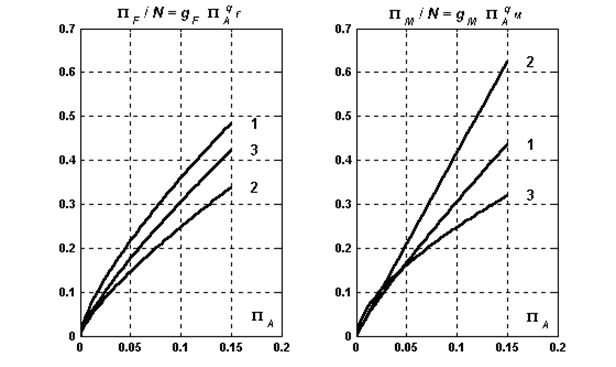
Рис 10 - Результаты аппроксимации по степенным зависимостям :
1 - «Классическое 118»; 2 - «Крест 118»; 3 - «Крест 135».
Следует отметить близость полученных аппроксимаций в безразмерном – критериальном виде. Различия объясняются неодинаковой геометрией и состоянием поверхности инструментов, а также погрешностями измерений.
Наибольшая адекватность при аппроксимации достигнута для второй серии экспериментов ![]() рис. 5, 6.
рис. 5, 6.
Зависимости , … могут быть использованы в любой системе единиц измерения, и, как следствие, их можно применять в любых математических моделях.
Если воспользоваться традиционным представлением зависимостей для сил, то, например, соотношения примут вид ![]()
 (48)
(48)
Естественно, что при этом теряется возможность использования в математических однородных по размерностям моделях. Более того, при обработке экспериментальных данных зависимостями типа увеличивается число определяемых постоянных. В три физические величины ![]() связываются тремя константами
связываются тремя константами ![]() . В соотношение для силы
. В соотношение для силы ![]() связывает пять физических величин двумя константами
связывает пять физических величин двумя константами ![]() . Неизбежные погрешности в экспериментальных данных приводят к погрешностям в определении постоянных в регрессионных зависимостях, однако использование безразмерных критериев в качестве аргументов всегда даёт физически осмысленные соотношения.
. Неизбежные погрешности в экспериментальных данных приводят к погрешностям в определении постоянных в регрессионных зависимостях, однако использование безразмерных критериев в качестве аргументов всегда даёт физически осмысленные соотношения.
5. ФИЗИЧЕСКИ ПОДОБНЫЕ ЯВЛЕНИЯ
Функциональные зависимости между критериями подобия описывают феноменологию изучаемых явлений. Преобразования физических параметров, при которых функциональные соотношения не меняют своих значений, описывают физически идентичные явления, называемые подобными. Такие преобразования соответствуют неизменным значениям критериев подобия
![]() (49)
(49)
Любая математическая модель реального явления не является полной. Поэтому говорить о подобии явлений, согласно , можно только в приближённом смысле.
При создании математической модели исследователь предполагает, что модель выхватывает наиболее существенные стороны явления. В то же время, даже обеспечение соотношений (40) для реальных ситуаций не всегда представляется возможным. Например, если существенным является критерий ![]() и мы хотим получить аналогичные феномены для материалов с различными значениями относительного удлинения при разрушении, то либо подобных явлений не существует, либо критерий
и мы хотим получить аналогичные феномены для материалов с различными значениями относительного удлинения при разрушении, то либо подобных явлений не существует, либо критерий ![]() входит в комбинацию с другими безразмерными комплексами, образуя независимую функциональную переменную, для которой может быть выполнено условие (40).
входит в комбинацию с другими безразмерными комплексами, образуя независимую функциональную переменную, для которой может быть выполнено условие (40).
Примером такой ситуации является следующий результат. В [9] приводятся данные о влиянии скорости резания ![]() и механических свойств стали 100 Cr6 - σR, σy, δ, - на образование стружки при точении. Стружка в "пилообразной" форме появлялась в следующих условиях, (остальные параметры оставались неизменными)
и механических свойств стали 100 Cr6 - σR, σy, δ, - на образование стружки при точении. Стружка в "пилообразной" форме появлялась в следующих условиях, (остальные параметры оставались неизменными)
1) VC = 16,67 [m /s], σR = 1150 [MPa], σy= 1060 [MPa], δ = 0,08.
2) VC = 1,667 [m /s], σR = 1840 [MPa], σy= 1700 [MPa], δ = 0,005.
Даже не зная конкретных законов, описывающих явление, из этих результатов можно извлечь весьма полезную информацию для приложений. Скорость резания входит в критерий подобия ![]() , в то же время, для обоих случаев критерий
, в то же время, для обоих случаев критерий ![]() имеет примерно одинаковые значения:
имеет примерно одинаковые значения:
 (50)
(50)
Анализируя данные, можно заметить, VC↑ ⇔ δ↑: для наблюдения одинаковых феноменов в более пластичных материалах следует увеличить скорость резания. Таким образом, можно сделать следующее предположение, вытекающее из формы критериев подобия :
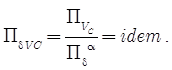 (51)
(51)
Согласно гипотезе можно установить соотношение
 (52)
(52)
То есть, получаем закон для обеспечения подобных условий резания
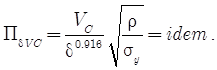 (53)
(53)
Соотношение в широком диапазоне можно обеспечить за счет выбора скорости резания.
Конечно, значение показателя α может быть уточнено. Однако, важным является сам факт возможности получения подобных результатов.
6. АНАЛИЗ И ПЕРСПЕКТИВЫ
Приложение к вибрационному сверлению. В случае переменной толщины снимаемого слоя при симметричном расположении режущих кромок каждая режущая кромка снимает слой ![]() . Соотношения выражают закон резания в квазистатической форме. Этот же закон можно применять до частот колебаний
. Соотношения выражают закон резания в квазистатической форме. Этот же закон можно применять до частот колебаний ![]() . При этом толщину снимаемого слоя, приходящегося на одну режущую кромку, следует заменить на
. При этом толщину снимаемого слоя, приходящегося на одну режущую кромку, следует заменить на ![]() . То есть, для степенной аппроксимации имеем
. То есть, для степенной аппроксимации имеем
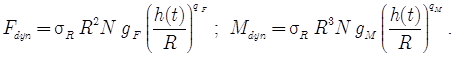 (54)
(54)
Проделаем эквивалентное преобразование
 (55)
(55)
Таким образом, при вибрациях в законе резания следует провести замену ![]() и, в частности, закон резания (45) принимает вид
и, в частности, закон резания (45) принимает вид
![]() (56)
(56)
Понятие жёсткости резания. При анализе вибраций технологической системы удобно ввести по определению коэффициенты жёсткости резания ![]() :
:
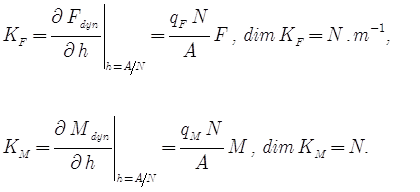 (57)
(57)
Зависимости позволяют выразить силу и момент через соответствующие жёсткости резания
 , (58)
, (58)
а также, переписать законы резания в виде
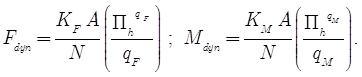 (59)
(59)
Удельная сила резания [11]. Для упрощения оценки усилий резания при сверлении осевая сила и момент представляются в виде
![]() (60)
(60)
Коэффициенты ![]() называются удельной силой резания. В случае степенного закона резания можно получить явную форму для
называются удельной силой резания. В случае степенного закона резания можно получить явную форму для ![]() :
:
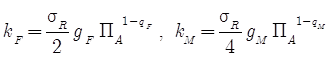 . (61)
. (61)
В случае, если ![]() удельные силы резания не зависят от подачи, что очень часто предполагается неявным образом.
удельные силы резания не зависят от подачи, что очень часто предполагается неявным образом.
Методика перехода от существующих экспериментальных зависимостей к зависимостям, удовлетворяющих принципу однородности размерностей. Следует различать две случая: 1) имеются экспериментальные данные E i : {Ai [m], Ri [m]}, {Fi [N], Mi [N.m]}; 2) имеются зависимости вида (39). В обоих случаях необходимо иметь характеристику прочности обрабатываемого материала типа sR [Pa] чтобы сформировать безразмерные комплексы:
 (62)
(62)
В первом случае обработка проводится так, как это показано в п°4 настоящей работы. Во втором случае информация о множестве экспериментальных точек, породивших соответствующую аппроксимацию, отсутствует. Основная идея предлагаемой методики состоит в том, что имеющаяся зависимость используется для генерации соответствующего множества "экспериментальных данных". При этом возможно добавление искусственно введенного «шума» в расчетные данные. После чего используется описанный выше метод.
Список литературы
- Gouskov A., Brun-Picard D. Instabilité du perçage vibratoire // PRIMECA’96. Nantes, France, 1996.P. 31-38.
- Brun-Picard D., Gouskov A., Lesage D., Vincenti J. Perçage vibratoire par tête auto- vibrante. Approche théorique et premières expérimentations // Deuxième séminaire PPF. Maîtrise globale du procédé d’enlèvement de matière et techniques associées. Aixen –province, France,Jan. 1999. P. 11-22.
- Gouskov A., Brun-Picard D. Dynamique du perçage vibratoire avec pré-serrage unilatéral // Troisième séminaire PPF. Maîtrise globale du procédé d’enlèvement de matière et techniques associées. Angers, France,Mai 1999. P. 56-68.
- Brissaud D., Gouskov A., Paris H., Tichkiewitch S. A more realistic cutting force model at uncut chip thickness close to zero // Annals of the CIRP. 2007. Vol. 56. P. 415-418.
- Gouskov A., Moisan A., Brun-Picard D., Moraru G. Application of the Dimensional Analysis to the Determination of Cutting Forces // 3rd International Conference on Metal Cutting and High Speed Machining, Metz, France, 2001. Vol. 1. P. 35-42.
- Stephenson D. A., Agapiou J. S. Metal Cutting Theory and Practice. New York, Basel, Hong Kong : Marcel Dekker, Inc., 1997. 898 p.
- Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1977. 440 с.
- Masounave J., Maugendre S., Scheed L. Prédiction des efforts de perçage des métaux // Matériaux & Techniques. 1998. № 9-10. P. 7-16.
- Poulachon G., Moisan A.L. A contribution to the Study of the Cutting Mechanisms During High Speed Machining of Hardened Steel // Annals of CIRP. 1998. № 47/1. P. 73-76.
- GÜRING, 93. Outillage de coupe de précision. 977 p.
- Tanguy J.-C. Perçage au foret hélicoïdal. Guide de CETIM. CETIM, 1993. 139 p.
ПРИЛОЖЕНИЕ 1
АЛГОРИТМ ОПРЕДЕЛЕНИЯ КРИТЕРИЕВ ПОДОБИЯ (MATLAB)
format rat % формат арифметики рациональных чисел
nd=4; %число базовых единиц измерения
np=11; %число размерных параметров
% R b A VC sy sR ro l c F M
% 1 2 3 4 5 6 7 8 9 10 11 – номера параметров
% матрица размерностей параметров [уравнение ] :
D=[0 0 0 0 1 1 1 1 0 1 1;
1 1 1 1 -1 -1 -3 1 2 1 2;
0 0 0 -1 -2 -2 0 -3 -2 -2 -2;
0 0 0 0 0 0 0 -1 -1 0 0];
p0=(1:np);P=[];R=[];
for i=1:np-nd+1
for j=i+1:np-nd+2
for k=j+1:np-nd+3
for l=k+1:np-nd+4
p=[i j k l];
if det(D(:,p))~=0
P=[P;p];r=p0;r(p)=[];R=[R;r];
end
end
end
end
end
[a,b]=size(P);
for j=1:a
D1=D(:,P(j,:));D2=-D(:,R(j,:));S=inv(D1)*D2;
DimMatr=[S;eye(np-nd, np-nd)]; [Y,I]=sort([P(j,:)';R(j,:)']);
DimMatr=DimMatr(I,:) %показатели степеней параметров, образующих P
pause
end
Пример расчёта (одна из матриц)

ПРИЛОЖЕНИЕ 2
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
« Классическое 118° » | « Крест 118° » с покрытием | « Крест 135° » | ||||||||||||
d [mm] | A[mm/t] | VC [m/s] | F[kN] | M[Nm] | d [mm] | A[mm/t] | VC [m/s] | F[kN] | M[Nm] | d [mm] | A[mm/t] | VC [m/s] | F[kN] | M[Nm] |
4.4 | 0.045 | 0.207 | 0.192 | 1.598 | 5.9 | 0.045 | 0.386 | 0.257 | 0.760 | 4 | 0.045 | 0.261 | 0.234 | 0.400 |
4.4 | 0.064 | 0.207 | 0.222 | 0.626 | 5.9 | 0.045 | 0.386 | 0.358 | 1.266 | 4 | 0.064 | 0.261 | 0.321 | 0.668 |
4.4 | 0.125 | 0.207 | 0.351 | 1.104 | 5.9 | 0.045 | 0.386 | 0.363 | 1.255 | 4 | 0.090 | 0.261 | 0.423 | 0.919 |
4.4 | 0.250 | 0.207 | 1.248 | 2.037 | 5.9 | 0.064 | 0.386 | 0.682 | 2.036 | 4 | 0.125 | 0.261 | 0.647 | 1.175 |
4.4 | 0.500 | 0.207 | 1.565 | 1.444 | 5.9 | 0.064 | 0.386 | 0.673 | 2.071 | 4 | 0.250 | 0.261 | 1.266 | 1.974 |
4.4 | 0.125 | 0.288 | 0.760 | 1.206 | 5.9 | 0.064 | 0.386 | 0.672 | 1.993 | 4 | 0.500 | 0.261 | 1.236 | 1.929 |
4.4 | 0.125 | 0.414 | 0.772 | 0.919 | 5.9 | 0.125 | 0.386 | 0.539 | 1.795 | 4 | 0.045 | 0.377 | 0.255 | 0.374 |
4.8 | 0.045 | 0.314 | 0.365 | 0.686 | 5.9 | 0.125 | 0.386 | 0.534 | 1.709 | 4 | 0.064 | 0.377 | 0.333 | 0.616 |
4.8 | 0.064 | 0.314 | 0.477 | 0.809 | 5.9 | 0.125 | 0.386 | 0.549 | 1.756 | 4 | 0.090 | 0.377 | 0.428 | 0.822 |
4.8 | 0.125 | 0.314 | 0.465 | 1.241 | 5.9 | 0.125 | 0.556 | 0.512 | 1.739 | 4 | 0.125 | 0.377 | 0.678 | 1.132 |
4.8 | 0.250 | 0.314 | 1.238 | 3.377 | 5.9 | 0.125 | 0.556 | 0.520 | 1.760 | 4 | 0.250 | 0.377 | 1.228 | 1.791 |
4.8 | 0.500 | 0.314 | 2.210 | 3.962 | 5.9 | 0.125 | 0.556 | 0.520 | 1.752 | 4 | 0.500 | 0.377 | 1.303 | 1.864 |
4.8 | 0.125 | 0.452 | 1.379 | 2.281 | 4 | 0.045 | 0.377 | 0.181 | 0.359 | 4.5 | 0.045 | 0.294 | 0.218 | 0.482 |
6.9 | 0.045 | 0.451 | 0.518 | 1.004 | 4 | 0.045 | 0.377 | 0.185 | 0.360 | 4.5 | 0.064 | 0.294 | 0.286 | 0.736 |
6.9 | 0.045 | 0.451 | 0.538 | 1.027 | 4 | 0.045 | 0.377 | 0.188 | 0.371 | 4.5 | 0.090 | 0.294 | 0.364 | 0.970 |
6.9 | 0.045 | 0.451 | 0.546 | 1.019 | 4 | 0.064 | 0.377 | 0.236 | 0.518 | 4.5 | 0.125 | 0.294 | 0.526 | 1.333 |
6.9 | 0.064 | 0.451 | 0.668 | 1.377 | 4 | 0.064 | 0.377 | 0.236 | 0.514 | 4.5 | 0.250 | 0.294 | 1.037 | 2.387 |
6.9 | 0.064 | 0.451 | 0.663 | 1.431 | 4 | 0.064 | 0.377 | 0.231 | 0.489 | 4.5 | 0.500 | 0.294 | 1.312 | 2.881 |
6.9 | 0.064 | 0.451 | 0.689 | 1.431 | 4 | 0.125 | 0.377 | 0.393 | 0.911 | 4.5 | 0.045 | 0.424 | 0.207 | 0.557 |
6.9 | 0.125 | 0.451 | 1.187 | 2.733 | 4 | 0.125 | 0.377 | 0.380 | 0.894 | 4.5 | 0.064 | 0.424 | 0.317 | 0.809 |
6.9 | 0.125 | 0.451 | 1.189 | 2.802 | 4 | 0.125 | 0.377 | 0.391 | 0.902 | 4.5 | 0.090 | 0.424 | 0.373 | 0.863 |
6.9 | 0.125 | 0.451 | 1.180 | 2.805 | 4.5 | 0.045 | 0.424 | 0.217 | 0.424 | 4.5 | 0.125 | 0.424 | 0.306 | 0.613 |
|
|
|
|
| 4.5 | 0.045 | 0.424 | 0.212 | 0.444 | 4.5 | 0.250 | 0.424 | 1.201 | 2.339 |
|
|
|
|
| 4.5 | 0.045 | 0.424 | 0.214 | 0.433 | 4.5 | 0.500 | 0.424 | 1.228 | 2.459 |
|
|
|
|
| 4.5 | 0.125 | 0.424 | 0.414 | 1.093 | 5 | 0.045 | 0.471 | 0.236 | 0.562 |
|
|
|
|
| 4.5 | 0.125 | 0.424 | 0.407 | 1.092 | 5 | 0.064 | 0.471 | 0.321 | 0.832 |
|
|
|
|
| 4.5 | 0.125 | 0.424 | 0.409 | 1.110 | 5 | 0.090 | 0.471 | 0.423 | 1.117 |
|
|
|
|
| 5 | 0.045 | 0.471 | 0.214 | 0.487 | 5 | 0.125 | 0.471 | 0.645 | 1.525 |
|
|
|
|
| 5 | 0.045 | 0.471 | 0.223 | 0.511 | 5 | 0.250 | 0.471 | 1.514 | 3.602 |
|
|
|
|
| 5 | 0.045 | 0.471 | 0.228 | 0.513 | 5 | 0.500 | 0.471 | 1.225 | 3.538 |
|
|
|
|
| 5 | 0.125 | 0.471 | 0.462 | 1.281 | 5.5 | 0.045 | 0.518 | 0.292 | 0.690 |
|
|
|
|
| 5 | 0.125 | 0.471 | 0.457 | 1.325 | 5.5 | 0.064 | 0.518 | 0.398 | 1.038 |
|
|
|
|
| 5.9 | 0.045 | 0.556 | 0.263 | 0.695 | 5.5 | 0.090 | 0.518 | 0.502 | 1.316 |
|
|
|
|
| 5.9 | 0.045 | 0.556 | 0.272 | 0.732 | 5.5 | 0.125 | 0.518 | 0.809 | 1.862 |
|
|
|
|
| 5.9 | 0.045 | 0.556 | 0.275 | 0.748 | 6 | 0.045 | 0.565 | 0.308 | 0.755 |
|
|
|
|
| 5.9 | 0.125 | 0.556 | 0.538 | 1.724 | 6 | 0.064 | 0.565 | 0.430 | 1.136 |
|
|
|
|
| 5.9 | 0.125 | 0.556 | 0.539 | 1.709 | 6 | 0.090 | 0.565 | 0.564 | 1.497 |
|
|
|
|
| 5.9 | 0.125 | 0.556 | 0.532 | 1.735 | 6 | 0.125 | 0.565 | 0.857 | 2.104 |
|
|
|
|
|
|
|
|
|
| 6.8 | 0.045 | 0.445 | 0.366 | 1.019 |
|
|
|
|
|
|
|
|
|
| 6.8 | 0.045 | 0.445 | 0.365 | 1.032 |
|
|
|
|
|
|
|
|
|
| 6.8 | 0.045 | 0.445 | 0.372 | 0.991 |
|
|
|
|
|
|
|
|
|
| 6.8 | 0.064 | 0.445 | 0.469 | 1.467 |
|
|
|
|
|
|
|
|
|
| 6.8 | 0.064 | 0.445 | 0.472 | 1.436 |
|
|
|
|
|
|
|
|
|
| 6.8 | 0.064 | 0.445 | 0.474 | 1.461 |
|
|
|
|
|
|
|
|
|
| 6.8 | 0.125 | 0.445 | 0.869 | 2.667 |
|
|
|
|
|
|
|
|
|
| 6.8 | 0.125 | 0.445 | 0.831 | 2.633 |
|
|
|
|
|
|
|
|
|
| 6.8 | 0.125 | 0.445 | 0.852 | 2.709 |
Публикации с ключевыми словами: сверление, подобие, анализ размерностей, усилия резания, законы поведения при резании
Публикации со словами: сверление, подобие, анализ размерностей, усилия резания, законы поведения при резании
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||






