научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2013
DOI: 10.7463/0813.0585558
УДК 621.74.019
Россия, МГТУ им. Н.Э. Баумана
polyakov.serguei@googlemail.com
1. Введение
Наиболее эффективным расчетным методом прогноза микропористости считается прямое моделирование процесса образования пор при затвердевании на основе использования уравнения Дарси. Однако необходимые для этого математические модели еще недостаточно точны и требуют совершенствования.
На практике применяют различные формы критериев образования пористости. Наиболее популярный из них - критерий Ниямы [1]. Однако необходимо отметить, что одним из главных недостатков имеющихся критериев, в том числе и критерия Ниямы, является отсутствие учета ряда существенных технологических факторов. Некоторые практические результаты улучшения использования критерия Ниямы с учетом технологических факторов приведены в статье [2]. Однако, при работе над статьей, авторам стала ясна ограниченность исходной концепции критерия Ниямы, основанной на упрощенной модели фильтрационного течения в двухфазной зоне, позволяющей только оценивать тенденции влияния технологических параметров на критичекое значения числа Ниямы. Из этого возникла идея построения нового критерия с более совершенной математической моделью, которая бы с исходных формулировок включала параметры технологических факторов и была свободна от необходимости «настройки» с помощью сравнения модельных расчетов и эксперимента. При разработке нового критерия были использованы модели из работ [3, 7], которые были обобщены и адаптированы к условиям настоящего исследования.
Как известно пористость в отливках может проявляется в различной форме, например, междендритной, поверхностной или осевой пористости. Рамки исследований настоящей работы ограничены первым видом пористости.
1. Вывод критерия
Условие образования пористости в произвольной точке ![]() (здесь и далее символ «
(здесь и далее символ «![]() » у переменной означает произвольное, но фиксированное значение, например,
» у переменной означает произвольное, но фиксированное значение, например, ![]() или
или ![]() ) одномерной двухфазной зоны
) одномерной двухфазной зоны![]() (рис. 1) можно представить в форме неравенства Пивоньки - Флемингса [7].
(рис. 1) можно представить в форме неравенства Пивоньки - Флемингса [7].
![]() (1)
(1)
где ![]() - критический перепад давления в точке двухфазной зоны, при котором возникают условия для образования пор;
- критический перепад давления в точке двухфазной зоны, при котором возникают условия для образования пор; ![]() - перепад давления в данной точке расплава.
- перепад давления в данной точке расплава.
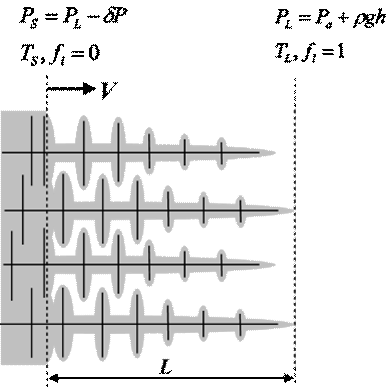
Рис. 1.
Компоненты соотношения (1) вычисляются по формулам ![]() и
и ![]() , где
, где ![]() - давление в расплаве в данной точке, при котором создаются условия для образования пор;
- давление в расплаве в данной точке, при котором создаются условия для образования пор; ![]() - давление в расплаве в данной точке.
- давление в расплаве в данной точке.
На основе неравенства (1) можно построить критерий образования пористости для произвольной точки ![]() двухфазной зоны:
двухфазной зоны:
 (2)
(2)
Если неравенство (2) выполняется - то пористость есть, если не выполняется – пористости нет.
Рассмотрим поведение числителя и знаменателя критерия в пределах двухфазной зоны.
Числитель – критический перепад давления для образования пор
Начиная с работы [7], полагают [2-4,7-9 и др.], что критическое давление ![]() в некоторой точке двухфазной зоны можно определить по формуле:
в некоторой точке двухфазной зоны можно определить по формуле:
![]() , (3)
, (3)
где ![]() - давление газа в кавитационных пузырьках, а
- давление газа в кавитационных пузырьках, а ![]() - капиллярное давление, равное:
- капиллярное давление, равное:
 , (4)
, (4)
здесь ![]() - поверхностное натяжение,
- поверхностное натяжение, ![]() - радиус «жизнеспособного» зародыша поры. С учетом (4) формула (3) принимает вид:
- радиус «жизнеспособного» зародыша поры. С учетом (4) формула (3) принимает вид:
 , (5)
, (5)
а критический перепад давления:
 (6)
(6)
Давление в газовом пузырьке металлических жидкостей зависит от скорости диффузии газа из жидкости в пузырек. При высокой скорости диффузии и известном законе состояния газа в пузырьке, газовое давление в пузырьке можно выразить через его радиус: ![]() . Однако величина
. Однако величина ![]() для металлических жидкостей, как правило, неизвестна.
для металлических жидкостей, как правило, неизвестна.
В настоящей работе предлагается отказаться от использования конкретного значения величины ![]() , а сделать ее оценку по расстоянию между вторичными ветвями дендритов. Для этого будем исходить из допущения, что для микропоры, возникающей в расплаве, в сетке вторичных ветвей дендритов должно быть некоторое свободное пространство, где эта микропора может возникнуть. Это свободное пространство характеризуется размером
, а сделать ее оценку по расстоянию между вторичными ветвями дендритов. Для этого будем исходить из допущения, что для микропоры, возникающей в расплаве, в сетке вторичных ветвей дендритов должно быть некоторое свободное пространство, где эта микропора может возникнуть. Это свободное пространство характеризуется размером ![]() , т.е. радиусом шара, вписанного в жидкую часть междендритного пространства между вторичных ветвей дендритов, рис. 2.
, т.е. радиусом шара, вписанного в жидкую часть междендритного пространства между вторичных ветвей дендритов, рис. 2.

Рис. 2.
Другими словами, если в двухфазной зоне возникает «жизнеспособный» критический зародыш микропоры, то для него справедливо условие ![]() . С учетом принятого соотношения для радиуса микропоры, критический перепад давления будет равен:
. С учетом принятого соотношения для радиуса микропоры, критический перепад давления будет равен:
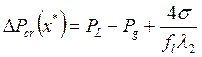 (7)
(7)
Следует еще раз отметить особенность формулировки критического значения ![]() по выражению (7). Если в жидкой фазе без дендритов критический радиус
по выражению (7). Если в жидкой фазе без дендритов критический радиус ![]() , то сетка дендритов создает геометрические ограничения, при которых кавитационный радиус не может превышать
, то сетка дендритов создает геометрические ограничения, при которых кавитационный радиус не может превышать ![]() . Следовательно, можно принять
. Следовательно, можно принять ![]() и выражение (7) вполне корректно для использования в критерии образования пористости в форме (2). Однако, если
и выражение (7) вполне корректно для использования в критерии образования пористости в форме (2). Однако, если ![]() , получается критерий образования пористости в точке двухфазной зоны с некоторым «запасом». Ясно, что этот «запас» стремится к нулю на фронте затвердевания, т.к.
, получается критерий образования пористости в точке двухфазной зоны с некоторым «запасом». Ясно, что этот «запас» стремится к нулю на фронте затвердевания, т.к. ![]() стремится здесь так же к нулю. Таким образом, использование выражения (7) в критерии образования газо-усадочной пористости в формуле (2), можно считать оправданным при любом соотношении
стремится здесь так же к нулю. Таким образом, использование выражения (7) в критерии образования газо-усадочной пористости в формуле (2), можно считать оправданным при любом соотношении ![]() и
и ![]() . Эта особенность предлагаемого подхода является полезной в практических расчетах, учитывая почти полное отсутствие информации о
. Эта особенность предлагаемого подхода является полезной в практических расчетах, учитывая почти полное отсутствие информации о ![]() для литейных сплавов.
для литейных сплавов.
Знаменатель - перепад давления в расплаве
Для описания фильтрационного течения расплава в одномерной двухфазной зоне используется уравнение фильтрации Дарси:
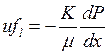 (8)
(8)
где ![]() – скорость фильтрации,
– скорость фильтрации, ![]() - доля жидкой фазы,
- доля жидкой фазы, ![]() - динамическая вязкость,
- динамическая вязкость,  коэффициент фильтрации по Карман - Козени [5,6],
коэффициент фильтрации по Карман - Козени [5,6], ![]() - расстояние между осями вторичных дендритов (рис. 2).
- расстояние между осями вторичных дендритов (рис. 2).
Из уравнения сохранения массы для одномерной стационарной двухфазной области следует:
![]() (9)
(9)
где ![]() - скорость фронта кристаллизации (рис. 1);
- скорость фронта кристаллизации (рис. 1); ![]() - коэффициент объемной усадки,
- коэффициент объемной усадки, ![]() и
и ![]() - плотность твердой и жидкой фаз.
- плотность твердой и жидкой фаз.
Подставив (9) в (8) получим:
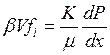 (10)
(10)
Разделяя переменные и интегрируя (10) по ![]() от
от ![]() до
до ![]() , получим искомый перепад давления в точке
, получим искомый перепад давления в точке ![]() :
:
 (11)
(11)
Перейдя к безразмерной температуре ![]() , где
, где ![]() и заменяя переменную
и заменяя переменную ![]() на
на ![]() и предполагая, что
и предполагая, что ![]() постоянны в пределах двухфазной зоны, а
постоянны в пределах двухфазной зоны, а ![]() - средний градиент температуры, получим:
- средний градиент температуры, получим:
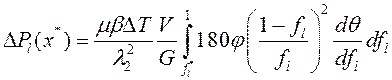 (12)
(12)
где 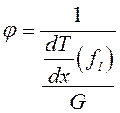 - обратная величина относительного (относительно среднего) градиента. При линейном распределении температурного поля в двухфазной зоне
- обратная величина относительного (относительно среднего) градиента. При линейном распределении температурного поля в двухфазной зоне ![]() .
.
Обозначим интеграл в правой части:
 (13)
(13)
Тогда соотношение (12) можно записать в виде:
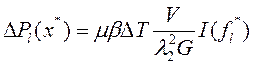 (14)
(14)
и с учетом (14) и (7), новый критерий образования пористости (2) в любой точке стационарной двухфазной зоны принимает вид:
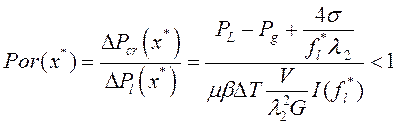 (15)
(15)
Выполнение неравенства (15) хотя бы для одной точки стационарной двухфазной зоны приводит к образованию пористости.
2. Анализ критерия
Для удобства анализа умножим числитель и знаменатель (15) на ![]() и представим (15) в эквивалентной форме:
и представим (15) в эквивалентной форме:
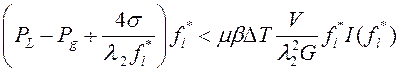 (16)
(16)
В общем случае доля жидкой фазы нелинейно зависит от температуры, что усложняет вычисление интеграла ![]() . Для упрощения вычислений, как это часто делают, примем линейное приближение температуры от доли жидкой фазы и линейное распределение температуры в двухфазной зоне. Тогда в пределах двухфазной зоны имеем:
. Для упрощения вычислений, как это часто делают, примем линейное приближение температуры от доли жидкой фазы и линейное распределение температуры в двухфазной зоне. Тогда в пределах двухфазной зоны имеем:
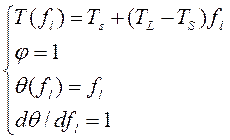 (17)
(17)
Теперь интеграл (13) с учетом (17) можно вычислить аналитически:
 (18)
(18)
а перепад давления (14) с учетом (18) будет равен:
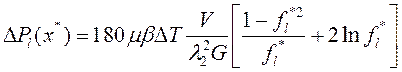 (19)
(19)
Учитывая давление на ликвидусе ![]() , получим эквивалентную форму неравенства (16), пригодную для анализа:
, получим эквивалентную форму неравенства (16), пригодную для анализа:
 (20)
(20)
Правая часть неравенства (20) изменяется от 1 до 0 и представляет собой монотонно убывающую выпуклую вниз функцию (кривая 1 на рис. 3 и 4). Левая часть представляет собой график прямой.
Если график функции в правой части фиксирован и зависит только от доли жидкой фазы, то график прямой в левой части может иметь разный наклон и разную высоту по оси ординат в зависимости от значения технологических параметров и физических свойств сплава. Таким образом, взаимное расположение графика левой и правой частей неравенства (20) отражает в графической форме влияние технологических и физичеких параметров на образование микропористости.
Рассмотрим варианты поведения прямой.
Прежде всего, в зависимости от знака выражения ![]() , угловой коэффициент прямой будет положительным (рис. 3) или отрицательным (рис. 4).
, угловой коэффициент прямой будет положительным (рис. 3) или отрицательным (рис. 4).
В случае малого газового давления (малой газонасыщенности сплава), при ![]() (рис. 3), графики левой и правой частей (20) могут или не пересекаться вообще (прямые 3 и 4), что означает отсутствие условий для образования пористости во всей двухфазной зоне, или могут пересекаться в одной точке (прямая 2). В последнем случае будет образовываться пористость.
(рис. 3), графики левой и правой частей (20) могут или не пересекаться вообще (прямые 3 и 4), что означает отсутствие условий для образования пористости во всей двухфазной зоне, или могут пересекаться в одной точке (прямая 2). В последнем случае будет образовываться пористость.

Рис. 3.
Для того чтобы пористость не возникла, график прямой должен иметь пересечение с осью ординат в точке, значение которой определяется неравенством  (кривые 3 и 4 на рис. 3.). Данное решение получено из левой части (20) при
(кривые 3 и 4 на рис. 3.). Данное решение получено из левой части (20) при ![]() .
.
Если расплав сильно газонасыщен (![]() ), то прямая левой части (20) будет иметь отрицательный наклон (рис. 4, кривые 2, 3, 4).
), то прямая левой части (20) будет иметь отрицательный наклон (рис. 4, кривые 2, 3, 4).

Рис. 4.
Также как и на рис. 3, графики левой и правой частей (20) могут или не пересекаться вообще (прямые 3 и 4), что означает отсутствие условий для образования пористости во всей двухфазной зоне, или могут пересекаться в одной точке (прямая 2).
Для отсутствия пористости достаточно, чтобы график прямой был выше кривой 1 в точках ![]() и
и ![]() (из-за выпуклости вниз кривой 1). Для точки
(из-за выпуклости вниз кривой 1). Для точки ![]() искомое значение уже найдено:
искомое значение уже найдено:  . Для точки
. Для точки ![]() из левой части (20) нетрудно получить условие
из левой части (20) нетрудно получить условие  .
.
Следовательно, новый критерий образования микропористости при линейных допущениях (17) может быть сформулирован так: микропористость будет образовываться в двухфазной зоне, если выполняется хотя бы одно из условий:
 или
или  .
.
В более компактной формулировке новый критерий образования микропористости имеет следующий вид:
![]()
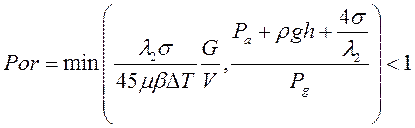 (21)
(21)
Подчеркнем, что полученный критерий не содержит фиксированного значения кавитационного радиуса пузырька. Вместо этого используется геометрическое условие, ограничивающее размеры возможного пузырька в жидкой фазе, содержащейся в пространстве между вторичными осями дендритов.
3. Обсуждение
В случае малой газонасыщенности расплава ![]() значение критерия на фронте затвердевания однозначно определяет условия образования пористости во всей двухфазной зоне. Если
значение критерия на фронте затвердевания однозначно определяет условия образования пористости во всей двухфазной зоне. Если ![]() , то пористости не будет во всей двухфазной зоне.
, то пористости не будет во всей двухфазной зоне.
При высокой газонасыщенности сплава ![]() для отсутствия в двухфазной зоне микропористости уже необходимо выполнение двух условий при нулевом и единичном значении доли жидкой фазы:
для отсутствия в двухфазной зоне микропористости уже необходимо выполнение двух условий при нулевом и единичном значении доли жидкой фазы: ![]() и
и ![]() .
.
Заметим, что второе условие - условие отсутствия микропористости на ликвидусе, т.е. при ![]() , когда твердой фазы еще нет, требует пояснений.
, когда твердой фазы еще нет, требует пояснений.
Известно, что перемещение жидкой фазы в двухфазной зоне по фильтрационной модели начинается со значения доли жидкой фазы, меньше некоторого критического значения ![]() , например, для алюминиевых сплавов во многих экспериментах установлено значение
, например, для алюминиевых сплавов во многих экспериментах установлено значение ![]() [10]. Таким образом, условие при единичном значении доли жидкой фазы правильнее переписать в виде
[10]. Таким образом, условие при единичном значении доли жидкой фазы правильнее переписать в виде ![]() . С математической точки зрения условие
. С математической точки зрения условие ![]() является более жестким ограничением для отсутствия пористости, т.е. если это условие выполняется, то тем более будет выполняться условие
является более жестким ограничением для отсутствия пористости, т.е. если это условие выполняется, то тем более будет выполняться условие ![]() . Условие
. Условие ![]() может быть полезно для оценки образования пористости в отливках из сплавов, где величина
может быть полезно для оценки образования пористости в отливках из сплавов, где величина ![]() еще неизвестна.
еще неизвестна.
Отметим еще одну особенность. В частном случае при постоянной скорости фронта затвердевания ![]() и выполнении условий (17) время
и выполнении условий (17) время ![]() нахождения точки отливки в двухфазной зоне будет
нахождения точки отливки в двухфазной зоне будет ![]() . Соответственно скорость охлаждения
. Соответственно скорость охлаждения 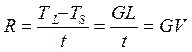 . Если в (21)выразить
. Если в (21)выразить ![]() , то в новом критерии (21) появится хорошо известный критерий (лучше сказать число) Ниямы
, то в новом критерии (21) появится хорошо известный критерий (лучше сказать число) Ниямы ![]() :
:
 (22)
(22)
Последнее выражение позволяет провести анализ области применимости критерия Ниямы в приближение ![]() .
.
Итак, в случае малой газонасыщенности расплава, т.е. при ![]() , для отсутствия пористости достаточно выполнения только одного условия:
, для отсутствия пористости достаточно выполнения только одного условия: 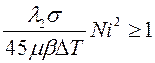 , которое можно переписать в виде:
, которое можно переписать в виде:
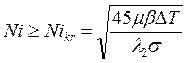 (23)
(23)
При этом атмосферное давление, металлостатическое давление и давление газа в этом условии отсутствуют, и образование пористости будет зависеть только от одной переменной - числа Ниямы (приближенно считаем ![]() ). В теории подобия это интерпретируется как выпадение факторов влияния (атмосферного давления, давления газа и металлостатического давления).
). В теории подобия это интерпретируется как выпадение факторов влияния (атмосферного давления, давления газа и металлостатического давления).
Кроме того, из полученного условия можно определить критическое значение числа Ниямы, выше которого пористость в отливках образовываться не будет.
При высокой газонасыщенности сплава, т.е. при ![]() , значение числа Ниямы выше критического, по новому критерию уже не будет соответствовать условию отсутствия порообразования. Микропористость будет образовываться, если
, значение числа Ниямы выше критического, по новому критерию уже не будет соответствовать условию отсутствия порообразования. Микропористость будет образовываться, если  вне зависимости от числа Ниямы, т.к. прямая левой части неравенства (20) будет пересекать кривую 1 (см. рис. 4, прямая 2). Влияние числа Ниямы на образование пористости сохраняется при высокой газонасыщенности, только для ситуации, при которой
вне зависимости от числа Ниямы, т.к. прямая левой части неравенства (20) будет пересекать кривую 1 (см. рис. 4, прямая 2). Влияние числа Ниямы на образование пористости сохраняется при высокой газонасыщенности, только для ситуации, при которой 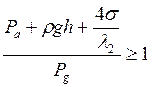 .
.
4. Основные выводы
- Получен новый критерий образования микропористости в отливках. Критерий имеет безразмерную форму и учитывает не только термические условия процесса затвердевания, но и значимые технологические параметры, такие как атмосферное и металлостатическое давление и газонасыщенность сплава.
- Показано, что для условия образования микропористости вместо значения радиуса критического зародыша поры можно использовать его оценку, определяемую через расстояние между вторичными осями дендритов и доли жидкой фазы. Это позволяет отказаться от технически сложного экспериментального определения радиуса критического зародыша микропоры в металлических сплавах.
- Предложена оригинальная схема анализа условия образования пористости на основе графической интерпретации модельных неравенств, позволяющая наглядно представить влияние термических и технологических параметров.
- Полученный критерий не содержит трудно измеряемых физических параметров и не требует «экспериментальной» настройки, что полезно для практического использования в системах моделирования литейных процессов при оценке условий образования микропористости в отливках.
Послесловие к статье. В настоящей статье авторы изложили только краткое описание идей приводящих к новой формы критерия образования пористости. Использование довольно сильных предположений о распределении температурного поля и доли жидкой фазы в двухфазной зоне G=const, (19) может быть снято без изменения основных результатов работы. Более широкое представление о возможностях нового критерия, математические обстоятельства и некоторые идеи его дальнейшего развития для эвтектических сплавов вы найдете на сайте авторов http://newcompcast.ru/. Там же вы можете оставить все ваши замечания и пожелания.
Список литературы
1. Niyama E., Uchida T., Morikawa M., Saito S. A Method of Shrinkage Prediction and its Application to Steel Casting Practice // AFS International Cast Metals Journal. 1982. Vol. 7, no. 3. P. 52-63.
2. Поляков С., Коротченко А.Ю., Баст Ю. Новая форма критерия Нияма для предсказания пористости при затрудненной усадке отливок из Al-Cu сплавов // Литейщик России. 2012. № 4. С. 23-30.
3. Carlson K.D., Beckermann C. Prediction of Shrinkage Pore Volume Fraction Using a Dimensionless Niyama Criterion //Metallurgical and Materials Transactions A. 2009. Vol. 40A. P. 163-175.
4. Pequet Ch., Gremaud M., Rappaz M. Modeling of Microporosity, Macroporosity, and Pipe-Shrinkage Formation during the Solidification of Alloys. Using a Mushy - Zone Refinement Method: Applications to Aluminum Alloys // Metallurgical and Materials Transactions A. 2002. Vol. 33A. P. 2095-2106.
5. Kozeny J. Ueber kapillare Leitung des Wassers im Boden // Sitzungsber Akad. Wiss., Wien, 1927. Vol 136 (2a). P. 271-306.
6. Carman P.C. Fluid flow through granular beds // Transactions, Institution of Chemical Engineers, London, 1937. Vol. 15. P. 150-166.
7. Piwonka T.S., Flemings M.C. Pore Formation in Solidification // TMS-AIME. 1966. Vol. 236. P. 1157-1165.
8. Баландин Г.Ф. Основы теории формирования отливки. Часть II. М.: Машиностроение, 1979. 335 с.
9. Campbell J. Complete Casting. Oxford, 2011. 1130 p.
10. Nielsen O., Arnberg L., Mo A., Thevik H. Mushy zone permeability and grain morphology in equiaxed aluminum-copper alloys // Metallurgical and Materials Transactions A. 1999. Vol. 30A. P. 2455-2462.
Публикации с ключевыми словами: двухфазная зона, критерий микропористости, оценка пористости, закон Дарси, фильтрация расплава, критерий Ниямы
Публикации со словами: двухфазная зона, критерий микропористости, оценка пористости, закон Дарси, фильтрация расплава, критерий Ниямы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



