научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2013
DOI: 10.7463/0613.0574314
УДК 531, 53.072, 62-5, 617-089, 617-7
Россия, МГТУ им. Н.Э. Баумана
Введение
История роботизированной хирургии насчитывает уже более двадцати пяти лет. С каждым годом роботизированная медицина получает все большее распространение. Однако робототехнические комплексы – дорогостоящая продукция. Поэтому, чем больший спектр хирургических операций может выполнить роботизированная система, тем выгоднее ее приобретение.
С целью создания отечественного хирургического комплекса, не уступающего по характеристикам зарубежным аналогам, в рамках федеральной целевой научно-технической программы разрабатывается многофункциональный манипулятор для роботоассистенции в высокоточной хирургии (далее Робот-Манипулятор). Ожидается, что стоимостные показатели разрабатываемого Робота-Манипулятора будут ниже, чем у получивших широкое распространение современных роботизированных комплексов, что сделает возможным его приобретение специализированными и широкопрофильными медицинскими учреждениями [1].
Робот-Манипулятор предназначен для общей хирургии, к которой не относят процедуры, требующие исключительной точности позиционирования инструмента, как, например, задачи нейрохирургии. Применение Робота-Манипулятора для проведения той или иной операции определяется его возможностью точного наведения хирургического инструмента. В попытке расширить предполагаемый спектр выполняемых Роботом-Манипулятором задач, работа посвящена изучению проблемы точности позиционирования хирургического инструмента. Нейрохирургической операцией, требующей высокой точности попадания инструмента в точку цели является биопсия головного мозга. Биопсия – это обязательный метод подтверждения диагноза при подозрении на наличие онкологических заболеваний, при котором проводится прижизненный забор клеток или тканей из организма [2]. Для робота-ассистента процесс подведения инструмента к месту дальнейших манипуляций одинаков, независимо от вида процедуры. Поэтому исследование проблемы позиционирования инструмента реализуем на примере биопсии мозга. Изучение биопсии мозга проведено в условиях реальной операции, проведенной в НИИ нейрохирургии имени Н.Н. Бурденко РАМН, и представлено в работе [3].
Задача позиционирования в общем смысле – одна из основных задач робототехники. Высокая точность позиционирования – требование, предъявляемое ко всем роботизированным системам хирургического вмешательства, поскольку речь идет о безопасном проведении процедуры для пациента. Обзор литературы показывает, что моделирование движения инструмента по заданной траектории методом вычисления управляющих моментов дает хорошие результаты [4-8]. Согласно работам [5, 6, 9] задачу управления удобно решать в среде MATLAB®Simulink. Исследование [10] отдельно посвящено подбору коэффициентов усиления системы управления. Влияние коэффициентов на поведение системы показано, в том числе, в работе [11]. В работе [9] проведено моделирование движения инструмента по заданной траектории в MATLAB®Simulink, однако, без учета управления. Выбор оптимальной траектории движения манипулятора с избыточным числом степеней подвижности представлен в работе [12]. В исследовании [13] предложена методика расчета, позволяющая прокладывать траекторию движения Робота-Манипулятора с учетом минимизации возможных паразитных отклонений инструмента. Разработка схемы управления роботом-манипулятором PUMA 260 приведена в работе [14]. Настоящая работа представляет собой изучение возможности разрабатываемого Робота-Манипулятора позиционировать инструмент при отработке траектории от точки к точке с точностью не менее 0,05 мм. Такую точность хирургического вмешательства в настоящий момент способна обеспечить нейрохирургическая система последнего поколения – робот-ассистент ROSA (Medtech, France) [15].
В первой части представлены исходные данные и допущения, принятые для решения поставленной задачи. Вторая часть включает в себя теорию и моделирование этапов исследования разрабатываемого Робота-Манипулятора. Подразделы описывают: кинематику Робота-Манипулятора, планирование траектории и симуляцию движения по траектории, расчет конфигураций манипулятора для реализации движения вдоль траектории от точки к точке, скорость движения инструмента, оценку показателя манипулятивности и анализ сингулярностей Робота-Манипулятора, динамику и реализацию задачи управления. Третья часть посвящена обсуждению результатов исследования и общим выводам по работе.
Цель исследования. Реализовать численное моделирование задачи позиционирования инструмента семистепенного хирургического Робота-Манипулятора в каждой заданной точке требуемой траектории движения. Погрешность позиционирования инструмента не должна превыщать 0,05 мм.
1 Расчетная схема
Исполнительная кинематическая цепь Робота-Манипулятора представляет собой семь последовательно соединенных между собой с помощью вращательных кинематических пар подвижных звеньев, первое из которых соединено с неподвижным звеном [1]. Для описания связей между соседними звеньями Робота-Манипулятора используется представление Денавита-Хартенберга. Каждое звено характеризуется четырьмя параметрами: постоянными ![]() ,
, ![]() ,
, ![]() и переменной обобщенной координатой
и переменной обобщенной координатой ![]() [4]. Каждое сочленение имеет в своем составе сервопривод, подобранный исходя из требуемого расчетного момента [1]. Характеристиками привода являются передаточное число, масса и моменты инерции. Трение в двигателях и сочленениях не учитывается.
[4]. Каждое сочленение имеет в своем составе сервопривод, подобранный исходя из требуемого расчетного момента [1]. Характеристиками привода являются передаточное число, масса и моменты инерции. Трение в двигателях и сочленениях не учитывается.
Хирургическим инструментом Робота-Манипулятора, согласно проведенной в НИИ нейрохирургии имени Н.Н. Бурденко РАМН операции, является биопсийная игла длиной 200 мм и весом 100 г.
Рабочей средой инструмента является головной мозг. Инструмент воспринимает нагрузки от взаимодействия с тканью. Мозг состоит преимущественно из клеток, называемых серым веществом, и из нервных волокон – белым веществом, так что нагрузки на инструмент незначительны. Поэтому задача позиционирования решается без учета внешних нагрузок на инструмент.
2 Теория и моделирование
2.1 Кинематика Робота-Манипулятора
Используя возможности MATLAB® RoboticsToolbox, создаем Робот-Манипулятор, задав последовательность элементарных поворотов и перемещений [4]. Полученный манипулятор ManRoс инструментом длиной ![]() м в начальном положении изображен на рисунке 1а в виде набора из семи шарниров, соединенных жесткими звеньями. Последнее звено - инструмент изображается связанной с ним системой координат с осью
м в начальном положении изображен на рисунке 1а в виде набора из семи шарниров, соединенных жесткими звеньями. Последнее звено - инструмент изображается связанной с ним системой координат с осью ![]() , направленной вдоль инструмента. На рисунке 1б представлена произвольная конфигурация Робота-Манипулятора.
, направленной вдоль инструмента. На рисунке 1б представлена произвольная конфигурация Робота-Манипулятора.


а) б)
Рисунок 1 – Схема Робота-Манипулятора с инструментом в MATLAB® RoboticsToolbox: а) начальная конфигурация; б) произвольная конфигурация
Известны два типа задач кинематики: прямая и обратная [1].
Прямая задача кинематики: для конкретного манипулятора по известному вектору присоединенных углов - обобщенных координат ![]() , - определить положение и ориентацию инструмента манипулятора относительно абсолютной системы координат
, - определить положение и ориентацию инструмента манипулятора относительно абсолютной системы координат ![]() . Параметры
. Параметры ![]() имеют смысл координат начала системы координат в абсолютной системе отсчета
имеют смысл координат начала системы координат в абсолютной системе отсчета ![]() , а параметры
, а параметры ![]() – углы, задающие ориентацию системы координат
– углы, задающие ориентацию системы координат ![]() относительно
относительно ![]() .
.
Обратная задача кинематики: по заданному положению и ориентации инструмента манипулятора ![]() или
или ![]() найти вектор обобщенных координат
найти вектор обобщенных координат ![]() , где
, где ![]() - матрица однородных преобразований.
- матрица однородных преобразований.
Для моделирования движения по заданной траектории необходимо решать обе задачи.
2.2 Траектория Робота-Манипулятора
При выполнении биопсии мозга местоположение точки цели, располагающейся в глубине мозга, определяется по КТ/МРТ (компьютерная томография/магнитно-резонансная томография) снимкам с помощью специальной компьютерной программы либо стереотаксической системы, либо роботизированной системы, которая рассчитывает координаты искомой точки. После этого хирург планирует траекторию движения Робота-Манипулятора. Учитывая функциональные зоны мозга, которые не должны подвергаться хирургическому воздействию, хирург прокладывает максимально безопасную траекторию движения инструмента к заданной точке [13].
Производить расчет траектории позволяет нейронавигационная система [13]. Траектория в пространстве представляет собой набор точек с известными декартовыми координатами. В программном пакете формируем прямолинейную траекторию движения иглы, задав координаты точек (используется синтаксис программной среды MATLAB):
X = 0.18:0.005:0.23;
Y = 0.30:0.005:0.35;
Z = 0.50:0.005:0.55;
Для сокращения времени расчетов выбран умеренный шаг дискретизации траектории на узловые точки. Полученная траектория в пространстве и в проекциях на плоскости приведена на рисунке 2. Черной звездочкой обозначена начальная точка, а красной – конечная точка траектории.
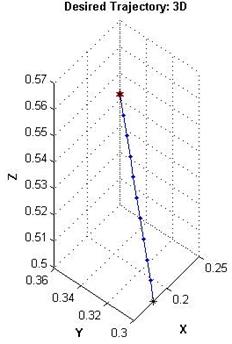
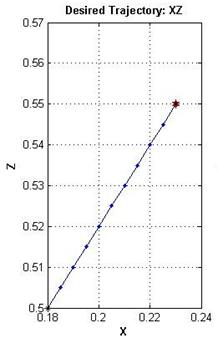
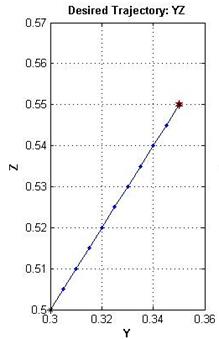
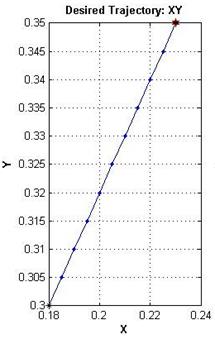
Рисунок 2 – Требуемая траектория в пространстве (сверху-слева), и в проекциях на координатные плоскости
Для Робота-Манипулятора отработка траектории состоит в переходе из одной конфигурации в другую. Определив траекторию в абсолютном пространстве необходимо осуществить преобразование декартовых координат узловых точек в соответствующие присоединенные координаты Робота-Манипулятора. Для этого в каждой узловой точке формируем матрицу однородных преобразований, несущую информацию, как о положении, так и об ориентации инструмента.
Ориентация инструмента не должна быть произвольной. Для обеспечения безопасного прохождения траектории инструмент должен двигаться точно по прямой, соединяющей точки траектории. При проведении биопсии мозга траектории движения могут быть только прямолинейными. Если говорить о произвольных криволинейных траекториях, инструмент должен подходить по касательной к каждой точке. Учитывая высокую дискретизацию навигационной системы, прямую, соединяющую две точки, считаем касательной ко второй точке. На рисунке 3 изображено движение инструмента (красная прямая) по касательной к узловым точкам произвольной криволинейной траектории (синяя кривая).


Рисунок 3 – Симуляция движения инструмента (красная прямая) по траектории (синяя кривая) в разные моменты времени
Формируя матрицу однородных преобразований, учитываем требуемую ориентацию инструмента. Присоединенные координаты сочленений Робота-Манипулятора ![]() получим, решив обратную задачу кинематики [4]. Зная траекторию движения инструмента в присоединенных координатах сочленений, движение инструмента реализуем задавая конфигурацию Робота-Манипулятора в
получим, решив обратную задачу кинематики [4]. Зная траекторию движения инструмента в присоединенных координатах сочленений, движение инструмента реализуем задавая конфигурацию Робота-Манипулятора в ![]() -ой точке, конфигурацию в
-ой точке, конфигурацию в ![]() -ой точке и желаемое количество шагов по времени [4]. На рисунке 4 изображен Робот-Манипулятор в некоторый момент времени отрабатывания траектории.
-ой точке и желаемое количество шагов по времени [4]. На рисунке 4 изображен Робот-Манипулятор в некоторый момент времени отрабатывания траектории.

Рисунок 4 – Движение Робота-Манипулятора по заданной траектории
Изменение присоединенных координат сочленений и декартовых координат конца инструмента во времени приведено на рисунке 5.

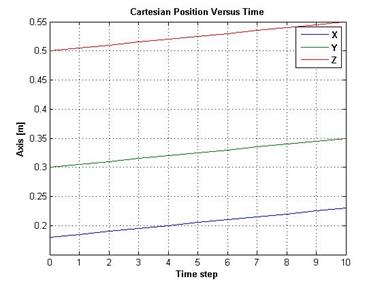
Рисунок 5 – Присоединенные координаты сочленений во времени (слева), декартовые координаты во времени (справа)
Траектория манипулятора из одной конфигурации в другую в пространстве сочленений есть гладкая функция времени, описываемая полиномом пятой степени. Перемещение инструмента в плоскости ![]() изображено на рисунке 6а, что полностью соответствует проекции на плоскость
изображено на рисунке 6а, что полностью соответствует проекции на плоскость ![]() рисунка 2. Ориентация инструмента в углах крена-тангажа-рысканья изображена на рисунке 6б. Изменение углов не наблюдается. Прямые – гладкие.
рисунка 2. Ориентация инструмента в углах крена-тангажа-рысканья изображена на рисунке 6б. Изменение углов не наблюдается. Прямые – гладкие.


а) б)
Рисунок 6 – а) Проекция на плоскость ![]() траектории, отработанной в процессе симуляции движения; б) изменение углов крена-тангажа-рысканья за время симуляции движения
траектории, отработанной в процессе симуляции движения; б) изменение углов крена-тангажа-рысканья за время симуляции движения
2.3 Скорость Робота-Манипулятора
Перемещая конец инструмента из произвольной точки в желаемую, решением обратной задачи кинематики получаем не только присоединенные координаты сочленений на каждом шаге по времени, но и необходимые скорости и ускорения сочленений [5]. Граничные условия для скорости и ускорения, как правило, в начальной и конечной точке нулевые [4, 5, 16]. Для реализации движения через произвольное количество точек, скорость в ![]() -ой точке интервала
-ой точке интервала ![]() будет начальной для интервала
будет начальной для интервала ![]() [5]. И только в самой первой точке траектории и точке цели скорость и ускорение инструмента должны быть равны нулю.
[5]. И только в самой первой точке траектории и точке цели скорость и ускорение инструмента должны быть равны нулю.
Скорость инструмента в абсолютном пространстве определяется вектором [5].
![]()
Введение иглы в мозг при проведении биопсии мозга осуществляется на очень низкой скорости ![]() . В общем случае, скорость введения инструмента в биологическую ткань играет существенную роль при выполнении той или иной хирургической процедуры. Это связно с тем, что биологическая ткань – нелинейный, неоднородный, анизотропный и вязкоупругий материал. При введении иглы в ткань игла воспринимает нагрузки, а ткань деформируется [17]. В лабораториях по всему миру проводятся исследования реологических свойств биологических тканей и влияния скорости введения иглы на точность проведения операции. В некоторых разработках предлагается динамически возбуждать иглу при введении в ткань [18]. Это приводит к снижению силы трения и упрощает процесс разрезания ткани при прокалывании. Пусть скорость поступательного движения инструмента в декартовых координатах равна 0,006 м/с вдоль оси
. В общем случае, скорость введения инструмента в биологическую ткань играет существенную роль при выполнении той или иной хирургической процедуры. Это связно с тем, что биологическая ткань – нелинейный, неоднородный, анизотропный и вязкоупругий материал. При введении иглы в ткань игла воспринимает нагрузки, а ткань деформируется [17]. В лабораториях по всему миру проводятся исследования реологических свойств биологических тканей и влияния скорости введения иглы на точность проведения операции. В некоторых разработках предлагается динамически возбуждать иглу при введении в ткань [18]. Это приводит к снижению силы трения и упрощает процесс разрезания ткани при прокалывании. Пусть скорость поступательного движения инструмента в декартовых координатах равна 0,006 м/с вдоль оси ![]() инструмента
инструмента
![]()
Учитывая интервалы линейного разгона и торможения, для отрезка времени осуществления перехода равного 10 с, график скорости движения инструмента изображен на рисунке 7а. На рисунке 7б изображены соответствующие скорости сочленений при прохождении от точки к точке заданной траектории.
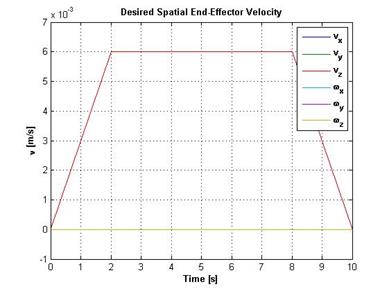

а) б)
Рисунок 7 – а) Скорость инструмента в абсолютной системе координат; б) скорость сочленений Робота-манипулятора в пространстве присоединенных координат
По аналогии с задачей кинематики здесь необходимо связать скорость движения инструмента в абсолютном пространстве со скоростями сочленений в пространстве присоединенных координат. В робототехнике эта связь устанавливается через матрицу Якоби преобразования ![]() в общем случае, размерностью
в общем случае, размерностью ![]() [4, 5, 16, 17]
[4, 5, 16, 17]
![]()
Для вычисления скоростей сочленений необходимо найти матрицу обратную матрице Якоби, что в нашем случае требует применения подхода Мура-Пенроуза (Moore-Penrose) [16], поскольку Робот-Манипулятор имеет избыточное число степеней подвижности ![]()
В общем случае ранг матрицы Якоби равен ![]() . Однако поскольку элементы матрицы
. Однако поскольку элементы матрицы ![]() являются функциями положения
являются функциями положения ![]() , некоторые конфигурации звеньев манипулятора приводят к снижению ранга матрицы. Такие конфигурации манипулятора называются сингулярными или вырожденными и соответствуют случаю, когда определитель матрицы Якоби равен нулю [5]
, некоторые конфигурации звеньев манипулятора приводят к снижению ранга матрицы. Такие конфигурации манипулятора называются сингулярными или вырожденными и соответствуют случаю, когда определитель матрицы Якоби равен нулю [5]
![]()
Эта проблема связана с использованием Эйлеровых углов. В иностранной литературе такое явление называется «GimbalLock» или «Шарнирный замок». Из-за того, что конечный результат серии вращений зависит от порядка промежуточных вращений, иногда случается, что вращение вокруг одной оси отображается на вращение вокруг другой оси. Иногда может быть невозможным вращать объект вокруг желаемой оси. Эта конфигурация называется «Шарнирный замок» [5].
Предположим, что объект последовательно вращают вокруг осей ![]() (на небольшой угол),
(на небольшой угол), ![]() ,
, ![]() и угол вращения вокруг оси
и угол вращения вокруг оси ![]() равен 90°. В этом случае вращение вокруг оси
равен 90°. В этом случае вращение вокруг оси ![]() происходит первым, что корректно. Вращение вокруг оси
происходит первым, что корректно. Вращение вокруг оси ![]() тоже совершается корректно. Однако после вращения вокруг оси
тоже совершается корректно. Однако после вращения вокруг оси ![]() на 90°, ось
на 90°, ось ![]() отображается на ось
отображается на ось ![]() . Таким образом, совершая вращение вокруг (относительной) оси
. Таким образом, совершая вращение вокруг (относительной) оси ![]() , фактически, совершается вращение объекта вокруг (абсолютной) оси
, фактически, совершается вращение объекта вокруг (абсолютной) оси ![]() [20].
[20].
Оценить наличие сингулярных точек позволяет расчет показателя манипулятивности. MATLAB® RoboticsToolboxиспользует метод Yoshikawa, вычисляющий показатель манипулятивности пропорционально объему эллипсоида
![]()
Если данный эллипсоид близок к сфере, то его радиусы являются величинами одного порядка и, следовательно, можно добиться произвольной допустимой скорости движения инструмента. Однако если один из радиусов очень мал и эллипсоид напоминает пластину, как показано на рисунке 8а, это означает, что инструмент не может достичь скорости в направлении этого малого радиуса. В данном случае это ось ![]() . Это распространенный, устоявшийся в робототехнике подход [5, 16].
. Это распространенный, устоявшийся в робототехнике подход [5, 16].
Исследуем возможности Робота-Манипулятора развивать скорость в каждой точке заданной траектории. Для этого вычислим показатель манипулятивности и изобразим эллипсоид скоростей. На рисунке 8б представлен эллипсоид линейной скорости для конфигурации манипулятора в первой узловой точке траектории, то есть для вектора присоединенных координат ![]()


а) б)
Рисунок 8 – а) Критический случай: эллипсоид вращения вблизи сингулярной точки; б) эллипсоид линейной скорости конфигурации Робота-Манипулятора в первой узловой точке траектории
Показатель манипулятивности равен 0,08886. Инструмент может достигать большей скорости в направлении оси ![]() , чем в направлении осей
, чем в направлении осей ![]() и
и ![]() . На рисунке 9 изображены эллипсоиды линейной скорости в положениях манипулятора, соответствующих другим узловым точкам траектории.
. На рисунке 9 изображены эллипсоиды линейной скорости в положениях манипулятора, соответствующих другим узловым точкам траектории.

Рисунок 9 – Эллипсоиды линейной скорости других конфигураций Робота-Манипулятора
По размеру эллипсоиды похожи друг на друга, так как имеют практически одинаковое значение показателя манипулятивности. Однако изображение эллипсоидов важно, поскольку именно величины радиусов указывают направление, в котором манипулятор не может достигать скорости. Критических ситуаций не наблюдается, что говорит об отсутствии сингулярностей при прохождении запланированной траектории. На рисунке 10 изображен эллипсоид угловой скорости Робота-Манипулятора для первой конфигурации.
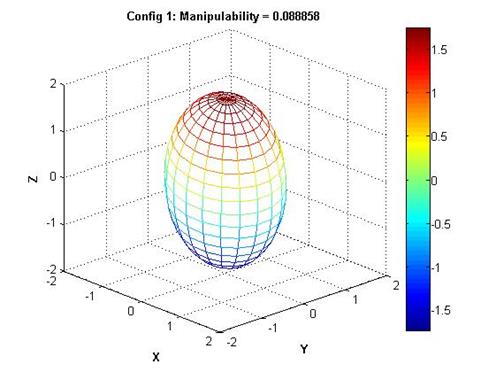
Рисунок 10 – Эллипсоид угловой скорости конфигурации Робота-Манипулятора в первой узловой точке траектории
Поступательная и вращательная скорости имеют разные размерности. Поэтому соответствующие эллипсоиды изображены отдельно. Однако манипулятивность комбинирует в себе информацию о линейной и вращательной скоростях инструмента манипулятора, поэтому ее величина в обоих случаях одна и та же. Эллипсоиды угловых скоростей других конфигураций Робота-Манипулятора приведены на рисунке 11.

Рисунок 11 – Эллипсоиды угловой скорости других конфигураций Робота-Манипулятора
Инструмент может достигать большей скорости в направлении оси ![]() , чем в направлении осей
, чем в направлении осей ![]() и
и ![]() . Однако критических случаев не наблюдается.
. Однако критических случаев не наблюдается.
2.4 Динамика Робота-Манипулятора
Аналогично задачам кинематики, существует две задачи динамики: прямая и обратная [4, 5, 16].
Прямая задача динамики: по заданным моментам ![]() в сочленениях определить обобщенные ускорения,
в сочленениях определить обобщенные ускорения,
![]()
интегрирование которых позволит получить значения обобщенных скоростей и координат сочленений
![]()
Обратная задача динамики: по заданным обобщенным координатам, скоростям и ускорениям определить действующие в сочленениях манипулятора моменты
![]()
Уравнение движения, полученное одним из двух методов: Лагранжа-Эйлера или Ньютона-Эйлера имеет вид
![]()
или для случая отсутствия внешних сил, действующих на инструмент
![]()
где ![]() - векторы обобщенных положений, скоростей и ускорений сочленений соответственно;
- векторы обобщенных положений, скоростей и ускорений сочленений соответственно; ![]() - матрица инерции;
- матрица инерции; ![]() - матрица кориолисовых и центробежных сил;
- матрица кориолисовых и центробежных сил; ![]() - трение;
- трение; ![]() - гравитационная нагрузка;
- гравитационная нагрузка; ![]() - Якобиан манипулятора;
- Якобиан манипулятора; ![]() - вектор нагрузок, приложенных к концу инструмента;
- вектор нагрузок, приложенных к концу инструмента; ![]() - вектор обобщенных сил [16].
- вектор обобщенных сил [16].
Проведем анализ динамических свойств Робота-Манипулятора. На рисунке 12 представлено изменение моментов во втором и третьем сочленении Робота-Манипулятора от гравитационной нагрузки при изменении обобщенных координат ![]() и
и ![]() от
от ![]() до
до ![]() . Полностью вертикальное положение Робота-Манипулятора, изображенное на рисунке 1а, соответствует нулевому значению обобщенных координат
. Полностью вертикальное положение Робота-Манипулятора, изображенное на рисунке 1а, соответствует нулевому значению обобщенных координат ![]() .
.
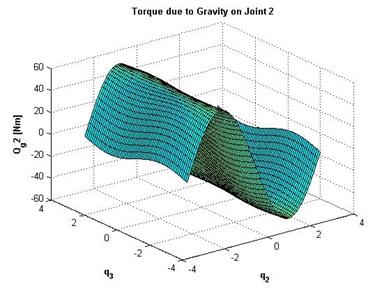

Рисунок 12 – Влияние гравитационной нагрузки на моменты: во втором сочленении (слева), в третьем сочленении (справа)
Из рисунка видно, что значение момента во втором сочленении меняется в интервале ![]() Нм, а в третьем сочленении - в интервале
Нм, а в третьем сочленении - в интервале ![]() Нм. Такой тип анализа важен для правильного подбора двигателей. Результаты аналогичных вычислений для 4-го, 5-го и 6-го, 7-го сочленений приведены на рисунках 13 - 14.
Нм. Такой тип анализа важен для правильного подбора двигателей. Результаты аналогичных вычислений для 4-го, 5-го и 6-го, 7-го сочленений приведены на рисунках 13 - 14.


Рисунок 13 – Влияние гравитационной нагрузки на моменты: в четвертом сочленении (слева), в пятом сочленении (справа)

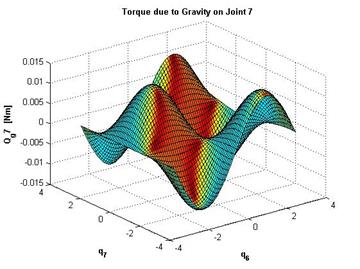
Рисунок 14 – Влияние гравитационной нагрузки на моменты: в шестом сочленении (слева), в седьмом сочленении (справа)
Для 7-го сочленения момент имеет маленькое значение, что корректно, поскольку седьмым звеном является инструмент – биопсийная игла. Моменты в сочленениях в зависимости от конфигурации ![]() Робота-Манипулятора приведены на рисунке 15.
Робота-Манипулятора приведены на рисунке 15.

Рисунок 15 – Моменты в сочленениях в зависимости от конфигурации Робота-Манипулятора
Так как траектория прямолинейная, то значительных изменений крутящих моментов не наблюдается за исключением второго сочленения. Связанное с ним звено совершает больше манипуляций, чем другие звенья.
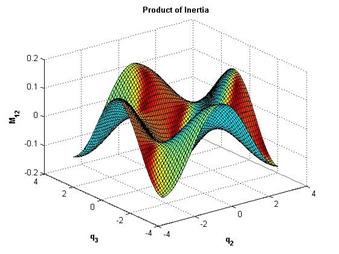
Матрица инерции ![]() также является функцией положения манипулятора. На рисунке 16а изображено значение инерции первого сочленения как функции присоединенных переменных сочленений 2 и 3 -
также является функцией положения манипулятора. На рисунке 16а изображено значение инерции первого сочленения как функции присоединенных переменных сочленений 2 и 3 - ![]() , на рисунке 16б -
, на рисунке 16б - ![]() .
.

Рису
Рисунок 16 – а) Значение инерции первого сочленения как функции присоединенных переменных сочленений 2 и 3 - ![]() б)
б) ![]()
2.5 Управление Роботом-Манипулятором
Если движение манипулятора описывается уравнениями Лагранжа-Эйлера или Ньютона-Эйлера, задачей управления является нахождение управляющих моментов [4]. В иностранной литературе этот метод называется ComputedTorqueControl/ InverseDynamicControl – метод вычисления управляющих моментов [5, 16, 17]. На рисунке 17 приведена схема модели управления в MATLAB® Simulink.
Обзор литературы показывает, что в большинстве случаев коэффициенты усиления выбирают постоянными, причем процесс подбора не является трудоемким [5, 10, 11, 16]. Подавая на вход требуемые положения ![]() , скорости
, скорости ![]() и ускорения
и ускорения ![]() сочленений и подбирая коэффициенты усиления, минимизируем ошибку по положению и по скорости. Перемещаясь вдоль траектории необходимо обеспечить точность позиционирования инструмента не более 0,05 мм в каждой узловой точке.
сочленений и подбирая коэффициенты усиления, минимизируем ошибку по положению и по скорости. Перемещаясь вдоль траектории необходимо обеспечить точность позиционирования инструмента не более 0,05 мм в каждой узловой точке.
Отладка схемы управления позволила определить подходящие параметры системы, обеспечивающие необходимую точность. Приняв время интегрирования ![]() с, количество шагов по времени при перемещении от точки к точке траектории
с, количество шагов по времени при перемещении от точки к точке траектории![]() коэффициент усиления обратной связи по положению
коэффициент усиления обратной связи по положению ![]() а по скорости
а по скорости ![]() получаем следующие результаты. Ошибка по положению и по скорости каждого сочленения изображена на рисунке 18а,б.
получаем следующие результаты. Ошибка по положению и по скорости каждого сочленения изображена на рисунке 18а,б.
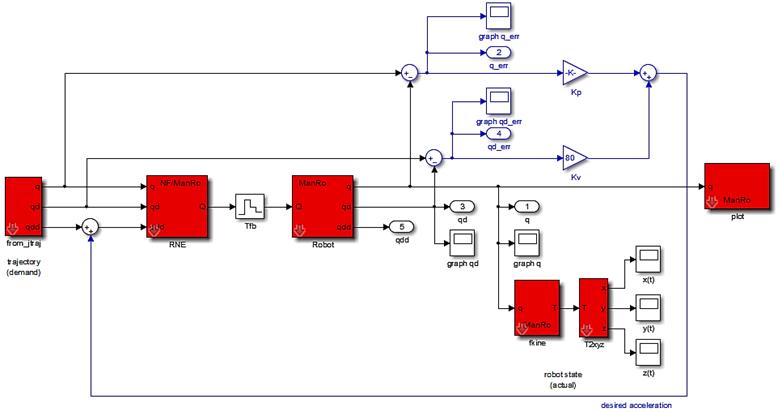
Рисунок 17 – Схема модели управления в MATLAB® Simulink
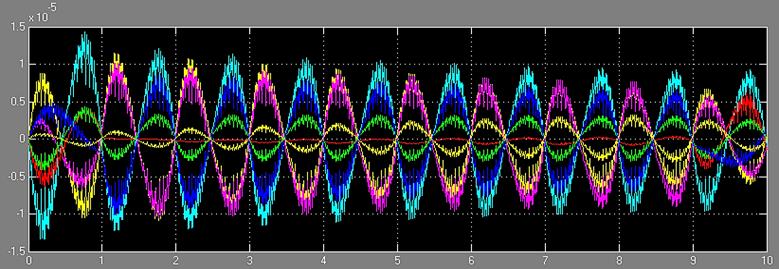
а)
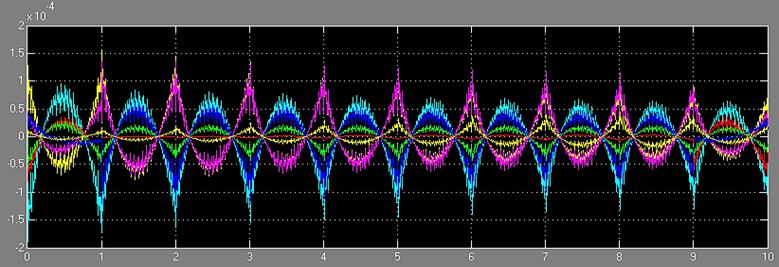
б)
Рисунок 18 – а) Ошибка по положению; б) ошибка по скорости
Видно, что в первом случае порядок ошибки равен ![]() а во втором -
а во втором - ![]() что, на самом деле является хорошим результатом. Требуемые и полученные координаты сочленений представлены на рисунке 19а,б.
что, на самом деле является хорошим результатом. Требуемые и полученные координаты сочленений представлены на рисунке 19а,б.

а)
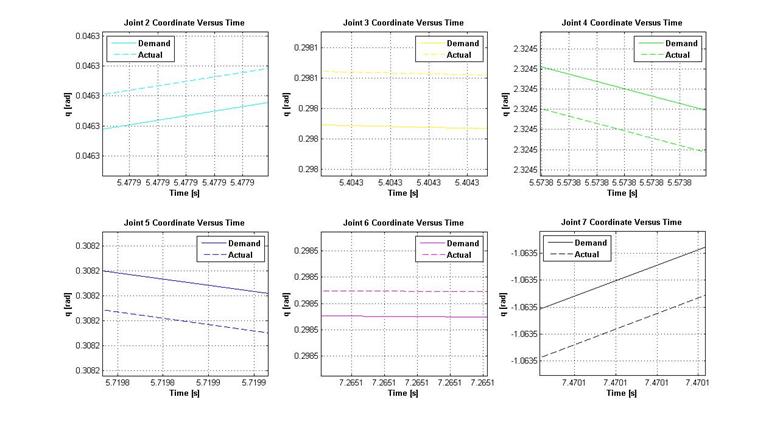
б)
Рисунок 19 – Требуемые и полученные координаты сочленений
Требуемая и полученная траектории движения инструмента в пространстве представлены на рисунке 20, а на рисунке 21 - в проекциях на плоскости ![]() и
и ![]() .
.
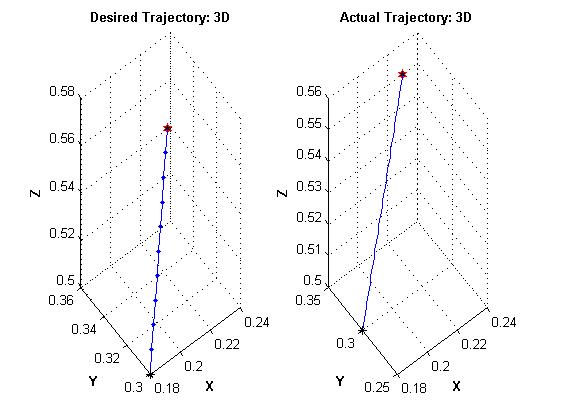
Рисунок 20 – Требуемая (слева) и полученная (справа) траектории движения инструмента в пространстве
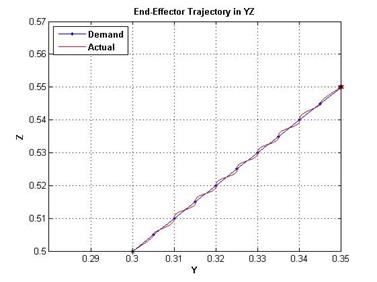
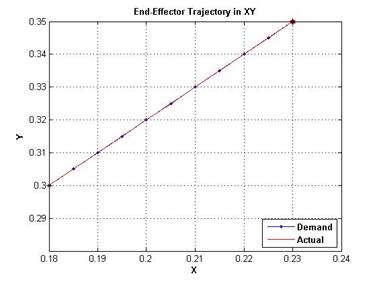
а) б)
Рисунок 21 – Требуемая и полученная траектории движения проекциях на плоскости ![]() (слева) и
(слева) и ![]() (справа)
(справа)
Из графиков видно, что движение конца инструмента между узловыми точками осуществляется по окружности. Это связано с тем, что при перемещении инструмента между узловыми точками за определенное количество шагов по времени, известны координаты только этих узловых точек. Поскольку во время движения Робот-Манипулятор вращается вокруг своего первого звена – «талии», то естественно при совместном движении инструмент будет двигаться по дуге окружности [5]. Точность позиционирования инструмента в узловых точках приведена на рисунке 22 и ее максимальное по модулю значение составляет ![]() м или
м или ![]() мм.
мм.

Рисунок 22 – Точность позиционирования инструмента в узловых точках траектории
Проекция заданной и полученной траекторий движения на плоскость ![]() показана на рисунке 23.Точность позиционирования в интервалах между заданными узловыми точками траектории составляет порядка
показана на рисунке 23.Точность позиционирования в интервалах между заданными узловыми точками траектории составляет порядка ![]() мм.
мм.

Рисунок 23 – Точность позиционирования в интервалах между заданными узловыми точками траектории
На рисунке 24 представлены составляющие вектора скорости движения инструмента в абсолютной системе координат в заданных узловых точках (слева) и на протяжении всей траектории движения (справа). Видно, что график 24 (слева) полностью соответствует рисунку 7а. Максимальное значение ошибки по скорости в узловых точках составляет ![]() , а в интервалах между точками - порядка
, а в интервалах между точками - порядка ![]()
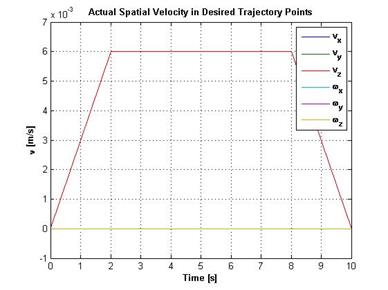
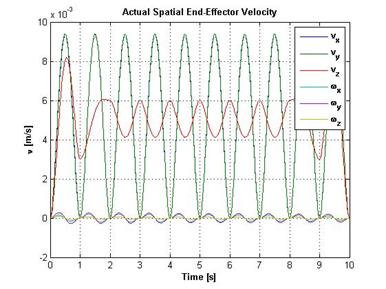
Рисунок 24 – Составляющие вектора скорости движения инструмента в абсолютной системе координат в заданных узловых точках (слева) и на протяжении всей траектории движения (справа)
3 Анализ результатов и общие выводы
Изучение проблемы позиционирования инструмента хирургического Робота-Манипулятора позволяет сделать следующие выводы. Наличие семи степеней подвижности увеличивает маневренность Робота-Манипулятора, а, следовательно, возможности его использования. Выбранная система управления и подобранные параметры позволили с точностью ![]() мм позиционировать инструмент в заданных точках траектории. Значение ошибки по скорости в этих точках составляет
мм позиционировать инструмент в заданных точках траектории. Значение ошибки по скорости в этих точках составляет ![]() что, практически можно считать равной нулю. Величина ошибки позиционирования инструмента в интервалах между узловыми точками траектории составляет
что, практически можно считать равной нулю. Величина ошибки позиционирования инструмента в интервалах между узловыми точками траектории составляет ![]() мм, что меньше, чем требуется техническим заданием (1 мм) [1], однако, больше, чем ожидается от нейрохирургических роботов-ассистентов [15]. Поскольку выбранное количество узловых точек траектории мало и выбрано лишь для удобства расчетов, данное значение нельзя считать показательным. Скорость в интервалах между узловыми точками на данном этапе не является особенно важным критерием, за исключением нулевой скорости в точки цели.
мм, что меньше, чем требуется техническим заданием (1 мм) [1], однако, больше, чем ожидается от нейрохирургических роботов-ассистентов [15]. Поскольку выбранное количество узловых точек траектории мало и выбрано лишь для удобства расчетов, данное значение нельзя считать показательным. Скорость в интервалах между узловыми точками на данном этапе не является особенно важным критерием, за исключением нулевой скорости в точки цели.
Заключение
Полученные результаты говорят о том, что разрабатываемая модель Робота-Манипулятора позволяет выполнять нейрохирургические процедуры, поскольку имеет высокие показатели точности позиционирования инструмента в заданных точках траектории. На практике нейронавигационные станции обеспечивают высокую дискретизацию запланированной траектории, что сокращает расстояние между точками, и, тем самым повышает точность движения инструмента в интервалах между узловыми точками.
Благодарность
Работа выполнена при поддержке Министерства образования и науки РФ в рамках федеральной целевой научно-технической программы «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России» на 2007 – 2012 годы, номер контракта 16.523.11.3011.
Список литературы
1.Робот-Манипулятор: отчет о НИР/ ЗАО «ЭКОИНВЕНТ»; рук. О.С. Нарайкин. М., 2012. 211 с. № ГР 01201251073. Инв. № ЭИ20120518.
2.Ситников А.Р. Биопсия. Режим доступа: http://www.dr-sitnikov.ru/sitnikov58/ (дата обращения 08.05.2013).
3.Богданова Ю.В., Гуськов А.М., Жидких И.В., Нарайкин О.С., Шурхай В.А. Проблемы разработки стереотаксических систем наведения хирургического инструмента на примере биопсии головного мозга // Наука и Образование: электронное научно-техническое издание. 2012. № 12. DOI: 10.7463/0113.0486770
4.Fu K.S. Gonzalez R.C., Lee C.S.G. Robotics: Control, Sensing, Vision and Intelligence. McGraw-Hill Book Company, 1987. 580 p.
5.Corke P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB. Springer, 2011. 558 c.DOI: 10.1007/978-3-642-20144-8
6.Piltan F., Emamzadeh S., Hivand Z., Shahriyari F., Mirzaei M. PUMA-560 Robot Manipulator Position Computed Torque Control Methods Using MATLAB/SIMULINK and Their Integration into Graduate Nonlinear Control and MATLAB Courses // International Journal of Robotics and Automation (IJRA). 2012. Vol. 3, iss. 3. P. 167-191.
7.Khosla K. Choosing Sampling Rates for Robot Control. Pittsburgh: Carnegie Mellon University, 1987. 22 p.
8.Jin N.M. Neuro Feedback Linearization in the Control of Robotic Manipulators: Degree of Master. National University of Singapure, 2004. 98 p.
9.Gupta M.K., Singh A.K., Bansal K. Trajectory Tracking Control of Robot Manipulators // International Journal of Computer Applications. 2013. Vol. 64, no. 10. P. 28-32.
10. Craig J.J. Introdiction to Robotics, Mechanics and Control. 3rd ed. Pearson Education International, 2005. 408 p.
11. Kang H. Robotic Assisted Suturing in Minimally Invasive Surgery: Degree of PhD. New York, Rensselaer Polytechnic Institute, 2002. 183 p.
12. Ata A.A., Myo T.R. Optimal Point-to-Point Trajectory Tracking of Redundant Manipulators using Generalized Pattern Search // International Journal of Advanced Robotic Systems. 2005. Vol. 2, no. 3. P. 239-244.
13. Банин Е.П., Барышева О.П., Батанов А.Ф., Богданова Ю.В., Гуськов А.М., Козубняк С.А., Нарайкин О.С., Пуценко А.А. Координатная связь медицинского робота - манипулятора // Наука и Образование: электронное научно-техническое издание. 2012. № 12.DOI: 10.7463/0113.0520630
- Casadei C., Fiorini P., Martelli S., Montanari M. Improving the Performance of PC-Based Controllers for Robot-Assisted Surgery. California Institute of Technology, Jet Propulsion Laboratory. Available at: http://trs-new.jpl.nasa.gov/dspace/bitstream/2014/19372/1/98-0715.pdf , accessed 08.05.2013.
15. ООО «Евраз Медикал Групп». ROSA. Режим доступа: http://evrazmed.ru/catalog/robot-assistent/ (дата обращения 08.05.2013).
16. Melchiorri C. Kinematic Model of Robot Manipulators. Presentation. Universit`a di Bologna. Available at: http://www-lar.deis.unibo.it/people/cmelchiorri/Files_Robotica/FIR_04_Kinem.pdf , accessed 08.05.2013.
17. Heverly M., Dupont P., Triedman J. Trajectory optimization for dynamic needle insertion // Proc. of IEEE International Conference on Robotics and Automation (ICRA) (Barcelona, April 2005). 2005. P. 1646-1651.
18. Allen G., Brailsford B., Hulton A., Hunt W., Ober W., Muftu S. Dynamically Oscillated Biopsy Needle. Available at: http://www.mie.neu.edu/pdfs/Capstone/Mechanical_Engineering/ME%202011%2004%20Dynamically%20Oscillating%20Biopsy%20Needle.pdf , accessed 08.05.2013.
19. Siciliano B., Khatib O. (Eds). Springer Handbook of Robotics. Springer Berlin Heidelberg, 2008. 1628 p. DOI: 10.1007/978-3-540-30301-5
20. Матрицы и квартенионы. Режим доступа: http://www.rossprogrammproduct.com/translations/Matrix%20and%20Quaternion%20FAQ.htm#Q31(дата обращения 20.02.2013).
Публикации с ключевыми словами: позиционирование инструмента, хирургический Робот-Манипулятор, движение по траектории, метод вычисления управляющих моментов, MATLAB® Robotics Toolbox, Simulink®, биопсия мозга
Публикации со словами: позиционирование инструмента, хирургический Робот-Манипулятор, движение по траектории, метод вычисления управляющих моментов, MATLAB® Robotics Toolbox, Simulink®, биопсия мозга
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



