научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2013
DOI: 10.7463/0613.0567697
УДК 62-522.2
Россия, МГТУ им. Н.Э. Баумана
ОАО «КАМАЗ»
Введение
Особенности эксплуатации многоосных колесных машин (МКМ) предъявляют высокие требования к их эксплуатационным показателям. Одним из важнейших показателей является подвижность, т.е. способность МКМ двигаться по дорогам с заданными статистическими характеристиками неровностей с заданными скоростями и преодолевать единичные препятствия (эскарп, контрэскарп, траншея и др.).
В настоящее время большое количество факторов ограничивает мобильность МКМ. Тягово-скоростные свойства автомобиля оказывают основное влияние на формирование максимальных и средних скоростей движения. Однако, и другие эксплуатационные качества, влияющие на показатели устойчивости, управляемости, проходимости, вибронагруженности, также в большой степени оказывают влияние на скорость движения машины. Совершенствование конструкций подвесок, создание управляемых систем подрессоривания в подавляющем большинстве случаев позволяет улучшить эксплуатационные показатели, что способствует увеличению средних и максимальных скоростей движения [1].
Изучению вопросов, связанных с обеспечением плавности хода МКМ, в том числе и с помощью разработки управляемых систем подрессоривания, посвящено большое число исследований советских, российских и зарубежных ученых и инженеров. Тем не менее, несмотря на достигнутые успехи, системы первичного подрессоривания по-прежнему сдерживают дальнейший рост параметров быстроходности.
Главная причина этого заключается в том, что широкий спектр эксплуатационных режимов МКМ предъявляет противоречивые требования к системе первичного подрессоривания. Во-первых, при движении по дорогам хорошего качества с высокими скоростями приоритетным является требование обеспечения устойчивости и управляемости машины. Однако, здесь положение усугубляется склонностью МКМ к опрокидыванию ввиду больших значений отношения базы машины к ширине колеи при высоко расположенном центре тяжести. Для обеспечения этих требований подвеска должна быть «жесткой» и короткоходной.
В случае движения по грунтовым дорогам на первое место выходят требования по снижению вибронагруженности экипажа и повышению плавности хода. Здесь, наоборот, требуется «мягкая» длинноходная подвеска.
В момент преодоления машиной крупных единичных препятствий (эскарпы, траншеи, косогоры и др.) силы, действующие на несущую систему МКМ со стороны подвески, в несколько раз превышают статическую нагрузку [2]. Это заставляет разработчиков вводить ограничения, связанные с уменьшением уровня демпфирования и коэффициента динамичности подвески, которая должна быть «мягкой» и длинноходной.
И, наконец, кроме кинематического воздействия со стороны неровностей дороги, на корпус МКМ действуют силы, возникающие при разгоне, торможении, повороте, действии импульсной боковой нагрузки. Здесь, в первую очередь, требуется обеспечение динамической стабилизации корпуса, т.е. устойчивости, для чего подвеска должна быть «жесткой».
Одним из перспективных способов решения указанных проблем является разработка управляемых систем подрессоривания, обеспечивающих стабилизацию корпуса МКМ при различных воздействиях. В работах [3, 4] был предложен закон динамической стабилизации на базе четкого ПД-регулятора с адаптивной настройкой параметров в зависимости от «жесткости» входного воздействия. Однако известно, что четкие ПИД-регуляторы имеют недостаточную эффективность при управлении нелинейными системами, а также при недостаточной информации об объекте управления [5].
1. Применение нечёткой логики для подстройки коэффициентов регулятора
В последнее время широкую популярность находят нечеткие модели и алгоритмы управления [6-8]. Известно, что нечеткое управление основано на использовании не столько аналитических или теоретических моделей, сколько на практическом применении знаний квалифицированных специалистов, представленных в форме лингвистических баз правил. Нечеткое управление эффективно в случаях недетерминированности параметров объектов, когда существует определенный опыт экспертов по управлению и настройке автоматизированной системы регулирования (АСР). Теория нечеткой логики позволяет использовать знания специалистов — экспертов с целью улучшения процессов управления и оказания помощи по настройке типовых регуляторов. Исходя из вышесказанного, задача создания метода адаптации ПД-регулятора, реализующего опыт экспертов, становится актуальной.
Нечёткая логика в ПД-регуляторах используется преимущественно двумя путями: для построения самого регулятора и для организации подстройки коэффициентов ПД-регулятора. Подстройка коэффициентов регулятора может быть выполнена на основании эвристических правил автоматически, с помощью блока нечёткой логики, который использует базу правил и методы нечёткого вывода. Фаззи-подстройка позволяет уменьшить перерегулирование, снизить время установления и повысить робастность ПИД-регулятора [9].
Рассмотрим подробно процесс настройки пропорционально-дифференциального регулятора, обеспечивающего стабилизацию корпуса многоосной колесной машины по трем координатам: углам крена и тангажа и вертикальному положению центра масс. В работе [1] показано, что стабилизация возможна по каждой из координат в отдельности на основании уравнения регулятора, которое в общем виде можно записать как
![]()
где U – управляющее силовое воздействие на корпус;
х – значение фазовой координаты;
К, Кр – коэффициенты регулятора.
Процесс автонастройки регулятора с помощью блока нечёткой логики начинается с поиска начальных приближений коэффициентов регулятора К, Кр. Эта процедура описана в работе [3]. В процессе настройки регулятора используется несколько шагов [10].
Сначала выбираются диапазоны входных и выходных сигналов, форма функций принадлежности искомых параметров, правила нечёткого вывода, механизм логического вывода, метод дефаззификации и диапазоны масштабных множителей, необходимых для пересчёта чётких переменных в нечёткие.
1.1. Процедура фаззификации
Начнем процедуру фаззификации. Введем следующие входные лингвистические переменные Х1 – Х6:
1) Х1: абсолютное значение угла продольного наклона корпуса;
2) Х2: абсолютное значение продольно-угловой скорости наклона корпуса;
3) Х3: абсолютное значение угла поперечного наклона корпуса;
4) Х4: абсолютное значение поперечно-угловой скорости наклона корпуса;
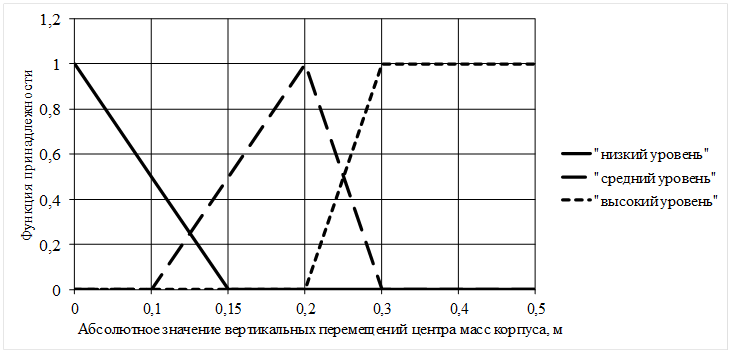
5) Х5: абсолютное значение вертикального перемещения центра масс корпуса;
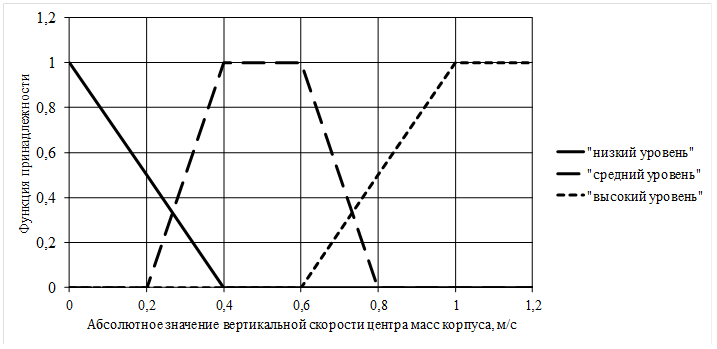
6) Х6: абсолютное значение скорости вертикального перемещения центра масс корпуса.
Введем также две выходные переменные Y1 и Y2:
1) Y1: коэффициент К;
2) Y2: коэффициент Кр.
В нечеткой логике значения любой величины представляются не числами, а словами естественного языка и называются термами. Введем следующие термы для всех лингвистических переменных: «высокий уровень»; «средний уровень»; «низкий уровень».
Для завершения процедуры фаззификации построим функцию принадлежности для каждой лингвистической переменной на основе экспертной информации. Формулировка задачи построения функций принадлежности приведена в работе [11].
Обработка результатов экспертного опроса проводится на основе статистических методов с целью определения достоверности и согласованности их оценок. Если в результате проведения такого анализа будет установлено, что мнения экспертов имеют слишком большой разброс, необходимо провести коррекцию их позиции и повторить опрос. Методика обработки мнения экспертов приведена в [12].
1.2. Определение значений функций принадлежности для входных и выходных лингвистических переменных
На основе обработки мнений пяти экспертов по известным методикам [11, 12] построены функции принадлежности входных (рис. 1-5) и выходных (рис. 6) переменных.
|
Рис. 1. Функции принадлежности входной переменной Х1 |
|
Рис. 2. Функции принадлежности входной переменной Х2
|
|
Рис. 3. Функции принадлежности входной переменной Х3 |
|
Рис. 4. Функции принадлежности входной переменной Х5
|
|
Рис. 5. Функции принадлежности входной переменной Х6 |
|
Рис. 6. Функции принадлежности выходных переменных Y1 и Y2 |
1.3. Правила и механизм нечёткого логического вывода
Следующий этап – разработка нечетких правил. Большинство нечетких систем используют продукционные правила, связывающие лингвистические переменные [13].
Совокупность таких правил описывает стратегию принятия решения, применяемую в данной задаче.
Типичное продукционное правило состоит из антецедента (часть ЕСЛИ…) и консеквента (часто ТО…). Антецедент может содержать более одной посылки. В этом случае они объединяются посредством логических связок И или ИЛИ. Будем использовать при построении правил только связку И.
Процесс вычисления нечеткого правила называется нечетким логическим выводом и подразделяется на два этапа: обобщение и заключение. Будем использовать алгоритм нечеткого логического вывода Мамдани [11]. Пример нечеткого правила выглядит следующим образом:
ЕСЛИ Х1 «Абсолютное значение угла продольного наклона корпуса» = «средний уровень» И Х2 «Абсолютное значение продольно-угловой скорости корпуса» = «средний уровень», ТО Y1 «коэффициент К» = «средний уровень».
Полный набор нечетких правил приведен в таблицах 1 - 3.
Таблица 1.
Таблица нечетких правил для выходной переменной Y1 «коэффициент К»
|
| |||
Низкий уровень | Средний уровень | Высокий уровень | ||
| Низкий уровень | Низкий уровень | Низкий уровень | Низкий уровень |
Средний уровень | Средний уровень | Средний уровень | Средний уровень | |
Высокий уровень | Высокий уровень | Высокий уровень | Высокий уровень | |
Примечание: ![]() - входные переменные Х2 или Х4 или Х6;
- входные переменные Х2 или Х4 или Х6; ![]() - входные переменные Х1 или Х3 или Х5 соответственно.
- входные переменные Х1 или Х3 или Х5 соответственно.
Таблица 2.
Таблица нечетких правил для выходной переменной Y2
«коэффициент Кр» для случая ![]()
|
| |||
Низкий уровень | Средний уровень | Высокий уровень | ||
| Низкий уровень | Высокий уровень | Высокий уровень | Высокий уровень |
Средний уровень | Высокий уровень | Средний уровень | Низкий | |
Высокий уровень | Низкий | Низкий | Низкий | |
Примечание: ![]() - входные переменные Х2 или Х4 или Х6;
- входные переменные Х2 или Х4 или Х6; ![]() - входные переменные Х1 или Х3 или Х5 соответственно.
- входные переменные Х1 или Х3 или Х5 соответственно.
Таблица 3.
Таблица нечетких правил для выходной переменной Y2
«коэффициент Кр» для случая ![]()
|
| |||
Низкий уровень | Средний уровень | Высокий уровень | ||
| Низкий уровень | Низкий уровень | Средний уровень | Высокий уровень |
Средний уровень | Низкий уровень | Средний уровень | Высокий уровень | |
Высокий уровень | Высокий уровень | Высокий уровень | Высокий уровень | |
Примечание: ![]() - входные переменные Х2 или Х4 или Х6;
- входные переменные Х2 или Х4 или Х6; ![]() - входные переменные Х1 или Х3 или Х5 соответственно.
- входные переменные Х1 или Х3 или Х5 соответственно.
В результате логического вывода по j-му правилу получаем нечеткое значение выходной переменной Yj
![]()
где ![]() - значение функций принадлежности по j-му правилу для входных переменных Х1 и Х2 соответственно. Такая операция взятия минимума называется импликацией [11].
- значение функций принадлежности по j-му правилу для входных переменных Х1 и Х2 соответственно. Такая операция взятия минимума называется импликацией [11].
Например, если для переменной «Абсолютное значение угла продольного наклона корпуса» ![]() , а для переменной «Абсолютное значение продольно-угловой скорости корпуса»
, а для переменной «Абсолютное значение продольно-угловой скорости корпуса» ![]() , то
, то ![]()
Операция импликации означает «срезание» функции принадлежности ![]() . Смысл этой операции пояснен в работе [11].
. Смысл этой операции пояснен в работе [11].
Если множество термов L является «размытым», то результатом нечеткого логического вывода может быть несколько термов ![]() выходной переменной. В этом случае наряду с операцией импликации для каждого значения
выходной переменной. В этом случае наряду с операцией импликации для каждого значения ![]() необходимо провести операцию агрегирования (объединения) нечеткого множества
необходимо провести операцию агрегирования (объединения) нечеткого множества ![]() , которая обычно реализуется операцией взятия максимума [11].
, которая обычно реализуется операцией взятия максимума [11].
1.4. Процедура дефаззификации
На последнем этапе необходимо осуществить переход от нечетких значений выходной величины Y значения прогноза определяющего параметра к четкому числовому значению. Эта операция называется дефаззификацией (устранением нечеткости). Наиболее часто применяется дефаззификация по методу центра тяжести [11]. При этом четкое значение определяется как проекция центра тяжести фигуры, ограниченной функциями принадлежности выходной переменной с допустимыми значениями, по формуле
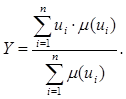
Рассмотренный метод нечеткого моделирования может быть отнесен к числу полуавтоматических процедур, поскольку большинство выполняемых шагов, включая построение универсума на основании множества исходных данных задачи, могут быть эффективно воплощены в программной форме, однако участие аналитиков (экспертов) при формировании соответствующих нечетких множеств играет также огромную роль.
2. Ограничения на управляющее воздействие
2.1. Для активной системы подрессоривания
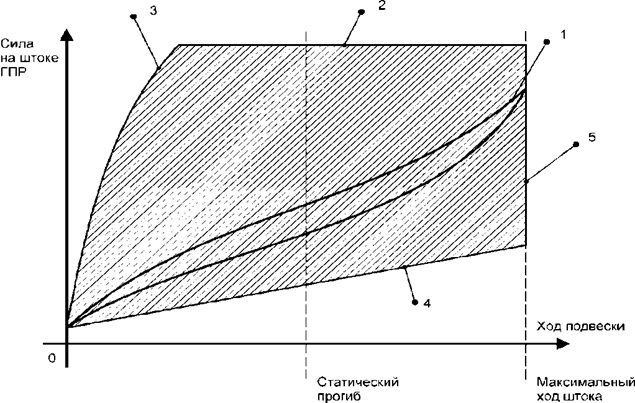
При разработке систем автоматического регулирования актуальной задачей является использование таких алгоритмов управления, которые использовали бы какую-либо функцию, ограничивающую выходной сигнал. Выходной сигнал регулятора должен иметь ограниченную амплитуду, по крайней мере, по двум причинам: во-первых, в связи с ограниченными энергетическими ресурсами (реализация больших величин управляющих сигналов требует больших энергетических затрат); во-вторых, рабочий диапазон давлений в пневмогидравлическом устройстве системы подрессоривания всегда ограничен, в случае превышения давлением предельно допустимой величины срабатывает предохранительный клапан. Таким образом, всегда определяется верхняя граница допустимых управляющих воздействий. Существует также нижняя граница управляющих воздействий, которая вместе с верхней границей образуют область допустимых значений управления. Рассмотрим такую область допустимых воздействий для пневмогидравлической рессоры (ПГР). На рис. 7 область допустимых значений управляющих воздействий заштрихована. В работе были приняты следующие значения ограничений: максимальная мощность, которая может быть затрачена на управление подвеской, равна 120 кВт; максимальное давление в гидросистеме – 30 МПа.
|
Рис. 7. Область допустимых значений управляющих воздействий для ПГР:
|
2.2. Для полуактивной системы подрессоривания
Рассмотрим управляемые полуактивные системы подрессоривания на основе магнитореологического демпфера (МРД). На рис. 8 область допустимых значений управляющих воздействий заштрихована.
3. Анализ эффективности разработанного адаптивного закона управления активной и полуактивной системами подрессоривания
Для оценки эффективности разработанного адаптивного непрерывного пропорционально-дифференциального закона управления полуактивной подвеской и того же закона для активной системы подрессоривания на различных скоростях движения по грунтовой дороге 2-й категории [1] моделировалось движение МКМ в диапазоне скоростей 10…60 км/ч. Математическая модель движения МКМ представлена в работе [14], технические характеристики машины – в работе [1].
|
Рис. 8. Область допустимых значений управляющих воздействий для МРД: |
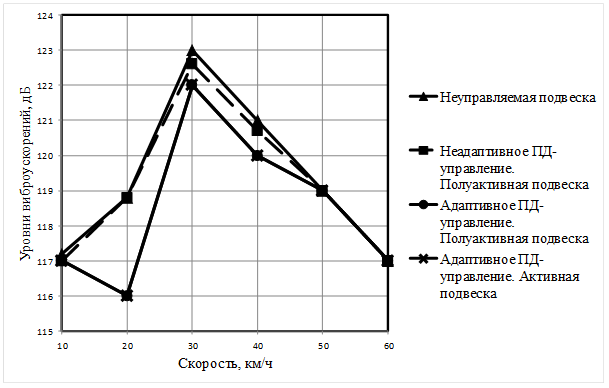
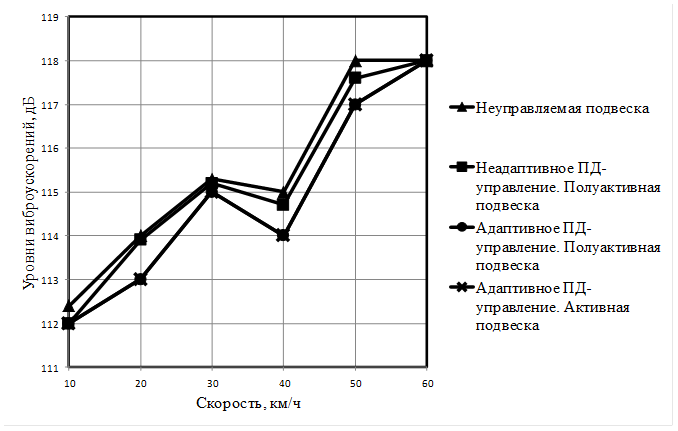
На рис. 9 (а – д) представлены уровни вертикальных виброускорений на месте водителя для I – V октавных полос частот для различных систем подрессоривания.
|
а) |
|
б) |
|
в) |
|
г) |
|
д) |
Рис. 9. Уровни вертикальных виброускорений в октавных полосах частот: |
Для проведения сравнительного анализа эффективности разработанного адаптивного непрерывного пропорционально-дифференциального закона управления полуактивной подвеской и того же закона для активной системы подрессоривания используем критерий Ki (для i-ой скорости движения на всей совокупности грунтовых дорог), характеризующий работу данной системы по сравнению с неуправляемой подвеской [1]:
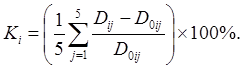 (1)
(1)
Здесь ![]() - дисперсия вертикальных ускорений на месте водителя для случая управляемой подвески при движении с i-ой скоростью; j – номер категории грунтовой дороги.
- дисперсия вертикальных ускорений на месте водителя для случая управляемой подвески при движении с i-ой скоростью; j – номер категории грунтовой дороги.
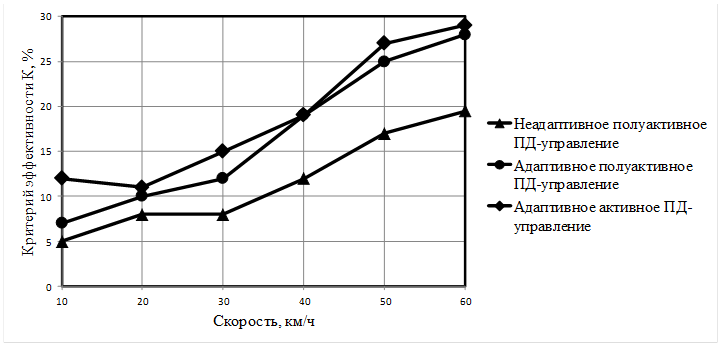
Критерий (1) характеризует степень снижения дисперсии вертикальных ускорений на месте водителя для случая управляемой подвески по сравнению с неуправляемой системой подрессоривания. На рис. 10 показана зависимость показателя эффективности Ki для различных законов управления от скорости движения для всей совокупности грунтовых дорог.
|
Рис. 10. Зависимость критерия эффективности Kiдля различных законов управления подвеской для различных скоростей движения по грунтовым дорогам |
Анализ представленных результатов позволяет сделать вывод о том, что эффективность (снижение уровня дисперсии вертикальных ускорений на месте водителя по сравнению с неуправляемой подвеской) адаптивного пропорционально-дифференциального закона для активной системы подрессоривания составляет 12…29%. Эффективность для того же закона для полуактивной системы подрессоривания составляет 7…28%.
4. Оценка энергетических затрат на управление активной подвеской при движении по случайному профилю
Оценка средней мощности N, затраченной на управление пневмогидравлической рессорой путем нагнетания или стравливания рабочей жидкости из полости над поршнем ПГР проводилась по формуле
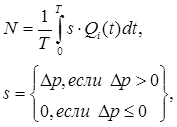
где Т – интервал времени;
Qi (t) - расход рабочей жидкости на управление i-ой ПГР;
Δр – требуемый перепад давлений.
Если приращение усилия в подвеске ΔPi > 0, то разность давлений в поршневой полости и напорной магистрали гидросистемы Δpi>0, и наоборот. Разность давлений Δpi рассчитывается по формуле
Δpi = ΔPi /S,
где S – площадь цилиндра ПГР.
Расход рабочей жидкости на управление Qi (t) определялся формулой

Значения средней мощности, затраченной на управление подвеской при движении по грунтовым дорогам 1…5 категорий в диапазоне скоростей 10 … 70 км/час приведены на рис. 11. Максимальное значение мощности, затрачиваемой на управление для активной системы подрессоривания достигает значения 115 кВт.
Для полуактивной подвески затраты энергии на управление сводятся к затратам на создание электромагнитного поля в локальной зоне дроссельных отверстий магнито-реологического демпфера, что на порядок меньше затрат на активное управление.
|
Рис. 11. Средняя мощность, затраченная на управление при движении по грунтовой дороге с различными скоростями |
Выводы
1) На основе применения методов нечеткой логики разработан адаптивный пропорционально-дифференциальный закон непрерывного управления системой подрессоривания многоосных колесных машин.
2) Установлено методами имитационного моделирования, что эффективность (снижение уровня дисперсии вертикальных ускорений на месте водителя по сравнению с неуправляемой подвеской) адаптивного пропорционально-дифференциального закона для активной системы подрессоривания составляет 12…29%. Эффективность для того же закона для полуактивной системы подрессоривания составляет 7…28%.
3) Установлено методами имитационного моделирования, что затраты энергии на управление активной системой подрессоривания для МКМ общей массой 60 т и колесной формулой 8х8 доходят до 115 кВт. Затраты энергии на управление полуактивной системой подрессоривания на порядок меньше по сравнению с активной подвеской.
4) При соизмеримой эффективности и существенно меньших энергетических затратах на управление адаптивный пропорционально-дифференциальный закон для полуактивной системы подрессоривания можно считать более предпочтительным для практического применения в подвесках МКМ по сравнению с аналогичным законом для активных систем подрессоривания.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках договора №9905/17/07-к-12 между ОАО «КАМАЗ» и «Московским государственным техническим университетом имени Н.Э. Баумана».
Список литературы
- Жилейкин М.М. Сравнительный анализ эффективности работы непрерывной и релейной систем управления подвеской многоосных колесных машин // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 3. Режим доступа: http://technomag.edu.ru/doc/347783.html (дата обращения 26.05.2013).
- Белоусов Б.Н., Попов С.Д. Колесные транспортные средства особо большой грузоподъемности. Конструкция. Теория. Расчет / Под общ. ред. Б.Н. Белоусова. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. 728 с.
- Жилейкин М.М. Синтез адаптивной динамической непрерывной системы гашения колебаний корпуса многоосных колесных машин // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 10. Режим доступа: http://technomag.edu.ru/doc/347169.html (дата обращения 26.05.2013).
- Жилейкин М.М. Синтез адаптивной динамической непрерывной системы стабилизации корпуса // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 11. Режим доступа: http://technomag.edu.ru/doc/347435.html (дата обращения 26.05.2013).
- Ротач В.Я., Клюев А.С. Автоматизация настройки систем управления. М.: Энергоиздат, 1984. 272 с.
- Леоненков А.Ю. Нечеткое моделирование в среде Matlab и fuzzyTech. СПб.: БХВ, 2003. 720 с.
- Мелихов А.Н., Берштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой. М.: Наука, 1990. 272 с.
- Алиев Р.А., Церковный А.Э., Мамедова Г.А. Управление производством при нечеткой исходной информации. М.: Энергоиздат. 1991. 234 с.
- Yesil E., Guzelkaya M., Eksin I. Internal model control based fuzzygain scheduling technique of PID controllers // World Automation Congress (28 June - 1 July 2004): Proceedings. 2004. Vol. 17. P. 501-506.
- Feng H.M. A selftuning fuzzy control system design // IFSA World-Congress and 20th NAFIPS International Conference (25-28 July 2001). 2001. Vol. 1. P. 209-214.
- Штовба С.Д. Проектирование нечетких систем средствами MATLAB. М.: Горячая линия – Телеком, 2007. 288 с.
- Плиев И.А. Автомобили многоцелевого назначения. Формирование технического облика АМН в составе семейств: монография. М.: МГИУ, 2011. 262 с.
- Гриняев С.В. Нечеткая логика в системах управления // Компьютерра Online: электронный ресурс. Режим доступа: http://www.computerra.ru/offline/2001/415/13052/ (дата обращения 26.05.2013).
- Проектирование полноприводных колесных машин: учебник для вузов. В 3 т. Т. 3 / Афанасьев Б. А., Белоусов Б. Н., Жеглов Л. Ф. [и др.]; Под ред. А.А. Полунгяна. М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. 432 с.
Публикации с ключевыми словами: нечеткая логика, адаптивное управление, многоосные колесные машины, управляемые системы подрессоривания
Публикации со словами: нечеткая логика, адаптивное управление, многоосные колесные машины, управляемые системы подрессоривания
Смотри также:
- Разработка непрерывного закона управления полуактивной системой подрессоривания с нечеткой настройкой параметров
- 77-30569/347444 Разработка адаптивного алгоритма релейного управления двухуровневым демпфированием подвески многоосных колесных машин
- Разработка адаптивного закона релейного управления трехуровневым демпфированием упруго-демпфирующих элементов подвески многоосных колесных машин
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||