научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2013
DOI: 10.7463/0213.0531045
УДК.67.02, 004.942, 519.178
Россия, МГТУ им. Н.Э. Баумана
В проектной и производственной практике инженеров различной специализации часто возникает задача синтеза рационального линейного порядка. Она имеет очень простую формальную постановку. Дана совокупность линейных порядков P={P1,P2,...,Pn}, определенных на одном множестве объектов X. P представляет собой бесструктурное множество, у которого элементы Pi не связаны никакими отношениями друг с другом. В задаче требуется выбрать из P линейный порядок, который удовлетворяет системе представлений эксперта о разумной или непротиворечивой последовательности объектов, принадлежащих X (рис. 1). Следуя терминологической традиции, сложившейся в теории принятия решений, совокупность P будем называть исходным множеством альтернатив (ИМА), а ее элементы Pi – альтернативами.

Множество задач этого типа приходится решать в процессе технологической подготовки машиностроительного производства. Приведем два важных примера. Первый из них относится к разработке маршрутного технологического процесса обработки детали. Здесь множество X представляет собой объем обработки – совокупность технологических операторов, которые обеспечивают генерацию детали заданной геометрии и точности. P – это множество технологически реализуемых последовательностей операторов (линейных порядков). Popt – лучшая последовательность в данной производственной ситуации.
Другой пример взят из практики механосборочного производства и связан с разработкой технологических процессов сборки. В этой задаче X – это множество деталей, а исходным множеством альтернатив служат все конструктивно реализуемые последовательности сборки, которые допускает изделие по условиям базирования, геометрической разрешимости и размерным связям [3]. Из данного множества требуется выбрать последовательность сборки, лучшую по соображениям технологического удобства или экономической целесообразности.
Упомянем две особенности задачи выбора рационального упорядочения, которые усложняют ее эффективное решение классическими методами исследования операций или теории принятия решений. Во-первых, высокая комбинаторная мощность исходного множества альтернатив, что делает затруднительным применение аппарата ординальной теории принятия решений. Во-вторых, латентная сложность каждой альтернативы, которая становится очевидной при любой попытке выразить свойство упорядочения числом (значением критерия) или набором чисел (вектором критериев). Рассмотрим метод генерации рационального упорядочения, который позволяет избежать парных сравнений многочисленных альтернатив и свободен от упрощений, неизбежных при любой попытке формализовать сложное качество при помощи критерия или вектора критериев.
Метод рационального упорядочения основан на так называемом στ‑разложении множеств, состоящих из линейных порядков. Подробное изложение необходимого математического аппарата изложено в [2]. В данной работе приведем краткое описание основных понятий, необходимых для понимания текста. В силу очевидного соответствия между линейными порядками и перестановками будем иногда пользоваться последним более кратким наименованием.
Обозначим через Λ(X) – множество всех отношений порядка на множестве X. Множество Λ(X) само является упорядоченным, в качестве отношения порядка на нем выступает теоретико-множеcтвенное включение. Максимальными элементами в Λ(X) служат линейные порядки на X и только они. В Λ(X) существует наименьший элемент – это дискретный порядок на X, в котором отсутствуют упорядоченные пары. Элементы Λ(X) будем обозначать через λ и добавлять при необходимости различные нижние индексы.
Добавим к Λ(X) максимальный элемент 1, который не несет порядкового содержания, а представляет собой абстрактный элемент, необходимый для регуляризации этой структуры. Можно доказать (см. [4]), что доопределенное таким образом множество Λ(X) представляет собой решетку – алгебраическую структуру, замкнутую относительно операций решеточного пересечения и объединения. Введем обозначение Λn = Λ(X), |X| = n.
Пусть Sn – множество всех перестановок степени n (линейных порядков из n элементов), B(Sn ) – его булеан. Известно, что булеан любого множества является решеткой [1]. Рассмотрим отображения σ : Λn → B(Sn ) и τ : B(Sn ) → Λn. Отображение σ каждому упорядоченному множеству из Λnставит в соответствие совокупность всех его линейных продолжений. В B(Sn ) они представлены в виде перестановок. Будем считать, что образом максимального элемента решетки Λnслужит наименьший элемент В(Sn ) – пустое множество. Отображение τ каждому элементу Р изВ(Sn ) сопоставляет частичный порядок τ(P) ∈ Λn, который представляет собой пересечение линейных порядков, принадлежащих P. Пусть пустому множеству перестановок соответствует максимальный элемент в Λn, то есть τ(Ø)=1 ∈ Λn.
Даже для относительно небольших значений n решетки Sn и Λn представляют собой очень громоздкие объекты, размеры которых стремительно растут с увеличением n. На рис. 2 показаны эти объекты и их взаимные отображения σ и τ для самой малой размерности, равной 2.
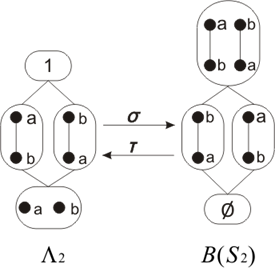
Рассмотрим эти отображения на двух простых примерах. Пусть Р ∈ В(S4 ) и P = {1234, 1324, 1432}. Элементы из Рпредставляют следующие линейные порядки a1 = {1<2<4<3}, a2 = {1<3<2<4}, a3 = {1<4<3<2}. Найдем пересечение трех линейных порядков τ(P) = a1∩a2∩a3, τ(P) = {(1<2), (1<4), (1<3)}.
Если λ ∈ Λ4 = {1<2, 3<4}, то σ(λ) = {1234, 3412, 1342, 1324, 3124, 3142}.
В [2] показано, что отображения σ и τ обладают свойствами:
1. для любых А, B ∈ Λn таких, что A ≤ В выполняется σ(A) ≥ σ(B);
2. для любых P, R ∈ В(Sn ) таких, что Р ≤ R выполняется τ(P) ≥ τ(R);
3. τ(σ(А)) ≥ А для всех A ∈ Λn;
4. σ(τ(P)) ≥ P для всех Р ∈ B(Sn ).
Пара отображений (σ, τ), для которой выполняются свойства 1 – 4, называется соответствием Галуа. Так как область значений и область определения отображений σ и τ являются решетками, то композиции отображений τσ и στ являются операторами замыканий на Λn и B(Sn) соответственно [1].
Элементы А ∈ Λn, для которых справедиво τ(σ(А)) =А, называются τσ-замкнутыми. Элементы Р ∈ B(Sn ) с условием σ(τ(P)) = P – στ-замкнутыми. Таковые порядки и перестановки будем именовать в дальнейшем просто замкнутыми.
Множество всех τσ-замкнутых элементов Λn называется частным по замыканию оператора τσ и обозначается Λn / τσ. Для этого множества справедливо соотношение Λn / τσ = τ(В(Sn )).
Множество всех στ-замкнутых элементов из В(Sn ) называется частным по замыканию оператора στ и обозначается В(Sn ) / στ.Для него справедливо соотношение В(Sn ) / στ = σ(Λn ). Множества Λn / τσ и В(Sn ) / στ – антиизоморфные, а отображенияσ и τ, действующие на них, взаимно обратные.
Любое частично упорядоченное множество есть пересечение некоторой совокупности линейных порядков, например множества всех линейных продолжений его самого. Поэтомукаждый элемент из Λnявляется τσ-замкнутым и Λn = Λn / τσ.
Частное В(Sn ) / στ имеет более сложную структуру. Замкнутыми элементами в нем являются такие множества перестановок, которые представляют собой линейные доупорядочения, порожденные некоторым частичным порядком. Пересечение любых двух замкнутых элементов, в свою очередь, является замкнутым и принадлежит частномуВ(Sn ) / στ. Так как σ(1) = 0, то и наименьший элемент решетки В(Sn )– замкнутый.
На рис. 3 показана решетка В(S3 ). Атомами этой решетки служат одноэлементные множества перестановок, которые на данном рисунке обозначены числами: 1 – (3,2,1); 2 – (2,3,1); 3 – (3,1,2); 4 – (1,3,2); 5 – (1,2,3); 6 – (2,1,3). Черные вершины обозначают замкнутые στ-элементы В(S3 ).
В [2] доказана несложная, но принципиально важная теорема, утверждающая, что любой элемент решетки В(Sn ) можно представить в виде объединенияστ-замкнутых элементов. Представление произвольного множества перестановок в виде объединения στ-замкнутых множеств будем называть στ-разложением. Например, 1,3,5 = 1,3 + 5 или 2,3,4,5,6 = 2,5,6 + 3,4,5 (см. рис. 3).
Поскольку решетка В(Sn ) – атомарная, а любой ее атом представляет собой замкнутый элемент, то στ-разложение в общем случае может быть реализована несколькими разными способами. Например, 2,3,4,5,6 = 2,5,6 + 3,4,5=4,5,6+3,4+2=5,6+2,6+3,4 и др.

Разложение на στ-замкнутые подмножества дает наглядный и компактный способ представления таких чрезвычайно громоздких образований, которыми являются множества перестановок. Обратимся к примеру, показанному на рис. 4. На этом рисунке изображено множество перестановок Р и отмечено одно из его στ-разложений на составляющие P' и P'' , которые обведены сплошной и штриховой линией соответственно. Ниже показаны два упорядоченных множества A1 и А2 таких, что σ(A1) = P' и σ(А2) = P''.
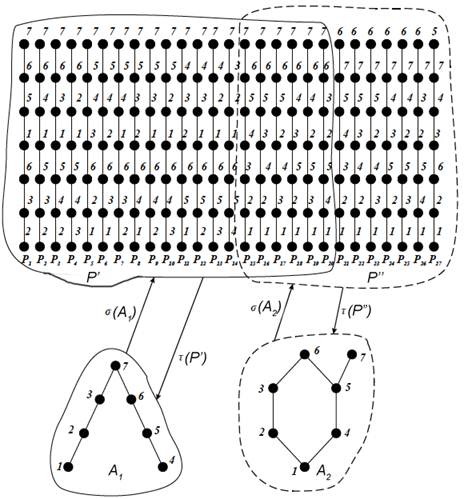
Рис. 4. Множество перестановок и его στ-разложение
Предложенный способ представления множеств перестановок обладает несколькими несомненными теоретическими и практическими достоинствами. Самые главные из них – это наглядность и высокая степень сжатия информации, реализуемое без потерь и искажений (lossless).
Разложение на στ-замкнутые подмножества и их представление в виде частичных порядков дает основания для постановки различных многошаговых процедур принятия рациональных решений, в которых сведения, полученные от ЛПР, используются для последовательного доупорядочения системы предпочтений. Дополнительные данные о порядковых отношениях элементов дает более глубокое исследование ситуации принятия решений. В этой экспертизе «операционное поле» ЛПР ограничивается несравнимыми элементами στ-разложения. Все сравнимые объекты исключаются из обработки, что существенно упрощает задачу выбора.
Полученная порядковая информация вносится в στ-разложение, что делает его более структурированным. Обозначим A στ-разложение до экспертизы, а B – после нее. ![]() , где
, где ![]() – результат парного сравнения деталей i и j. Поскольку
– результат парного сравнения деталей i и j. Поскольку ![]() , то есть множество перестановок сокращается. Далее, находится новое στ-разложение для редуцированного множества
, то есть множество перестановок сокращается. Далее, находится новое στ-разложение для редуцированного множества ![]() и его представление предъявляется для следующей проверки технолога и т.д.
и его представление предъявляется для следующей проверки технолога и т.д.

Рис. 5. Частичный порядок и его линейные доупорядочения
Проиллюстируем приведенные рассуждения простым примером, показанном на рис. 5. На этом рисунке изображен пятиэлементный частичный порядок и все его линейные продолжения. В приведенном множестве есть четыре пары несравнимых элементов: 1||3, 5||4, 5||3, 1||4. Любой вариант сравнения данных антицепей является допустимым и согласуется с исходной порядковой структурой. Каждое такое предпочтение влечет за собой повышение меры линейности частичного порядка и сокращение множества согласованных с ним линейных порядков. На рис. 6 показаны все допустимые варианты сравнения несравнимых пар и множества линейных порядков, которые порождают их включение в исходную структуру.
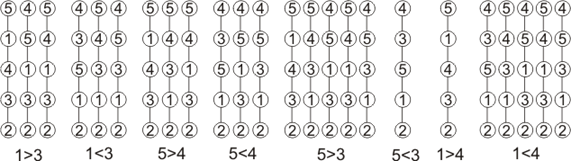
Рис. 6. Сравнение несравнимых пар и их линейные продолжения
Принципиальную возможность генерации линейных продолжений гарантирует классическая теорема Шпильрайна, гласящая, что любой частичный порядок может быть продолжен до линейного упорядочения на том же множестве элементов [1]. Алгоритм генерации всех линейных продолжений заданного частичного порядка приводится в [5].
Одна из возможных многошаговых процедур выбора рациональной последовательности, основанная на технике στ-разложения множеств перестановок, показана на рис. 7.

Рис. 7. Многошаговая процедура принятия рациональных решений
Рассмотрим эту процедуру применительно к задаче выбора рациональной последовательности сборки механической системы (машины или прибора). Пусть Р есть множество последовательностей сборки некоторого изделия, которые допускает его конструкция по условиям базирования и геометрической разрешимости [3]. Из этого множества необходимо исключить такие последовательности, которые не удовлетворяют условиям технологичности, экономичности и др.
Будем считать, что найдено разложение множества P и определены все его пары несравнимых элементов (антицепей). Лицу принимающему решение, которым в данной ситуации служит технолог, предлагается для анализа пара несравнимых элементов στ-разложения, для которой он должен выбрать одну из следующих возможностей:
1. i > j, деталь i должна быть установлена после детали j;
2. i < j, деталь i устанавливается раньше детали j;
3. i = j, детали i и j должны устанавливаться одновременно;
4. Отказ от сравнения. и выбор другой несравнимой пары.
Полученная от ЛПР порядковая информация вносится в разложение, находятся все линейные продолжения нового доопределенного частичного порядка, находится разложения сокращенного множества перестановок, которое предъявляется ЛПР для оценки.
Количество итераций этой процедуры можно существенно сократить за счет выбора наиболее информативных. Рассмотрим способ, позволяющий исключить из рассмотрения заведомо нерациональные пары.
Каждой паре несравнимых элементов a = {i || j} ∈ A, где А – некоторое упорядоченное множество, принадлежащее στ-разложению, поставим в соответствие тройку (a1, a2, a3), которую назовем вектором исходов. Координаты вектора исходов подсчитаем по формулам:
 , если a = {i > j};
, если a = {i > j};
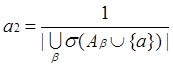 , если a = {i <j};
, если a = {i <j};
 , если a = {i =j}.
, если a = {i =j}.
Объединение линейных продолжений ведется по таким индексам ![]() , для которых упорядоченные множества
, для которых упорядоченные множества ![]() и
и ![]() не образуют контуров с упорядоченной парой {i, j}, а 𝜀 представляет собой эквивалентность, стабильную на эквивалентность 𝜀 стабильна на
не образуют контуров с упорядоченной парой {i, j}, а 𝜀 представляет собой эквивалентность, стабильную на эквивалентность 𝜀 стабильна на ![]() .
.
На множестве пар несравнимых элементов разложения можно ввести отношение доминирования. Будем говорить, что пара a' = {i, j} доминирует пару а"= {m, n}, если вектор исходов ![]() доминирует по Парето вектор исходов
доминирует по Парето вектор исходов ![]() . Ясно, что альтернативы, вектор исходов которых является оптимальным по Парето, в большей степени «доупорядочивают» множество
. Ясно, что альтернативы, вектор исходов которых является оптимальным по Парето, в большей степени «доупорядочивают» множество ![]() . Если для оценки ЛПР предлагать пары, которые имеют Парето-оптимальный вектор исходов, то для выбора оптимальной перестановки потребуется меньше итераций, чем для случая
. Если для оценки ЛПР предлагать пары, которые имеют Парето-оптимальный вектор исходов, то для выбора оптимальной перестановки потребуется меньше итераций, чем для случая
Выводы
1. Разложение на στ-замкнутые подмножества представляет собой компактный и удобный для автоматизированной обработки способ представления множеств перестановок высокой мощности. Оно, по сути дела, является способом сжатия информации без потерь и искажений (lossless). Объединение всех линейных продолжений частичных порядков, входящих в разложение, восстанавливает исходное множество перестановок в аутентичной форме.
2. Техника στ-разложения может быть использована для организации различных многошаговых процедур принятия решений, в которых выбор рациональной перестановки выполняется в диалоге с ЛПР за счет итерационного доупорядочения исходной структуры предпочтений.
3. Выбор наиболее информативных пар несравнимых элементов позволяет существенно сократить трудоемкость процедуры и минимизировать число обращений к ЛПР. На множестве антицепей можно ввести доминирование по Парето, что позволяет отбросить заведомо худшие альтернативы. Решение задачи в общем случае представляется очень сложным. В следующей статье автор планирует описать различные информационные ситуации, допускающие полное или частичное решение задачи выбора наиболее информативной пары.
Список литературы
- Айгнер М. Комбинаторная теория: пер. с англ. М.: Мир, 1982. 560 с.
- Божко А.Н. Метод диалогового упорядочения альтернатив // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2010. № 5. Режим доступа: http://technomag.edu.ru/doc/142892.html (дата обращения 27.01.2012).
- Буловский П.И. Основы сборки приборов. М.: Машиностроение, 1970. 200 c.
- Гретцер Г. Общая теория решеток : пер. с англ. М.: Мир, 1982. 456 c.
- Розен В.В. Цель – оптимальность – решение (математические модели принятия оптимальных решений). М.: Радио и связь, 1982. 168 c.
Публикации с ключевыми словами: принятие решений, перестановка, последовательность сборки, линейный порядок, ЛПР, στ-разложение, соответствие Галуа
Публикации со словами: принятие решений, перестановка, последовательность сборки, линейный порядок, ЛПР, στ-разложение, соответствие Галуа
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



