научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#2 Февраль 2005
А.Л. Глебов, канд. физ.-мат. наук, НИИ систем автоматизированного проектирования РЭА и СБИС Российской Академии наук
SP-BDD-модель цифровых КМОП-схем и ее приложения в оптимизации и моделировании
В работе рассмотрено новое BDD-представление для последовательно-параллельных цепей (SP-BDD). SP-BDD модель может эффективно использоваться в задачах моделирования, оптимизации и логического синтеза для КМОП-схем. Описываются основные алгоритмы экстракции SP-BDD и работы с ними. Рассмотрены приложение модели к задаче переупорядочения транзисторов, а также другие приложения.
1. Введение
Первоначально SP-BDD (Series-Parallel Binary Decision Diagram) была разработана как модель последовательно-параллельной цепи (SP-цепи) [1]. SP-цепи широко используются в цифровых МОП-схемах в качестве pull-up и pull-down цепей (связь по питанию и связь по земле). Каждая SP-цепь реализует некоторую булеву функцию. Экстракция SP-цепей и соответствующих булевых функций из транзисторного нетлиста (списка электрических связей), равно как и разработка удобного представления для них, является задачей, важной для следующих приложений:
· переупорядочения транзисторов в pull-up/ pull-down цепях для уменьшения мощности или задержек [2];
· использования единой модели SP-цепи вместо моделей отдельных транзисторов в переключательном моделировании [3];
· проверки комплементарности пары pull-up и pull-down цепочек с одним выходным узлом и объединение их в один логический КМОП-вентиль для последующего перехода к логическому моделированию;
· получения булевой функции логического блока (группы логических вентилей) для последующего ресинтеза или формальной верификации.
Известны различные представления SP-цепей, используемые для тех или иных конкретных задач [4, 5]. Но ни одно из них не является удобным для всех перечисленных приложений.
В данной работе описано новое представление для SP-цепи и соответствующей булевой функции, основанное на BDD (диаграммах двоичных решений) специального вида (мы назвали их SP-BDD). Мы предлагаем также алгоритм экстракции SP-BDD из транзисторного нетлиста. Данное представление позволяет эффективно манипулировать с SP-цепями в процессе переупорядочения транзисторов, производить экстракцию логики и т.д.
SP-BDD представляет не только булеву функцию SP-цепи, но также ее электрическую схему (нетлист). На множестве транзисторов SP-цепи существует естественный частичный порядок. Мы используем этот частичный порядок при построении SP-BDD представления.
Транзисторный нетлист представляет собой неориентированный граф (схемный граф) с вершинами для узлов схемы и ребрами для транзисторов схемы. Пусть a, b - транзисторы SP-цепи. Будем говорить, что а < b ("а предшествует b"), если в схемном графе существует несамопересекающийся путь, начинающийся в источнике, заканчивающийся в выходе и содержащий а и b, причем а раньше b. (Источником и выходом мы называем здесь терминалы SP-цепи соответственно с постоянным и переменным потенциалами.) Можно показать, что:
· отношение "<" является частичным порядком;
· структура SP-цепи полностью определяется заданием списка транзисторов и частичного порядка для них.
Далее указанный частичный порядок, как будет показано ниже, можно вложить в некоторый естественным образом определенный линейный порядок.
BDD и ее различные модификации являются эффективным и широко используемым представлением для булевых функций [6, 7]. ROBDD (редуцированные упорядоченные BDD) - наиболее используемая модификация, для которой разработано много эффективных алгоритмов.
Для заданной булевой функции и заданного (произвольного) порядка аргументов существует единственная ROBDD. Возьмем SP-цепь и построим ROBDD для ее булевой функции. Если в качестве порядка аргументов возьмем вышеуказанный линейный порядок транзисторов, получим SP-BDD.
Отметим два замечательных свойства SP-BDD:
1. SP-BDD имеет минимальный размер, так как она содержит в точности одну вершину для каждого аргумента (транзистора).
2. SP-BDD для заданной SP-цепи не единственна, поскольку SP-цепь может содержать параллельные ветви. Однако для пары комплементарных pull-up/ pull-down цепей SP-BDD строится единственным образом. Следовательно, SP-BDD является каноническим представлением для комплементарного логического КМОП-вентиля.
В данной работе представлены основные алгоритмы для конструирования и работы с SP-BDD. Представлен также алгоритм экстракции SP-цепи и соответствующего SP-BDD представления из заданного транзисторного нетлиста. В качестве первого применения рассмотрено переупорядочение транзисторов в произвольных pull-up/pull-down цепях.
2. SP-цепи и SP-BDD представление
Часть цифровой КМОП-схемы (или вся схема) может быть, как правило, разделена на pull-up и pull-down цепи. (Для краткости будем называть их pupd-цепями.) Pupd-цепь — это схема с двумя терминалами. Один из них (назовем его источником, source) присоединен к узлу-источнику (узел с постоянным потенциалом, потенциалом питания или земли). Другой (назовем его выходом, output) присоединен к выходному узлу (узел с переменным потенциалом).
Каждая pupd-цепь реализует некоторую булеву функцию. Если рассматривать состояние каждого транзистора pupd-цепи как независимую переменную (1 — проводящее состояние, 0 — непроводящее состояние), то булева функция принимает значение 1, если pupd-цепь проводит, и значение 0 - в противном случае.
В качестве pupd-цепи чаще всего используется SP-цепь, которая определяется рекурсивно:
A. Один МОП-транзистор - это SP-цепь с любым из двух терминалов (исток, сток) в качестве источника и с другим в качестве выхода.
B. Если X, Y — SP-цепи, то Z = series (X, Y) - также SP-цепь, где по определению series(),
X.source и Z.source соединены,
X.output и Y.source соединены,
Y.output и Z.output соединены.
С. Если X, Y - SP-цепи, то Z = parallel (X, Y) - также SP-цепь, где по определению parallel(),
X. source, Y. source и Z.source соединены,
X. output, Y. output и Z.output соединены.
Это определение иллюстрируется рис. 1.
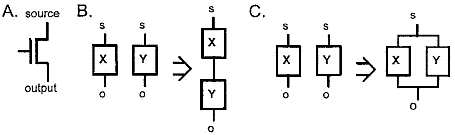
Рис. 1. Рекурсивное определение SP-цепи
Здесь и далее мы будем рассматривать pupd-цепи, являющиеся SP-цепями и содержащие транзисторы одного типа (n или p).
Мы можем доопределить вышеупомянутый частичный порядок "<" на множестве транзисторов SP-цепи до полного порядка "<<" следующим образом. Во-первых, если a < b, то a << b. Во-вторых, добавим следующее условие: если SP-цепь содержит Z = parallel (X, Y), X, Y-также SP-цепи, то
или а < b для любых а из X и b из Y.
или b < а для любых а из X и b из Y.
Можно показать, что при наложении дополнительного требования транзитивности полный порядок "<<" является линейным порядком для транзисторов SP-цепи. Этот линейный порядок совместим:
· с частичным порядком для этой SP-цепи;
· с одним из возможных частичных порядков для комплементарной SP-цепи (получаем комплементарную SP-цепь заменой series<->parallel).
Для заданной булевой функции и заданного порядка аргументов существует единственная ROBDD. Пусть есть SP-цепь. Если при построении для нее ROBDD мы в качестве порядка аргументов возьмем один из возможных линейных порядков "<<", то получим SP-BDD. Много полезных свойств SP-BDD вытекают из метода ее построения, описанного ниже.
3. Основные алгоритмы для построения SP-BDD
Ниже дается описание основных алгоритмов для построения SP-BDD представления SP-цепи. (Ниже рассматриваются только SP-BDD, поэтому будем для краткости вместо SP-BDD использовать термин BDD.)
Каждая вершина v имеет в BDD две вершины-сына: low(v) обозначает 0-сына (low-son), a high(v) обозначает 1-сына (high-son). Если X - BDD, то root(X) означает ее корневую вершину. Для описания алгоритмов будем использовать С-подобный псевдокод. Каждая вершина в BDD описывается структурой данных, определяемой следующим образом (по аналогии с [6]):
struct vertex { /* вершина BDD */
struct vertex *low, /* указатель на 0-сына */
*high; /* указатель на 1-сына */
int transistor, /* индекс транзистора */
node /* индекс предыдущего узла*/
index /* индекс вершины BDD */
… /* вспомогательные поля */
Мы предполагаем, что все транзисторы в схеме, содержащей рассматриваемую pupd-цепь, пронумерованы неотрицательными числами (то же для узлов). Кроме того, BDD в целом нуждается в следующей информации:
struct pupd_network { /* BDD для pupd-цепи */
struct vertex *root; /* указатель на корневую
вершину */
int type, /* тип транзисторов: 0 - n,
l – р */
output__node; /* индекс выходного узла */
В отличие от [6] мы не храним в памяти вершины-листья BDD. Мы предполагаем только, что каждая вершина, для которой vertex.low=NULL, имеет в качестве 0-сына одну из двух вершин-листьев (лист "0"). Аналогично, каждая вершина с vertex.high=NULL имеет в качестве 1-сына другую вершину-лист (лист "1").
Простейший вариант SP-цепи содержит один транзистор. Соответствующая BDD состоит из одной вершины v с low (v)=0 и high(v)=l (рис. 2).

Рис.2. SP-BDD для одиночного транзистора
Рассмотрим некоторые полезные операции над SP-BDD. Пусть X — BDD для произвольной SP-цепи. Пусть Y — подграф X, порождаемый вершинами (не листьями) X с a.index <= vertex.index <= b.index, где а, b - некоторые вершины (не листья) X. В этом случае мы называем Y интервалом X: Y=interval(X, a, b). Далее будем использовать присваивание low(Y)=v вместо следующего псевдокода:
for (all vertices of Y) {
if (low(vertex) is not in Y)
vertex.low = &v;
Аналогично, high(F) = v означает:
for (all vertices of Y) {
if (high(vertex) is not in Y)
vertex.high = &v;
Мы используем графические обозначения для Y = interval (X, a, b), low(Y), high(Y), показанные на рис. 3.
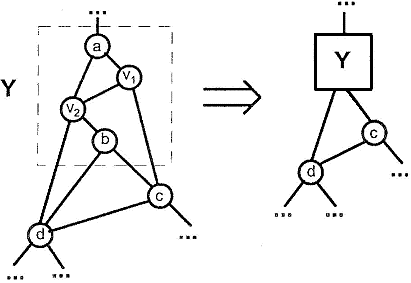
Рис.3. Графические обозначения для Y = interval (X, a, b); low (Y) = d; high (Y) = c
Для краткости мы будем часто использовать одно и то же обозначение для разных объектов. Например, X может обозначать как SP-цепь, так и соответствующую BDD, а может обозначать либо вершину BDD, либо соответствующий аргумент булевой функции, либо соответствующий транзистор в SP-цепи.
Если X— BDD, a v — вершина X, то можно разделить X на две BDD F и Z, где root(Y)=root(X) и root(Z)=v. Для этой операции будем использовать обозначение:
(Y Z) = divide (X, v).
С другой стороны, мы можем объединить несколько BDD А, В, С в один ориентированный граф со следующим порядком вершин: сначала все вершины А, затем все вершины В и т.д. Для этой операции будем использовать обозначение:
Х - order (А, В, С);
(После этой операции Х еще не является BDD. Для преобразования Х в BDD мы должны сделать корневые вершины B, С сыновьями некоторых других вершин с меньшими индексами.)
Мы можем также объединить две BDD Х и Y в один ориентированный граф путем вставления всех вершин Y после вершины v, заданной в X, и всеми последующими вершинами из X:
Z = insert (X, v, Y);
(После этой операции все соединения между вершинами в X сохраняются.) Пусть Z = series (X, Y). На языке BDD это выглядит так (рис. 4):
Z = order (X, Y);
high(X) = root (Y);
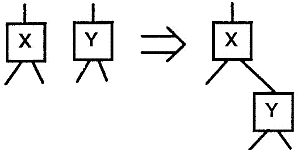
Рис.4. Z=series (X, Y)
Пусть Z = parallel (X, Y). На языке BDD это выглядит так (рис. 5):
Z = order (X, У);
low(X) = root(y);
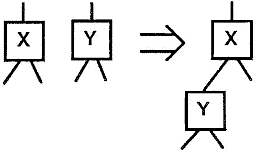
Рис. 5. Z=parallel (X, Y)
В силу неединственности SP-BDD модели для параллельного соединения мы можем описать ту же SP-цепь по-другому:
Z = order (Y, X);
low(Y) = root (X);
Следовательно, на языке BDD, parallel(X, Y) и parallel(X, Y) - это две разные BDD, соответствующие одной SP-цепи.
Пусть D - последовательное соединение А, В, С:
D = series (series (А, В), С);
Образуем новую SP-цепь F путем вставления SP-цепи Е, соединенной параллельно с В. Пусть даны b=root(B), c=root(C). Тогда на языке BDD (рис. 6):
(D С) = divide (D, с);
(А, В) = divide (D, b);
D = parallel (B, Е);
D = series (A, D);
F = series (D, С).
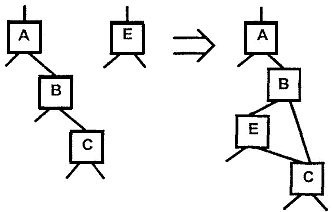
Рис. 6. Вставление Е, соединенной с В параллельно
Рассмотрим в схемном графе несамопересекающийся путь, содержащий последовательность узлов и транзисторов:
no[0]-tr[0]-...-no[i]-tr[i]-...-no[n-l]-tr[n-l]-no[n].
Мы можем построить BDD для этого пути, т.е. для SP-цепи, содержащей только транзисторы этого пути, при этом по[0] будет источником, а по [n] — выходом:
X - make_bdd (path);
Эта операция описывается следующим псевдокодом:
for (i=0); i<n; i++) {
create (v[i]); /* создать новую вершину */
v[i].transistor = tr[i];
v[i].node = node[i];
v[i]. index = i;
v[i-l], low = NULL;
v[i-l].high = &v[i];
}
}
v[n-l], low = NULL;
v[n-l].high = NULL;
create (X); /* создать новую BDD */
X. root = &v[0];
X. type = tr[0].type;
X. output_node = no[n];
Опишем, наконец, операцию, которая будет использована при экстракции pupd-цепей. Пусть X — BDD для SP-цепи, содержащей путь с первым транзистором а и последним транзистором b, a < b или а = b. Пусть Y-BDD для другой SP-цепи, которая должна быть вставлена в X параллельно вышеупомянутому пути. Предполагается также, что X не содержит какого-либо другого пути, параллельного упомянутому. Мы используем следующее обозначение для этой операции:
X = include (X, а, b, Y);
Она осуществляется следующим образом:
I = interval (X, а, b);
if (b.low = = NULL && b.high = = NULL) {
Z = order (X, Y);
low (I) = root (Y);
}
else {
Z = insert (X, b, Y);
low (Y) = low (b); high (Y) = high (b);
low (I) = root (Y);
}
X = Z;
4. Алгоритм экстракции SP-цепей
Опишем теперь алгоритм экстракции pupd-цепей из транзисторного нетлиста, а также формирования их SP-BDD модели. Эта модель может, в частности, быть использована для:
· операций с pupd-цепью при переупорядочении транзисторов;
· экстракции булевой функции логических вентилей или их групп.
Данный алгоритм производит последовательную обработку всех DCCC (DC Connected Component) КМОП-схемы. Обработка одной DCCC начинается с поиска исходного пути от узла источника (земля или питание) до выходного узла (узел, к которому присоединены истоки/стоки транзисторов обоих типов). Для исходного пути формируется SP-BDD. После этого делается последовательность шагов. Каждый шаг содержит:
· поиск хорды (т.е. нового пути, соединяющего любые два узла ранее найденного пути);
· формирование SP-BDD для хорды;
· вставление SP-BDD для хорды в текущую SP-BDD для pupd-цепи.
Производится также обнаружение мостов (SP-цепь не может содержать мостов). Пример pupd-цепи и соответствующей SP-BDD, сформированной данным алгоритмом, показан на рис. 7.

Рис.7. Pull-up цепь и два варианта ее SP-BDD, соответствующие различной структуре комплементарной pull-down цепи
5. Первое приложение: переупорядочение транзисторов
Переупорядочение транзисторов в pupd-цепях — это эффективный инструмент для снижения мощности и задержек в КМОП-схемах [1, 2]. Однако все алгоритмы переупорядочения, найденные нами в публикациях, ориентированы на использование стандартных ячеек. Эти алгоритмы способны переупорядочить транзисторы только в простых цепочках последовательно соединенных транзисторов (это соответствует переназначению входов в стандартных ячейках). Например, эти алгоритмы способны переупорядочить транзисторы в n-входовых вентилях NAND и NOR.
С другой стороны, максимальная длина последовательной цепочки транзисторов в больших КМОП-вентилях растет с 5 (для 2-микрометровых проектов) до 7 (для субмикронных проектов) [8]. Поэтому проблема переупорядочения транзисторов в произвольных pupd-цепях является крайне актуальной.
Мы предлагаем здесь алгоритм переупорядочения транзисторов с целью минимизации мощности при ограничениях на задержки.
Пусть Х- SP-BDD, a v - вершина в X. Для предыдущей и последующей вершин X будем использовать обозначения: previous(Z, v), next(Z, v).
Рассмотрим переупорядочение транзисторов в pupd-цепи как последовательность элементарных перестановок. Каждая элементарная перестановка (назовем эту операцию "series_change") производится следующим образом.
Пусть X — pupd-цепь (или соответствующая SP-BDD) и пусть Y- подсхемах такая, что Y=series(A, В), где А или состоит из одного транзистора, или является параллельным соединением двух или более SP-цепей (то же для В). Операция series_change производит следующую замену:
Series (A, В) -> series (B, А).
Если А первоначально присоединена к узлу node_a (как к узлу-источнику) и к узлу node_b (как к выходному узлу), а В первоначально присоединена к node_b и node__c, то series_change включает следующие шаги:
· отсоединить А от node_a и nods_b;
· отсоединить В от node_b и node_c;
· присоединить В к node_a и node_b;
· присоединить А к node_b и node_c.
Для текущего состояния pupd-цепи Х возможны в точности n различных элементарных перестановок, где n - число внутренних узлов в X.
На языке SP-BDD производим элементарную перестановку путем перестановки двух соседних интервалов BDD. Пример элементарной перестановки показан на рис. 8.

Рис.8. Элементарная перестановка B<->C на языке SP-целей (А) и на языке SP
Алгоритм переупорядочения осуществляет в pupd— цепях последовательность элементарных перестановок. Все элементарные перестановки, возможные из текущего состояния pupd-цепи, упорядочены в силу упорядоченности SP-BDD. Поэтому выбор следующей возможной элементарной перестановки осуществляется простым способом.
Трудно точно предсказать, как элементарная перестановка двух произвольных SP-цепей повлияет на мощность и задержки. Поэтому для определения этого влияния в сегодняшней версии алгоритма производится вычисление мощности и задержек до и после элементарной перестановки (или нескольких элементарных перестановок, производимых одновременно в различных DCCC). При этом используются быстрые алгоритмы расчета мощности и задержек, также основанные на SP-BDD модели.
Элементарная перестановка меняет узловые емкости и пути их зарядки и разрядки. Поэтому оптимальные размеры транзисторов до и после элементарной перестановки, как правило, существенно различны. В силу этого производим переупорядочение для схемы с минимальными размерами транзисторов. После переупорядочения производится оптимизация по размерам транзисторов, с целью удовлетворить ограничениям и окончательно минимизировать мощность.
Мы приводим здесь типичные результаты тестирования алгоритма переупорядочения. Использованные тестовые схемы содержали pupd-цепи различного размера. Для каждой схемы оптимизация по размерам транзисторов, минимизирующая мощность при ограничениях на задержки, производилась дважды: до и после переупорядочения. Оба результата сравнивались между собой.
Тестовые последовательности, использованные для расчета мощности, генерировались случайным образом.
Результаты тестирования приведены в таблице. Эти результаты показывают высокую эффективность алгоритма переупорядочения (средний выигрыш в мощности в результате переупорядочения составляет 13 %, в некоторых случаях — значительно больше).
Таблица
Результаты параметрической оптимизации до и после переупорядочения
|
Схема |
Исходная МОЩНОСТЬ |
Конечная МОЩНОСТЬ |
Уменьшение |
|
nand4 |
15.9 |
13.3 |
17% |
|
C17 |
14.1 |
13.8 |
2% |
|
mx |
41.4 |
40.3 |
3% |
|
ao221h |
46.4 |
43.3 |
7% |
|
ao221s |
46.1 |
39.5 |
14% |
|
ao321h |
63.2 |
51.8 |
18% |
|
ao32Is |
69.5 |
50.5 |
27% |
|
gate7 |
55.7 |
46.4 |
17% |
Надо отметить, что схемы АО221Н и AO221S являются различными реализациями одной и той же булевой функции. То же справедливо для схем АО321Н и AO321S. Это показывает, что для использования в низкомощных схемах сложные КМОП-вентили с инвертором на выходе являются более предпочтительными, чем несколько вентилей примерно равной сложности, реализующие ту же булеву функцию.
Пример исходного и конечного (после переупорядочения) КМОП-вентиля показан на рис. 9.

Рис.9. Исходная схема (gate7) и результат переупорядочивания
* * *
В данной работе описано новое эффективное представление для последовательно-параллельных цепей. Это представление основано на BDD специального вида (SP-BDD). SP-BDD модель является эффективным инструментом для канонического представления цифровых КМОП-вентилей и различных преобразований над ними. Описаны основные алгоритмы работы с SP-BDD, а также приложение этой модели к проблеме переупорядочения транзисторов.
Разработан также ряд других приложений SP-BDD модели к моделированию и оптимизации цифровых КМОП-схем. Выше упоминалось использование SP-BDD для разработки быстрых алгоритмов переключательного моделирования, расчета мощности и задержек для КМОП-схем [9]. Сеть SP-BDD может быть использована как удобное представление для КМОП-схемы произвольного размера. Разработаны также эффективные алгоритмы экстракции булевых функций, а также оптимального ресинтеза КМОП-схем, в том числе низкомощных [10]. Указанный ресинтез значительно улучшает параметры схем, предварительно синтезированных лучшими программами логического синтеза. Простой пример результата ресинтеза показан на рис. 10.
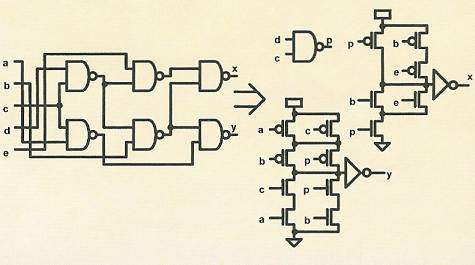
Рис.10. Исходная схема (c17) и результат ресинтеза низкомощной схемы, основанного на использовании SP-BDD модели
Список литературы
1. Glebov A.L., Blaauw D., Jones L.G. Transistor Reordering for Low Power CMOS Gates Using an SP-BDD Representation // Intern. Symp. on Low Power Design, Dana Point (CA), pp. 161—165.
2. Carlson B.S., Chen C.Y.R. Performance Enhancement of CMOS VLSI Circuits by Transistor Reordering / Proc. of 30th DAC. 1993. P. 361-366.
3. Bryant R.E. Boolean Analysis of MOS Circuits // IEEE Trans, on CAD. 1987, v. 6. Pp. 634-649.
4. Boehner M. LOGEX - An Automatic Logic Extractor from Transistor to Gate Level for CMOS Technology / Proc. of 25th DAC, 1988. Pp. 517-522.
5. Caisso J.P., Cerny E., Rumin N.C. A Recursive Technique for Computing Delays in Series-Parallel MOS Transistor Circuits // IEEE Trans, on CAD. 1991, v. 10, n. 5. Pp. 589-595.
6. Bryant R.E. Graph-Based Algorithms for Boolean Function Manipulation//IEEE Trans, on Computers. 1986, v. 35, n. 8. Pp. 677-691.
7. Bern J., Gergov J., Meinel C, Slobodova A. Boolean Manipulation with Free BDDs / Proc. of EDAC-94. Pp. 200-207.
8. Prasad S.C., Roy K. Circuit Optimization for Minimization of Power Consumption under Delay Constraint / Proc. of Int. Workshop on Low Power Design. 1994. P. 15-20.
9. Gavrilov S., Glebov A., Rusakov S., Blaauw D., Jones L., Vijayan G. Fast Power Loss Calculation for Digital Static CMOS Circuits / Proc. of ED&TC-97. Pp. 411-415.
10. Glebov A., Gavrilov S., Blaauw D., Vijayan G., Pullcla S., Moore S. Library-Less Synthesis for Static CMOS Circuits, submitted for ICCAD-97.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 10. 1997
Ключевые слова: Моделирование, BDD-представление, КМОП-схемы, последовательно-параллельные цепи, логический синтез, оптимизация, булевы функции, алгоритмы на графах.
Публикации с ключевыми словами: Моделирование, оптимизация, BDD-представление, КМОП-схемы, последовательно-параллельные цепи, логический синтез, булевы функции, алгоритмы на графах
Публикации со словами: Моделирование, оптимизация, BDD-представление, КМОП-схемы, последовательно-параллельные цепи, логический синтез, булевы функции, алгоритмы на графах
Смотри также:
- Математическая модель взаимодействия предприятий по производству продуктов питания молочной отрасли АПК РФ
- Разработка программной среды для моделирования и оптимизации складской политики двухэшелонных многопродуктовых цепей поставки
- Возможности применения параллельных методов вычисления в системе программирования на языке S-FLOGOL
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



