научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2012
DOI: 10.7463/0912.0470529
Россия, МГТУ им. Н.Э. Баумана
chernobrivchenko.k@gmail.com
Введение
Публикация продолжает работу [1], посвященную исследованию эффективности модифицированного нами алгоритма непрерывно взаимодействующей колонии муравьев CIAC (ContinuousInteractingAntColony) [2].
Муравьиные алгоритмы представляют собой новый класс алгоритмов оптимизации, инспирированных живой природой. В основу алгоритмов положено моделирование самоорганизации в муравьиной колонии, как многоагентной системе, в которой каждый агент (муравей) функционирует по очень простым правилам, но поведение системы в целом оказывается высоко рациональным. Муравьи в колонии образуют структуру, называемую гетерархией, которая, в отличии от иерархии, предполагает не вертикальные связи между агентами системы, а горизонтальные, когда все агенты равноправны между собой. В колонии муравьев имеет место плотная гетерархия, когда каждый из агентов системы может связываться с любым другим агентом и в любой момент времени. Общение между муравьями происходит через каналы прямого взаимодействия и стигмергии (stigmergy). Прямое взаимодействие между агентами осуществляется посредством обмена пищей и выделениями желез (трофоллаксис). Канал стигмергии (следовой канал) представляет собой способ обмен информацией через феромонный след, оставляемый муравьями.
Муравьиные алгоритмы используют для решения задач, как дискретной, так и непрерывной оптимизации. Первым вариантом алгоритма колонии муравьев, разработанным для решения задачи непрерывной оптимизации, стал алгоритм непрерывной оптимизации колонией муравьев (ContinuousAntColonyOptimization, CACO), наметки которого были предложены Билчевым (G.Bilchev) и Парми (I.C. Parmee) в 1995 г. В настоящее время известно большое число алгоритмов непрерывной оптимизации колонией муравьев, одним из которых является упомянутый выше алгоритм CIAC. Для повышения эффективности алгоритма CIAC его авторы разработали модификацию HybridCIAC (HCIAC) [3], основной особенностью которой является реализация локального поиска с помощью широко известного алгоритма Нелдера-Мида.
В данной работе мы предлагаем модификацию алгоритма HCIAC на основе меметических (memetic) алгоритмов, которые представляют собой гибридные популяционные метаэвристические алгоритмы поисковой оптимизации, основанные на концепции мема и нео-дарвиновском принципе эволюции [4]. Модифицированный алгоритм назван нами HCIAC-M.
В контексте меметических алгоритмов мем является реализацией какого-либо алгоритма локальной оптимизации, уточняющего текущие решения на каждой итерации, либо через некоторое число итераций. В широком смысле, меметические алгоритмы можно рассматривать как гибридизацию одного из популяционных алгоритмов глобального поиска и одного или нескольких классических или популяционных алгоритмов локальной оптимизации.
Из различных вариантов меметических алгоритмов чаще всего используют вариант мультимемных (multi-memes) адаптивных алгоритмов. Основной задачей конструирования таких алгоритмов является выбор целесообразной стратегии использования того или иного мема из роя доступных мемов. Задача относится к классу задач метаоптимизации [5]. Указанную стратегию иногда называют гиперэвристикой (hyperheuristic).
Наиболее известны три следующие категории гиперэвристик, используемых в гиперэвристических адаптивных мультимемных алгоритмах: случайные (random) гиперэвристики, жадные (greedy) гиперэвристики, гиперэвристики cфункцией выбора (choice-function). В алгоритме HCIAC-Mиспользован один из вариантов жадной гиперэвристики.
HCIAC-Mвключает в себя еще одну модификацию алгоритма HCIAC– последний алгоритм дополнен процедурой встряски популяции, которая призвана диверсифицировать поиск и тем самым повысить вероятность локализации глобального экстремума целевой функции.
В пункте 1 приведена постановка задачи и представлены схемы алгоритмов CIAC и HCIAC. Предлагаемая модификация алгоритма HCIAC рассматривается в пункте 2. Пункт 3 посвящен исследованию эффективности алгоритма HCIAC-Mпри поиске глобального экстремума одноэкстремальной овражной функции Розенброка (Rosenbrock) и многоэкстремальной функции Растригина (Rastrigin) из известного пакета тестовых функций CES (CongressofEvolutionaryComputing) [6]. Последовательно представлены результаты исследования модифицированных встряской алгоритмов CIACи HCIAC, а также алгоритма HCIAC-M. В пункте 4 в качестве примера применения алгоритма HCIAC-Mрассмотрена практически значимая задача оптимизации системы двигатель-генератор [7], сводящаяся к задаче оптимального управления, которую мы решаем путем редукции к задаче нелинейного программирования, а затем к задаче безусловной оптимизации.
1. Постановка задачи и схема базового муравьиного алгоритма
Рассматриваем задачу многомерной глобальной безусловной оптимизации: найти максимум целевой функции ![]() , определенной на множестве D евклидова пространства
, определенной на множестве D евклидова пространства ![]() :
:
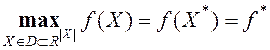 . (1)
. (1)
Здесь ![]() - вектор варьируемых параметров,
- вектор варьируемых параметров,
![]() ‑ (2)
‑ (2)
параллелепипед допустимых значений этого вектора.
Как мы отмечали выше, алгоритм HCIAC построен на основе алгоритма CIAC. Рассмотрим поэтому прежде последний алгоритм [2].
1.1. Алгоритм CIAC
Схема алгоритма CIACимеет следующий вид.
1) Создаем агентов (муравьев) ![]() ,
, ![]() и случайным образом распределяем их в области поиска D. Здесь
и случайным образом распределяем их в области поиска D. Здесь ![]() ‑ число агентов в колонии
‑ число агентов в колонии ![]() .
.
2) Моделируем работу канала стигмергии, для чего для каждого из агентов ![]() вычисляем координаты центра тяжести феромонных точек
вычисляем координаты центра тяжести феромонных точек
 ,
,
где ![]() - вектор координат i-ой феромонной точки,
- вектор координат i-ой феромонной точки, ![]() ‑ их общее число,
‑ их общее число,
 ‑
‑
нормированный интерес j-го агента к i-ой феромонной точке;
 .
.
Здесь ![]() - среднее расстояние между двумя агентами в колонии,
- среднее расстояние между двумя агентами в колонии, ![]() - количество феромона в точке
- количество феромона в точке ![]() ,
, ![]() - расстояние между j-м агентом и i-ой феромонной точкой.
- расстояние между j-м агентом и i-ой феромонной точкой.
3) Перемещаем агента ![]() в направлении точки
в направлении точки ![]() на случайное расстояние в пределах его размерного параметра
на случайное расстояние в пределах его размерного параметра 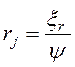 , где
, где ![]() – случайная величина, распределенная по нормальному закону с нулевым математическим ожиданием и среднеквадратичным отклонением
– случайная величина, распределенная по нормальному закону с нулевым математическим ожиданием и среднеквадратичным отклонением ![]() ;
; ![]() - делитель размерного параметра, определяющий величину этого перемещения.
- делитель размерного параметра, определяющий величину этого перемещения.
4) Моделируем функционирование канала прямого взаимодействия – агент ![]() читает из своей памяти случайное сообщение, полученное от агента
читает из своей памяти случайное сообщение, полученное от агента ![]() .
.
5) Сравниваем значение целевой функции ![]() в точке расположения агента
в точке расположения агента ![]() с соответствующим значением
с соответствующим значением ![]() , полученным в сообщении от агента
, полученным в сообщении от агента ![]() . Если
. Если ![]() , то агента
, то агента ![]() перемещаем в случайную точку гиперсферы, центром которой является точка
перемещаем в случайную точку гиперсферы, центром которой является точка ![]() , а радиусом - размерный параметр
, а радиусом - размерный параметр ![]() этого агента.
этого агента.
6) Если ![]() , то агент
, то агент ![]() посылает сообщение со своими координатами
посылает сообщение со своими координатами ![]() и значением целевой функции
и значением целевой функции ![]() случайному агенту популяции, а затем в пределах своего размерного параметра
случайному агенту популяции, а затем в пределах своего размерного параметра ![]() совершает случайное перемещение в окрестности точки
совершает случайное перемещение в окрестности точки ![]() .
.
7) После того, как по рассмотренной схеме все агенты колонии завершили свои перемещения, моделируем испарение феромонных точек (см. ниже).
8) Проверяем выполнение критерия останова, в качестве которого может использоваться условие достижения заданного числа итераций ![]() или условие стагнации вычислительного процесса
или условие стагнации вычислительного процесса
![]() ,
,
где ![]() ‑ заданное число итераций,
‑ заданное число итераций, ![]() ‑ малая положительная величина.
‑ малая положительная величина.
В каждой точке ![]() , в которой побывал муравей
, в которой побывал муравей ![]() , он оставляет феромонную точку
, он оставляет феромонную точку ![]() , интенсивность которой (количество феромона) на данной итерации tравна
, интенсивность которой (количество феромона) на данной итерации tравна ![]() , где
, где ![]() - номер итерации, на которой оставлена эта точка. Количество феромона в феромонных точках с ростом числа итераций уменьшается (феромон испаряется) в соответствии с рекуррентной формулой
- номер итерации, на которой оставлена эта точка. Количество феромона в феромонных точках с ростом числа итераций уменьшается (феромон испаряется) в соответствии с рекуррентной формулой
 (3)
(3)
где ![]() – коэффициент устойчивости феромонных точек. Формула означает, что феромонная точка исчезает, если количество феромона в ней становится равным величине
– коэффициент устойчивости феромонных точек. Формула означает, что феромонная точка исчезает, если количество феромона в ней становится равным величине ![]() . Начальное количество феромона агента
. Начальное количество феромона агента ![]() полагаем равным единице, а остальных агентов – пропорциональным соответствующим значениям целевой функции.
полагаем равным единице, а остальных агентов – пропорциональным соответствующим значениям целевой функции.
Размер памяти агента ограничен, так что максимально допустимое число сообщений в памяти каждого из агентов не превышает величины ![]() . В ситуации, когда возможно переполнение памяти (агент получает новое сообщение при текущем числе сообщений в его памяти, равном
. В ситуации, когда возможно переполнение памяти (агент получает новое сообщение при текущем числе сообщений в его памяти, равном ![]() ), одно из выбранных случайным образом сообщений удаляем из памяти, а новое сообщение записываем в нее.
), одно из выбранных случайным образом сообщений удаляем из памяти, а новое сообщение записываем в нее.
1.2. Алгоритм HCIAC
Алгоритм HCIAC использует следующие модификации алгоритма CIAC [3]. Во-первых, как мы отмечали выше, HCIAC реализует локальный поиск на основе алгоритма Нелдера-Мида. Во-вторых, HCIAC использует модифицированную модель канала стигмергии.
В алгоритме CIACв случае медленного испарения феромонных точек число этих точек может стать чрезвычайно большим, что приведет к значительному увеличению требуемой памяти ЭВМ и высоким вычислительным затратам. В алгоритме HCIAC для решения этой проблемы муравьи могут не только добавлять новые точки, но и усиливать старые, находящиеся в зоне видимости (visiblezone) агентов.
Схему алгоритма HCIAC передает следующая последовательность его основных шагов.
1) Инициализируем агентов по схеме алгоритма CIAC. Кроме того задаем начальные радиусы зон видимости ![]() , подчиненные нормальному закону распределения с математическим ожиданием и среднеквадратичным отклонением равными соответственно
, подчиненные нормальному закону распределения с математическим ожиданием и среднеквадратичным отклонением равными соответственно ![]() .
.
2) Моделируем испарение феромонных точек по формуле (3).
3) Для каждого из агентов ![]() реализуем этап глобального поиска.
реализуем этап глобального поиска.
3.1) Моделируем выбор агентом ![]() канала стигмергии или канала прямого взаимодействия на основании функции выбора (stimulus-responsefunction) вида
канала стигмергии или канала прямого взаимодействия на основании функции выбора (stimulus-responsefunction) вида
 , (4)
, (4)
где ![]() ‑ вероятность выбора канала стигмергии,
‑ вероятность выбора канала стигмергии, ![]() – привлекательность (stimulus) канала;
– привлекательность (stimulus) канала; ![]() ,
, ![]() ‑ одинаковые для всех агентов коэффициент гладкости (smoothness) и величина порога чувствительности (threshold) соответственно.
‑ одинаковые для всех агентов коэффициент гладкости (smoothness) и величина порога чувствительности (threshold) соответственно.
3.2) Если для агента ![]() был выбрал канал стигмергии, то отыскиваем все феромонные точки в пределах его зоны видимости
был выбрал канал стигмергии, то отыскиваем все феромонные точки в пределах его зоны видимости ![]() и по схеме алгоритма CIAC реализуем движение агента в направлении их центра тяжести.
и по схеме алгоритма CIAC реализуем движение агента в направлении их центра тяжести.
3.3) Если для агента ![]() выбрал канал прямого взаимодействия, то извлекаем из памяти этого агента первое сообщение и обрабатываем его в соответствии с алгоритмом CIAC.
выбрал канал прямого взаимодействия, то извлекаем из памяти этого агента первое сообщение и обрабатываем его в соответствии с алгоритмом CIAC.
4) Если в зоне видимости агента ![]() нет феромонных точек (случай 3.2) или в его памяти нет сообщений (случай 3.3), то основываясь на мотивации (motivation) агента
нет феромонных точек (случай 3.2) или в его памяти нет сообщений (случай 3.3), то основываясь на мотивации (motivation) агента ![]() по формуле вида (4) производим выбор в пользу работы агента
по формуле вида (4) производим выбор в пользу работы агента ![]() с каналом прямого взаимодействия или в пользу локального поиска. Здесь величина
с каналом прямого взаимодействия или в пользу локального поиска. Здесь величина ![]() в отличие от привлекательности
в отличие от привлекательности ![]() , является динамической величиной cнулевым начальным значением.
, является динамической величиной cнулевым начальным значением.
4.1) Если выбор сделан в пользу работы агента ![]() с каналом прямого взаимодействия, то моделируем отправку этим агентом сообщения случайному агенту популяции и полагаем
с каналом прямого взаимодействия, то моделируем отправку этим агентом сообщения случайному агенту популяции и полагаем ![]() , то есть, увеличиваем мотивацию агента на небольшую величину
, то есть, увеличиваем мотивацию агента на небольшую величину ![]() .
.
4.2) В случае выбора второго варианта действий, исходя из текущего положения агента ![]() , полагаем мотивацию
, полагаем мотивацию ![]() равной нулю и выполняем следующие действия.
равной нулю и выполняем следующие действия.
4.2.1) Запускаем локальный поиск алгоритмом Нелдера-Мида, полагая начальную длину ребра симплекса, равной текущему радиусу зоны видимости ![]() . Локальный поиск ограничиваем
. Локальный поиск ограничиваем ![]() оценками значений целевой функции. В качестве конечного положения агента
оценками значений целевой функции. В качестве конечного положения агента ![]() принимаем положение, соответствующее лучшему достигнутому значению функции
принимаем положение, соответствующее лучшему достигнутому значению функции ![]() .
.
4.2.2) Отыскиваем видимые данным агентом феромонные точки.
4.2.3) . Если указанные точки имеются, усиливаем ближайшую из них ![]() в соответствии с формулой
в соответствии с формулой
 ,
,
а радиус видимости ![]() уменьшаем до величины, равной расстоянию данного агента до наиболее дальней феромонной точки в зоне его видимости.
уменьшаем до величины, равной расстоянию данного агента до наиболее дальней феромонной точки в зоне его видимости.
4.2.4) Если указанные феромонные точки отсутствуют, формируем новую феромонную точку ![]() с количеством феромона, пропорциональным
с количеством феромона, пропорциональным ![]() . Мотивацию
. Мотивацию ![]() устанавливаем равной нулю.
устанавливаем равной нулю.
5) Реализуем случайное перемещение агента ![]() в пределах его текущей зоны видимости
в пределах его текущей зоны видимости ![]() .
.
6) По правилам алгоритма CIACпродолжаем либо завершаем итерации.
2. Модификация базового алгоритма
Результаты исследований, выполненных авторами алгоритма HCIAC, показывают, что этот алгоритм по сравнению с алгоритмом CIAC позволяет значительно повысить скорость сходимости итераций. Однако ценой этого является значительное увеличение числа испытаний (вычислений значений целевой функции). Так, в наших экспериментах показано, что один акт локального поиска пятимерной функции Розенброка может требовать до 800 испытаний. Причиной этого является низкая скорость сходимости алгоритма Нелдера-Мида на некоторых классах функций. При решении практически значимых задач оптимизации, в которых целевая функция имеет высокую вычислительную сложность, данное обстоятельство может привести к недопустимо большим вычислительным затратам.
В алгоритме HCIAC-Mв качестве мемов используем алгоритм ![]() Нелдера-Мида, алгоритм
Нелдера-Мида, алгоритм ![]() ортогонального исследования области поиска [8], квазиньютоновский алгоритм
ортогонального исследования области поиска [8], квазиньютоновский алгоритм ![]() со смешанной процедурой квадратичного и кубического поиска [9]. Таким образом, рой мемов состоит из мемов
со смешанной процедурой квадратичного и кубического поиска [9]. Таким образом, рой мемов состоит из мемов ![]() и число мемов
и число мемов ![]() .
.
Используем жадную гиперэвристику, основные особенности которой заключаются в следующем.
1) Лучшего для данного агента ![]() мема выбираем на основе
мема выбираем на основе ![]() запусков локального поиска.
запусков локального поиска.
2) Критерий эффективности мема ![]() строим на основе среднего числа испытаний за один запуск алгоритма локального поиска
строим на основе среднего числа испытаний за один запуск алгоритма локального поиска
 ,
, ![]() ,
,
где ![]() ‑ число испытаний в процессе
‑ число испытаний в процессе ![]() -го локального поиска мемом
-го локального поиска мемом ![]() . Точнее говоря, мема
. Точнее говоря, мема ![]() объявляем победителем, если
объявляем победителем, если
![]()
и если лучшее решение ![]() , полученное им, не более чем на величину
, полученное им, не более чем на величину ![]() меньше лучшего решения
меньше лучшего решения ![]() , найденного популяцией мемов, то есть
, найденного популяцией мемов, то есть
![]() .
.
3) На последних ![]() итерациях мема-победителя выбираем только по второму из указанных критериев, то есть полагаем, что
итерациях мема-победителя выбираем только по второму из указанных критериев, то есть полагаем, что
![]() .
.
Как отмечалось выше, алгоритм HCIAC-Mвключает в себя еще процедуру встряски популяции, которая запускается c шагом
![]() ,
,
где ![]() ‑ текущий номер итерации;
‑ текущий номер итерации; ![]() ‑ свободные параметры алгоритма. В соответствии с этой формулой с ростом числа итераций шаг встряски
‑ свободные параметры алгоритма. В соответствии с этой формулой с ростом числа итераций шаг встряски ![]() увеличивается, обеспечивая переход от исследования пространства поиска к точной локализации найденного максимума целевой функции.
увеличивается, обеспечивая переход от исследования пространства поиска к точной локализации найденного максимума целевой функции.
Суть процедуры встряски популяции заключается в следующем.
1) После завершения очередных ![]() итераций отбираем
итераций отбираем ![]() не лучших агентов
не лучших агентов ![]() с координатами
с координатами ![]() и распределяем их случайным образом в области поиска в точках
и распределяем их случайным образом в области поиска в точках ![]() соответственно;
соответственно; ![]() ,
, ![]() .
.
2) Вычисляем значения целевой функции в точках ![]() и создаем в этих точках феромонные пятна, интенсивность которых полагаем равной
и создаем в этих точках феромонные пятна, интенсивность которых полагаем равной
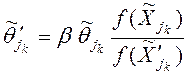 , (5)
, (5)
где ![]() ‑ количество феромона в точке
‑ количество феромона в точке ![]() ,
, ![]() ‑ свободный параметр.
‑ свободный параметр.
3. Исследование эффективности алгоритма HCIAC-M
Модификация алгоритма HCIAC была выполнена в несколько этапов. Соответственно многоэтапным было исследование его эффективности.
Реализация рассматриваемых алгоритмов выполнена среде MatLab Вычислительные эксперименты проводились на персональном компьютере с процессором IntelCore 2 DuoT8100 2,1 ГГц и оперативной памятью объемом 2 ГБ.
3.1. Модификация алгоритма CIACвстряской.
В качестве тестовой использована пятимерная функция Растригина. Если не указано иное, вычислительные эксперименты выполнены со значениями свободных параметров модифицированного алгоритма CIAC, называемого нами CIAC-S, которые использованы в работе [1]: коэффициент устойчивости феромонных точек ![]() ; минимальное количество феромона
; минимальное количество феромона ![]() ; среднеквадратичное отклонение размерного параметра
; среднеквадратичное отклонение размерного параметра![]() ; число агентов в колонии
; число агентов в колонии ![]() ; делитель размерного параметра
; делитель размерного параметра ![]() ; максимально допустимое число итераций
; максимально допустимое число итераций ![]() ; период стагнации
; период стагнации ![]() . Число стартов алгоритма принято равным 30;
. Число стартов алгоритма принято равным 30; ![]() ;
; ![]() ;
; ![]() . Относительное число агентов, подвергшихся перемещению в процессе встряски популяции, равно
. Относительное число агентов, подвергшихся перемещению в процессе встряски популяции, равно 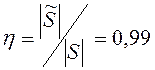 .
.
В качестве критерия эффективности алгоритма используем величину ![]() ‑ оценку вероятности локализации глобального максимума функции. Данная оценка во всех случаях получена по итогам мультистарта как процент успешных стартов, то есть стартов, в результате которых глобальный максимум найден с требуемой точностью.
‑ оценку вероятности локализации глобального максимума функции. Данная оценка во всех случаях получена по итогам мультистарта как процент успешных стартов, то есть стартов, в результате которых глобальный максимум найден с требуемой точностью.
Рисунок 1 иллюстрирует вероятность ![]() в функции величины делителя размерного параметра
в функции величины делителя размерного параметра ![]() . Из сравнения этого рисунка с рисунком 13 публикации [1] вытекает, что встряска обеспечивает значительное повышение вероятности локализации глобального экстремума. Так, при
. Из сравнения этого рисунка с рисунком 13 публикации [1] вытекает, что встряска обеспечивает значительное повышение вероятности локализации глобального экстремума. Так, при ![]() алгоритм CIAC-S обеспечивает
алгоритм CIAC-S обеспечивает ![]() , в то время как исходный алгоритм – всего
, в то время как исходный алгоритм – всего ![]() . В дальнейших экспериментах принято
. В дальнейших экспериментах принято ![]() .
.

Рисунок 1 – Оценка вероятности ![]() в функции значений параметра
в функции значений параметра ![]() : пятимерная функция Растригина; алгоритм CIAC-S
: пятимерная функция Растригина; алгоритм CIAC-S
Зависимость вероятности ![]() от значений параметра
от значений параметра ![]() , отвечающего за частоту запуска процедуры встряски, показывает рисунок 2.
, отвечающего за частоту запуска процедуры встряски, показывает рисунок 2.

Рисунок 2 – Оценка вероятности ![]() в функции значений параметра
в функции значений параметра ![]() : пятимерная функция Растригина; алгоритм CIAC-S
: пятимерная функция Растригина; алгоритм CIAC-S
Из рисунка 2 следует, что, как и ожидалось, малые значения величины ![]() , которым соответствует высокая частота встряски, приводят к более высокой вероятности локализации глобального экстремума. Ценой этого является увеличение числа испытаний и, как следствие, времени решения задачи. Поэтому для дальнейших исследований принимаем компромиссное значение параметра
, которым соответствует высокая частота встряски, приводят к более высокой вероятности локализации глобального экстремума. Ценой этого является увеличение числа испытаний и, как следствие, времени решения задачи. Поэтому для дальнейших исследований принимаем компромиссное значение параметра ![]() , равное
, равное ![]() .
.
Результаты исследования зависимости ![]() иллюстрирует рисунок 3. Заметим, что, как следует из формулы (5), большим значениям величины
иллюстрирует рисунок 3. Заметим, что, как следует из формулы (5), большим значениям величины ![]() соответствует большее количество феромона, откладываемого в новых точках, то есть в точках, возникших в результате реализации процедуры встряски.
соответствует большее количество феромона, откладываемого в новых точках, то есть в точках, возникших в результате реализации процедуры встряски.
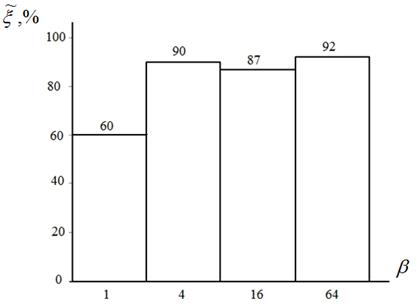
Рисунок 3 – Оценка вероятности ![]() в функции значений параметра
в функции значений параметра ![]() : пятимерная функция Растригина; алгоритм CIAC-S
: пятимерная функция Растригина; алгоритм CIAC-S
Рисунок 3 показывает, что увеличение значений параметра ![]() ожидаемо повышает вероятность локализации экстремума. Однако при этот значительно возрастает число испытаний, поскольку из-за большего количества феромона в новых точках он в этих точках испаряется медленнее. На основе данного исследования для многоэкстремальных функций типа функции Растригина можно рекомендовать значение
ожидаемо повышает вероятность локализации экстремума. Однако при этот значительно возрастает число испытаний, поскольку из-за большего количества феромона в новых точках он в этих точках испаряется медленнее. На основе данного исследования для многоэкстремальных функций типа функции Растригина можно рекомендовать значение ![]() , которое мы используем в последующих экспериментах.
, которое мы используем в последующих экспериментах.
Результаты варьирования относительного числа агентов ![]() , участвующих в процедуре встряски, иллюстрирует рисунок 4.
, участвующих в процедуре встряски, иллюстрирует рисунок 4.
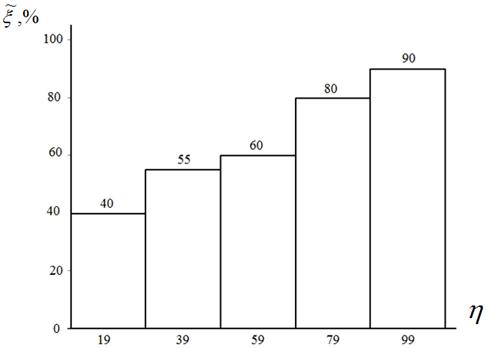
Рисунок 4 – Оценка вероятности ![]() в функции значений параметра
в функции значений параметра ![]() : пятимерная функция Растригина; алгоритм CIAC-S
: пятимерная функция Растригина; алгоритм CIAC-S
Из рисунка 4 отчетливо видно, что встряска популяции повышает вероятность локализации глобального экстремума в тем большей степени, чем выше значение этого параметра. Однако с ростом величины ![]() быстро растет требуемое число испытаний, так что в качестве оптимального значения этой величины мы рекомендуем значение
быстро растет требуемое число испытаний, так что в качестве оптимального значения этой величины мы рекомендуем значение ![]() , используемое в дальнейших вычислительных экспериментах.
, используемое в дальнейших вычислительных экспериментах.
Таким образом, представленные результаты показывают эффективность предложенной модификации алгоритма CIAC. Исследование позволило определить оптимальные для пятимерной функции Растригина значения свободных параметров процедуры встряски. Есть основания полагать, что эти значения будут близки к оптимальным и для других многоэкстремальных функций. Важно, что процедура встряски не уменьшает результирующую точность алгоритма, поскольку на его завершающих итерациях эта процедура «отключается». Процедура оставляет широкие возможности оптимизации ее свободных параметров по критериям вероятности локализации глобального экстремума и вычислительной сложности.
3.2. Модификация алгоритма HCIACвстряской
Исследование эффективности данной модификации алгоритма HCIAC, названной нами HCIAC-S, выполнено на функциях Розенброка и Растригина. В качестве значений свободных параметров алгоритма использованы значения, указанные в п. 3.1.
Зона видимости агента в алгоритме HCIACдинамически меняется в процессе поиска, поэтому исследование зависимости ![]() в данном случае не имеет смысла. В качестве основного варьируемого параметра рассматриваем число агентов
в данном случае не имеет смысла. В качестве основного варьируемого параметра рассматриваем число агентов ![]() в популяции.
в популяции.
Исследование выполнено для пяти- и десятимерной функций Розенброка. В работе [3] показано, что при поиске экстремума этой функции с помощью канонического алгоритмаHCIAC, возникает ряд проблем. Модификация алгоритма HCIACвстряской имела целью, как отмечалось выше, повышение эффективности алгоритма при поиске экстремума многоэкстремальных функций. Использование в качестве тестовых функций Розенброка разной размерности позволяет проверить насколько процедура встряски эффективна для иного класса функций – класса овражных функций.
Результаты исследования для пятимерной функции Розенброка иллюстрирует рисунок 5, а для десятимерной функции – рисунок 6.

Рисунок 5 – Оценка вероятности ![]() в функции размера популяции
в функции размера популяции ![]() : пятимерная функция Розенброка; алгоритм HCIAC-S
: пятимерная функция Розенброка; алгоритм HCIAC-S

Рисунок 6 – Оценка вероятности ![]() в функции размера популяции
в функции размера популяции ![]() : десятимерная функция Розенброка; алгоритм HCIAC-S
: десятимерная функция Розенброка; алгоритм HCIAC-S
Рисунок 5 показывает, что популяция уже из 100 агентов обеспечивает практически стопроцентную вероятность локализации экстремума пятимерной функции Розенброка. Поскольку увеличение числа агентов популяции вызывает почти пропорциональный рост требуемого числа испытаний (в рассматриваемом примере с ![]() испытаний при
испытаний при ![]() до
до ![]() при
при ![]() ), такое поведение величины
), такое поведение величины ![]() является важным с точки зрения сокращения вычислительных затрат. Аналогичные выводы можно сделать из рисунка 6 для десятимерной функции Розенброка. Заметим, что в тех же условиях для обеспечения 100 % вероятности локализации экстремума алгоритм CIACтребовал число агентов в популяции, равное
является важным с точки зрения сокращения вычислительных затрат. Аналогичные выводы можно сделать из рисунка 6 для десятимерной функции Розенброка. Заметим, что в тех же условиях для обеспечения 100 % вероятности локализации экстремума алгоритм CIACтребовал число агентов в популяции, равное ![]() [1].
[1].
Отметим следующее обстоятельство. Благодаря динамическому изменению зоны видимости агента и гибридизации с алгоритмом локального поиска, алгоритм HCIAC-S в обоих экспериментах обеспечил среднюю абсолютную погрешность порядка 10-8 ‑ 10-9, что на порядок меньше лучшего результата алгоритма CIAC.
Некоторые результаты исследования эффективности алгоритмаHCIAC-Sдля функции Растригина представлены на рисунке 7.
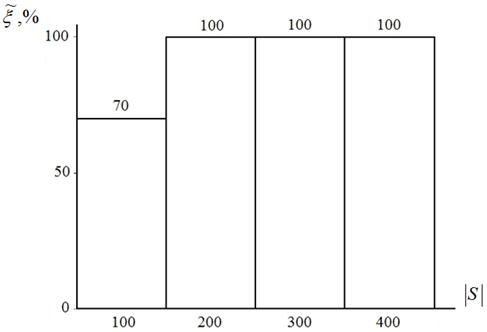
Рисунок 7 – Оценка вероятности ![]() в функции размера популяции
в функции размера популяции ![]() : пятимерная функция Розенброка; алгоритм HCIAC-S
: пятимерная функция Розенброка; алгоритм HCIAC-S
Из рисунка 7 вытекает, что алгоритм HCIAC обеспечивает 100 % вероятность локализации глобального экстремума пятимерной функции Растригина уже при 200 агентах (против 398 агентов алгоритма CIAC[1]). Данное обстоятельство, как отмечалось выше, позволяет значительно уменьшить вычислительные затраты. Алгоритм обеспечил среднюю абсолютную погрешность решения порядка 10-7 ‑ 10-8, то есть на два-три порядка меньше, чем лучший результат алгоритма CIAC.
Итого, на основе представленных результатов можно сделать вывод, что гибридизация алгоритма CIAC с алгоритмом локального поиска Нелдера-Мида, а также использование процедуры встряски позволяют существенно повысить эффективность алгоритма, как по критерию вероятности локализации глобального экстремума, так и по критериям средней абсолютной погрешности решения и суммарных вычислительных затрат. При этом снижение вычислительных затрат имеет место, не смотря на то, что применение алгоритма Нелдера-Мида в локальном поиске неизбежно влечет за собой увеличение суммарного числа испытаний, необходимых для эволюции каждого из агентов в течение одной итерации. Эффект обусловлен следующими причинами: возможность использования меньшего числа агентов для обеспечения той же точности поиска; уменьшение общего числа феромонных точек в зоне поиска; более высокая скорость сходимости алгоритма.
3.3. Мультимемеевая модификация алгоритма HCIAC
Эффективность алгоритма HCIAC-Mисследуем на пятимерных тестовых функциях Розенброка и Растригина. Мультимемеевую модификацию в экспериментах, результаты которых представлены ниже, определяют следующие значения свободных параметров: число запусков локального поиска ![]() , точность решения
, точность решения ![]() , число последних итераций
, число последних итераций ![]() . Остальные свободные параметры алгоритма HCIAC-Mимеют значения, указанные в пп. 3.1, 3.2.
. Остальные свободные параметры алгоритма HCIAC-Mимеют значения, указанные в пп. 3.1, 3.2.
Эффективность рассматриваемых мемов для функций Розенброка и Растригина иллюстрируют рисунки 8, 9 соответственно, на которых величина ![]() представляет собой оценку вероятности использования мема
представляет собой оценку вероятности использования мема ![]() . Напомним, что мему
. Напомним, что мему ![]() соответствует алгоритм Нелдера-Мида, мему
соответствует алгоритм Нелдера-Мида, мему ![]() ‑ алгоритм ортогонального исследования области поиска, мему
‑ алгоритм ортогонального исследования области поиска, мему ![]() ‑ квазиньютоновский алгоритм со смешанной процедурой квадратичного и кубического поиска (п. 2).
‑ квазиньютоновский алгоритм со смешанной процедурой квадратичного и кубического поиска (п. 2).

Рисунок 8 – Оценка вероятность использования мемов: функция Розенброка (![]() ); алгоритм HCIAC-M
); алгоритм HCIAC-M

Рисунок 9 – Оценка вероятность использования мемов: функция Растригина (![]() ); алгоритм HCIAC-M
); алгоритм HCIAC-M
Рисунки 8, 9 получены при использовании в качестве меры эффективности мемов среднего числа испытаний ![]() за один запуск алгоритма локального поиска. Рисунки показывают, что в 86 % и 79 % случаев для функции Розенброка и Растригина соответственно, лучший результат показал квазиньютоновский алгоритм. Аналогично в 14 % и в 21 % случаев лучшие результаты продемонстрировал алгоритм Нелдера-Мида. Алгоритм ортогонального поиска по данному критерию не смог составить конкуренцию квазиньютоновскому алгоритму и алгоритму Нелдера-Мида. Отметим слабую чувствительность представленных результатов к классу экстремизируемой функции.
за один запуск алгоритма локального поиска. Рисунки показывают, что в 86 % и 79 % случаев для функции Розенброка и Растригина соответственно, лучший результат показал квазиньютоновский алгоритм. Аналогично в 14 % и в 21 % случаев лучшие результаты продемонстрировал алгоритм Нелдера-Мида. Алгоритм ортогонального поиска по данному критерию не смог составить конкуренцию квазиньютоновскому алгоритму и алгоритму Нелдера-Мида. Отметим слабую чувствительность представленных результатов к классу экстремизируемой функции.
На рисунках 10, 11 представлены средние по числу запусков локального поиска погрешности ![]() мемов
мемов ![]() . Аналогичные результаты для ортогонального алгоритма не приведены, поскольку его эффективность по данному критерию оказалась не порядок ниже.
. Аналогичные результаты для ортогонального алгоритма не приведены, поскольку его эффективность по данному критерию оказалась не порядок ниже.
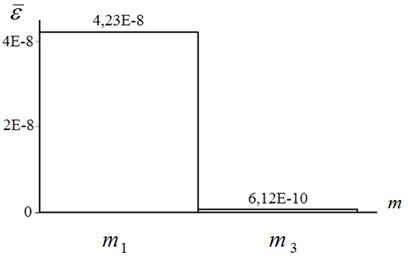
Рисунок 10 – Средняя погрешность локального поиска мемами ![]() : функция Розенброка (
: функция Розенброка (![]() ); алгоритм HCIAC-M
); алгоритм HCIAC-M

Рисунок 11 – Средняя погрешность локального поиска мемами ![]() : функция Растригина (
: функция Растригина (![]() ); алгоритм HCIAC-M
); алгоритм HCIAC-M
Из рисунков 10, 11 следует, что средняя точность квазиньютоновского алгоритма примерно на два порядка выше такой же точности алгоритма Нелдера-Мида.
Средние числа испытаний ![]() за один запуск алгоритма локального поиска для мемов
за один запуск алгоритма локального поиска для мемов ![]() иллюстрируют рисунки 12, 13.
иллюстрируют рисунки 12, 13.

Рисунок 12 – Средняя число испытаний за один запуск алгоритма локального поиска для мемов ![]() : функция Розенброка (
: функция Розенброка (![]() );
);
алгоритм HCIAC-M
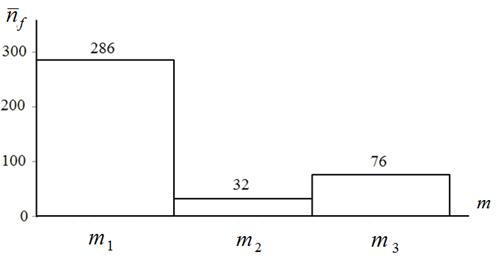
Рисунок 13 – Средняя число испытаний за один запуск алгоритма локального поиска для мемов ![]() : функция Растригина (
: функция Растригина (![]() );
);
алгоритм HCIAC-M
Рисунки 12, 13 показывают, что по критерию ![]() в несколько раз лучшим является алгоритм ортогонального поиска. По этому же критерию преимущество квазиньютоновского алгоритма над алгоритмом Нелдера-Мида достигает почти четырех раз (для функции Растригина).
в несколько раз лучшим является алгоритм ортогонального поиска. По этому же критерию преимущество квазиньютоновского алгоритма над алгоритмом Нелдера-Мида достигает почти четырех раз (для функции Растригина).
Представленные результаты исследования свидетельствуют о том, что задачу выбора лучшего мема следует рассматривать как трех- или более критериальную задачу.
3.4. Сравнение эффективности алгоритмов CIAC, HCIACи HCIAC-M
Введем в рассмотрение еще один критерий эффективности алгоритма ‑ среднее по мультистарту число испытаний ![]() за время работы алгоритма. Значения этого критерия для функции Растригина (
за время работы алгоритма. Значения этого критерия для функции Растригина (![]() ) и алгоритмов CIAC, HCIACи HCIAC-Mпредставлены на рисунке 14. Использованы указанные выше значения свободных параметров алгоритмов. Число агентов в популяции
) и алгоритмов CIAC, HCIACи HCIAC-Mпредставлены на рисунке 14. Использованы указанные выше значения свободных параметров алгоритмов. Число агентов в популяции ![]() для алгоритма CIACпринято равным 398, а для алгоритмов HCIAC, HCIAC-M– равным 400.
для алгоритма CIACпринято равным 398, а для алгоритмов HCIAC, HCIAC-M– равным 400.

Рисунок 14 – Среднее по мультистарту число испытаний за все время решения задачи: функция Растригина (![]() ); алгоритмы CIAC, HCIAC, HCIAC-M
); алгоритмы CIAC, HCIAC, HCIAC-M
Из рисунка 14 вытекает, что алгоритм HCIAC-M обеспечивает почти тоже суммарное число испытаний, что алгоритм CIAC и почти в четыре раза меньшее число, чем алгоритм HCIAC. В целом, результаты данного исследования показывают, что алгоритм HCIAC-M позволяет для пятимерной функции Растригина примерно в четыре раза повысить быстродействие, сохранив практически прежней вероятность локализации глобального экстремума.
4.Пример
Рассматриваем силовую часть электрического привода типа генератор-двигатель, предназначенного для управления некоторым рабочим механизмом (рисунок 15) [7].

Рисунок 15 – Схема силовой части электрического привода типа генератор-двигатель: Г – генератор; Д – двигатель; РМ –рабочий механизм
Динамику системы описываем системой алгебро-дифференциальных уравнений вида
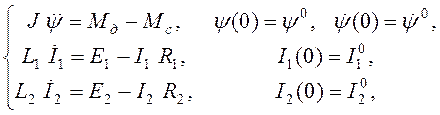 (6)
(6)
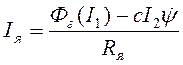 , (7)
, (7)
где приняты следующие обозначения: J — момент инерции якоря двигателя и приводимого им в движение рабочего механизма; ![]() — сопротивление якоря двигателя;
— сопротивление якоря двигателя; ![]() — угол поворота вала двигателя;
— угол поворота вала двигателя; ![]() — момент, развиваемый двигателем;
— момент, развиваемый двигателем; ![]() - момент нагрузки;
- момент нагрузки; ![]() ,
, ![]() ,
, ![]() ,
, ![]() – индуктивность обмотки возбуждения генератора, его омическое сопротивление, ток и электродвижущая сила (ЭДС) соответственно;
– индуктивность обмотки возбуждения генератора, его омическое сопротивление, ток и электродвижущая сила (ЭДС) соответственно; ![]() ,
, ![]() ,
, ![]() ,
, ![]() – аналогичные величины обмотки возбуждения двигателя;
– аналогичные величины обмотки возбуждения двигателя; ![]() - ЭДС в контуре якоря двигателя, связанная с током в его обмотке возбуждения выражением
- ЭДС в контуре якоря двигателя, связанная с током в его обмотке возбуждения выражением ![]() ;
; ![]() — ЭДС в контуре якоря двигателя, где
— ЭДС в контуре якоря двигателя, где ![]() – коэффициент пропорциональности.
– коэффициент пропорциональности.
Во-первых, при заданных начальных условиях требуется найти закон изменения во времени ЭДС ![]() , который минимизирует значение функционала
, который минимизирует значение функционала
 , (8)
, (8)
имеющего смысл суммарных затрат энергии на перемещение якоря двигателя за период времени ![]() .
.
Во-вторых, функция ![]() должна обеспечивать поворот якоря двигателя на требуемый угол
должна обеспечивать поворот якоря двигателя на требуемый угол ![]() за указанный период времени. Другими словами, эта функция должна обеспечивать минимальное значение функционала
за указанный период времени. Другими словами, эта функция должна обеспечивать минимальное значение функционала
![]() . (9)
. (9)
В-третьих, функция ![]() должна обеспечивать нулевую угловую скорости якоря двигателя в момент времени
должна обеспечивать нулевую угловую скорости якоря двигателя в момент времени ![]() , то есть минимизировать функционал
, то есть минимизировать функционал
![]() . (10)
. (10)
Таким образом, имеем трехкритериальную задачу оптимального управления: найти допустимое управление ![]() , которое на решениях системы уравнений (6), (7) обеспечивает минимум критериев оптимальности (8) - (10).
, которое на решениях системы уравнений (6), (7) обеспечивает минимум критериев оптимальности (8) - (10).
При всех известных недостатках решения задачи оптимального управления методом сведения ее к задаче нелинейного программирования, используем именно этот метод [10]. Обозначим для простоты записи ![]() и положим, что множество допустимых управлений
и положим, что множество допустимых управлений ![]() определяют двухсторонние ограничения вида
определяют двухсторонние ограничения вида ![]() . Покроем интервал
. Покроем интервал ![]() равномерной сеткой, узлы которой обозначим
равномерной сеткой, узлы которой обозначим ![]()
![]() . Будем искать оптимальное управление
. Будем искать оптимальное управление ![]() в классе кусочно-линейных функций (рисунок 16).
в классе кусочно-линейных функций (рисунок 16).
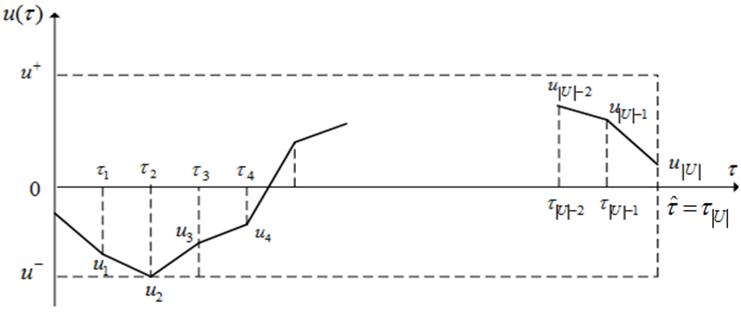
Рисунок 16 - Кусочно-линейная аппроксимация управления ![]()
Обозначив ![]() -
- ![]() -вектор, где
-вектор, где ![]() , получим трехкритериальную задачу вида
, получим трехкритериальную задачу вида
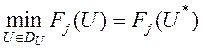 ,
, ![]() ; (11)
; (11)
![]() .
.
Переведем критерии оптимальности ![]() ,
, ![]() в ограничения с помощью алгоритма штрафных функций, то есть перейдем от задачи (11) к одноцелевой задаче глобальной безусловной оптимизации
в ограничения с помощью алгоритма штрафных функций, то есть перейдем от задачи (11) к одноцелевой задаче глобальной безусловной оптимизации
![]() , (12)
, (12)
где ![]() - коэффициенты штрафа.
- коэффициенты штрафа.
Примем следующие значения параметров задачи: J=0,425 кг·м2; ![]() =0,224 Ом;
=0,224 Ом; ![]() Нм, где
Нм, где ![]() ‑ масштабный коэффициент;
‑ масштабный коэффициент; ![]() =150 Н·м;
=150 Н·м; ![]() =8 Гн;
=8 Гн; ![]() =43 Ом;
=43 Ом; ![]() =8 Гн;
=8 Гн; ![]() =43 Ом;
=43 Ом; ![]() 40 В;
40 В; ![]() , где
, где ![]() – коэффициент кривой намагничивания; c=1;
– коэффициент кривой намагничивания; c=1; ![]() ;
; ![]() 100 В. Начальные условия примем нулевыми:
100 В. Начальные условия примем нулевыми: ![]() ;
; ![]() . Конечное состояние угла поворота якоря двигателя полагаем равным
. Конечное состояние угла поворота якоря двигателя полагаем равным ![]() . Движение системы рассматриваем на интервале
. Движение системы рассматриваем на интервале ![]() , то есть полагаем
, то есть полагаем ![]() с.
с.
Число узлов сетки, покрывающей интервал ![]() , принимаем равным 21, так что размерность вектора варьируемых параметров
, принимаем равным 21, так что размерность вектора варьируемых параметров ![]() . Потребуем удовлетворения ограничений
. Потребуем удовлетворения ограничений
![]() , (13)
, (13)
![]() (14)
(14)
с точностями ![]() ,
, ![]() соответственно. Начальные значения коэффициентов штрафа
соответственно. Начальные значения коэффициентов штрафа ![]() принимаем равными 2,0; 5,0.
принимаем равными 2,0; 5,0.
4.1. Алгоритм CIAC-S
Принимаем следующие значения основных свободных параметров алгоритма: размер популяции равен ![]() ; максимальное число поколений
; максимальное число поколений ![]() ; коэффициент устойчивости феромонных точек ρ=0,1; минимальное количество феромона в точке θmin=0,0001; максимальное число сообщений
; коэффициент устойчивости феромонных точек ρ=0,1; минимальное количество феромона в точке θmin=0,0001; максимальное число сообщений ![]() ; делитель размерного параметра для всех агентов одинаков и равен
; делитель размерного параметра для всех агентов одинаков и равен
![]() ,
,
где ![]() ‑ случайная величина, распределенная по нормальному закону с нулевым математическим ожиданием и средним квадратичным отклонением
‑ случайная величина, распределенная по нормальному закону с нулевым математическим ожиданием и средним квадратичным отклонением ![]() .
.
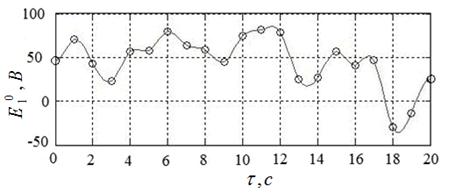
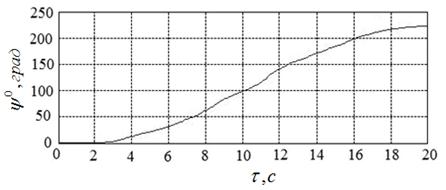
Пример начального приближения к решению иллюстрирует рисунок 17. Указанному приближению соответствуют угол ![]() , угловая скорость
, угловая скорость  и расход энергии
и расход энергии ![]() .
.
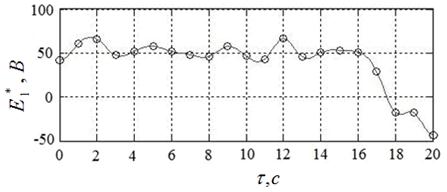
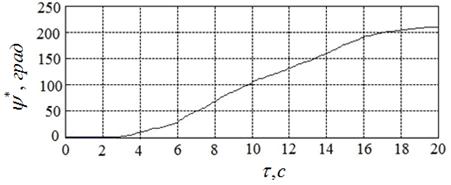
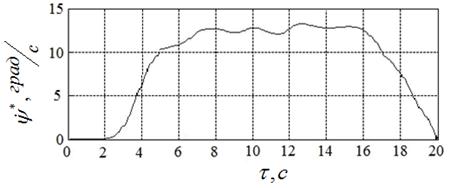
Лучшие (с точки зрения достигнутого значения функционала (8) результаты вычислительного эксперимента иллюстрируют рисунки 18а – 18в. Рисунок 18а показывает найденное оптимальное управление ![]() , а рисунки 18б, 18в – соответствующие законы изменения во времени угла поворота якоря двигателя
, а рисунки 18б, 18в – соответствующие законы изменения во времени угла поворота якоря двигателя ![]() и его скорости
и его скорости ![]() .
.
а) ![]()
б) ![]()
в) ![]()
Рисунок 17 – Пример начального приближения к решению ![]() и соответствующие функции
и соответствующие функции ![]() ,
, ![]() ;
; ![]()
а) ![]()
б) ![]()
в) ![]()
Рисунок 18 – Результаты решения задачи – оптимальная функция ![]() и соответствующие функции
и соответствующие функции ![]() ,
, ![]() ;
; ![]() ; алгоритм CIAC-S
; алгоритм CIAC-S
Полученному решению задачи соответствуют угол ![]() , угловая скорость
, угловая скорость  и расход энергии
и расход энергии ![]() . Таким образом, требование (13) выполнено с точностью 0,3
. Таким образом, требование (13) выполнено с точностью 0,3![]() , требование (14) – с точностью
, требование (14) – с точностью 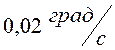 , а расход энергии уменьшился по сравнению с начальным приближением более чем на 40 %.
, а расход энергии уменьшился по сравнению с начальным приближением более чем на 40 %.
Рассмотрим также движение системы на интервале ![]() секунд, когда конечный угол поворота якоря двигателя равен
секунд, когда конечный угол поворота якоря двигателя равен ![]() м. Число узлов сетки, покрывающей интервал
м. Число узлов сетки, покрывающей интервал ![]() , принимаем равным 31, так что размерность вектора варьируемых параметров
, принимаем равным 31, так что размерность вектора варьируемых параметров ![]() .
.
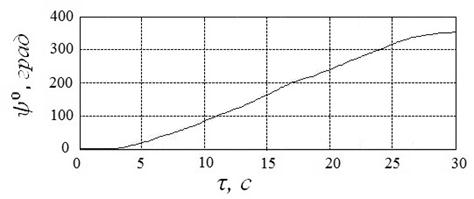
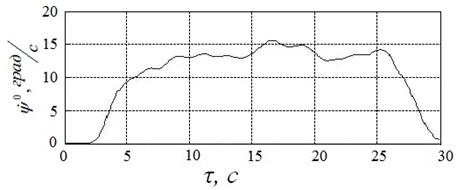
Пример начального приближения к решению в этом случае иллюстрирует рисунок 19. Указанному приближению соответствуют угол ![]() , угловая скорость
, угловая скорость 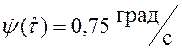 и расход энергии
и расход энергии ![]() .
.

а) ![]()
б) ![]()
в) ![]()
Рисунок 19 – Пример начального приближения к решению ![]() и соответствующие функции
и соответствующие функции ![]() ,
, ![]() ;
; ![]()
Лучшие результаты вычислительных экспериментов, выполненных при помощи алгоритма CIAC-S, представлены на рисунке 20. Ему соответствует угол ![]() , угловая скорость вала
, угловая скорость вала![]()
 и расход энергии
и расход энергии ![]() .
.
4.2. Алгоритм HCIAC-M
Максимальное число оценок целевой функции в процессе локального поиска ограничиваем величиной ![]() , число запусков алгоритма локального поиска полагаем равным
, число запусков алгоритма локального поиска полагаем равным ![]() .
.

а) ![]()
б) ![]()
в) ![]()
Рисунок 20 – Результаты решения задачи – оптимальная функция ![]() и соответствующие функции
и соответствующие функции ![]() ,
, ![]() ;
; ![]() ; алгоритм CIAC-S
; алгоритм CIAC-S
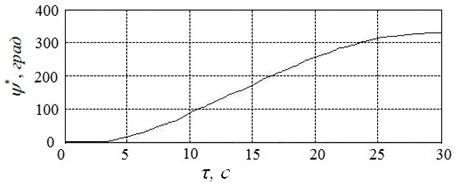
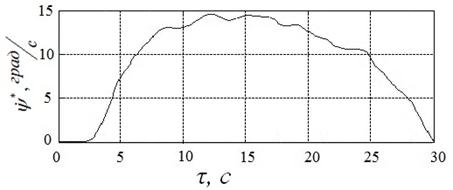
Результаты решения задачи с помощью алгоритма HCIAC-M, полученные в условиях п.4.1, иллюстрирует рисунок 21. Представленному решению соответствует угол ![]() , угловая скорость вала
, угловая скорость вала ![]()
 и расход энергии
и расход энергии ![]() .
.
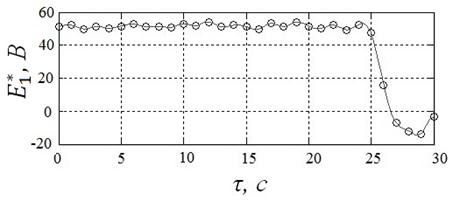
а) ![]()
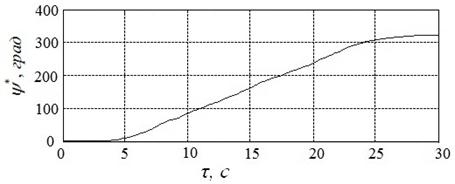
б) ![]()

в) ![]()
Рисунок 21 – Результаты решения задачи – оптимальная функция ![]() и соответствующие функции
и соответствующие функции ![]() ,
, ![]() ;
; ![]() ; алгоритм HCIAC-M
; алгоритм HCIAC-M
Из рисунков 20, 21 следует, что, как и ожидалось, алгоритм HCIAC-M обеспечивает повышение точности решения и позволяет получить более гладкий управляющий сигнал. Вследствие увеличения числа испытаний скорость поиска замедляется по сравнению с алгоритмом CIAC-Sпримерно на 30%.
Заключение
Представленные результаты исследования позволяют сделать вывод, что предложенная мультимемеевая гибридизация муравьиного алгоритма HCIACпозволяет не только увеличить вероятность локализации глобального экстремума целевой функции, но и повысить точность решения. Кроме того, за счет повышения эффективности поиска, гибридный алгоритм дает возможность уменьшить число агентов в системе и повысить тем самым его быстродействие. Мультимемеевая гибридизация приводит к алгоритму, обладающему свойствами самоадаптации, поскольку в процессе поиска мемы конкурируют между собой и победивший на данном этапе поиска мем используется на последующих этапах.
В развитие работы авторы планируют использовать расширенный набор мемов, выбирать наилучших мемов для различных подобластей пространства поиска. Планируется также параллельная реализация рассматриваемых алгоритмов.
Список литератуы
1. Карпенко А.П., Чернобривченко К.А. Эффективность оптимизации методом непрерывно взаимодействующей колонии муравьев (CIAC) // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 2. Режим доступа: http://technomag.edu.ru/doc/165551.html (дата обращения 20.10.2012).
2. Dréo J., Siarry P. Continuous interacting ant colony algorithm based on dense heterachy // Future Generation Computer Systems. 2004. Vol. 20, no. 5. P. 841–856. DOI: http://dx.doi.org/10.1016/j.future.2003.07.015
3. Dreo J., Siarry P. Hybrid Continuous Interacting Ant Colony aimed at enhanced global optimization // Algorithmic Operations Research. 2007. Vol. 2, no. 1. P. 52–64.
4. Krasnogor N. Studies on the Theory and Design Space of Memetic Algorithms : Ph.D. Thesis. Faculty of Computing, Mathematics and Engineering, University of the West of England, Bristol, U.K, 2002. 289 p.
5. Karpenko A.P., Svianadze Z.O. Meta-optimization based on self-organizing-map and genetic algorithm // Optical Memory and Neural Networks (Information Optics). 2011. Vol. 20, No. 4. P. 279-283. DOI: 10.3103/S1060992X11040059
6. Tang K., Yao X., Suganthan P.N., MacNish C., Chen Y.P., Chen C.M., Yang Z. Benchmark Functions for the CEC'2008 Special Session and Competition on Large Scale Global Optimization. Nature Inspired Computation and Applications Laboratory, USTC, China, 2007.
7. Александров А.Г. Оптимальные и адаптивные системы. М.: Высшаяшкола, 1989. 263 с.
8. Hu X.-M., Zhang J., Li Y. Orthogonal Methods Based Ant Colony Search for Solving Continuous Optimization Problems // Journal of Computer Science and Technology. 2008. Vol. 23, no. 1. P. 2-18. DOI: 10.1007/s11390-008-9111-5
9. MatLab, Optimization Toolbox Fminunc. Центркомпетенции MathWorks. Режимдоступа: http://matlab.exponenta.ru (дата обращения 20.10.20120).
10. Федоренко Р.П. Приближенное решение задач оптимального управления. М.: Наука, 1978. 488 с.
Публикации с ключевыми словами: глобальная оптимизация, муравьиный алгоритм, мем
Публикации со словами: глобальная оптимизация, муравьиный алгоритм, мем
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



