научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2012
DOI: 10.7463/1012.0469199
УДК 621.7.043
Россия, МГТУ им. Н.Э. Баумана
Введение
Высокоточные облицовки сферической формы широко применяются в современных системах вооружений, ракетно-космической технике и других областях машиностроения.
Типовая технология получения таких облицовок включает операцию калибровки внутренней поверхности данной детали, позволяет обеспечить точность формы и, в дальнейшем, при механической обработке снизить ее разностенность [1]. Наиболее распространенным способом проведения такой операции является деформирование детали за счет внешнего гидростатического давления P до полного соприкосновения ее внутренней поверхности, имеющей в начале операции радиус Rз, высоту H и толщину ![]() , с поверхностью матрицы радиусом Rм (рис. 1). При этом Rз>Rм. В качестве сред, передающих внешнее воздействие, могут выступать жидкости, резины, эластичные пластики типа полиуретанов, достоинством применения которых является равномерное распределение давления нагружения по поверхностям контакта с калибруемой деталью [2].
, с поверхностью матрицы радиусом Rм (рис. 1). При этом Rз>Rм. В качестве сред, передающих внешнее воздействие, могут выступать жидкости, резины, эластичные пластики типа полиуретанов, достоинством применения которых является равномерное распределение давления нагружения по поверхностям контакта с калибруемой деталью [2].

Рис. 1. Схема проведения калибровки
1 – калибруемая сферическая облицовка; 2 – сферическая матрица
Эффект пружинения детали, возникающий после снятия внешнего воздействия, затрудняет проектирование технологического процесса изготовления изделий и требует проведения мероприятий по его компенсации. В связи с этим, с целью минимизации затрат времени и материальных ресурсов на определение параметров и режимов проведения калибровки могут быть использованы различные методы априорных оценок величины пружинения. В большинстве из них используется математическое моделирование для определения параметров проведения процессов штамповки и калибровки. Допущения, принятые в подобных методиках, зачастую несут в себе серьезные ограничения в их применимости. Например, методики [3-5] могут быть успешно использованы только для оценки величины пружинения деталей простой формы (пластин, втулок, сферических облицовок). Более того, использование безмоментной теории оболочек не позволяет применять данные модели к деталям, толщиной которых нельзя пренебречь, таким, например, как сферическая облицовка, рассматриваемая в настоящей статье.
В работе [6] показано, что применение современных конечно-элементных систем моделирования позволяет с удовлетворительной точностью оценивать величину пружинения откалиброванных деталей сложной конфигурации и значительной толщины. Однако широкий круг охвата различных инженерных задач, универсальная направленность современных систем конечно-элементного моделирования порождают ряд существенных особенностей, связанных с их применением на практике. Данные особенности заключаются в использовании ресурсоемких алгоритмов проведения расчетов, в относительной сложности освоения конечным пользователем, а также в высокой стоимости таких систем. При проектировании технологических процессов наиболее предпочтительным является использование упрощенных инженерных подходов для определения оптимальных режимов и условий проведения составляющих эти процессы операций.
Задачами данной работы являются анализ напряженно-деформированного состояния, а также получение аналитических выражений для оценки величины пружинения толстостенных облицовок сферической формы при калибровке жидкими и эластичными средами. Поиск зависимостей осуществлялся путем обработки ряда численных расчетов процессов калибровки, выполненных с использованием метода конечных элементов, средствами множественного регрессионного анализа.
Численное моделирование калибровки облицовки сферической формы и анализ полученных результатов
При построении расчетной модели калибровки облицовок сферической формы были использованы допущения и предположения, хорошо зарекомендовавшие себя [6]:
1) для моделирования использовался метод неявного анализа (h-метод) и программная среда ANSYSAPDL [7];
2) принимая во внимание тот факт, что деталь и матрица имеют единую ось симметрии, при моделировании рассматривалась четверть этих объектов;
3) для разбиения детали использовался конечный элемент Solid 186 [7];
4) матрица моделировалась абсолютно жесткой поверхностью;
5) давление жидкости равномерно распределялось по внешней и торцевой поверхности детали (рис. 1);
6) изменение давления P происходило по закону, представленному на рис. 2;
7) трение поверхностей калибруемой детали и матрицы не учитывалось;
8) в детали отсутствовали начальные напряжения (калибровка после отжига);
9) в качестве модели материала облицовки использовалась билинейная зависимость интенсивности напряжений ![]() и деформаций
и деформаций ![]() с кинематическим упрочнением (рис. 3).
с кинематическим упрочнением (рис. 3).

Рис. 2 Характер изменения давления P в процессе моделирования калибровки

Рис. 3. Билинейная модель поведения материала
E – модуль Юнга; ![]() - предел текучести;
- предел текучести; ![]() - модуль упрочнения
- модуль упрочнения
Пружинение детали П определялось как модуль вектора перемещения точек, принадлежащей внутренней поверхности детали, после разгрузки, что соответствует максимальной деформации детали вследствие упругого пружинения (рис. 4).
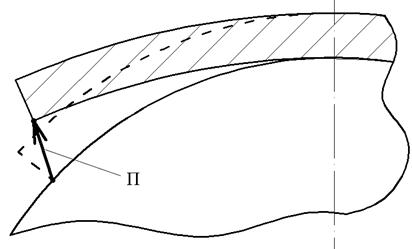
Рис. 4. Перемещение облицовки в процессе разгрузки.
П – величина пружинения
При проведении расчетов пропорции геометрических параметров облицовки были подобраны в соответствии с характеристиками типовых деталей, применяемых на практике: материал – сталь Ст3; калибровка на обжим проводилась в матрицу Rм = 52 мм; максимум давления воздействия Pк = 80 МПа; начальный радиус облицовки Rз = 57,2 мм; толщина облицовки ![]() = 2,1 мм.
= 2,1 мм.
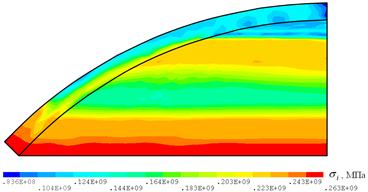
Подтверждением корректности использования симметрии задачи с целью минимизации расчетов, а также правильности выбора граничных условий служит осесимметричное распределение модуля вектора перемещения узлов детали r (рис. 5). В целом, аналогичную картину демонстрирует и распределение интенсивностей напряжений ![]() на различных стадиях калибровки (рис. 6). Необходимо отметить неравномерность напряжений в меридиональном направлении, что объясняется наличием внешнего воздействия на торцевую поверхность облицовки.
на различных стадиях калибровки (рис. 6). Необходимо отметить неравномерность напряжений в меридиональном направлении, что объясняется наличием внешнего воздействия на торцевую поверхность облицовки.
Как видно из рисунка рис. 6а, очаги пластических деформаций в соответствии с условием начала пластичности Хубера – Мизеса [8] на стадии нагружения возникают в основании детали, а также средней ее части, прилегающей к матрице. Однородность интенсивностей напряжения ![]() по толщине у основания облицовки на стадии нагружения объясняется наличием действующего на торец давления. При этом разгрузка основания происходит неравномерно по толщине – наиболее интенсивно напряжения снижаются у поверхности, к которой прикладывается внешнее воздействие (рис. 6б). Наименее всего подвергается разгрузке пограничная с матрицей область детали (внутренняя поверхность). Так, например, в средней части облицовки интенсивности остаточных напряжений
по толщине у основания облицовки на стадии нагружения объясняется наличием действующего на торец давления. При этом разгрузка основания происходит неравномерно по толщине – наиболее интенсивно напряжения снижаются у поверхности, к которой прикладывается внешнее воздействие (рис. 6б). Наименее всего подвергается разгрузке пограничная с матрицей область детали (внутренняя поверхность). Так, например, в средней части облицовки интенсивности остаточных напряжений ![]() принимают значения близкие к пределу текучести материала
принимают значения близкие к пределу текучести материала ![]() = 235 МПа. Графики (рис. 7) демонстрируют изменение интенсивности напряжений
= 235 МПа. Графики (рис. 7) демонстрируют изменение интенсивности напряжений ![]() в узлах 1, 2, 3 модели, лежащих в меридиональном сечении детали (рис. 6б), на стадиях стационарного нагружения и разгрузки.
в узлах 1, 2, 3 модели, лежащих в меридиональном сечении детали (рис. 6б), на стадиях стационарного нагружения и разгрузки.
Из графиков 7 видно, что узлы 1 и 2 деформируются упруго, однако после снятия внешнего воздействия напряжения в них не разгружаются полностью. Причиной тому является влияние пластически деформированных частей облицовки.
Высокие остаточные напряжения могут приводить к ухудшению эксплуатационных характеристик детали и изделия в целом. Для снижения остаточных напряжений после калибровки в ряде случаев целесообразно применять операцию отжига.
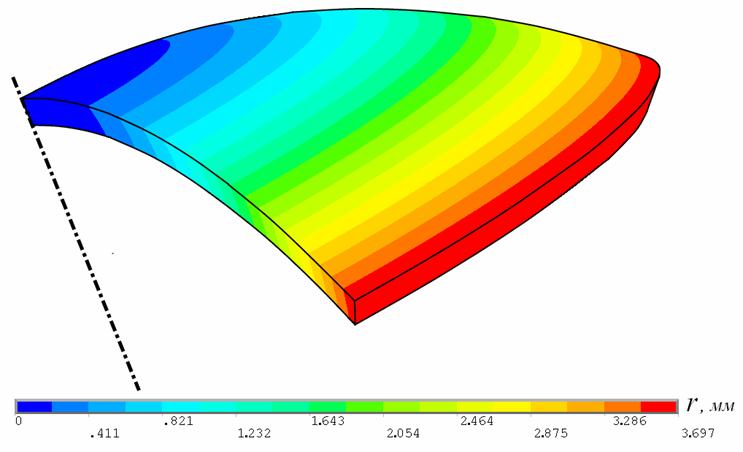
Рис. 5. Модуль вектора перемещения узлов облицовки r в конечный момент времени
|
|
а) | б) |
Рис. 6. Интенсивность напряжений
| |
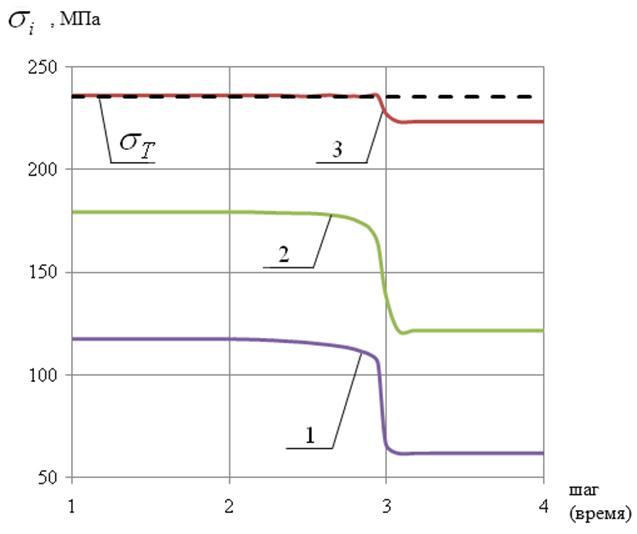
Рис. 7. Изменение интенсивности напряжений ![]() в процессе калибровки в узлах 1, 2, 3, изображенных на рис. 6б
в процессе калибровки в узлах 1, 2, 3, изображенных на рис. 6б
Построение аналитических выражений для оценки пружинения облицовок сферической формы
В качестве величин, оказывающих решающее влияние на результат калибровки, были выбраны следующие факторы (число факторов p=4): начальный радиус Rз, начальная толщина ![]() , начальная высота H облицовки, максимальное давление нагружения при калибровке Pк.
, начальная высота H облицовки, максимальное давление нагружения при калибровке Pк.
Предполагая, что зависимость между факторами и величиной пружинения является линейной, для построения искомых аналитических выражений был использован метод множественного регрессионного анализа [9]. В соответствии с планом полного факторного эксперимента каждый фактор принимал два значения. Таким образом, для построения связи проводилось ![]() численных расчетов, выполняемых с учетом вышеприведенного подхода. В рамках одного плана параметры материала детали принимались неизменными.
численных расчетов, выполняемых с учетом вышеприведенного подхода. В рамках одного плана параметры материала детали принимались неизменными.
Значения факторов, представленные ниже в безразмерном виде, выбирались в соответствии с диапазоном изменения конструктивных параметров штатных изделий: радиус  , толщина
, толщина 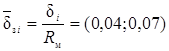 , высота
, высота 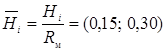 облицовки; величина максимальной внешней нагрузки
облицовки; величина максимальной внешней нагрузки 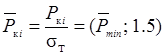 , где
, где ![]() - величина обезразмеренного минимального давления, необходимого для закрытия зазора между матрицей и облицовкой.
- величина обезразмеренного минимального давления, необходимого для закрытия зазора между матрицей и облицовкой.
Расчеты величины пружинения проводились для детали, выполненной из меди марки М1 и стали Ст3 (таблица 1).
Таблица 1
Исходные данные и результаты численных расчетов
Матрица планирования численных расчетов | Результаты расчетов | |||||||
j | 1 | 2 | 3 | 4 | Пружинение | |||
i | Радиус облицовки
| Толщина облицовки
| Высота облицовки
| Давление | Ст3 | М1 | ||
Ст3 | М1 | |||||||
1 | 1,1 | 0,04 | 0,15 | 0,34 | 0,33 | 2,75 | 2,50 | |
2 | 1,3 | 0,04 | 0,15 | 0,34 | 0,33 | 2,10 | 1,90 | |
3 | 1,1 | 0,07 | 0,15 | 0,34 | 0,33 | 2,15 | 1,94 | |
4 | 1,3 | 0,07 | 0,15 | 0,34 | 0,33 | 1,81 | 1,56 | |
5 | 1,1 | 0,04 | 0,30 | 0,34 | 0,33 | 2,75 | 2,42 | |
6 | 1,3 | 0,04 | 0,30 | 0,34 | 0,33 | 2,25 | 1,90 | |
7 | 1,1 | 0,07 | 0,30 | 0,34 | 0,33 | 2,54 | 2,33 | |
8 | 1,3 | 0,07 | 0,30 | 0,34 | 0,33 | 2,19 | 1,90 | |
9 | 1,1 | 0,04 | 0,15 | 1,50 | 1,50 | 2,79 | 2,52 | |
10 | 1,3 | 0,04 | 0,15 | 1,50 | 1,50 | 2,06 | 1,75 | |
11 | 1,1 | 0,07 | 0,15 | 1,50 | 1,50 | 2,19 | 1,92 | |
12 | 1,3 | 0,07 | 0,15 | 1,50 | 1,50 | 1,54 | 1,23 | |
13 | 1,1 | 0,04 | 0,30 | 1,50 | 1,50 | 2,79 | 2,44 | |
14 | 1,3 | 0,04 | 0,30 | 1,50 | 1,50 | 2,08 | 1,98 | |
15 | 1,1 | 0,07 | 0,30 | 1,50 | 1,50 | 2,56 | 2,29 | |
16 | 1,3 | 0,07 | 0,30 | 1,50 | 1,50 | 1,88 | 1,54 | |
На основе приведенных данных (таблица 1) установлена зависимость между начальными параметрами задач (факторами) и величинами упругого пружинения детали ![]() , используя предположение, что искомая связь описывается линейным многочленом вида
, используя предположение, что искомая связь описывается линейным многочленом вида
 , (1)
, (1)
где p - число факторов калибровки (p = 4), ![]() - безразмерная постоянная составляющая пружинения,
- безразмерная постоянная составляющая пружинения, ![]() - безразмерные коэффициенты влияния j-ого фактора на величину пружинения,
- безразмерные коэффициенты влияния j-ого фактора на величину пружинения, ![]() - безразмерное значение j-ого фактора.
- безразмерное значение j-ого фактора.
Значения коэффициентов выражения вида (1) для деталей из стали Ст3 и меди М1, найденные с использованием линейного множественного регрессионного анализа, приведены в таблице 2.
Таблица 2
Значения коэффициентов уравнения регрессии
j | Коэффициент влияния | Материал | |
Ст3 | М1 | ||
постоянная составляющая |
|
| |
1 | радиуса облицовки |
|
|
2 | толщины облицовки |
|
|
3 | высоты облицовки |
|
|
4 | максимального давления |
|
|
Теснота связи между результатами наблюдений и оценками, проведенными по полученным выражениям, была установлена путем вычисления коэффициента множественной корреляции R. Величина R для деталей, выполненных из меди марки М1, составила 0,92, для стальных облицовок – 0,93. Значимость коэффициента множественной корреляции была также оценена при помощи F-критерия Фишера для уровня значимости 0,01. Связь считают статистически значимой в том случае, если расчетное значение ![]() ,
, ![]() превышает табличное
превышает табличное ![]() [9].
[9].
Аналогично по t-критерию Стьюдента для уровня значимости 0,01: ![]() ,
, ![]() являются величинами большими значения, полученного из таблицы
являются величинами большими значения, полученного из таблицы ![]() [9].
[9].
Близкие к единице значения коэффициента множественной корреляции R, а также широкий доверительный интервал подтверждают гипотезу о линейном характере зависимости величины пружинения от выбранных факторов в заданном диапазоне их варьирования.
Полученные линейные выражения позволяют провести оценку пружинения детали типа сферическая облицовка (рис. 1), величина прикладываемого внешнего воздействия, а также размеры, которой лежат в диапазоне варьирования выбранных факторов калибровки.
Оценка пружинения с использованием выражения (1) может осуществляться для различных значений радиуса матрицы Rм, что подтверждается численными расчетами. Было выполнено моделирование процесса калибровки по варианту i=2 (таблица 1) с размерами, увеличенными в два раза (в том, числе и радиус матрицы). Давление нагружения Pк подбиралось как минимально необходимое для полного закрытия зазора между матрицей и облицовкой и составило 85 МПа. В качестве материала была использована сталь Ст3. Полученная величина пружинения 0,225 мм оказалась близка к значению 0,218 мм, оцененному по линейной зависимости (1).
Анализ полученных выражений для оценки пружинения
Характер воздействия факторов на величину пружинения определяется знаком коэффициентов влияния ![]() . Отрицательная величина коэффициентов влияния радиуса, толщины детали, а также прикладываемого давления говорит о том, что данные факторы стремятся снизить пружинение. Сходность знаков коэффициентов уравнений регрессии и значений коэффициентов геометрических факторов, полученных для облицовок, выполненных из стали Ст3 и сплава М1, подтверждает индифферентность характера их влияния к материалу образцов.
. Отрицательная величина коэффициентов влияния радиуса, толщины детали, а также прикладываемого давления говорит о том, что данные факторы стремятся снизить пружинение. Сходность знаков коэффициентов уравнений регрессии и значений коэффициентов геометрических факторов, полученных для облицовок, выполненных из стали Ст3 и сплава М1, подтверждает индифферентность характера их влияния к материалу образцов.
При помощи полученных зависимостей были установлены относительные значения вкладов, которые вносят факторы в переменную часть уравнения регрессии (рис. 8Р). Диаграмма вкладов построена для величин факторов, указанных в пункте i=13 матрицы планирования (таблица 1).
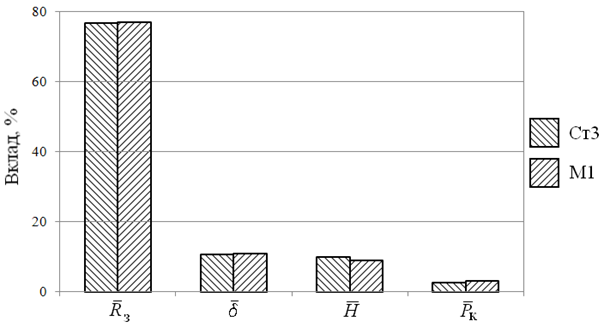
Рис. 8 Диаграмма вкладов факторов в переменную составляющую уравнения регрессии
Диаграмма демонстрирует качественное совпадение распределения вкладов факторов для медной и стальной облицовок. Наибольшее возмущение в пружинение вносит начальный радиус ![]() , далее, в порядке убывания следует толщина
, далее, в порядке убывания следует толщина ![]() и высота
и высота ![]() детали. Наименьший вклад оказывает давление нагружения
детали. Наименьший вклад оказывает давление нагружения ![]() .
.
На основе приведенной диаграммы вкладов, а также значений коэффициентов влияния, можно сделать вывод о том, что для уменьшения величины пружинения необходимо калибровать облицовки с бо́льшим припуском на механообработку (с бо́льшим радиусом сферической поверхности и толщиной). Повышение величины максимального давления калибровки приводит к незначительному уменьшению пружинения. Исходя из этого, данной параметр рекомендуется принимать минимально необходимым для полного закрытия зазора между матрицей и деталью, что согласуется с общепринятой практикой.
Анализ полученных выражений вида (1) показал, что устранение пружинения за счет выбора размеров облицовки и усилия воздействия не представляется целесообразным:
1) увеличение радиуса ![]() и толщины
и толщины ![]() детали повышает трудоемкость последующих операций механообработки, а также ведет к неэффективному использованию материала;
детали повышает трудоемкость последующих операций механообработки, а также ведет к неэффективному использованию материала;
2) увеличение давления ![]() при калибровке приводит к сравнительно небольшому изменению пружинения детали и к тому же имеет свои пределы.
при калибровке приводит к сравнительно небольшому изменению пружинения детали и к тому же имеет свои пределы.
Необходимо отметить, что в условиях реального производства пружинение является случайной величиной вследствие действия сил технологической природы, которая характеризуется полем рассеяния относительно номинальной величины. В отличие от номинального значения пружинения ![]() , являющегося функцией режимов проведения калибровки, его случайная составляющая
, являющегося функцией режимов проведения калибровки, его случайная составляющая ![]() представляет собой объективную характеристику технологического оснащения и не может быть скомпенсирована без существенного вмешательства в технологический процесс.
представляет собой объективную характеристику технологического оснащения и не может быть скомпенсирована без существенного вмешательства в технологический процесс.
Получим выражение для оценки ![]() как полный дифференциал
как полный дифференциал ![]() , считая факторы независимыми величинами, и запишем выражение в приращениях [10]
, считая факторы независимыми величинами, и запишем выражение в приращениях [10]
![]() , (2)
, (2)
где ![]() .
.
Таким образом, для оценки рассеяния величины пружинения необходимо определить диапазоны колебания факторов, которые могут быть получены по результатам измерений партии деталей перед калибровкой, а также из паспортных данных прессового оборудования. При помощи выражения (2) может быть решена и обратная задача: нахождение оптимальных значений допусков на поля рассеяния факторов по заданной величине ![]() , которая, по сути, является допуском на отклонение формы сферической поверхности облицовки.
, которая, по сути, является допуском на отклонение формы сферической поверхности облицовки.
Выводы
1) Численными расчетами нагрузки и последующей разгрузки детали типа сферическая облицовка при калибровке установлено наличие значительных остаточных напряжений в ее материале.
2) На основе численных расчетов получены уравнения линейной регрессии для оценки пружинения деталей типа сферическая облицовка, выполненных из Ст3 и М1.
3) Анализ полученных соотношений показал, что для деталей типа сферическая облицовка:
а) наибольшее влияние на величину пружинения оказывает радиус облицовки ![]() ;
;
б) добиться полного отсутствия пружинения, изменяя значения параметров деталей и величины прикладываемого давления, не удается;
в) величину внешнего воздействия при калибровке на обжим рационально принимать минимально необходимой для полного закрытия начального зазора между облицовкой и матрицей.
Список литературы
1. Тарасов В.А., Баскаков В.Д., Круглов П.В. Методика проектирования технологии изготовления высокоточных деталей боеприпасов // Оборонная техника. - 2000. - № 1-2. - С. 89-92.
2. Исаченков Е.И. Штамповка резиной и жидкостью. – М.: Машиностроение, 1967. – 367 с.
3. Тарасов В.А., Боярская Р.В., Филимонов А.С. Взрывная калибровка сложнопрофильных тонкостенных оболочек // Вещества, материалы и конструкции при интенсивных динамических воздействиях. Труды международной конференции V Харитоновские тематические научные чтения. – 2003. – С. 510-514.
4. Чумадин А.С. Решение пластических и упругих задач листовой штамповки // Кузнечно-штамповочное производство. Обработка материалов давлением. Специальный выпуск. – 2010. – С. 11-15.
5. Анучин М.А., Полушин А.Г. Остаточные напряжения после сжатия предварительно напряженной пластины // Известия высших учебных заведений. Машиностроение.- 1978.- № 1.- С. 122-127.
6. Софьин А.С., Стрижков А.В., Ульвис Н.В., Зарубина О. В., Боярская Р. В. Численное моделирование процесса калибровки осесимметричных деталей жидкой технологической средой // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн.– 2012. – № 4. – Режим доступа: http://technomag.edu.ru/doc/361706.html (дата обращения 06.10.2012).
7. Mechanical APDL. ANSYS 13 Help system. [Electronic data and program] / ANSYS, Inc. —Canonsburg (PA), 2010.
8. Малинин Н.Н. Прикладная теория пластичности и ползучести: учебник для студентов вузов.- 2-е изд., перераб. и доп.- М.: Машиностроение, 1975. – 400 с.
9. Львовский Е.Н. Статистические методы построения эмпирических формул: учеб. пособие для втузов. – 2-е изд., перераб. и доп. – М.: Высшая школа, 1988. – 239 с.
10. Тарасов В.А., Кашуба Л.А. Теоретические основы технологии ракетостроения.– М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 352 с.
8. Малинин Н.Н. Прикладная теория пластичности и ползучести. Учебник для студентов вузов. Изд. 2-е перераб. и доп. М., Машиностроение. – 1975. – 400 с.
9. Львовский Е.Н. Статистические методы построения эмпирических формул: Учеб. пособие для втузов. – 2-е изд., перераб. и доп. – М.: Высш.шк., 1988. – 239 с.: ил.
10. Теоретические основы технологии ракетостроения / В.А. Тарасов, Л.А. Кашуба.– М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 352 с.
Публикации с ключевыми словами: метод конечных элементов, пружинение, калибровка жидкими и эластичными средами, сферическая облицовка
Публикации со словами: метод конечных элементов, пружинение, калибровка жидкими и эластичными средами, сферическая облицовка
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||