научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2012
DOI: 10.7463/0612.0423283
УДК 519.6
Россия, МГТУ им. Н.Э. Баумана
Введение
Постановка задачи многокритериальной оптимизации (МКО-задачи) фиксирует множество допустимых значений вектора варьируемых параметров задачи и вектор критериальных функций. Данная информация позволяет обычно выделить не одно решение задачи, а лишь ее множество Парето. Поэтому часто говорят, что решением МКО-задачи является множество Парето этой задачи. Множество Парето и фронт Парето занимают в теории многокритериальной оптимизации исключительное место еще и потому, что согласно известному принципу Эджворта-Парето, при «разумном» поведении лица, принимающего решения (ЛПР), выбор решения следует производить на множестве Парето [1].
Классические методы решения МКО-задачи основаны на использовании, помимо указанной информации о задаче, еще тем или иным образом формализованной информации о предпочтениях ЛПР. В результате задачу удается свести к совокупности задач глобальной однокритериальной оптимизации. Относительно новый и быстро развивающийся класс методов решения МКО-задачи образуют методы Парето-аппроксимации, предполагающие предварительное построение некоторой конечномерной аппроксимации множества, а тем самым, и фронта Парето.
Известно большое число популяционных и непопуляционных методов построения Парето-аппроксимации (см., например, обзор [2]). Работа посвящена исследованию эффективности, так называемого, метода адаптивных взвешенных сумм (AdaptiveWeightedSummethod, AWS-method), который предложили и разработали Рю, Ким и Ван (J-H. Ryu, S. Kim, H. Wan) [3]. Для решения задачи Парето-аппроксимации метод AWS использует аддитивную свертку частных критериев оптимальности. Однако в отличие от классического метода суммы взвешенных критериев (WeightedSummethod, WS-method) [1], также использующего такую свертку, метод AWSпредполагает адаптацию весовых коэффициентов в процессе итераций на основе информации о текущем положении подобласти поиска. Целью разработки метода AWSбыло преодоление известного недостатка метода WS, заключающегося в невозможности локализации точек множества Парето, которые соответствуют вогнутым фрагментам фронта Парето.
Для сокращения затрат на вычисление значений критериальных функций метод AWSиспользует метамодели этих функций. Поскольку в практически значимых задачах вычислительная сложность критериальных функций обычно является высокой, это обстоятельство позволяет сократить вычислительные затраты и делает метод, на наш взгляд, весьма перспективным. Недостатком метода AWSв существующем виде является его ориентация на решение только двухкритериальных задач Парето-аппроксимации.
Выполненное авторами метода AWSисследование показало его высокую эффективность. Однако исследование было выполнено всего для двух относительно простых тестовых задач многокритериальной оптимизации [3]. В данной работе мы повторяем исследование для указанных тестовых задач, а также дополнительно проводим исследование для трех других сложных тестовых задач.
В содержательных терминах качество Парето-аппроксимации может быть оценено с помощью следующих характеристик:
‑ близость найденных решений к точному множеству Парето рассматриваемой МКО-задачи;
‑ равномерность распределения решений в полученной Парето-аппроксимации;
‑ мощность найденного множества решений.
Известно большое число индикаторов качества, формализующих указанные характеристики [4, 5]. В данной работе в качестве индикатора качества Парето-аппроксимации используем мощность найденной аппроксимации.
В первом разделе даем постановку МКО-задачи и схему метода AWS. Во втором разделе рассматриваем программную реализацию метода и организация экспериментов. В третьем разделе представлены результаты экспериментов и их обсуждение. В заключении сформулированы основные выводы и перспективы развития работы.
Научная новизна работы заключается в исследовании эффективности Парето-аппроксимации методом AWS на тестовых задачах, на которых ранее его эффективность не исследовалась. Результаты исследования выявили ряд ограничений метода и сложностей его использования. Это позволило наметить пути модификации метода, направленные на преодоление этих ограничений и сложностей.
1. Постановка задачи и схема метода
Пусть множеством допустимых значений вектора варьируемых параметров Xявляется ограниченное и замкнутое множество ![]() . Положим, что критериальная вектор-функция
. Положим, что критериальная вектор-функция ![]() со значениями в критериальном пространстве
со значениями в критериальном пространстве ![]() определена в области
определена в области ![]() . ЛПР стремится минимизировать в этой области каждый из частных критериев оптимальности
. ЛПР стремится минимизировать в этой области каждый из частных критериев оптимальности ![]() , что условно записываем в виде
, что условно записываем в виде
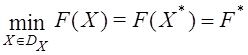 , (1)
, (1)
где векторы ![]() ‑искомое решение задачи многокритериальной оптимизации.
‑искомое решение задачи многокритериальной оптимизации.
Здесь и далее запись вида ![]() , где
, где ![]() - вектор или некоторое счетное множество, означает размерность этого вектора или мощность множества соответственно. Полагаем, что частные критерии оптимальности тем или иным образом нормализованы, так что
- вектор или некоторое счетное множество, означает размерность этого вектора или мощность множества соответственно. Полагаем, что частные критерии оптимальности тем или иным образом нормализованы, так что ![]() для любого
для любого ![]() ;
; ![]() .
.
Вектор-функция ![]() выполняет отображение множества
выполняет отображение множества ![]() во множество
во множество ![]() , которое называется множеством достижимости. Множество и фронт Парето обозначаем
, которое называется множеством достижимости. Множество и фронт Парето обозначаем ![]() ,
, ![]() , а их конечномерные аппроксимации
, а их конечномерные аппроксимации ![]() ,
, ![]() соответственно. Последние множества называем архивными.
соответственно. Последние множества называем архивными.
Метод AWS включает в себя три следующие основные процедуры:
‑ определение центральной точки;
‑ формирование метамоделей частных критериев оптимальности;
‑ решение полученных оптимизационных задач.
Рассмотрим суть указанных процедур.
Определение центральной точки. На этапе инициализации центральную точку ![]() выбираем случайным образом в области
выбираем случайным образом в области ![]() . На этом же этапе должны быть определены следующие свободные параметры алгоритма:
. На этом же этапе должны быть определены следующие свободные параметры алгоритма: ![]() ‑ начальный радиус области доверия (trustregionradius);
‑ начальный радиус области доверия (trustregionradius); ![]() ‑ коэффициент сужения этой области;
‑ коэффициент сужения этой области; ![]() ‑ минимальная величина радиуса области.
‑ минимальная величина радиуса области.
На итерации ![]() центральную точку
центральную точку ![]() отыскиваем среди точек текущей Парето-аппроксимации
отыскиваем среди точек текущей Парето-аппроксимации ![]() , построенной на предыдущей итерации
, построенной на предыдущей итерации ![]() .
.
Отсортируем элементы архивных множеств ![]() по возрастанию первого частного критерия
по возрастанию первого частного критерия ![]() и представим в виде линейных списков с прежними наименованиями. Определим расстояние
и представим в виде линейных списков с прежними наименованиями. Определим расстояние ![]() архивной точки
архивной точки ![]() до ближайших к ней в списке
до ближайших к ней в списке ![]() точек формулой
точек формулой
где ![]() - евклидова норма.
- евклидова норма.
Алгоритм использует следующее правило определения центральной точки ![]() .
.
1) Если ![]() , то полагаем
, то полагаем ![]() , где
, где
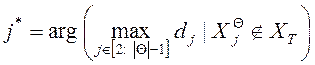 .
.
Здесь ![]()
![]() - множество точек, использованных в качестве центральных на всех предыдущих итерациях
- множество точек, использованных в качестве центральных на всех предыдущих итерациях ![]() . Иными словами, за центральную точку принимаем точку, во-первых, наиболее удаленную от других точек множества
. Иными словами, за центральную точку принимаем точку, во-первых, наиболее удаленную от других точек множества ![]() в смысле расстояния (3), и, во-вторых, не использованную на предшествующих итерациях.
в смысле расстояния (3), и, во-вторых, не использованную на предшествующих итерациях.
2) Если ![]() , то с равной вероятностью полагаем
, то с равной вероятностью полагаем ![]() или
или ![]() .
.
3) Если ![]() , то принимаем
, то принимаем ![]() .
.
Формирование метамоделей. Метамодели представляют собой квадратичные аппроксимации ![]() ,
, ![]() функций
функций ![]() ,
, ![]() в окрестности точки
в окрестности точки ![]() :
:
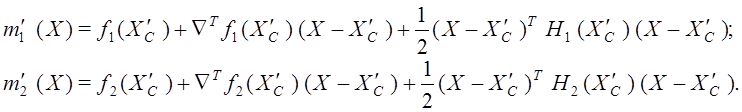
Здесь ![]() ‑ матрицы Гессе функций
‑ матрицы Гессе функций ![]() ,
, ![]() в точке
в точке ![]() .
.
Если ![]() , то дополнительно строим метамодели
, то дополнительно строим метамодели
![]() ,
,
![]() ,
,
а если ![]() или
или ![]() ‑ метамодель
‑ метамодель
![]() .
.
В первом случае (![]() ) весовые множители
) весовые множители ![]() ,
, ![]() определяем по правилу
определяем по правилу
![]() ,
,
![]() ;
;
во втором случае (![]() ) – по правилу
) – по правилу
![]() ;
;
в третьем случае (когда ![]() ) – по правилу
) – по правилу ![]() . Константы
. Константы ![]() ,
, ![]() выбираем таким образом, чтобы обеспечить выполнение условий нормировки
выбираем таким образом, чтобы обеспечить выполнение условий нормировки ![]() .
.
Отметим, что при построении метамоделей ![]() ,
, ![]() речь может идти не о градиентах и матрице Гессе функций
речь может идти не о градиентах и матрице Гессе функций ![]() ,
, ![]() , а об их оценках, полученных, например, численными методами (путем соответствующих конечно-разностных аппроксимаций указанных функций).
, а об их оценках, полученных, например, численными методами (путем соответствующих конечно-разностных аппроксимаций указанных функций).
Решение оптимизационных задач. Данная процедура предполагает решение задач оптимизации
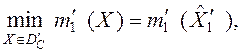
 (4)
(4)
где текущую область доверия (trustregion) ![]() определяет формула
определяет формула
![]() .
.
Если ![]() , то решения
, то решения ![]() задач (4) позволяют отыскать приближенно оптимальные по Парето точки
задач (4) позволяют отыскать приближенно оптимальные по Парето точки ![]() , принадлежащие области доверия
, принадлежащие области доверия ![]() , путем решения оптимизационных задач
, путем решения оптимизационных задач

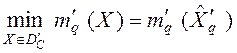 . (5)
. (5)
Данный этап алгоритмаиллюстрирует рисунок 1, на котором принято что ![]() ,
, ![]() ,
, ![]() .
.
Отметим, что задачи (4), (5) представляют собой задачи оптимизации квадратичных функций, для решения которых известны высокоэффективные методы, алгоритмы и соответствующее программное обеспечение.

Рисунок 1 – К схеме метода AWS: результаты решения задач (5)
В процессе итераций текущий радиус области доверия уменьшают по правилу ![]() до достижения минимально допустимой его величины
до достижения минимально допустимой его величины ![]() . Новое состояние архивного множества
. Новое состояние архивного множества ![]() получаем путем добавления в него точек
получаем путем добавления в него точек ![]() ,
, ![]() ,
, ![]() ,
, ![]() и исключения из полученного набора доминируемых решений. Аналогично, множество
и исключения из полученного набора доминируемых решений. Аналогично, множество ![]() образуем путем добавления в него точек
образуем путем добавления в него точек ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2. Программная реализация метода и организация экспериментов
Для решения однокритериальных задач условной оптимизации (4), (5) в программной реализации использован метод штрафных функций в совокупности с известным методом Нелдера-Мида локальной безусловной оптимизации. Вместо метамоделей критериальных функций ![]() ,
, ![]() использованы сами эти функции. Данное ограничение не является критичным, поскольку влияет на время вычислений, но не на качество Парето-аппроксимации.
использованы сами эти функции. Данное ограничение не является критичным, поскольку влияет на время вычислений, но не на качество Парето-аппроксимации.
Программа написана на языке программирования C++. Ниже представлены основные классы программной модели:
― AWSAlgorithm – класс, реализующий алгоритм AWS;
― PenaltyAlgorithm – класс, реализующий метод штрафных функций;
― NelderMidAlgorithm – класс, реализующий алгоритм Нелдера‑Мида;
― Polyhedron – вспомогательный класс, реализующий основные операции над многогранниками;
― QuickSort – класс, реализующий алгоритм «быстрой сортировки».
― Function – абстрактный класс, реализующий общий интерфейс для реализаций критериальных функций и ограничений;
― ZDT3,CompositeFunction – конкретные реализации критериальных функций;
― HyperSphereConstrain- конкретная реализация ограничений.
Эксперименты выполнены на персональном компьютере, основные параметры которого представлены ниже:
― процессор Intel Pentium Dual-Core T4500, 2,3 ГГц;
― оперативная память DDR-3, 3 Гб.
Изучалось влияние на эффективность методаследующих его свободных параметров:
‑ начальный радиус области доверия ![]() ;
;
‑ кэффициент сужения области доверия ρ;
‑ минимальная величина радиуса области доверия ![]() .
.
В качестве меры эффективности метода использована мощность множества решений (overallnon-dominatedvectorgeneration)
![]() ,
,
то есть число элементов множества ![]() [5].
[5].
Исследование выполнено на пяти следующих известных двухкритериальных тестовых задачах многокритериальной оптимизации.
Задача «о двух параболоидах» (двумерная, двухкритериальная):
![]() ;
;
![]() ,
,
![]() .
.
Задача имеет непрерывный выпуклый фронт Парето.
Задача Аудета (С. Audet):
![]() ;
;
![]() ,
,
![]() ,
,
где


Задача является двумерной, двухкритериальной, фронт Парето ‑ непрерывный, значению ![]() соответствует выпуклое множество Парето, а
соответствует выпуклое множество Парето, а ![]() ‑ невыпуклое[6].
‑ невыпуклое[6].
Задача ZDT3 (30-мерная, двухкритериальная):
![]() ;
;
![]()

где
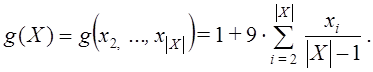
Сложность задачи обусловлена высокой размерностью, а также несвязным, хотя и выпуклым, фронтом Парето [4].
Задача ZDT6 (10-мерная, двухкритериальная):
![]() ;
;
![]() ,
,
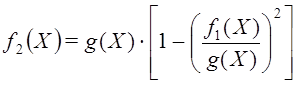 ,
,
где
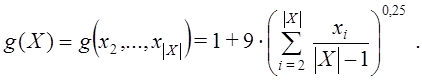
Задача имеет слабо невыпуклый фронт Парето[4]. Сложность задачи ZDT6 заключается в невыпуклости фронта и многомерности задачи.
Задача ZDT7: (30-мерная, двухкритериальная):
![]() ;
;
![]() ,
,
![]() ,
,
где


Задача имеет непрерывный выпуклый фронт Парето [4].
3. Результаты экспериментов
Задача «о двух параболоидах» (рисунок 2). Результаты решения данной задачи, в силу ее простоты, показывают, по сути, только работоспособность алгоритма и программы AWSM, реализующей этот алгоритм. Из рисунка 2 следует, что за небольшое число итераций ![]() построено множество
построено множество ![]() , состоящее из
, состоящее из ![]() недоминируемых решений. Обеспечены приемлемая плотность и равномерностью покрытия фронта Парето. Результаты исследования показывают, что варьирование значений свободных параметров метода в широком диапазоне оказывает в данном случае слабое влияние на качество Парето-аппроксимации.
недоминируемых решений. Обеспечены приемлемая плотность и равномерностью покрытия фронта Парето. Результаты исследования показывают, что варьирование значений свободных параметров метода в широком диапазоне оказывает в данном случае слабое влияние на качество Парето-аппроксимации.

Рисунок 2 - Задача «о двух парабалоидах»: ![]() ;
;![]() ;
;![]() ;
; ![]()
Задача Аудета. (рисунки 3 ‑ 6). Результаты решения задачи для случая ![]() , когда фронт Парето является выпуклым, иллюстрируют рисунки 3, 4. Рисунок 3 показывает, что за
, когда фронт Парето является выпуклым, иллюстрируют рисунки 3, 4. Рисунок 3 показывает, что за ![]() итераций удалось получить только
итераций удалось получить только ![]() недоминируемых решений(против
недоминируемых решений(против ![]() решений, заявленных в исходной работе [3]). Метод не обеспечил равномерность покрытия фронта Парето. Заявленное число точек и приемлемую равномерность покрытия удалось достичь только при удвоенном числе итераций
решений, заявленных в исходной работе [3]). Метод не обеспечил равномерность покрытия фронта Парето. Заявленное число точек и приемлемую равномерность покрытия удалось достичь только при удвоенном числе итераций ![]() (рисунок 4).
(рисунок 4).
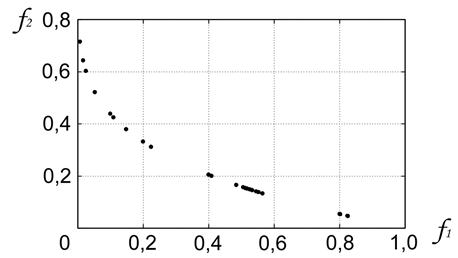
Рисунок 3 - Задача Аудета: ![]() ;
; ![]() ;
;![]() ,
, ![]() ;
; ![]()
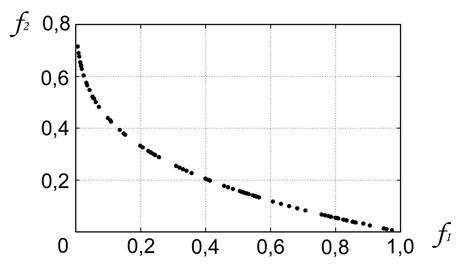
Рисунок 4 - Задача Аудета: ![]() ;
; ![]() ;
;![]() ,
, ![]() ;
; ![]()
Возможная причина указанных недостатков метода заключается в использованной в программе AWSMмодели планирования эксперимента, которая предполагает испытания только в осевых точках.
Результаты решения задачи Аудета для случая ![]() , когда фронт Парето не является выпуклым, иллюстрируют рисунки 5, 6. За
, когда фронт Парето не является выпуклым, иллюстрируют рисунки 5, 6. За ![]() итераций удалось получить только
итераций удалось получить только ![]() решений (в работе [3]для этого случая заявлено
решений (в работе [3]для этого случая заявлено![]() решений). Заявленное число точек и приемлемую равномерность покрытия фронта Парето удалось достичь только при
решений). Заявленное число точек и приемлемую равномерность покрытия фронта Парето удалось достичь только при ![]() итераций. Возможные причины отмеченных недостатков указаны выше.
итераций. Возможные причины отмеченных недостатков указаны выше.
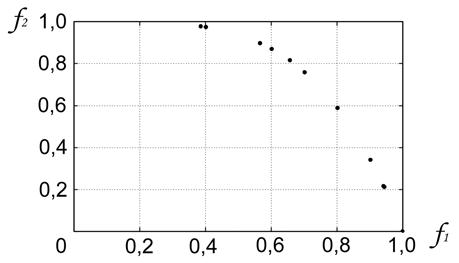
Рисунок 5 - Задача Аудета: ![]() ;
; ![]() ;
;![]() ,
, ![]() ;
; ![]()
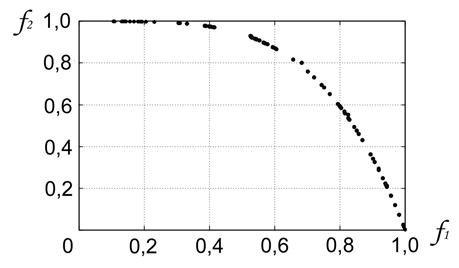
Рисунок 6 - Задача Аудета: ![]() ;
; ![]() ;
;![]() ,
, ![]() ;
; ![]()
Тщательный анализ результатов, представленных на рисунке 6, показывает, что некоторое число полученных решений не удовлетворяет ограничениям задачи. Причина появления этих решений заключается в том, что задачи глобальной условной оптимизации (4), (5) решаются в программе AWSM, как мы указывали выше, методом штрафных функций. Априорное назначение требуемой точности удовлетворения ограничений затруднительно. В то же время, как мы видим, даже кажущаяся вполне удовлетворительной точность 0,001 приводит к появлению в архиве ![]() непаретовских решений.
непаретовских решений.
Задача ZDT3 (рисунки 7, 8). Исследование показало, что качество полученной Парето-аппроксимации в данном случае сильно зависит от значений свободных параметров метода.
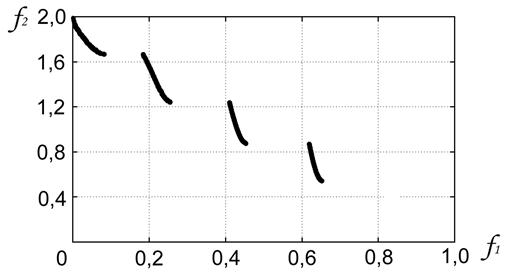
Рисунок 7 - Задача ZDT3: исходный метод; ![]() ;
;![]() ,
, ![]() ;
; ![]()
Лучший результат и соответствующие значения этих параметров иллюстрирует рисунок 8. Рисунок показывает, что метод даже для такой сложной задачи позволяет получить достаточно мощное (![]() ), плотное и равномерное покрытие фронта Парето. Для обеспечения столь высокого качества Парето-аппроксимации, потребовалось модификация исходной схемы метода, заключающаяся в разрешении использования крайних точек текущей аппроксимации
), плотное и равномерное покрытие фронта Парето. Для обеспечения столь высокого качества Парето-аппроксимации, потребовалось модификация исходной схемы метода, заключающаяся в разрешении использования крайних точек текущей аппроксимации ![]() в качестве центральных. Рисунок 7 иллюстрирует решение задачи без такой модификации.
в качестве центральных. Рисунок 7 иллюстрирует решение задачи без такой модификации.

Рисунок 8 - Задача ZDT3: модифицированный метод; ![]() ;
;![]() ,
, ![]() ;
; ![]()
Задача ZDT6 (рисунки 9, 10)оказалась наиболее сложной для данного метода. Исследование выявило, что качество полученной Парето-аппроксимации в данном случае очень сильно зависит от значений свободных параметров метода, а также от начального приближения.Так при изменении коэффициента ![]() с 1,5 до 1,6 (всего на 0,1!), метод порождает всего два решения (
с 1,5 до 1,6 (всего на 0,1!), метод порождает всего два решения (![]() ). Лучший результат, достигнутый методом, иллюстрирует рисунок 9 (
). Лучший результат, достигнутый методом, иллюстрирует рисунок 9 (![]() ). Ни равномерность, ни плотность полученной аппроксимации фронта Парето не являются приемлемыми.
). Ни равномерность, ни плотность полученной аппроксимации фронта Парето не являются приемлемыми.
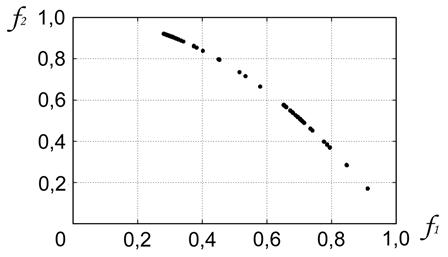
Рисунок 9 - Задача ZDT6: ![]() ;
;![]() ,
, ![]() ;
; ![]()
На рисунке 10 представлены результаты решения той же задачи с помощью генетического алгоритма. Рисунок показывает, что генетический алгоритм, в отличие от исследуемого метода AWS, не нашел ни одного решения, соответствующего условию ![]() .
.

Рисунок 10 - Задача ZDT6: генетический алгоритм
Задача ZDT7 (рисунок 11). Метод в этом случае обеспечил высокое качество Парето-аппроксимации по критериям плотности и равномерности покрытия фронта Парето при достаточно мощном архивном множестве (![]() )Исследование показало слабую зависимость качества аппроксимации от значений свободных параметров метода. Оказалось, что как и в задаче Аудета и по тем же причинам, некоторое число полученных решений не удовлетворяет ограничениям задачи.
)Исследование показало слабую зависимость качества аппроксимации от значений свободных параметров метода. Оказалось, что как и в задаче Аудета и по тем же причинам, некоторое число полученных решений не удовлетворяет ограничениям задачи.

Рисунок 11 - Задача ZDT7: ![]() ;
;![]() ,
, ![]() ;
; ![]()
Заключение
Результаты исследования показывают, что метод AWSобеспечивает высокое качество Парето-аппроксимации в случае выпуклого, хотя, быть может, и несвязного фронта Парето. Для задач, имеющих вогнутый фронт Парето, метод не всегда обеспечивает удовлетворительное качество решения или обеспечивает его, но при значительном числе итераций. В некоторых случаях метод дает недопустимые решения, обусловленные используемым способом учета ограничений на область доверия. В целом, результаты исследования показывают высокий потенциал развития метода.
В продолжение работы авторы планируют исследовать альтернативные способы учета ограничений на область доверия, различные, в том числе нейросетевые, методы построения локальных метамоделей критериальных функций. Главной задачей является распространение метода на МКО-задачи с более, чем двумя критериями оптимальности.
Работа поддержана грантом РФФИ 12-07-00324-а.
Литература
1. Ларичев О.И. Теория и методы принятия решений: Учебник для ВУЗов.- М.: Университетская книга, Логос, 2006.- 392 с.
2. Карпенко А.П., Митина Е.В., Семенихин А.С. Популяционные методы аппроксимации множества Парето в задаче многокритериальной оптимизации. Обзор // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 4. Режим доступа: http://www.technomag.edu.ru/doc/363023.html (дата обращения 08.07.2012).
3. Ryu J.-H., Kim S., Wan H. Pareto front approximation with adaptive sum method in multiobjective simulation optimization // Proceedings of the 2009 Winter Simulation Conference (WSC), 2009, Austin, pp. 623-633. Available at: http://www.informs-sim.org/wsc09papers/060.pdf , accessed 08.07.2012.
4. Zitzler E., Deb K., Thiele L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results // Evolutionary Computation, 2000, Vol. 8(2), pp. 173-195.
5. Zitzler E., Thiele L., Marco Laumanns M., Fonseca C. M., da Fonseca V. G. Performance Assessment of Multiobjective Optimizers: An Analysis and Review // IEEE Transactions of Evolutionary Computation, 2003, Vol. 7(2), pp. 117-132.
6. Audet C., Savard G., Zghal W. Multiobjective optimization through a series of single-objective formulations // SIAM Journal on Optimization, 2008, vol. 19, no. 1, pp. 188–210.
Публикации с ключевыми словами: задача многокритериальной оптимизации, аппроксимация множества Парето, метод адаптивных взвешенных сумм
Публикации со словами: задача многокритериальной оптимизации, аппроксимация множества Парето, метод адаптивных взвешенных сумм
Смотри также:
- Гибридизация методов зондирования области поиска и адаптивных взвешенных сумм в задаче Парето-аппроксимации
- Двухкритериальная идентификация кинетических параметров реакции гидроалюминирования олефинов алкилаланами
- Модифицированный метод адаптивных взвешенных сумм в задаче многокритериальной оптимизации
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



