научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 07, июль 2012
DOI: 10.7463/0712.0423252
УДК 519.6
Россия, МГТУ им. Н.Э. Баумана
Введение
Ментально-структурированный подход к обучению [1] порождает значительное число задач многокритериального принятия решений. Приведем два примера.
1) Оценка «мыслительной грамотности» учащегося требует оценки пяти следующих составляющих этой грамотности (ключевых компетенций):
- знаниевая грамотность (способность воспринимать, понимать и самостоятельно приобретать знания),
- функциональная грамотность (способность «грамотно» применять знания),
- креативная грамотность (технологические навыки порождения нового, способность к продуктивному мышлению и инновационной деятельности),
- корпоративная грамотность (способность к саморазвитию, неконфликтности групповых коммуникаций, умение принимать организационные и управленческие решения, способность доводить общее дело до конца),
- социальная грамотность (навыки духовно-нравственного межличностного общения, способность принимать социально, экономически и экологически оправданные решения).
2) Качество изложения предмета изучения определяют следующие критерии:
- антропоцентричность (опора на личностно ориентированный подход «от человека к изучаемой проблеме»),
- ментальность (изложение учебных материалов в соответствие с содержательной структурой и особенностями функционирования мозговых механизмов, в частности, в виде когнитивных карт в едином пентадно структурированном формате),
- визуализированность (оптимальное сочетание вербальной 75 % и визуальной 25 % информации),
- технологичность (использование элементов обучающих технологий, опирающихся как на функциональную асимметрию полушарий головного мозга, так и на особенности содержательного взаимодействия сознания и подсознания),
- управляемость (корректировка структурного содержания учебного процесса с позиций генетической пентадности, использование в учебных процедурах функциональных тренингов и органайзера мыслительной деятельности).
В соответствии с терминологией, принятой в теории многокритериального принятия решений [2], называем рассмотренные и иные показатели качества частными критериями оптимальности, а их совокупность – векторным критерием оптимальности.
Наряду со значениями частных критериев, определяющих грамотность учащегося, его профессионально значимые личностные качества, стиль изложения предмета изучения и так далее, в учебном процессе необходимы интегральные характеристики учащихся, преподавателей, качества учебного материала и т.д. Мы полагаем, что рассматриваемые частные и интегральные критерии оптимальности являются числовыми. Если исходные значения этих критериев представляют собой значения лингвистических переменных, то они должны быть по известным правилам преобразованы в числовые.
Переход от частных критериев оптимальности к одному числовому интегральному критерию широко используют при решении задач многокритериальной оптимизации, где этот переход реализуют с помощью различного рода скалярных сверток. Например, часто используется аддитивная свертка, представляющую собой взвешенную сумму частных критериев оптимальности [2].
Оценку значений различных частных критериев оптимальности производят, вообще говоря, разные лица, принимающие решения (ЛПР). Полагаем, что интегральную оценку на основе этих значений формирует главное лицо, принимающее решения (ГЛПР). Если способ свертки частных критериев фиксирован, то задача формирования этой оценки сводится к определению весов частных критериев оптимальности. Можно сказать, что значения этих весов формализуют функцию предпочтений ГЛПР [3].
Задачу определения весовых коэффициентов частных критериев можно рассматривать в двух постановках – априорной и апостериорной. В первом случае ГЛПР назначает веса заранее, до формирования интегральных оценок. Рассматриваем второй случай, когда ГЛПР на основе представленных ему частных оценок выставляет интегральные оценки некоторой обучающей выборке субъектов или объектов. На этой основе определяем веса частных критериев таким образом, чтобы минимизировать некоторую норму погрешности соответствующей теоретической оценки.
В конечном счете, апостериорный метод формирования значений весовых коэффициентов приводит к задаче глобальной условной многомерной оптимизации. Для решения этой задачи может быть использовано большое число детерминированных и стохастических алгоритмов [4]. Хорошо известно, что в случае отсутствия априорной информации о ландшафте целевой функции, наиболее эффективны стохастические алгоритмы глобальной оптимизации. Из числа этих алгоритмов наибольшую известность получили популяционные (метаэвристические) алгоритмы такие, как генетический алгоритм, алгоритм роя частиц, алгоритм колонии муравьев и т.д. [5]. Новизна данной работы заключается, в частности, в использовании для решения указанной задачи глобальной оптимизации перспективного алгоритма эволюции разума (Mind Evolutionary Computation, MEC) [6].
Алгоритм MEC моделирует скорее некоторые аспекты поведения человека в обществе, чем, как можно было бы предположить, работу человеческого мозга. В алгоритме MEC каждый индивид рассматривается как разумный агент, функционирующий в некоторой группе людей. При принятии решений он ощущает влияние, как со стороны членов своей группы, так и со стороны членов других групп. Точнее говоря, чтобы достичь высокого положения в обществе, индивиду приходится учиться у наиболее успешных индивидов в своей группе. В то же время, для того чтобы группа, которой принадлежит данный индивид, становилась более успешной по сравнению с другими группам, этот индивид, как и все индивиды его группы, должны руководствоваться тем же самым принципом в межгрупповой конкуренции.
Известен, так называемый, простой алгоритм MEC и несколько его модификаций – расширенный MEC [7], улучшенный MEC [6] и хаотичный MEC [8]. Мы предполагаем широкое исследование всех указанных и иных модификаций алгоритма MEC. В данной работе используем первый из указанных алгоритмов ‑ простой алгоритм эволюции разума (Simple MEC, SMEC).
Первый раздел работы содержит постановку задачи. Во втором разделе представлен используемый метод решения задачи. Третий раздел посвящен программной реализации метода. В четвертом разделе приведены результаты исследования эффективности алгоритма MEC. В пятом разделе представлены результаты численных экспериментов и их обсуждение. В заключении сформулированы основные результаты работы и перспективы ее развития.
1. Постановка задачи.
Пусть ![]() ‑ вектор рассматриваемых частных критериев оптимальности, а
‑ вектор рассматриваемых частных критериев оптимальности, а ![]() - некоторая скалярная свертка этих критериев, где
- некоторая скалярная свертка этих критериев, где ![]() - вектор весовых вещественных коэффициентов.
- вектор весовых вещественных коэффициентов.
Совокупность рассматриваемых субъектов или объектов обозначаем ![]() , а их число ‑
, а их число ‑ ![]() . Из множества
. Из множества ![]() по некоторому правилу выделяем обучающую и тестовую выборки
по некоторому правилу выделяем обучающую и тестовую выборки ![]() , числа элементов в которых равны
, числа элементов в которых равны ![]() соответственно;
соответственно; ![]() .
.
Полагаем, что оценка значений критерия ![]() произведена ЛПР с помощью числовой шкалы
произведена ЛПР с помощью числовой шкалы ![]() , где
, где ![]() ‑ нижняя и верхняя оценки соответственно. Нормализованную (см. ниже) оценку элемента
‑ нижняя и верхняя оценки соответственно. Нормализованную (см. ниже) оценку элемента ![]() по шкале
по шкале ![]() обозначаем
обозначаем ![]() , так что вектор
, так что вектор ![]() представляет собой вектор всех нормированных оценок этого элемента;
представляет собой вектор всех нормированных оценок этого элемента; ![]() .
.
Формальной оценкой элемента ![]() называем величину
называем величину ![]() ,
, ![]() . Набор формальных оценок всех элементов множества
. Набор формальных оценок всех элементов множества ![]() обозначаем
обозначаем ![]() .
.
Полагаем, что для каждого из элементов ![]() ,
, ![]() известна также назначенная ГЛПР интегральная экспертная оценка
известна также назначенная ГЛПР интегральная экспертная оценка ![]() , определенная на целочисленной шкале
, определенная на целочисленной шкале ![]() , где
, где ![]() ,
, ![]() ‑ нижняя и верхняя оценки соответственно. Оценки
‑ нижняя и верхняя оценки соответственно. Оценки ![]() считаем нечеткими, имеющими функции принадлежности
считаем нечеткими, имеющими функции принадлежности ![]() , так что величины
, так что величины ![]() представляют собой ядра нечеткой переменной
представляют собой ядра нечеткой переменной ![]() [9].
[9].
Полагаем, что нормализация оценок ![]() выполнена таким образом, что все оценки
выполнена таким образом, что все оценки ![]() принадлежат интервалу
принадлежат интервалу ![]() ;
; ![]() ;
; ![]() .
.
Значения указанных функций принадлежности, соответствующих формальной оценке ![]() элемента
элемента ![]() , обозначаем
, обозначаем ![]() ,
, ![]() ;
; ![]() . Называем величину
. Называем величину
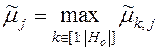 ,
, ![]()
приведенной экспертной оценкой элемента ![]() . Набор этих оценок для всех элементов множества
. Набор этих оценок для всех элементов множества ![]() обозначаем
обозначаем ![]() .
.
Введем меру близости ![]() формальной и приведенной экспертной оценок
формальной и приведенной экспертной оценок ![]() элемента множества
элемента множества ![]() . Определим также меру близости наборов формальных и экспертных оценок всех элементов указанного множества
. Определим также меру близости наборов формальных и экспертных оценок всех элементов указанного множества
![]() .
.
Легко видеть, что эта мера является некоторой функцией весовых коэффициентов ![]() , т.е.
, т.е. ![]() .
.
Таким образом, задача определения оптимального вектора весовых коэффициентов ![]() имеет вид
имеет вид
![]() , (1)
, (1)
где ![]() - параллелепипед допустимых значений компонентов вектора
- параллелепипед допустимых значений компонентов вектора ![]() :
:
![]() .
.
Здесь ![]() ,
, ![]() - заданные константы (не обязательно положительные).
- заданные константы (не обязательно положительные).
2. Метод решения задачи
Общая схема метода интегральной оценки многокритериальных альтернатив имеет следующий вид.
1) Случайным образом выделяем из множества ![]() обучающую
обучающую ![]() и тестовую
и тестовую ![]() выборки таким образом, что
выборки таким образом, что ![]() и
и ![]() .
.
2) На обучающей выборке решаем задачу (1) – определяем компоненты вектора ![]() и соответствующее значение меры
и соответствующее значение меры ![]() .
.
3) С использованием найденных весовых коэффициентов ![]() вычисляем значение
вычисляем значение ![]() той же меры на тестовой выборке.
той же меры на тестовой выборке.
4) Если условие завершения итераций
![]()
выполнено, то завершаем вычисления. В противном случае путем равномерного случайного выбора выделяем из множества ![]() другие обучающую и тестовые выборки и переходим к шагу 2. Здесь
другие обучающую и тестовые выборки и переходим к шагу 2. Здесь ![]() ‑ некоторая мера близости величин
‑ некоторая мера близости величин ![]() ,
, ![]() ,
, ![]() ‑ заданная положительная константа.
‑ заданная положительная константа.
На шаге 2 рассмотренной схемы простым алгоритмом эволюции разума SMEC решаем задачу (1), представляющую собой задачу глобальной условной оптимизации. В алгоритме MEC принято говорить в максимизации целевой функции. Очевидно, что задача минимизации (1) может быть сведена к аналогичной задаче максимизации путем простого инвертирования значений функции ![]() .
.
Мультипопуляция алгоритм MEC состоит из лидирующих групп (superior groups)  и отстающих групп (temporary groups)
и отстающих групп (temporary groups) 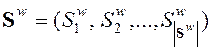 числом
числом ![]() и
и ![]() соответственно. В оригинальном алгоритме MEC числа индивидов в каждой из групп полагают одинаковыми и равными
соответственно. В оригинальном алгоритме MEC числа индивидов в каждой из групп полагают одинаковыми и равными ![]() .
.
Каждая из групп ![]() ,
, ![]() имеет свою коммуникационную среду, которая названа авторами алгоритма локальной доской объявлений (localbillboard). Обозначим эти доски
имеет свою коммуникационную среду, которая названа авторами алгоритма локальной доской объявлений (localbillboard). Обозначим эти доски ![]() ,
, ![]() соответственно. Кроме того, вся мультипопуляция
соответственно. Кроме того, вся мультипопуляция ![]() имеет общую, глобальную доску объявлений (globalbillboard)
имеет общую, глобальную доску объявлений (globalbillboard) ![]() .
.
Если далее в обозначениях групп и соответствующих локальных досок объявлений индексы ![]() опущены, то имеется в виду произвольная из этих групп и их досок объявлений. Размерность такой группы обозначаем
опущены, то имеется в виду произвольная из этих групп и их досок объявлений. Размерность такой группы обозначаем ![]() .
.
Алгоритм SMEC построен на основе операций инициализации групп, локальных состязаний (similar-taxis) и диссимиляции (dissimilation). Поочередно рассмотрим эти операции.
Операция инициализации групп создает группы ![]() ,
, ![]() из
из ![]() индивидов каждая и размещает их в области поиска. Рассмотрим схему операции на примере группы
индивидов каждая и размещает их в области поиска. Рассмотрим схему операции на примере группы ![]() ,
, ![]() .
.
1) Генерируем случайный вектор ![]() , компоненты которого равномерно распределены в области поиска П. Отождествляем этот вектор с индивидом
, компоненты которого равномерно распределены в области поиска П. Отождествляем этот вектор с индивидом ![]() группы
группы ![]() .
.
2) Определяем начальные координаты остальных индивидов данной группы ![]() ,
, ![]() по формуле
по формуле
![]() , (2)
, (2)
то есть размещаем случайным образом вокруг индивида![]() в соответствии с нормальным законом распределения, имеющим по всем
в соответствии с нормальным законом распределения, имеющим по всем ![]() координатам нулевое математическое ожидание и среднее квадратичное отклонение
координатам нулевое математическое ожидание и среднее квадратичное отклонение ![]() (свободный параметр алгоритма).
(свободный параметр алгоритма).
Операция локальных состязаний реализует локальный поиск максимума целевой функции каждой из групп ![]() ,
,![]() ,
, ![]() ,
,![]() . Рассмотрим в качестве примера схему этой операции для группы
. Рассмотрим в качестве примера схему этой операции для группы ![]() .
.
1) С доски объявлений ![]() берем информацию о текущем индивиде-победителе группы
берем информацию о текущем индивиде-победителе группы ![]() . Пусть это будет индивид
. Пусть это будет индивид ![]() ,
, ![]() .
.
2) Определяем новые координаты остальных индивидов ![]() ,
, ![]() ,
, ![]() данной группы по правилу вида (2), т.е. размещаем случайным образом вокруг победителя в соответствии с нормальным законом распределения, среднее квадратичное отклонение которого с ростом числа итераций убывает вследствие умножения на «когнитивную» константу
данной группы по правилу вида (2), т.е. размещаем случайным образом вокруг победителя в соответствии с нормальным законом распределения, среднее квадратичное отклонение которого с ростом числа итераций убывает вследствие умножения на «когнитивную» константу ![]() .
.
3) Вычисляем новые счета (scores)индивидов группы ![]() ,
, ![]() , где
, где ![]() - значение функции
- значение функции ![]() в точке с координатами
в точке с координатами ![]() .
.
4) Определяем нового победителя группы ![]() ,
, ![]() , т.е. индивида данной группы, который имеет максимальный текущий счет:
, т.е. индивида данной группы, который имеет максимальный текущий счет:
 ,
, ![]() .
.
5) Заносим информацию о новом победителе группы ![]() на доски объявлений
на доски объявлений ![]() ,
, ![]() .
.
Операция диссимиляции управляет глобальным поиском. Схема операции имеет следующий вид.
1) С глобальной доски объявлений ![]() считываем счета
считываем счета ![]() ,
, ![]() ,
, ![]() ,
,![]() всех групп (т.е. текущие счета победителей этих групп).
всех групп (т.е. текущие счета победителей этих групп).
2) Выполняем сравнение указанных счетов между собой. Если счет некоторой лидирующей группы ![]() меньше счета одной из отстающих групп
меньше счета одной из отстающих групп ![]() , то последняя группа занимает место группы
, то последняя группа занимает место группы ![]() во множестве лидирующих групп, а группа
во множестве лидирующих групп, а группа ![]() ‑ место группы
‑ место группы ![]() среди отстающих групп. Если счет группы
среди отстающих групп. Если счет группы ![]() ниже счетов всех лидирующих групп, то удаляем группу
ниже счетов всех лидирующих групп, то удаляем группу ![]() из популяции.
из популяции.
3) С помощью операции инициализации взамен каждой из удаленных групп инициализируем новую группу.
Операции локальных состязаний и диссимиляции итерационно повторяем до тех пор, пока имеет место увеличение максимального счета лидирующих групп. При отсутствии роста этого счета в течение ![]() итераций (критерий стагнации вычислений), решение задачи, соответствующее победителю лучшей из лидирующих групп, объявляем точкой глобального экстремума.
итераций (критерий стагнации вычислений), решение задачи, соответствующее победителю лучшей из лидирующих групп, объявляем точкой глобального экстремума.
Учет ограничений ![]() на варьируемые параметры во всех случаях производим, так называемым, методом смертельных штрафов, когда недопустимые значения компонентов вектора
на варьируемые параметры во всех случаях производим, так называемым, методом смертельных штрафов, когда недопустимые значения компонентов вектора ![]() просто отвергаются.
просто отвергаются.
3. Программная реализация метода
Реализация метода выполнена на языке программирования Pythonс использованием библиотек matplotlob, numpy, scipy, os.Соответствующая программа получила наименование MEC-Python. Язык программирования Pythonявляется высокоуровневым интерпретируемым языком программирования, включающим, широкий спектр функций, интегрированную среду разработки и объектно-ориентированные возможности.
Основные входными данные программы MEC-Pythonразбиты на три группы, условно названные данные задачи, данные метода, данные алгоритма.
К входным данным задачи отнесены
‑ число частных критериев оптимальности ![]() ,
,
‑ тип используемой скалярной свертки (выбирается пользователем из библиотеки сверток),
‑ число элементов ![]() во множестве
во множестве ![]() , а также числа элементов
, а также числа элементов ![]() в обучающей и тестовой выборках,
в обучающей и тестовой выборках,
‑ шкалы ![]() (используются только с целью проверки корректности исходных данных программы),
(используются только с целью проверки корректности исходных данных программы),
‑ имя файла, содержащего набор ![]() формальных оценок всех элементов множества
формальных оценок всех элементов множества ![]() , а также соответствующих интегральных экспертных оценок
, а также соответствующих интегральных экспертных оценок ![]() ,
,
‑ функции принадлежности ![]() (выбирается пользователем из библиотеки этих функций),
(выбирается пользователем из библиотеки этих функций),
‑ мера близости ![]() формальной и приведенной экспертной оценок (выбирается пользователем из соответствующей библиотеки),
формальной и приведенной экспертной оценок (выбирается пользователем из соответствующей библиотеки),
‑ мера близости ![]() наборов формальных и экспертных оценок (выбирается пользователем из библиотеки этих мер),
наборов формальных и экспертных оценок (выбирается пользователем из библиотеки этих мер),
‑ константы ![]() ,
, ![]() ,
, ![]() , определяющие параллелепипед П допустимых значений компонентов вектора
, определяющие параллелепипед П допустимых значений компонентов вектора ![]() .
.
В библиотеке скалярных сверток содержится аддитивная свертка
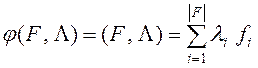 , (3)
, (3)
мультипликативная свертка

и свертка Гермейера
 .
.
Библиотека функций принадлежности включает в себя функции классов ![]() [10].
[10].
Библиотека мер близости оценок (формальной ![]() и приведенной экспертной
и приведенной экспертной ![]() ) включает в себя только модуль разности указанных оценок:
) включает в себя только модуль разности указанных оценок:
![]() . (4)
. (4)
Библиотека мер близости наборов формальных и экспертных оценок содержит гарантирующую меру
![]() , (5)
, (5)
срединную меру

и евклидову меру
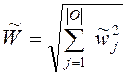 .
.
Входные данные метода включают в себя
‑ меру ![]() (выбирается пользователем из библиотеки этих мер),
(выбирается пользователем из библиотеки этих мер),
‑ константу ![]() ,
,
‑ максимально допустимое число итераций ![]() .
.
Библиотека мер включает в себя меру
![]() . (6)
. (6)
Все указанные библиотеки могут быть расширены пользователем путем добавления в них соответствующих Python-функций.
Входные данные алгоритма представляют собой свободные параметры алгоритма SMEC:
‑ число групп ![]() ;
;
‑ число индивидов в группе ![]() ;
;
‑ среднее квадратичное отклонение ![]() , используемое в операциях инициализации групп и локальных состязаний индивидов;
, используемое в операциях инициализации групп и локальных состязаний индивидов;
‑ максимально допустимое число итераций алгоритма ![]() ;
;
‑ критерий стагнации алгоритма ![]() ;
;
‑ константа стагнации ![]() ;
;
‑ число мультистартов ![]() .
.
Выходными данными программы являются оптимальные значения весовых коэффициентов ![]() , а также приведенные экспертные оценки
, а также приведенные экспертные оценки ![]() элемента
элемента ![]() ,
, ![]() .
.
4. Исследование эффективности алгоритма MEC
Исследование выполнено для одноэкстремальной, но овражной функции Розенброка (Rozenbrock)
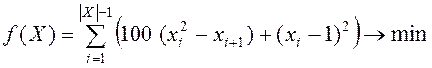 ,
,
минимальное значение ![]() которой достигается в точке с координатами
которой достигается в точке с координатами ![]() и равно нулю, а также для многоэкстремальной функции функция Растригина (Rastrigin)
и равно нулю, а также для многоэкстремальной функции функция Растригина (Rastrigin)
 ,
,
глобальный минимум которой ![]() также достигается в точке
также достигается в точке ![]() . В обоих случаях задачу глобальной оптимизации решаем в области
. В обоих случаях задачу глобальной оптимизации решаем в области ![]() .
.
В качестве критерия эффективности алгоритма используем близость найденного с его помощью решения ![]() к точному решению
к точному решению ![]() . Поскольку для рассматриваемых функций
. Поскольку для рассматриваемых функций ![]() , мерой эффективности алгоритма является величина
, мерой эффективности алгоритма является величина ![]() .
.
Одной из целей исследования было изучения влияния следующих значений свободных параметров на эффективность алгоритма:
‑ размерность задачи ![]() (варианты
(варианты ![]() ),
),
‑ число групп ![]() =10; 20; 30.
=10; 20; 30.
‑ число индивидов в группе ![]() =10; 20; 30,
=10; 20; 30,
‑ когнитивный параметр ![]() =0,7; 0,8; 0,9.
=0,7; 0,8; 0,9.
Во всех случаях использовано значение константы стагнации ![]() .
.
Сводные результаты исследования для функции Розенброка представлены в таблице 1.
Таблица 1 – Результаты исследования эффективности алгоритма MEC: функция Розенброка
|
|
|
10; 10; 0,7 | 2 | 1,404 e-007 |
4 | 0,0191 | |
8 | 0,1396 | |
16 | 7,3340 | |
10; 10; 0,8 | 2 | 3,2159 e-007 |
4 | 0,0009 | |
8 | 0,5252 | |
16 | 2,8800 | |
10; 10; 0,9 | 2 | 1,7120 e-008 |
4 | 0,0011 | |
8 | 0,3095 | |
16 | 2,5297 | |
20, 20, 07 | 2 | 9,5511 e-009 |
4 | 0,0026 | |
8 | 0,7198 | |
16 | 3,6943 | |
20; 20; 0,8 | 2 | 5,5208 e-009 |
4 | 0,0018 | |
8 | 0,2302 | |
16 | 1,8081 | |
20; 20; 0,9 | 2 | 8,8357 e-010 |
4 | 0,0109 | |
8 | 0,2852 | |
16 | 0,5709 | |
30; 30; 0,7 | 2 | 3,1744 e-008 |
4 | 0,0024 | |
8 | 0,1803 | |
16 | 2,8831 | |
30; 30; 0,8 | 2 | 1,4891 e-009 |
4 | 1,1577 e-005 | |
8 | 0,5455 | |
16 | 0,6972 | |
30; 30; 0,9 | 2 | 4,7989 e-008 |
4 | 0,0001 | |
8 | 0,1316 | |
16 | 1,2898 |
Характер сходимости итераций при поиске минимума функции Розенброка иллюстрируют рисунки 1 ‑ 3. Здесь и далее нижняя кривая соответствует ![]() , следующая кривая ‑
, следующая кривая ‑ ![]() , третья снизу кривая ‑
, третья снизу кривая ‑ ![]() , последняя кривая ‑
, последняя кривая ‑ ![]() . Величина
. Величина ![]() представляет собой номер итерации.
представляет собой номер итерации.
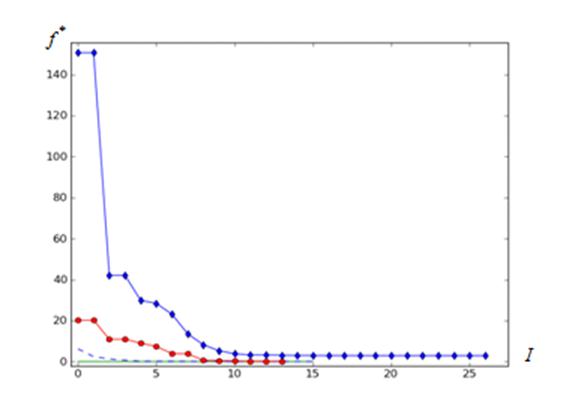
Рисунок 1 – Сходимость алгоритма: функция Розенброка; ![]() =
=![]() ;
; ![]()

Рисунок 2 – Сходимость алгоритма: функция Розенброка; ![]() =
=![]() ;
; ![]()
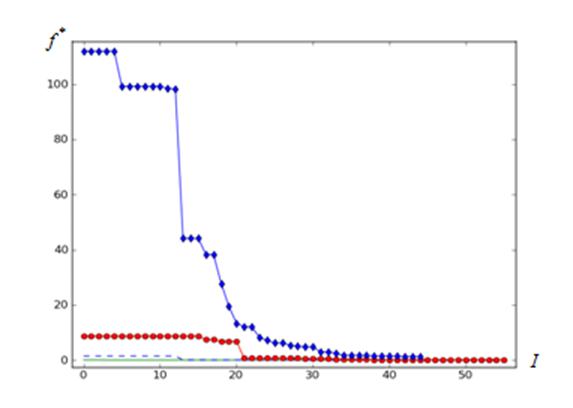
Рисунок 3 – Сходимость алгоритма: функция Розенброка; ![]() =
=![]() ;
; ![]()
Сводные результаты для функции Растригина представлены в таблице 2, которую иллюстрируют рисунки 4 – 6. Здесь ![]() - номер итерации.
- номер итерации.
Таблица 1 – Результаты исследования эффективности алгоритма MEC: функция Растригина
|
|
|
10; 10; 0,7 | 2 | 8.8947 e-006 |
4 | 0.0005 | |
8 | 3.3385 | |
16 | 37.6244 | |
10; 10; 0,8 | 2 | 4.07180 e-005 |
4 | 0.0004 | |
8 | 2.01036 | |
16 | 16.6754402773 | |
10; 10; 0,9 | 2 | 0.0001 |
4 | 0.0024 | |
8 | 0.9976 | |
16 | 4.44030 | |
20; 20; 0,7 | 2 | 2.5025 e-007 |
4 | 0.0005 | |
8 | 1.0070 | |
16 | 10.7573 | |
20; 20; 0,8 | 2 | 8.2661 e-006 |
4 | 0.0001 | |
8 | 1.9907 | |
16 | 6.2998 | |
20; 20; 0,9 | 2 | 1.6857 e-005 |
4 | 0.0005 | |
8 | 2.9862 | |
16 | 4.9775 | |
30; 30; 0,7 | 2 | 1.4032 e-006 |
4 | 2.0638 e-005 | |
8 | 1.0041 | |
16 | 7.9626 | |
30; 30; 0,8 | 2 | 5.4772 e-006 |
4 | 0.0005 | |
8 | 1.9914 | |
16 | 6.3869 | |
30; 30; 0,9 | 2 | 2.7111 e-005 |
4 | 0.0015 | |
8 | 2.9858 | |
16 | 5.9760 |

Рисунок 4 – Сходимость алгоритма: функция Растригина; ![]() =
=![]() ;
; ![]()
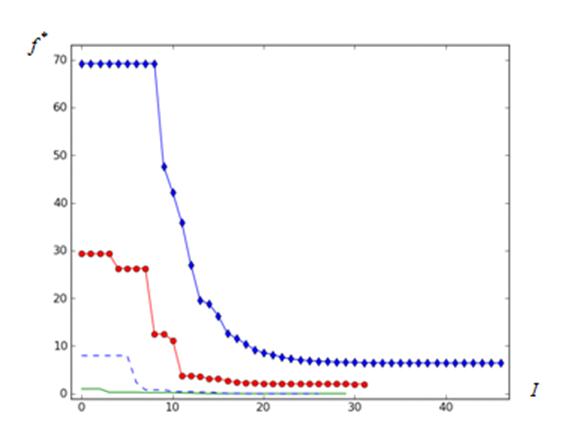
Рисунок 5 – Сходимость алгоритма: функция Растригина; ![]() =
=![]() ;
; ![]()
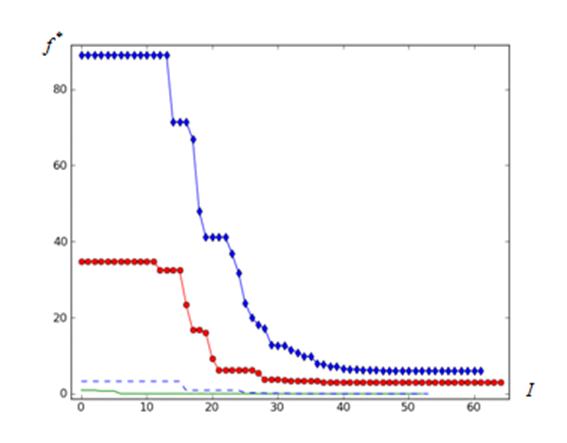
Рисунок 6 – Сходимость алгоритма: функция Растригина; ![]() =
=![]() ;
; ![]()
Результаты исследования показывают, что в случае высокой размерности пространства поиска для обеспечения локализации минимума целевой функции с приемлемой точностью нужно использовать большие числа групп и индивидов в них. Результаты показывают также сильную зависимость достигнутой точности локализации от величины когнитивного параметра ![]() . Данный факт обусловлен тем, что при
. Данный факт обусловлен тем, что при ![]() повышаются диверсификационные свойства алгоритма, так что стагнация наблюдается позже.
повышаются диверсификационные свойства алгоритма, так что стагнация наблюдается позже.
5. Вычислительный эксперимент
С использованием программы MEC-Pythonвыполнено два вычислительных эксперимента. Во всех случаях использованы следующие значения основных входных данных.
Входные данные задачи:
‑ скалярная аддитивная свертка (3);
‑ пятибалльные шкалы ![]() ;
;
‑ гауссовы функции принадлежности с ядрами ![]() и средним квадратичным отклонением 0,2821;
и средним квадратичным отклонением 0,2821;
‑ мера близости ![]() формальной и приведенной экспертной оценок (4);
формальной и приведенной экспертной оценок (4);
‑ мера близости ![]() наборов формальных и экспертных оценок (5),
наборов формальных и экспертных оценок (5),
‑ константы ![]() ,
, ![]() ;
; ![]() .
.
Входные данные метода:
‑ мера (6);
‑ константа ![]() ;
;
‑ максимально допустимое число итераций ![]() .
.
Входные данные алгоритма:
‑ число групп ![]() ;
;
‑ число индивидов в группе ![]() ;
;
‑ среднее квадратичное отклонение ![]() ;
;
‑ максимально допустимое число итераций алгоритма ![]() ;
;
‑ критерий стагнации алгоритма ![]() ;
;
‑ константа стагнации ![]() ;
;
‑ число мультистартов ![]() ;
;
‑ когнитивный параметр ![]() .
.
Эксперимент 1![]() выполнен с целью тестирования метода и его программной реализации. Мощность множества
выполнен с целью тестирования метода и его программной реализации. Мощность множества ![]() в эксперименте прията равной
в эксперименте прията равной ![]() , а мощность обучающей и тестовой выборок равной
, а мощность обучающей и тестовой выборок равной ![]() соответственно. Набор формальных оценок
соответственно. Набор формальных оценок ![]() элементов множества
элементов множества ![]() , а также набор соответствующих интегральных экспертных оценок
, а также набор соответствующих интегральных экспертных оценок ![]() (таблица 1) получены по следующей схеме:
(таблица 1) получены по следующей схеме:
‑ генерируем для данного элемента ![]() ,
, ![]() случайную экспертную оценку
случайную экспертную оценку ![]() , равномерно распределенную на дискретном множестве
, равномерно распределенную на дискретном множестве ![]() ;
;
‑ генерируем случайные величины ![]() ,распределенные по нормальному закону с математическим ожиданием, равным
,распределенные по нормальному закону с математическим ожиданием, равным ![]() , и средним квадратичным отклонением, равным 1,22;
, и средним квадратичным отклонением, равным 1,22;
‑ величины ![]() получаем путем округления по математическим правилам величин
получаем путем округления по математическим правилам величин ![]() .
.
Вычисленные программой приведенные экспертные оценки ![]() , а также невязки
, а также невязки ![]() также представлены в таблице 3. Найденные оптимальные значения весовых множителей приведены в таблице 4. Таблицу 3 иллюстрирует рисунок 7, на котором представлена гистограмма невязок
также представлены в таблице 3. Найденные оптимальные значения весовых множителей приведены в таблице 4. Таблицу 3 иллюстрирует рисунок 7, на котором представлена гистограмма невязок ![]() .
.
Результаты эксперимента 1 показывают работоспособность метода и его программного обеспечения.
Таблица 3 – Исходные и результирующие оценки: эксперимент 1
j |
|
|
|
|
|
|
|
|
1 | 3 | 4 | 5 | 3 | 3 | 4 | 3,94 | 0,06 |
2 | 5 | 3 | 5 | 3 | 2 | 4 | 3,11 | 0,89 |
3 | 4 | 5 | 4 | 2 | 3 | 3 | 3,86 | 0,86 |
4 | 3 | 4 | 5 | 3 | 4 | 5 | 4,97 | 0,03 |
5 | 4 | 5 | 3 | 5 | 4 | 4 | 3,99 | 0,01 |
6 | 5 | 2 | 2 | 5 | 4 | 5 | 3,94 | 1,06 |
7 | 2 | 2 | 3 | 4 | 2 | 2 | 2,15 | 0,15 |
8 | 2 | 3 | 2 | 4 | 3 | 3 | 2,83 | 0,17 |
9 | 2 | 5 | 4 | 4 | 2 | 2 | 2,27 | 0,27 |
10 | 4 | 3 | 2 | 3 | 2 | 2 | 2,15 | 0,15 |
11 | 3 | 3 | 2 | 4 | 5 | 5 | 4,97 | 0,03 |
12 | 4 | 2 | 2 | 4 | 2 | 2 | 2,00 | 0 |
13 | 3 | 3 | 2 | 4 | 5 | 5 | 4,97 | 0,03 |
14 | 3 | 5 | 4 | 5 | 4 | 3 | 4,20 | 1,2 |
15 | 4 | 5 | 4 | 5 | 2 | 3 | 2,21 | 0,79 |
16 | 4 | 3 | 5 | 2 | 2 | 3 | 3,24 | 0,76 |
17 | 4 | 2 | 3 | 5 | 2 | 2 | 2,08 | 0,08 |
18 | 3 | 3 | 2 | 3 | 5 | 5 | 5,18 | 0,18 |
19 | 2 | 2 | 3 | 4 | 2 | 2 | 2,15 | 0,15 |
20 | 3 | 3 | 2 | 2 | 2 | 2 | 2,28 | 0,28 |
Таблица 4 – Оптимальные значения весовых множителей: эксперимент 1
|
|
|
|
|
0,074 | -0,058 | 0,293 | -0,207 | 1,033 |
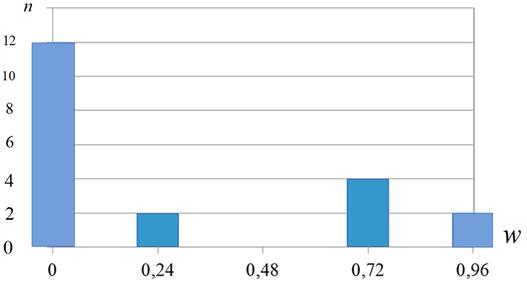
Рисунок 7 – Гистограмма невязок ![]() : эксперимент 1
: эксперимент 1
Эксперимент 2 выполнен в рамках апробации ментально-структурированной образовательной технологии [1, 11]. В эксперименте использованы количественные показатели качества образовательного процесса в ВУЗе, полученные, в частности, с помощью системы автоматизированного анализа структурированных электронных документов [12]. Точнее говоря, использованы следующие показатели качества расчетно-пояснительной записки (РПЗ) к курсовой работе по дисциплине «Технология программирования» тринадцати студентов одной из учебных групп второго курса МГТУ им. Н.Э. Баумана: ![]() ‑ новизна,
‑ новизна, ![]() ‑ трудоемкость,
‑ трудоемкость, ![]() ‑ сложность,
‑ сложность, ![]() ‑ системность,
‑ системность, ![]() ‑ структурированность.
‑ структурированность.
Новизна работы ![]() оценивалась на основании того, какая часть (в процентном отношении) от общего объема понятийного тезауруса указанной учебной дисциплины использована студентом в его РПЗ. Трудоемкость работы
оценивалась на основании того, какая часть (в процентном отношении) от общего объема понятийного тезауруса указанной учебной дисциплины использована студентом в его РПЗ. Трудоемкость работы ![]() получена на основе количества времени, которое студент потратил на формирование своей РПЗ, и объема РПЗ, измеренного числом знаков в документе. Указанные величины формируют современные редакторы документов, например, в MicrosoftWord. Для оценки сложность работы
получена на основе количества времени, которое студент потратил на формирование своей РПЗ, и объема РПЗ, измеренного числом знаков в документе. Указанные величины формируют современные редакторы документов, например, в MicrosoftWord. Для оценки сложность работы ![]() использована колмогоровская сложность файла, содержащего РПЗ, как количественная мера информации, заключенной работе. В качестве меры системности работы
использована колмогоровская сложность файла, содержащего РПЗ, как количественная мера информации, заключенной работе. В качестве меры системности работы ![]() использована связность семантической сети соответствующей РПЗ. Наконец, структурированность работы
использована связность семантической сети соответствующей РПЗ. Наконец, структурированность работы ![]() оценивалась с помощью нормированного интегрального показателя, построенного на основе чисел разделов, рисунков, таблиц, формул и библиографических источников в РПЗ.
оценивалась с помощью нормированного интегрального показателя, построенного на основе чисел разделов, рисунков, таблиц, формул и библиографических источников в РПЗ.
Итого, в эксперименте 2 мощности множеств ![]() приняты равными
приняты равными ![]() соответственно, число частных критериев оптимальности
соответственно, число частных критериев оптимальности ![]() . Наборы исходных формальных и соответствующих интегральных экспертных оценок представлены в таблице 5. Те же нормализованные данные приведены в таблице 6.
. Наборы исходных формальных и соответствующих интегральных экспертных оценок представлены в таблице 5. Те же нормализованные данные приведены в таблице 6.
Таблица 5 ‑ Исходные оценки: эксперимент 2
|
|
|
|
|
|
|
1 | 0 | 0 | 53,79 | 108 | 20 | 4 |
2 | 7,70 | 35,8 | 52,34 | 142 | 24 | 5 |
3 | 9,62 | 24,83 | 8,53 | 199 | 24 | 5 |
4 | 7,69 | 34,80 | 13,74 | 128 | 26 | 5 |
5 | 0 | 46,04 | 146,46 | 166 | 22 | 5 |
6 | 3,85 | 24,08 | 60,19 | 143 | 17 | 5 |
7 | 3,85 | 30,00 | 45,36 | 152 | 14 | 5 |
8 | 3,85 | 46,04 | 53,79 | 162 | 32 | 5 |
9 | 7,69 | 28,72 | 3,37 | 139 | 7 | 5 |
10 | 3,85 | 237,57 | 5,43 | 96 | 18 | 3 |
11 | 5,77 | 21,12 | 68,20 | 201 | 25 | 5 |
12 | 5,77 | 68,24 | 31,88 | 144 | 25 | 5 |
13 | 1,79 | 73,60 | 21,18 | 112 | 21 | 4 |
Таблица 6 – Нормализованные входные данные: эксперимент 2
j |
|
|
|
|
|
|
|
1 | 4 | 2,00 | 5,00 | 3,95 | 2,68 | 3,13 | 4 |
2 | 5 | 4,01 | 4,25 | 3,84 | 3,53 | 3,75 | 5 |
3 | 5 | 5,00 | 4,48 | 2,00 | 4,95 | 3,75 | 5 |
4 | 5 | 3,99 | 4,26 | 2,00 | 3,18 | 4,06 | 5 |
5 | 5 | 2,00 | 4,03 | 5,00 | 4,13 | 3,44 | 5 |
6 | 5 | 2,00 | 4,49 | 4,43 | 3,56 | 2,66 | 5 |
7 | 5 | 2,00 | 4,36 | 3,34 | 3,78 | 2,19 | 5 |
8 | 5 | 2,00 | 4,03 | 3,96 | 4,03 | 5,00 | 5 |
9 | 5 | 3,99 | 4,39 | 2,00 | 3,48 | 2,00 | 5 |
10 | 3 | 2,00 | 2,00 | 2,00 | 2,39 | 2,81 | 3 |
11 | 5 | 2,99 | 4,56 | 5,00 | 5,00 | 3,91 | 5 |
12 | 5 | 2,99 | 3,56 | 2,00 | 4,00 | 3,91 | 5 |
13 | 4 | 2,00 | 3,45 | 2,00 | 2,79 | 3,28 | 4 |
Результаты работы программы представлены в таблицах 7, 8. Таблицу 7 иллюстрирует рисунок 8, аналогичный рисунку 7.
Таблица 7– Исходные и результирующие оценки: эксперимент 2
j |
|
|
|
1 | 4 | 3,23 | 0,77 |
2 | 5 | 4,86 | 0,14 |
3 | 5 | 4,73 | 0,27 |
4 | 5 | 4,85 | 0,15 |
5 | 5 | 4,15 | 0,85 |
6 | 5 | 3,35 | 1,65 |
7 | 5 | 2,42 | 2,58 |
8 | 5 | 4,73 | 0,27 |
9 | 5 | 2,98 | 2,02 |
10 | 3 | 3,75 | 0,75 |
11 | 5 | 4,59 | 0,41 |
12 | 5 | 4,31 | 0,69 |
13 | 4 | 3,28 | 0,72 |
Таблица 8 – Оптимальные значения весовых множителей: эксперимент 2
|
|
|
|
|
0,30 | -0,19 | 0,24 | -0,17 | 1,05 |
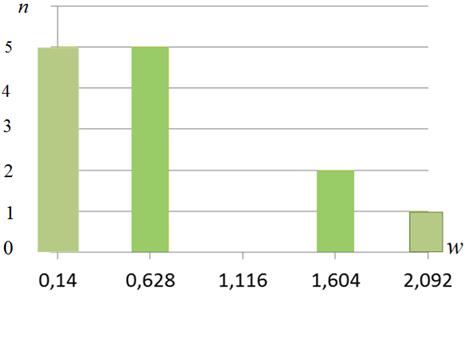
Рисунок 8 – Гистограмма невязок ![]() : эксперимент 2
: эксперимент 2
Заключение
В работе предложен метод получения интегральных оценок многокритериальных альтернатив в ментально-структурированном походе к обучению. Метод предполагает сведение задачи получения указанных оценок к задаче глобальной условной оптимизации. Для решения данной задачи предложено использовать алгоритм эволюции разума MEC, как один из относительно новых и перспективных алгоритмов глобальной оптимизации.
На языке программирования Pythonразработана программа, реализующая предложенный метод получения интегральных оценок. С помощью данной программы выполнено исследование эффективности метода и его программной реализации. Вычислительные эксперименты показали эффективность принятых алгоритмических и программных решений.
Работа выполнена в рамках Государственного контракта № 16.740.11.0407 от 26 ноября 2010 г.
Литература
1. Добряков А.А., Карпенко А.М., Смирнова Е.В. Основные принципы ментально-структурированной образовательной технологии, ориентированные на формирование компетентности специалиста технического профиля // Наука и образование: электронное научно- техническое издание, 2011, № 10 (http://technomag.edu.ru/doc/237464.html).
2. Черноруцкий И.Г. Методы принятия решений. – СПб.: БХВ-Петербург, 2005.- 416 с.
3. Карпенко А.П., Федорук В.Г. Один класс прямых адаптивных методов многокритериальной оптимизации // Информационные технологии.- 2009.- №5.- С. 24-30.
4. Орлянская И.В. Современные подходы к построению методов глобальной оптимизации // Электронный журнал «Исследовано в России» (http://zhurnal.ape.relarn.ru/articles/2002/189.pdf).
5. Engelbrecht A. P. Computational Intelligence. An Introduction (second edition).- John Wiley & Sons, 2007. - 597 p.
6. Jie J., Han Ch., Zeng J. An Extended Mind Evolutionary Computation Model for Optimizations // Applied Mathematics and Computation, 2007, No. 185(2), pp. 1038 – 1049.
7. Jie J., Zeng J. Improved mind evolutionary computation for optimizations / Proceedings of the 5th World Congress on Intelligent Control and Automation, WCICA 2004, Hangzhou, China 3, Vol. 3, pp. 2200-2204.
8. Lui J., Li N., Xie K. Application of Chaos Mind Evolutionary Algorithm in Antenna Arrays Synthesis // Journal of computers, 2010, Vol. 5, No. 5, pp. 717-724.
9. Штовба С.Д. Введение в теорию нечетких множеств и нечеткую логику / С.Д. Штовба.- Режим доступа: http//www.matlab.exponenta.ru, свободный.
10. Д. Рутковская, М. Пилиньский, Л. Рутковский. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польского И. Д. Рудинского. — М.:Горячая линия — Телеком, 2004. — 452 с.
11. Галямова Е.В., Карпенко А.П., Соколов Н.К. Методика контроля понятийных знаний субъекта обучения в обучающей системе /Наука и образование: электронное научно-техническое издание, 2009, 2, 042090025\0007 (http://technomag.edu.ru/doc/115086.html )
12. Смирнова Е.В., Панов А.С. Система автоматического анализа структурированного электронного документа / Свидетельство о государственной регистрации Программы для ЭВМ № 2011615171 от 01 июля 2011 г.
Публикации с ключевыми словами: многокритериальное принятие решений, задача глобальной условной многомерной оптимизации, алгоритм эволюции разума
Публикации со словами: многокритериальное принятие решений, задача глобальной условной многомерной оптимизации, алгоритм эволюции разума
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



