научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2012
УДК 519.216.1/2
МГТУ им. Н.Э. Баумана
Вычислительная и функциональная эффективность решения многих задач цифровой обработки сигналов спектральными методами существенно зависит от используемых систем базисных функций [1]. Поскольку ортогональных систем базисных функций существует неограниченное множество, то выбор рационального базиса является сложной теоретической и прикладной проблемой. В этих условиях особенно полезными могут оказаться параметрические базисные функции, содержащие в своей структуре один или несколько изменяемых параметров, влияющих на их свойства. Известным и важным примером таких базисов служит класс комплексных экспоненциальных функций Виленкина-Крестенсона [2], управление свойствами которых осуществляется с помощью вариации основания используемой системы счисления. Обобщение этих функций на многоосновную систему счисления (систему счисления с переменным основанием) и применение дополнительных способов их переупорядочения значительно расширяет ассортимент возможных базисных систем, среди которых можно искать базис, в наибольшей степени удовлетворяющий условию решаемой задачи обработки. В данной статье рассмотрены известные и новые методы формирования таких базисных систем и их основные свойства, а также оригинальные скалярные алгоритмы быстрого преобразования Фурье на их основе.
Пусть ![]() есть целые положительные числа, принятые в качестве оснований системы счисления, и целые числа k и i, задающие номер и аргумент обобщенной функции Крестенсона (ОФК) W(k, i), на интервале
есть целые положительные числа, принятые в качестве оснований системы счисления, и целые числа k и i, задающие номер и аргумент обобщенной функции Крестенсона (ОФК) W(k, i), на интервале ![]() записаны в виде
записаны в виде
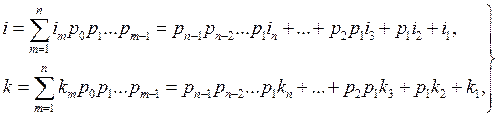 (1)
(1)
где ![]() , а
, а ![]() и
и ![]() являются m-ми разрядами позиционного представления чисел i и k (
являются m-ми разрядами позиционного представления чисел i и k (![]() и
и ![]() - младшие разряды) и лежат в диапазоне
- младшие разряды) и лежат в диапазоне ![]() .
.
Тогда ОФК можно представить следующим выражением [3]:
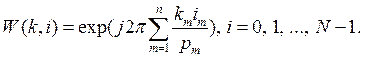 (2)
(2)
где ![]() . Эти функции можно выразить и через произведение дискретных комплексных экспоненциальных функций (ДЭФ)
. Эти функции можно выразить и через произведение дискретных комплексных экспоненциальных функций (ДЭФ) 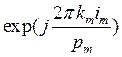 :
:
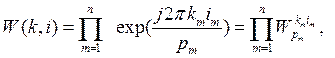
![]() (3)
(3)
где принято 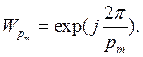
Записанные таким образом ОФК обладают рядом интересных свойств. Приведем основные из них.
1. ОФК являются комплексными функциями с единичным модулем и фазой 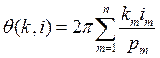 . Вычитая из фазы целое число
. Вычитая из фазы целое число ![]() , можно получить ОФК с минимальными фазами.
, можно получить ОФК с минимальными фазами.
2. В ОФК переменные k и iравноправны, поэтому, если поменять их местами, функция не изменится, т.е.
![]() (4)
(4)
В этом проявляется свойство двойственности ОФК относительно своих аргументов, которое приводит к симметричности матрицы значений ОФК.
3. Среднее значение любой ОФК, кроме нулевой, равно нулю, т.е.
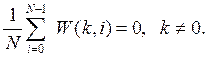 (5)
(5)
Действительно,
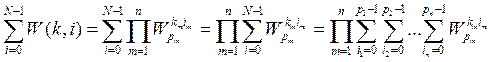 . (6)
. (6)
Но при ![]()
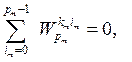
поэтому при ![]() , когда хотя бы один разряд
, когда хотя бы один разряд ![]() , все произведение (6) будет равно нулю. Следовательно, выражение (5) справедливо.
, все произведение (6) будет равно нулю. Следовательно, выражение (5) справедливо.
Среднее значение нулевой ОФК равно единице, т.к. ![]() и
и
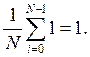
4. Произведение двух любых ОФК дает другую ОФК:
![]() (7)
(7)
где
![]() (8)
(8)
а произведение двух любых ОФК, одна из которых является комплексно-сопряженной, так же принадлежит ОФК:
![]() (9)
(9)
где
![]() (10)
(10)
В выражениях (8) и (10) ![]() и
и ![]() означают операции поразрядного модулярного сложения и вычитания, выполняемые по правилам:
означают операции поразрядного модулярного сложения и вычитания, выполняемые по правилам:
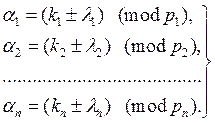 (11)
(11)
Доказательство первого утверждения вытекает из следующих соотношений:
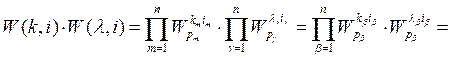
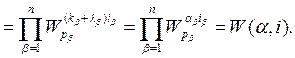
Вывод второго утверждения можно получить аналогичным образом, если учесть, что
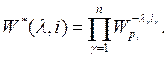
Данное свойство отражает мультипликативность ОФК. В силу своей двойственности ОФК обладают мультипликативностью как по индексу k, так и по индексу i, т.е. являются дважды мультипликативными функциями.
5. Мощность любой ОФК равна 1:
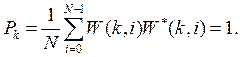 (12)
(12)
Действительно, ![]() и поэтому формула (12) справедлива.
и поэтому формула (12) справедлива.
6. ОФК являются ортогональными функциями, т.к.
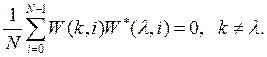 (13)
(13)
Для доказательства этого свойства сначала воспользуемся свойством мультипликативности в виде (9) и запишем сумму в (13) так:
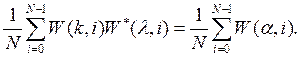
Из этого выражения следует, что взаимная мощность двух ОФК с номерами k и λ равна среднему значению ОФК с номером α, определяемым соотношением (10). Но при ![]() номер
номер ![]() не равен нулю и среднее значение такой ОФК будет равно нулю (см. (5)).
не равен нулю и среднее значение такой ОФК будет равно нулю (см. (5)).
7. Система из N ОФК будет полной системой на интервале [0, N). Это следует из того, что в этом случае к системе нельзя будет добавить ни одной новой функции, которая была бы ортогональной одновременно ко всем остальным функциям системы.
Таким образом, N ОФК образуют полную ортонормированную мультипликативную комплексную дискретную базисную систему ![]() , пригодную для спектрального представления любых решетчатых сигналов ограниченной мощности. Пара ДПФ в базисе ОФК
, пригодную для спектрального представления любых решетчатых сигналов ограниченной мощности. Пара ДПФ в базисе ОФК
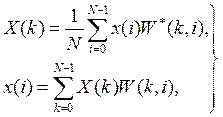 (14)
(14)
а равенство Парсеваля
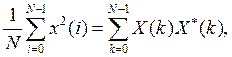 (15)
(15)
где ![]() - комплексно-сопряженная к
- комплексно-сопряженная к ![]() величина.
величина.
Так как ОФК являются дважды мультипликативными функциями, то для их спектров справедливы все общие свойства, приведенные в работе [2]. В частности, выполняются теоремы о модуляции, сдвиге, свертке, корреляции и умножении сигналов. При этом, поскольку операция мультипликативности совпадает с операцией поразрядного сложения или вычитания по переменным модулям, то и операция обобщенного сдвига в этом базисе понимается в этом же смысле. Такие же операции должны быть использованы здесь и при записи обобщенных сверток и корреляций. Энергетические спектры в базисе ОФК инвариантны к такому обобщенному сдвигу.
ДПФ в базисе ОФК можно записать и в матричной форме.
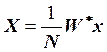 ,
,
![]() ,
,
где матрицы прямых (![]() ) и комплексно спряженных (
) и комплексно спряженных (![]() ) значений ОФК имеют вид:
) значений ОФК имеют вид:
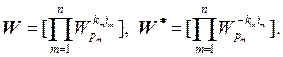
Эти матрицы значений ОФК являются матрицами с полными фазами. Вычитая в них из степеней Wчисла, кратные ![]() , получим матрицы значений с минимальными фазами. Матрицы значений ОФК
, получим матрицы значений с минимальными фазами. Матрицы значений ОФК ![]() и
и ![]() будут симметрическими и унитарными. Они содержат действительные и комплексные элементы, причем комплексные попарно сопряжены. Нулевая строка и нулевой столбец этих матриц состоят только из единичных элементов.
будут симметрическими и унитарными. Они содержат действительные и комплексные элементы, причем комплексные попарно сопряжены. Нулевая строка и нулевой столбец этих матриц состоят только из единичных элементов.
Для ОФК по аналогии с функциями Виленкина-Крестенсона (ВКФ) и функциями Уолша [2] можно вести понятие ранга R, равного числу ненулевых разрядов кода номера функции k. Номер k функции или спектра ранга r можно тогда обозначить в виде ![]() . При r =1 в разложении kбудет только один значащий разряд. Совокупность таких номеров можно записать так:
. При r =1 в разложении kбудет только один значащий разряд. Совокупность таких номеров можно записать так:
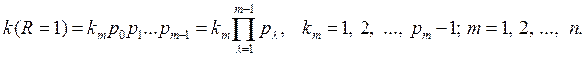
Так как здесь используется только одна переменная с индексом, то ее можно заменить на простую переменную µ и тем самым упростить запись:
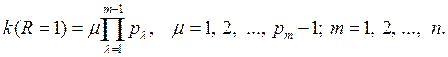
Если значение µ (или km) равно 1, то номер 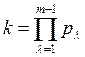 и принадлежит следующему множеству значений:
и принадлежит следующему множеству значений: ![]() . Соответствующие ему функции
. Соответствующие ему функции
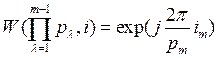 (16)
(16)
и зависят только от значения своего аргумента. Таким свойством обладали обычные функции Радемахера в системах Уолша и обобщенные функции Радемахера в системах ВКФ [2]. По аналогии эти функции так же можно считать обобщенными функциями Радемахера ![]() для системы счисления с переменным основанием. Тогда
для системы счисления с переменным основанием. Тогда
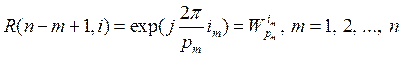 . (17)
. (17)
При введении обозначения функции Радемахера учтено, что с увеличением ее номера число точек изменения ее значений должно возрастать. Очевидно, что в полной системе ОФК (2) содержится только n обобщенных функций Радемахера и любая ОФК (2) может быть выражена через их произведение:
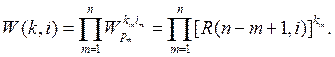 (18)
(18)
Пример 1. Построить систему ОФК для N=6 прямым методом и с помощью функций Радемахера.
Решение. В этом случае ![]() . Поэтому примем
. Поэтому примем ![]() а
а ![]() . Тогда числа k и i запишутся в виде
. Тогда числа k и i запишутся в виде ![]() и
и ![]() , где
, где ![]() , а
, а ![]() . Значения i и kв десятичной системе и системе с основаниями 2 и 3 сведем в табл. 1.
. Значения i и kв десятичной системе и системе с основаниями 2 и 3 сведем в табл. 1.
Таблица 1
| 0 | 1 | 2 | 3 | 4 | 5 |
| 00 | 01 | 10 | 11 | 20 | 21 |
В соответствии с формулой (3) ОФК в этом случае записываются следующим образом:
![]()
Подставляя сюда все значения разрядов, получим систему из шести ОФК, которую представим в виде следующей матрицы значений с минимальными фазами:
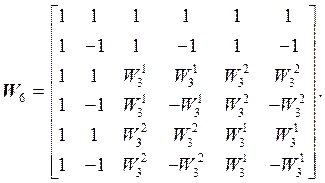 (19)
(19)
Элементы ![]() и
и ![]() имеют следующие значения:
имеют следующие значения:
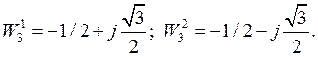
Теперь вычислим ОФК с помощью функций Радемахера. В соответствии с выражением (18) они будут равны:
![]()
![]()
После этого, пользуясь формулой (18), выразим все ОФК через эти функции:
![]()
![]()
![]()
![]()
![]()
![]()
Вычисление по этим формулам приводит к той же матрице значений ОФК (19).
_______________ . _______________
Возможен еще один способ вычисления приведенных ОФК. Он следует из матричной интерпретации выражения (3) в виде кронекеровского произведения соответствующих матриц ДЭФ:
![]() , (20)
, (20)
где
![]() (21)
(21)
Поскольку такая система ОФК может быть выражена с помощью кронекеровского произведения, то ее можно назвать системой ОФК-Кронекера. В частном случае, при ![]() она переходит в систему ВКФ-Адамара [2].
она переходит в систему ВКФ-Адамара [2].
Пример 2. Вычислить матрицу ОФК кронекеровским способом для условия предыдущего примера.
Решение. В этом случае
![]()
где
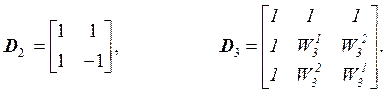
Поэтому
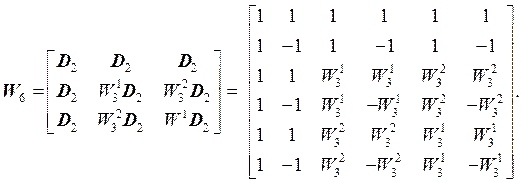 (22)
(22)
Матрицы (19) и (22) совпадают.
_______________ . _______________
Кронекеровская система является только одной из возможных полных базисных систем, использующих ОФК. На основе функций 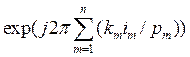 можно построить целое семейство базисов с симметрическими и унитарными матрицами, число которых зависит от конкретной величины N. Причем возможностей для организации базисных систем здесь больше, чем в ВКФ.
можно построить целое семейство базисов с симметрическими и унитарными матрицами, число которых зависит от конкретной величины N. Причем возможностей для организации базисных систем здесь больше, чем в ВКФ.
Можно отметить, кроме рассмотренных, по меньшей мере еще два способа построения таких базисов. Первый способ основывается на использовании формул (2), (18) или (20) для всех возможных комбинаций сомножителей в произведении ![]() для N. Если все сомножители
для N. Если все сомножители ![]() разные, то он позволяет получить n! различных базисных систем ОФК-Кронекера.
разные, то он позволяет получить n! различных базисных систем ОФК-Кронекера.
Пример 3. Построить все системы ОФК-Кронекера для N=6.
Решение. В этом случае возможны два варианта разложения N=6 на множители: ![]() и
и ![]() . Для первого варианта система ОФК-Кронекера получена и приведена в предыдущих примерах. Для второго варианта имеем
. Для первого варианта система ОФК-Кронекера получена и приведена в предыдущих примерах. Для второго варианта имеем
![]() .
.
Поэтому
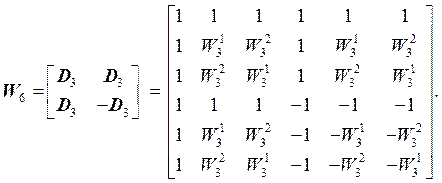 (23)
(23)
Полученная матрица (23) отличается от матрицы (22).
_______________ . _______________
Второй способ формирования базисных ОФК-систем состоит в перестановке строк и столбцов любой матрицы ОФК-Кронекера, полученной первым способом, по закону определенной замкнутой операции над индексами k и i ОФК (напомним, что замкнутой считается такая операция над индексом, результат которой, изменяя порядок следования значений индекса, не меняет самого диапазона его изменения, т.е. результирующий индекс пробегает те же значения, что и исходный, но в другой последовательности). Такими операциями являются, например, инверсия кода индекса и кодирование Грея индекса, обобщенные на случай многоосновной системы счисления. Рассмотрим эти операции.
Если число kв многоосновной системе счисления представляется выражением (1), то инверсное ему число ![]() в этой же системе счисления записывается следующим образом:
в этой же системе счисления записывается следующим образом:
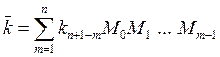 (24)
(24)
где
![]()
Обобщенная инверсия, как и двоичная, и p-ичная инверсии, сводится к записи разрядов кода числа k в обратном порядке. Однако веса разрядов в многоосновной системе, где диапазоны изменения разрядов ![]() в общем случае не совпадают, должны быть изменены по закону (24). При
в общем случае не совпадают, должны быть изменены по закону (24). При ![]() обобщенная инверсия переходит в p-ичную инверсию и инверсное число
обобщенная инверсия переходит в p-ичную инверсию и инверсное число ![]() имеет более привычный вид записи:
имеет более привычный вид записи:
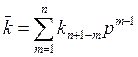 .
.
Пример 4. Найти инверсные значения целочисленного индекса, принадлежащего диапазону [0,6).
Решение. В этом случае 6=2· 3, поэтому ![]() а
а ![]() . В системе счисления с основаниями 2 и 3 числа k и
. В системе счисления с основаниями 2 и 3 числа k и ![]() будут иметь следующий вид:
будут иметь следующий вид: ![]() ,
, ![]() . Их значения в различных формах записи приведены в табл. 2.
. Их значения в различных формах записи приведены в табл. 2.
Таблица 2
k | 0 | 1 | 2 | 3 | 4 | 5 |
| 00 | 01 | 10 | 11 | 20 | 21 |
| 00 | 10 | 01 | 11 | 02 | 12 |
| 0 | 3 | 1 | 4 | 2 | 5 |
| 00 | 01 | 11 | 10 | 20 | 21 |
| 0 | 1 | 3 | 2 | 4 | 5 |
_______________ . _______________
Код Грея ![]() числа k в многоосновной системе счисления вычисляется по следующему алгоритму:
числа k в многоосновной системе счисления вычисляется по следующему алгоритму: ![]() , который отличается от соответствующего алгоритма в системе счисления с одним основанием только использованием различных модулей при формировании разрядов кода.
, который отличается от соответствующего алгоритма в системе счисления с одним основанием только использованием различных модулей при формировании разрядов кода.
Пример 5. Найти значения кода Грея для индекса k предыдущего примера.
Решение. Так как в этом случае ![]() , то
, то ![]() а
а
![]() . Результаты расчетов по этим формулам приведены в табл. 2.
. Результаты расчетов по этим формулам приведены в табл. 2.
______________ . _______________
Рассмотренные операции позволяют получить новые полные ортонормированные мультипликативные системы ОФК. Для этого необходимо в матрице любой известной системы ОФК осуществить сначала перестановку строк, а затем – столбцов (можно и наоборот) по закону этих операций. В результате будут получены новые симметрические и унитарные матрицы ОФК. Перестановка только строк или только столбцов исходной матрицы приводит к несимметрическим результирующим матрицам.
Продемонстрируем процесс формирования симметрических матриц на конкретных примерах.
Пример 6. Построить матрицу ОФК из матрицы ОФК-Кронекера (19) с использованием операции обобщенной инверсии индексов.
Решение. В соответствии с данными табл. 2 произведем следующее переупорядочение матрицы (19): первую строку перемещаем на место второй, а вторую – на место четвертой, третью – на место первой, четвертую – на место третьей, а нулевую и пятую строки оставляем на своих местах. В результате получается следующая промежуточная матрица:
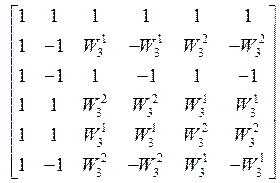
Эта матрица несимметрическая. Для получения из нее симметрической матрицы необходимо выполнить аналогичные перестановки её столбцов. Тогда будет получена следующая итоговая матрица:
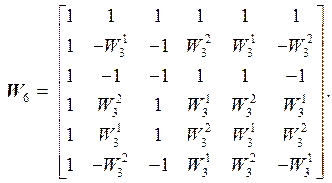 (25)
(25)
Эта матрица ОФК является симметрической и отличается от исходной.
_______________ . _______________
Пример 7. Построить матрицу ОФК из той же матрицы ОФК-Кронекера (19) с использованием кодирования Грея.
Решение. В соответствии с данными табл. 2 в этом случае процедура перестановок существенно проще: нулевые, первые, четвертые и пятые строки и столбцы остаются на месте, а вторые и третьи меняются местами. В итоге получается следующая матрица ОФК:
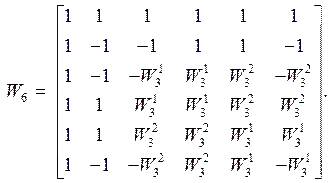 (26)
(26)
Эта матрица так же симметрическая и по структуре не совпадает ни с матрицей (19), ни с матрицей (25).
_______________ . _______________
Результаты приведенных примеров показывают, что все матрицы, полученные различными способами, отличаются друг от друга по структуре, хотя и обладают одинаковыми общими свойствами. Это говорит о том, что рассмотренные способы не подменяют друг друга и являются инструментом для построения новых полных ортонормированных и мультипликативных базисных систем.
Перейдем теперь к синтезу алгоритмов быстрого преобразования в базисе обобщенных функций Крестенсона (БПК). Вариантов построения БПК существует еще больше, чем быстрых преобразований в базисе ВКФ, поскольку возможно образование значительно большего числа систем ОФК. В качестве примера приведем методы синтеза БПК только для ОФК-систем Кронекера.
Остановимся сначала на случае представления числа отсчетов сигнала в виде произведения двух сомножителей: ![]() , где
, где ![]() и
и ![]() являются целыми положительными числами. Преобразуем одномерный массив
являются целыми положительными числами. Преобразуем одномерный массив ![]() в двумерную таблицу
в двумерную таблицу ![]() с помощью подстановки
с помощью подстановки ![]() . Эта подстановка соответствует представлению величины
. Эта подстановка соответствует представлению величины ![]() в позиционной системе счисления с основаниями
в позиционной системе счисления с основаниями ![]() и
и ![]() при числе разрядов
при числе разрядов ![]() . Тогда прямые ДПФ в базисе ОФК (14) без нормирующего множителя
. Тогда прямые ДПФ в базисе ОФК (14) без нормирующего множителя ![]() можно записать так:
можно записать так:
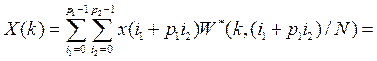
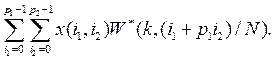
Рассмотрим спектральные составляющие с номерами, изменяющимися по такому же закону, что и номера отсчетов, т.е. с ![]()
![]()
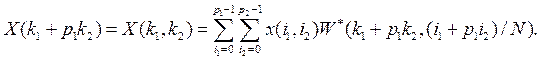 (27)
(27)
Используя свойства позиционных кодов в системе с переменным основанием, можно записать, что
![]()
![]() (28)
(28)
где ![]() является, как и ранее в выражении (8), обозначением операции поразрядного суммирования по переменному модулю. Тогда в соответствии со свойствами мультипликативности и двойственности ОФК выражение (27) можно преобразовать к виду
является, как и ранее в выражении (8), обозначением операции поразрядного суммирования по переменному модулю. Тогда в соответствии со свойствами мультипликативности и двойственности ОФК выражение (27) можно преобразовать к виду
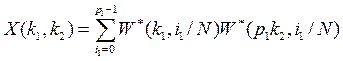
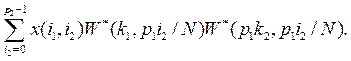
Дальнейшее упрощение этого выражения зависит от значений приведенных в нем ОФК. Чтобы их получить, воспользуемся записью ОФК в виде формулы (2). Тогда имеем
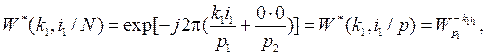
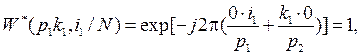
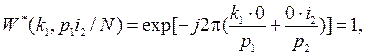
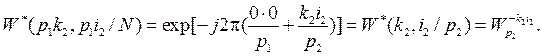
Учитывая эти соотношения, получим следующую запись общего спектра сигнала:
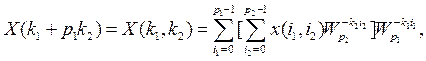
![]() (29)
(29)
Полученное выражение представляет собой алгоритм БПК для случая разложения Nна два множителя.
Его можно записать в более удобной для вычислений форме, если обозначить внутреннюю сумму в выражении (29) в виде двумерной величины
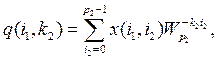
![]() . (30)
. (30)
Тогда полный спектр будет равен
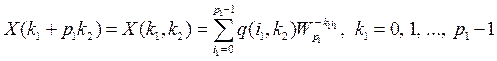 . (31)
. (31)
Последовательность действий в таком алгоритме такова: сначала одномерный сигнал преобразуется в двумерную таблицу ![]() размерностью
размерностью ![]() , после чего с помощью
, после чего с помощью ![]() -точечных ДПФ по каждой из её строк вычисляется таблица промежуточных данных
-точечных ДПФ по каждой из её строк вычисляется таблица промежуточных данных ![]() , из которой затем путем выполнения
, из которой затем путем выполнения ![]() -точечных ДПФ по всем её столбцам формируется таблица искомых спектральных коэффициентов
-точечных ДПФ по всем её столбцам формируется таблица искомых спектральных коэффициентов ![]() . Переход от одномерных массивов к двумерным таблицам и обратно осуществляется по правилам взаимосвязи одномерных и многомерных индексов. Поскольку в этом алгоритме БПК отсчеты сигнала и спектра по строкам соответствующих таблиц располагаются с прореживанием, то он является алгоритмом с прореженным порядком следования отсчетов сигнала и спектра (алгоритмом первого типа).
. Переход от одномерных массивов к двумерным таблицам и обратно осуществляется по правилам взаимосвязи одномерных и многомерных индексов. Поскольку в этом алгоритме БПК отсчеты сигнала и спектра по строкам соответствующих таблиц располагаются с прореживанием, то он является алгоритмом с прореженным порядком следования отсчетов сигнала и спектра (алгоритмом первого типа).
Для БПК (29) число комплексных сложений ![]() и умножений
и умножений ![]() равно:
равно:
![]() , (32)
, (32)
![]() . (33)
. (33)
В последней оценке числа умножений учтено, что умножения на единичные значения элементов матрицы ДЭФ, расположенные в её нулевой строке и нулевом столбце, являются тривиальными. Исключение из алгоритма умножений на другие тривиальные значения ДЭФ приводит к оптимизированным вариантам БПК. Для них оценка числа умножений еще более уменьшается.
Пример 8. Записать алгоритм БПК-Кронекера для ![]() .
.
Решение. Пусть ![]() и
и ![]() . Тогда массив сигнала
. Тогда массив сигнала ![]() превращается в таблицу
превращается в таблицу ![]()
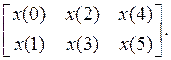
Алгоритм вычисления двумерного спектра ![]() в соответствии с общим алгоритмом (29) будет выглядеть так:
в соответствии с общим алгоритмом (29) будет выглядеть так:
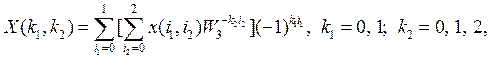
где учтено, что ![]() Промежуточные величины
Промежуточные величины
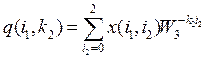
и алгоритм БПК:

Дальнейшую последовательность действий можно представить в виде следующих двух этапов.
Этап 1. Расчет промежуточных величин:
![]()
![]()
![]()
![]()
Принимая ![]() получим
получим
![]()
![]() ,
,
![]()
![]()
![]()
![]()
Таблица этих промежуточных величин будет иметь следующий вид:
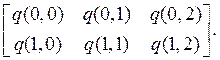
Этап 2. Расчет искомого спектра:
![]()
![]()
поэтому при ![]()
![]()
![]()
![]()
Этим значениям соответствуют итоговые таблицы
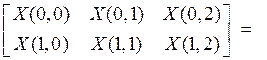
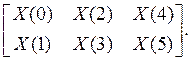
В алгоритме выполняются 18 сложений и 8 умножений. Расчет по формулам (32), (33) дает 18 сложений и 11 умножений. Меньшее число реальных умножений связано с тем, что используемое в данном примере 2-точечное ДПФ выполняется без умножений. Сигнальный граф этого алгоритма приведен на рис. 1а.
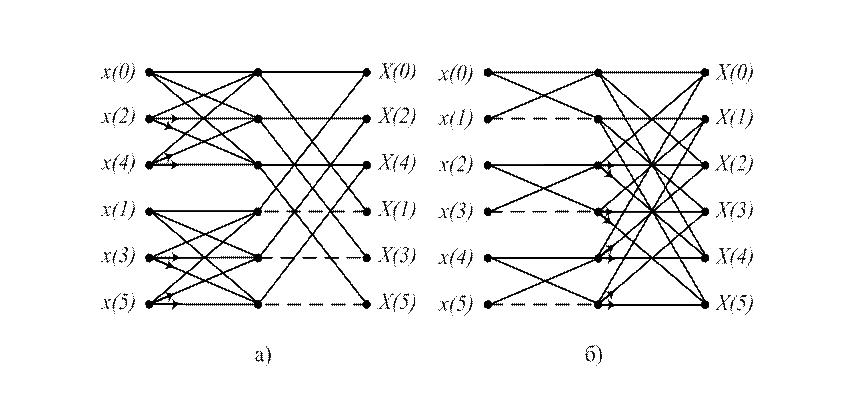
Рис. 1. Сигнальный граф полного БПК-Кронекера первого (а) и второго (б) типа для N=9
____________ . _______________
Если в свою очередь один из сомножителей ![]() или
или ![]() также раскладывается на два множителя, то приведенный алгоритм рекурсивно можно применить и для быстрого вычисления
также раскладывается на два множителя, то приведенный алгоритм рекурсивно можно применить и для быстрого вычисления ![]() -точечных или
-точечных или ![]() -точечных ДПФ. Это повлечет за собой дополнительное прореживание сигнала и спектра и, в конечном итоге, к дополнительному сокращению объема вычислений. В общем случае при
-точечных ДПФ. Это повлечет за собой дополнительное прореживание сигнала и спектра и, в конечном итоге, к дополнительному сокращению объема вычислений. В общем случае при
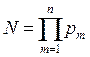 ,
,
одномерные массивы ![]() и
и ![]() с помощью подстановок
с помощью подстановок
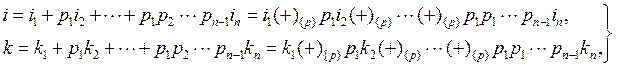 (34)
(34)
где ![]() , преобразуются в многомерные таблицы
, преобразуются в многомерные таблицы ![]() и
и ![]() , связь между которыми устанавливает следующее аналитическое выражение:
, связь между которыми устанавливает следующее аналитическое выражение:
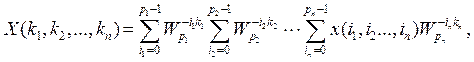
![]() (35)
(35)
Это и есть полный алгоритм БПК-Кронекера с прореженным порядком следования отсчетов сигнала и спектра, содержащий ![]() уровней прореживания.
уровней прореживания.
Реализация полного алгоритма БПК потребует выполнения
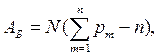
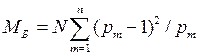 (36)
(36)
сложений и умножений. Некоторые из этих умножений могут оказаться тривиальными. Их исключение из алгоритма позволяет еще больше оптимизировать его.
В алгоритмах БПК-Кронекера (29) и (35) можно поменять последовательность суммирования и порядок следования индексов, в результате чего будут получены другие модификации БПК, обладающие такими же реализационными характеристиками. В частности, если порядок следования индексов и сумм изменить на обратный, что приведет к обработке транспонированных таблиц сигнала и спектра, то можно получить второй тип алгоритма БПК-Кронекера с естественным порядком следования отсчетов сигнала и спектра. Для ![]() такой алгоритм имеет следующий вид:
такой алгоритм имеет следующий вид:
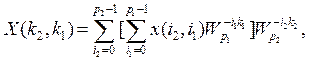
![]() , (37)
, (37)
а для ![]() он представляется следующим образом:
он представляется следующим образом:
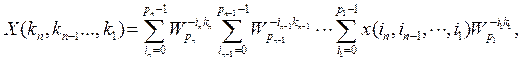
(38)
![]()
Пример 9. Записать алгоритм БПК-Кронекера второго типа для N=6.
Решение.Примем![]() .Таблица сигнала
.Таблица сигнала![]()
![]()
![]() имеет следующий вид
имеет следующий вид
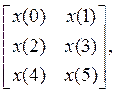
а алгоритм БПК выглядит так:
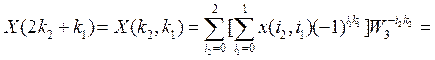
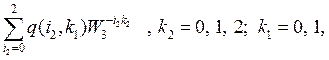
где
![]()
Этап 1. Расчет промежуточных величин ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Они образуют таблицу
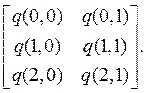
Этап 2 . Расчет спектра ![]()
![]()
![]()
![]()
Результирующие таблицы имеют вид:
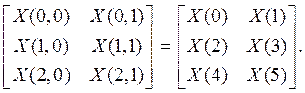
Сигнальный граф этого алгоритма приведен на рис. 1б. По сложности он совпадает с алгоритмом первого типа.
_______________ . _______________
В выражении для Nпорядок сомножителей можно изменить. Это приводит к БПК для других систем ОФК, отличных от систем Кронекера.
Таким образом, полученные результаты, включая методы формирования различных базисных систем на основе обобщенных функций Крестенсона в системах счисления с переменными основаниями, их свойства и быстрые алгоритмы вычисления спектра, составляют теоретическую основу для решения проблемы выбора оптимального базиса для широкого круга задач обработки сигналов (фильтрации, распознавания, сжатия, кодирования и т.п.) в условиях действия жестких ограничений на вычислительную сложность алгоритмов обработки. Особенно перспективным может оказаться применение этих базисов для исследования ![]() -линейных систем и
-линейных систем и ![]() -стационарных случайных процессов, использующих обобщенный временной сдвиг в виде поразрядного модулярного сложения с различными модулями.
-стационарных случайных процессов, использующих обобщенный временной сдвиг в виде поразрядного модулярного сложения с различными модулями.
СПИСОК ЛИТЕРАТУРЫ
- Залманзон Л.А. Преобразования Фурье, Уолша, Хаара и их применение в управлении, связи и других областях. – М.: Наука, 1989. – 496 с.
- Трахтман А.М., Трахтман В.А. Основы теории дискретных сигналов на конечных интервалах. – М.: Сов. радио, 1975.- 208 с.
- Власенко В.А., Лаппа Ю.М., Ярославский Л.П. Методы синтеза быстрых алгоритмов свертки и спектрального анализа сигналов. - М.: Наука, 1990. – 180 с.
Публикации с ключевыми словами: сигнал, спектр, базис Крестенсона, многоосновная система счисления, быстрые преобразования Фурье
Публикации со словами: сигнал, спектр, базис Крестенсона, многоосновная система счисления, быстрые преобразования Фурье
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



