научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
DOI: 10.7463/0412.0355729
УДК 519.6
МГТУ им. Н.Э. Баумана
Введение
Алгоритмы решения задач глобальной безусловной оптимизации можно разделить на три группы – детерминированные, стохастические и эвристические. Эвристические алгоритмы, в свою очередь, разделяют на эволюционные и поведенческие алгоритмы. Алгоритм роя частиц (ParticleSwarmOptimization, PSO), рассматриваемый в данной работе, является поведенческим алгоритмом безусловной оптимизации [1]. Эффективность алгоритма PSOв значительной мере зависит от используемой алгоритмом топологии соседства частиц. Так, например, топология типа клика обеспечивает высокую эффективность алгоритма, но может привести к его преждевременной сходимости к некоторому локальному минимуму целевой функции. В случае топологии типа кольцо преждевременной сходимости можно избежать, но алгоритм оказывается эффективным лишь для сложных многоэкстремальных функций.
Целью данной работы является исследование эффективности ко-алгоритмической гибридизации алгоритмов PSOс различными топологиями соседства частиц [2]. Точнее говоря, рассматривается двухпопуляционный ко-алгоритм CPSOна основе алгоритмов PSO, использующих топологии соседства типа клика и кольцо.
1. Алгоритм роя частиц
Алгоритм PSO был опубликован в 1995 году. В основу алгоритма положена социально-психологическая поведенческая модель толпы. Агентами в алгоритме являются частицы в пространстве параметров задачи оптимизации, обладающие в этом пространстве положениями и скоростями. На каждой итерации при определении следующего положения частицы учитывается информация о наилучшей частице из числа соседних частиц, а также информация о положении данной частицы на той итерации, когда этой частице соответствовало наилучшее значение функции цели. Известно большое число модификаций алгоритма, большинство из которых являются последовательными, хотя известны и параллельные варианты алгоритма [1].
Рассматриваем задачу глобальной безусловной минимизации целевой функции ![]() в
в ![]() -мерном арифметическом пространстве
-мерном арифметическом пространстве ![]() :
:

Множество частиц обозначим ![]() , где
, где ![]() – число частиц в рое (размер популяции). В момент времени tкоординаты частицы
– число частиц в рое (размер популяции). В момент времени tкоординаты частицы ![]() определяются
определяются ![]() -мерными векторами ее координат
-мерными векторами ее координат ![]() и скорости
и скорости ![]() . Начальные координаты и скорости частицы
. Начальные координаты и скорости частицы ![]() равны
равны ![]() ,
, ![]() соответственно. Итерации метода PSO выполняются в соответствии с формулами
соответственно. Итерации метода PSO выполняются в соответствии с формулами
![]()
![]()
Здесь ![]() -
- ![]() -мерный вектор псевдослучайных чисел, равномерно распределенных в интервале
-мерный вектор псевдослучайных чисел, равномерно распределенных в интервале ![]() ;
; ![]() - символ покомпонентного умножения векторов;
- символ покомпонентного умножения векторов; ![]() - вектор координат частицы
- вектор координат частицы ![]() с наилучшим (в смысле формулы (1)) значением целевой функции
с наилучшим (в смысле формулы (1)) значением целевой функции ![]() за все время поиска
за все время поиска ![]() ;
; ![]() - вектор координат соседней с данной частицы с наилучшим за то же время значением целевой функции;
- вектор координат соседней с данной частицы с наилучшим за то же время значением целевой функции; ![]() ,
, ![]() ,
, ![]() - свободные параметры алгоритма. Параметр
- свободные параметры алгоритма. Параметр ![]() определяет «инерционные» свойства частицы,
определяет «инерционные» свойства частицы, ![]() – ее «когнитивные» свойства,
– ее «когнитивные» свойства, ![]() – «социальность» частицы [1]. Рекомендуемые значения параметров
– «социальность» частицы [1]. Рекомендуемые значения параметров ![]() ,
, ![]() ,
, ![]() равны, соответственно, 0,7298; 1,49618; 1,49618.
равны, соответственно, 0,7298; 1,49618; 1,49618.
Соседство частиц в рое определяется топологией соседства, которую задают неориентированным графом. Вершины графа соответствуют частицам роя, а ребра связывают непосредственных соседей. В алгоритме PSO обычно используют следующие топологии соседства частиц:
· топология клика (глобальная оптимальная топология);
· топология кольцо (локальная оптимальная топология);
· топология двумерный тор (топология фон Неймана);
· топология кластер.
Две первые топологии, которые используются в алгоритме CPSO, иллюстрируют рисунки 1, 2. Топологии клика соответствует полносвязный граф (рисунок 1), в котором соседями каждой из частиц ![]() являются остальные
являются остальные ![]() частицы. Диаметр клики равен единице. В топологии кольцо (рисунок 2) соседями каждой из частиц являются всего две частицы, которые имеют соседние номера. Диаметр соответствующего графа равен
частицы. Диаметр клики равен единице. В топологии кольцо (рисунок 2) соседями каждой из частиц являются всего две частицы, которые имеют соседние номера. Диаметр соответствующего графа равен  .
.

Рис. 1. Топология соседства типа клика: ![]()
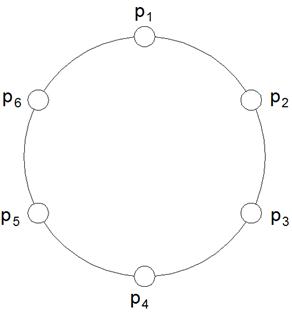
Рис. 2. Топология соседства частиц кольцо: ![]()
Диаметр графа, соответствующего используемой роем топологии соседства частиц, определяет скорость распространения информации в рое. В рое с топологией соседства клика лучшее значение целевой функции, достигнутое той или иной частицей, сразу становится известным всем остальным частицам роя. Самую низкую скорость распространения информации обеспечивает топология кольцо.
Известно, что топология клика обеспечивает высокую скорость сходимости алгоритма PSO, но может привести к его преждевременной сходимости к некоторому локальному минимуму целевой функции. Так что данную топологию целесообразно использовать при оптимизации одноэкстремальных функций. Топология кольцо эффективна при оптимизации сложных многоэкстремальных функций. Причина этого заключается в том, что частицы роя, расположенные далеко друг от друга в кольце, слабо связаны друг с другом и могут эффективно исследовать различные части области поиска. Топология обеспечивает слабое «притяжение» частиц к локальным минимумам целевой функции, что позволяет избежать преждевременной сходимости.
2. Ко-алгоритмическая гибридизация алгоритмов роя частиц
В основе ко-алгоритмической гибридизации популяционных алгоритмов оптимизации лежит следующая основная идея. Одновременно в пространстве поиска эволюционируют несколько субпопуляций, каждая из которых базируется на одном из популяционных алгоритмов и решает задачу оптимизации (1). Каждая из субпопуляций «борется» за вычислительные ресурсы, которые по окончании заданного числа итераций перераспределяют в пользу более эффективной из субпопуляций.
Вообще говоря, ко-алгоритм может быть построен на основе различных поисковых алгоритмов оптимизации. Классический ко-алгоритм предполагает использование в качестве субпопуляционных алгоритмов генетического алгоритма и называется, поэтому, генетическим коэволюционным алгоритмом. В этом алгоритме одинаковыми для всех субпопуляционных алгоритмов являются структура и значения свободных параметров, за исключением параметров, определяющих генетические операторы селекции и формирования нового поколения [2].
В данной работе в качестве субпопуляционных алгоритмов используются алгоритмы PSO, которые по сравнению с генетическим алгоритмом обладает рядом преимуществ [3, 4]:
- алгоритм PSOобладает «памятью», поскольку знание о лучшем из найденных решений рано или поздно становится известным всем частицам популяции (в генетическом алгоритме лучшее решение может быть уничтожено при изменении популяции);
‑ алгоритм PSOподразумевает «сотрудничество» между частицами, так как частицы в рое делятся информацией между собой.
С другой стороны, в алгоритм PSO, также как и в генетическом алгоритме, возможна преждевременная сходимость.
Для генетического коэволюционного алгоритма рекомендуется использовать общее число субпопуляций ![]() , равное три - пять. В данной работе используем субпопуляции
, равное три - пять. В данной работе используем субпопуляции
![]() ,
, ![]()
так что ![]() .
.
Кроме числа субпопуляций, наиболее важными свободными параметрами ко-алгоритма являются:
‑ величина ресурса ![]() – максимально допустимое число испытаний (вычислений значений целевой функции);
– максимально допустимое число испытаний (вычислений значений целевой функции);
‑ интервал адаптации ![]() , где T – максимально допустимое число итераций;
, где T – максимально допустимое число итераций;
- величина штрафа ![]() ;
;
‑ минимально допустимый размер субпопуляции ![]() .
.
На этапе инициализации ко-алгоритма величина ресурса ![]() распределяется поровну между субпопуляциями. Условием окончания итераций ко-алгоритма может быть исчерпание этого ресурса.
распределяется поровну между субпопуляциями. Условием окончания итераций ко-алгоритма может быть исчерпание этого ресурса.
Интервал адаптации ![]() – это число итераций, в течение которых субпопуляции не обмениваются информацией друг с другом, но итерируют обособленно. Чем меньше значение
– это число итераций, в течение которых субпопуляции не обмениваются информацией друг с другом, но итерируют обособленно. Чем меньше значение ![]() , тем меньше возможностей у субпопуляционных алгоритмов продемонстрировать особенности своего поведения. Все субпопуляции показывают в этом случае близкие результаты, и эффект гибридизации исчезает. При больших значениях величины
, тем меньше возможностей у субпопуляционных алгоритмов продемонстрировать особенности своего поведения. Все субпопуляции показывают в этом случае близкие результаты, и эффект гибридизации исчезает. При больших значениях величины ![]() эффективность ко-алгоритма также может быть низкой, поскольку в этом случае значительное число субпопуляций может оказаться в неперспективных подобластях пространства поиска.
эффективность ко-алгоритма также может быть низкой, поскольку в этом случае значительное число субпопуляций может оказаться в неперспективных подобластях пространства поиска.
Штраф назначается проигравшей субпопуляции (проигравшему субпопуляционному алгоритму). Величина штрафа ![]() имеет смысл доли, на которую сокращается размер проигравшей субпопуляции. Значение штрафа не следует назначать слишком маленьким, так как в таком случае субпопуляционные алгоритмы могут не ощутить на себе влияния штрафа. Также значение
имеет смысл доли, на которую сокращается размер проигравшей субпопуляции. Значение штрафа не следует назначать слишком маленьким, так как в таком случае субпопуляционные алгоритмы могут не ощутить на себе влияния штрафа. Также значение ![]() не стоит выбирать слишком близким к единице, поскольку в этом случае проигравшие субпопуляционные алгоритмы окажутся неэффективными в силу малых мощностей своих популяций.
не стоит выбирать слишком близким к единице, поскольку в этом случае проигравшие субпопуляционные алгоритмы окажутся неэффективными в силу малых мощностей своих популяций.
Минимально допустимый размер субпопуляции ![]() ограничивает снизу размер проигравших популяций. Значение этого параметра назначают, исходя из отмеченной выше неэффективности малых субпопуляций. Обычно используют не абсолютные значения величины
ограничивает снизу размер проигравших популяций. Значение этого параметра назначают, исходя из отмеченной выше неэффективности малых субпопуляций. Обычно используют не абсолютные значения величины ![]() , а ее относительные значения
, а ее относительные значения
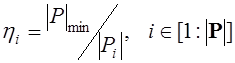 .
.
Для коэволюционного генетического алгоритма рекомендованные значения указанных свободных параметров алгоритма приведены в таблице 1 [2, 5].
Таблица 1
Рекомендованные значения свободных параметров коэволюционного генетического алгоритма
Параметр | Рекомендованное значение |
| 3 ÷ 5 |
| 5 ÷ 7 |
| 0,02 ÷ 0,15 |
| (0,05 ÷ 0,35) |
Блок-схема алгоритма CPSO имеет вид, представленный на рисунке 3.
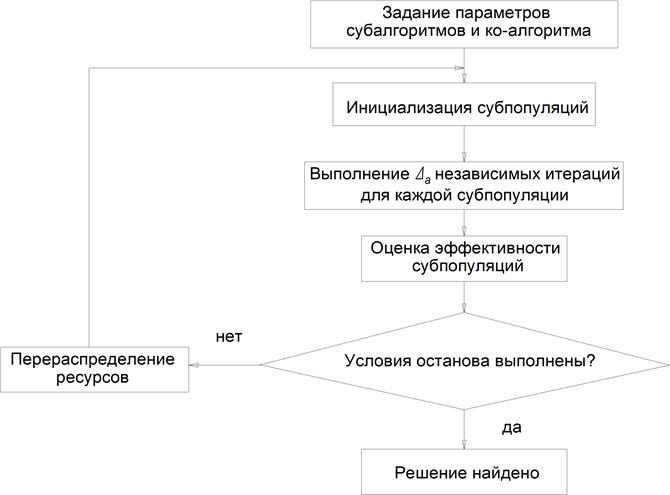
Рис. 3. Общая схема ко-алгоритма
Рассмотрим основные шаги ко-алгоритма.
1) Задание параметров субалгоритмов и ко-алгоритма.
Основные свободные параметры, значения которых должны быть определены на данном шаге, перечислены выше.
2) Инициализация субпопуляций.
Инициализация субпопуляционного алгоритма PSOзаключается в присвоение всем агентам всех субпопуляций начальных положений в пространстве поиска и начальных скоростей.
3) Выполнение каждой субпопуляцией ![]() независимых итераций.
независимых итераций.
Этот шаг включает в себя асинхронное независимое выполнение заданного числа итераций ![]() каждым из субпопуляционных алгоритмов
каждым из субпопуляционных алгоритмов ![]()
![]() .
.
4) Оценка эффективности субпопуляции.
Оценка эффективности субпопуляции ![]() производится на основе оценки текущих значений ее функции пригодности:
производится на основе оценки текущих значений ее функции пригодности: ![]() ;
; ![]() ,
, ![]() . Пригодностью субпопуляции называется мера адаптации (приспособленности) этой субпопуляции к задаче оптимизации (1). Пригодность тем выше, чем ближе лучшее решение, найденное данной субпопуляцией, к положению экстремума целевой функции.
. Пригодностью субпопуляции называется мера адаптации (приспособленности) этой субпопуляции к задаче оптимизации (1). Пригодность тем выше, чем ближе лучшее решение, найденное данной субпопуляцией, к положению экстремума целевой функции.
Значение пригодности вычисляется, например, по формуле
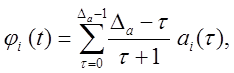
![]()
где ![]() , если субпопуляция
, если субпопуляция ![]() на итерации
на итерации ![]() включала в себя лучшего во всей популяции агента, и
включала в себя лучшего во всей популяции агента, и ![]() в противном случае. Вес величины
в противном случае. Вес величины ![]() определяется отношением
определяется отношением  , так что при
, так что при ![]() (текущая итерация) этот вес максимален и равен интервалу адаптации
(текущая итерация) этот вес максимален и равен интервалу адаптации ![]() . С уменьшение номера итерации
. С уменьшение номера итерации ![]() вес величины
вес величины ![]() в сумме (4) быстро уменьшается.
в сумме (4) быстро уменьшается.
5) Проверка выполнения условия останова.
В случае выполнения условия останова, в качестве решения принимаем наилучшее решение, найденное популяцией, и прекращаем вычисления. В противном случае переходим к следующему шагу. В качестве условия останова может быть использовано условие достижение заданного числа итераций, стагнация вычислительного процесса в течение заданного числа итераций, исчерпание ресурса ![]() .
.
6) Перераспределение ресурсов.
Перераспределение ресурсов производим на основе приспособленности субпопуляций (4). Если текущее значение пригодности субпопуляции ![]() максимально по сравнению с пригодностями остальных субпопуляций, то эта субпопуляция признается победившей, а остальные субпопуляции – проигравшими. Перераспределение ресурсов осуществляем путем сокращения размера каждой из проигравших субпопуляций на величину штрафа, определяемого величиной
максимально по сравнению с пригодностями остальных субпопуляций, то эта субпопуляция признается победившей, а остальные субпопуляции – проигравшими. Перераспределение ресурсов осуществляем путем сокращения размера каждой из проигравших субпопуляций на величину штрафа, определяемого величиной ![]() , и увеличения размера победившей субпопуляции на число, равное сумме потерь проигравших. Таким образом, общий размер популяции не изменяется.
, и увеличения размера победившей субпопуляции на число, равное сумме потерь проигравших. Таким образом, общий размер популяции не изменяется.
Если размер проигравшей субпопуляции оказывается меньше величины ![]() , то принимаем его равным этой величине. Таким образом, если
, то принимаем его равным этой величине. Таким образом, если ![]() – размер субпопуляции, проигравшей на текущем интервале адаптации, то на следующем интервале размер этой субпопуляции будет равен величине
– размер субпопуляции, проигравшей на текущем интервале адаптации, то на следующем интервале размер этой субпопуляции будет равен величине
![]()
![]() .
.
Если же субпопуляция ![]() выиграла на текущем интервале адаптации, то на следующем интервале размер этой субпопуляции будет равен
выиграла на текущем интервале адаптации, то на следующем интервале размер этой субпопуляции будет равен
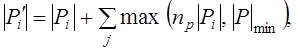
![]() ,
, ![]() .
.
3. Исследование эффективности ко-алгоритма
Исследование выполнено при варьировании значений свободных параметров алгоритма в следующих пределах:
· ![]() =5; 6; 7; 8; 9; 10;
=5; 6; 7; 8; 9; 10;
· ![]() = 0,05; 0,1; 0,15; 0,2; 0,25; 0,3;
= 0,05; 0,1; 0,15; 0,2; 0,25; 0,3;
· ![]() = 0,15; 0,2; 0,25; 0,3; 0,35; 0,4.
= 0,15; 0,2; 0,25; 0,3; 0,35; 0,4.
В качестве тестовых функций рассмотрены функции Розенброка (Rosenbrock), Химмельблау (Himmelblau) и Растригина (Rastrigin). Эффективность ко-алгоритма оцениваем средним достигнутым значением целевой функции ![]() по результатам мультистартов, а также аналогичными минимальным
по результатам мультистартов, а также аналогичными минимальным ![]() и максимальным значениями
и максимальным значениями ![]() .
.
3.1. Сравнение ко-алгоритма с базовым алгоритмом PSO
Выполнено сравнение эффективности ко-алгоритма с эффективностью базовых алгоритмов PSO с топологиями клика и кольцо. Результаты исследования представлены в таблице 2. Исследование выполнено при следующих значениях свободных параметров: число итераций T![]() равно 100; размеры популяций
равно 100; размеры популяций ![]() одинаковы и равны 16;
одинаковы и равны 16; ![]() =0,15;
=0,15; ![]() =9;
=9; ![]() . Наряду с величинами
. Наряду с величинами ![]() ,
, ![]() ,
, ![]() в таблице представлены также оценки среднеквадратичных отклонений этих величин
в таблице представлены также оценки среднеквадратичных отклонений этих величин ![]() ,
, ![]() ,
, ![]() соответственно.
соответственно.
Таблица 2
Сравнение эффективности ко-алгоритма с эффективностью базовых алгоритмов PSO
Функция | Алгоритм | |||
PSO клика | PSO кольцо | ко-алгоритм | ||
Розенброка |
| 1,1 e-004 | 2,8e-004 | 4,6e-011 |
| 3,1 e-008 | 6,7e-008 | 1,5e-020 | |
| 0,01 | 0,10 | 0,01 | |
| 2,0e-004 | 0,006 | 4,5e-004 | |
| 0,08 | 0,90 | 0.06 | |
|
| 0,01 | 1,16 | 0,02 |
Химмельблау |
| 8,2 e-007 | 3,4e-007 | 0 |
| 1,6e-012 | 3,7e-013 | 0 | |
| 5,0 e-004 | 0,05 | 0,02 | |
| 1,1 e-006 | 0,01 | 8,4e-004 | |
| 0 | 0,48 | 0,08 | |
|
| 2,1e-006 | 0,43 | 0,02 |
Растригина |
| 0,50 | 0 | 0 |
| 0,25 | 6,5 e-005 | 0 | |
| 0,64 | 1,32 | 0,32 | |
| 0,14 | 0,09 | 0,07 | |
| 1,54 | 4,14 | 0,88 | |
|
| 0,91 | 2,90 | 0,77 |
Таблица 2 показывает, что ко-алгоритм обеспечивает более точную локализацию глобального минимума рассматриваемых тестовых функций, чем базовые алгоритмы PSO.
3.2. Влияние величины интервала адаптации
Выполнено исследование эффективности ко-алгоритма в зависимости от величины интервала адаптации ![]() . Рассмотрены значения этого параметра, равные 5; 6; 7; 8; 9; 10. Исследование выполнено при следующих значениях свободных параметров ко-алгоритма, приведенных в п. 3.1. В качестве меры эффективности ко-алгоритма используем лучшее среднее по числу мультистартов значение целевой функции
. Рассмотрены значения этого параметра, равные 5; 6; 7; 8; 9; 10. Исследование выполнено при следующих значениях свободных параметров ко-алгоритма, приведенных в п. 3.1. В качестве меры эффективности ко-алгоритма используем лучшее среднее по числу мультистартов значение целевой функции ![]() .
.
Результаты исследования иллюстрирует рисунок 4. Здесь и далее ![]() ‑ популяция ко-алгоритма. Из рисунка 4а следует, что для функции Розенброка субпопуляция
‑ популяция ко-алгоритма. Из рисунка 4а следует, что для функции Розенброка субпопуляция ![]() побеждает субпопуляцию
побеждает субпопуляцию ![]() при интервале адаптации, равном, 5; 8 - 10, а субпопуляция
при интервале адаптации, равном, 5; 8 - 10, а субпопуляция ![]() побеждает субпопуляцию
побеждает субпопуляцию ![]() при
при ![]() =6, 7. Оптимальными значениями величины
=6, 7. Оптимальными значениями величины ![]() для ко-алгоритма являются значения 5; 9; 10.
для ко-алгоритма являются значения 5; 9; 10.
Для функции Химмельблау ![]() побеждает
побеждает ![]() при
при ![]() =5; 8, а
=5; 8, а ![]() побеждает
побеждает ![]() при
при ![]() =7; 9, 10 (рисунок 4б). Оптимальными для ко-алгоритма являются
=7; 9, 10 (рисунок 4б). Оптимальными для ко-алгоритма являются ![]() =5; 9; 10.
=5; 9; 10.
Аналогично для функции Растригина (рисунок 4в) первая субпопуляция побеждает вторую при ![]() =5 – 7, вторая субпопуляция первую – при
=5 – 7, вторая субпопуляция первую – при ![]() =8 – 10, и оптимальными для ко-алгоритма являются
=8 – 10, и оптимальными для ко-алгоритма являются ![]() =5; 9; 10.
=5; 9; 10.
Таким образом, исходя из результатов исследования, в качестве оптимального интервала адаптации ко-алгоритма можно рекомендовать интервал, равный девяти.
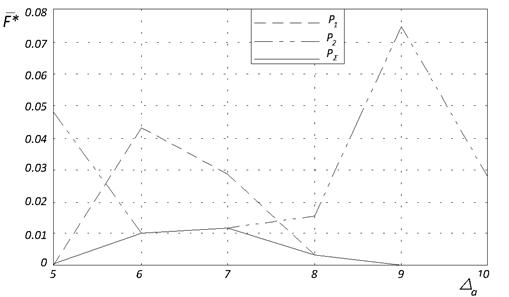
а) функция Розенброка
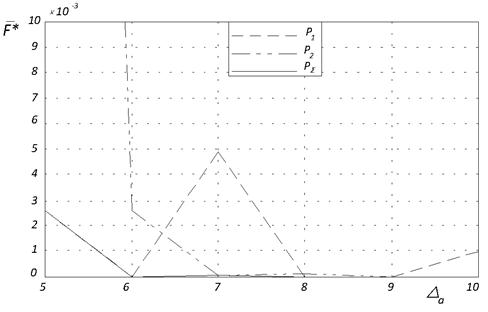
б) функция Химмельблау
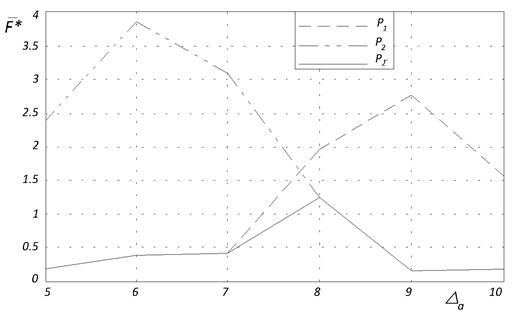
в) функция Растригина
Рис. 4. Лучшее среднее значение целевой функции ![]() в зависимости от величины интервала адаптации
в зависимости от величины интервала адаптации ![]()
3.3. Влияние коэффициента штрафа
Исследование эффективности ко-алгоритма выполнено при значениях штрафного коэффициента ![]() , равного 0,05; 0,1; 0,15; 0,2; 0,25; 0,3. Величина интервала адаптации
, равного 0,05; 0,1; 0,15; 0,2; 0,25; 0,3. Величина интервала адаптации ![]() принята равной своему оптимальному значению 9. Значения остальных свободных параметров алгоритма приведены в п. 3.1. Некоторые результаты исследования представлены на рисунке 5.
принята равной своему оптимальному значению 9. Значения остальных свободных параметров алгоритма приведены в п. 3.1. Некоторые результаты исследования представлены на рисунке 5.
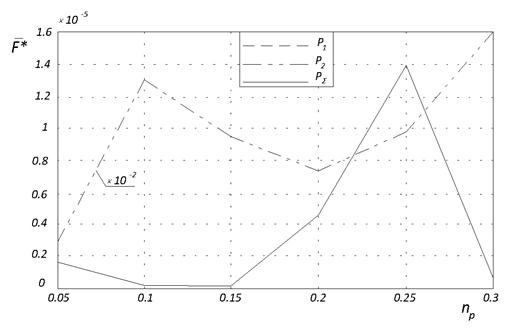
Рисунок 5а показывает, что для функции Розенброка при всех рассмотренных значений величины ![]() победителем оказывается субпопуляция
победителем оказывается субпопуляция ![]() (поэтому графики зависимостей
(поэтому графики зависимостей ![]() для субпопуляций
для субпопуляций ![]() и
и ![]() совпадают). Оптимальными являются значения штрафного коэффициента, равные 0,1 и 0,15.
совпадают). Оптимальными являются значения штрафного коэффициента, равные 0,1 и 0,15.
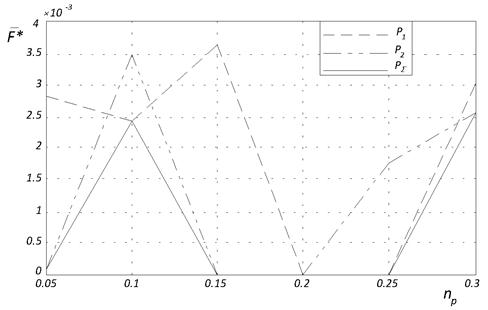
Из рисунка 5б следует, что для функции Химмельблау оптимальными являются значения коэффициента штрафа, равные 0,15 - 0,25.
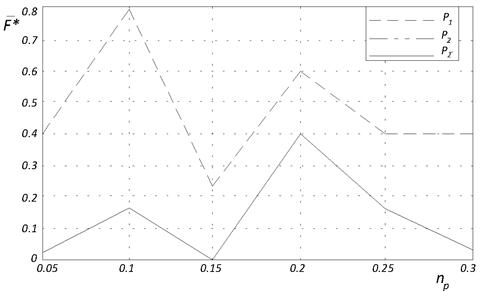
Для функции Растригина (рисунок 5в) при всех исследуемых значениях коэффициента штрафа лучших значений ![]() достигал рой с топологией кольцо (поэтому графики зависимостей
достигал рой с топологией кольцо (поэтому графики зависимостей ![]() для субпопуляций
для субпопуляций ![]() и
и ![]() совпадают). Оптимальным для функции Растригина является значение коэффициента штрафа, равное 0,15.
совпадают). Оптимальным для функции Растригина является значение коэффициента штрафа, равное 0,15.
Таким образом, в качестве оптимального значения коэффициента штрафа можно рекомендовать значение, равное 0,15.
а) функция Розенброка
б) функция Химмельблау
в) функция Растригина
Рис. 5. Лучшее среднее значение целевой функции ![]() в зависимости от значений штрафного коэффициента
в зависимости от значений штрафного коэффициента ![]()
3.4. Влияние минимального размера субпопуляций
Рассматриваем следующие величины коэффициента минимального размера субпопуляции ![]() : 0,15; 0,2; 0,25; 0,3; 0,35; 0,4. Значение коэффициента штрафа
: 0,15; 0,2; 0,25; 0,3; 0,35; 0,4. Значение коэффициента штрафа ![]() принято равным 0,15. Значения остальных свободных параметров указаны выше. Результаты исследования иллюстрирует рисунок 6.
принято равным 0,15. Значения остальных свободных параметров указаны выше. Результаты исследования иллюстрирует рисунок 6.
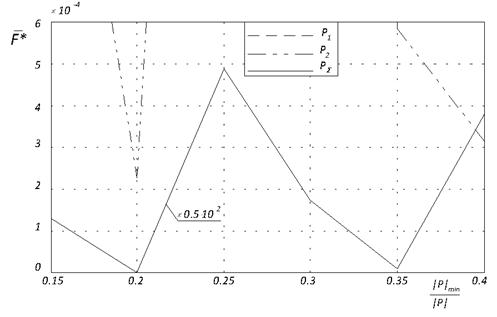
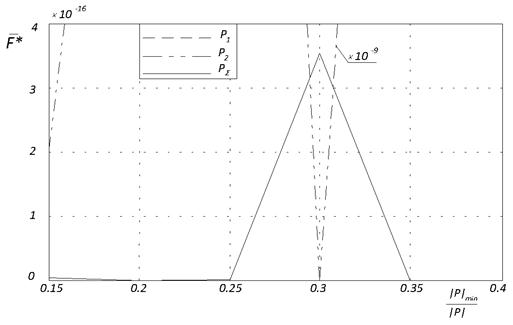
Рисунок 6а показывает, что для функции Розенброка при всех значениях параметра ![]() победителем оказалась субпопуляция
победителем оказалась субпопуляция ![]() ; оптимальные значения величины
; оптимальные значения величины ![]() равны 0,2; 0,35.
равны 0,2; 0,35.
Из рисунка 6б видно, что для функции Химмельблау победителем также оказался рой с топологией клика; оптимальные значения величины ![]() равны 0,2; 0,25; 0,35; 0,4.
равны 0,2; 0,25; 0,35; 0,4.
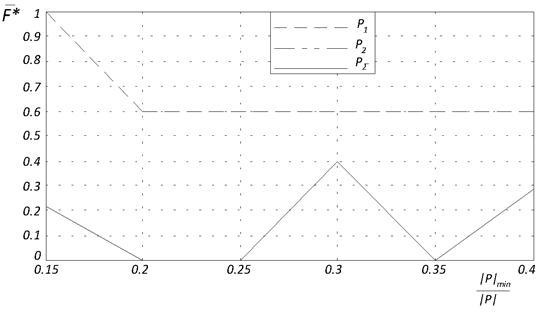
Из рисунок 6в следует, что в случае функции Растригина при всех рассмотренных значениях параметра ![]() победителем является субпопуляция
победителем является субпопуляция ![]() ; оптимальные значением
; оптимальные значением ![]() равны 0,2; 0,25; 0,35.
равны 0,2; 0,25; 0,35.
Таким образом, в качестве оптимального значения коэффициента минимального размера субпопуляции ![]() можно рекомендовать величину 0,25.
можно рекомендовать величину 0,25.
а) функция Розенброка
б) функция Химмельблау
в) функция Растригина
Рис. 6. Лучшее среднее значение целевой функции ![]() в зависимости от значений коэффициента минимального размера субпопуляции
в зависимости от значений коэффициента минимального размера субпопуляции ![]() .
.
3.5. Динамика размеров субпопуляций
Перераспределение ресурсов между субпопуляциями иллюстрирует рисунок 7. Приняты следующие значения свободных параметров алгоритма: начальные размеры субпопуляций ![]() ;
; ![]()
![]() .
.

а) Функция Розенброка
а) Функция Растригина
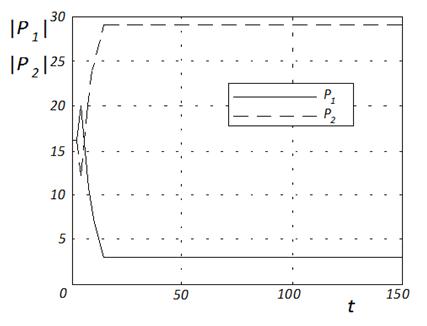
Рис. 7. Изменение размеров субпопуляций ![]() в процессе итераций
в процессе итераций
Рисунок 7а показывает, что для унимодальной функции Розенброка, как и следовало ожидать, в конечном счете, побеждает рой ![]() с топологией клика. На первых 32-х итерациях рои с переменным успехом «борются» за вычислительные ресурсы. Для многоэкстремальной функции Растригина (рисунок 7б), опять же ожидаемо, побеждает субпопуляция
с топологией клика. На первых 32-х итерациях рои с переменным успехом «борются» за вычислительные ресурсы. Для многоэкстремальной функции Растригина (рисунок 7б), опять же ожидаемо, побеждает субпопуляция ![]() с топологией кольцо. «Борьба» субпопуляций продолжается всего 14 итераций.
с топологией кольцо. «Борьба» субпопуляций продолжается всего 14 итераций.
3.6. Сходимость ко-алгоритма
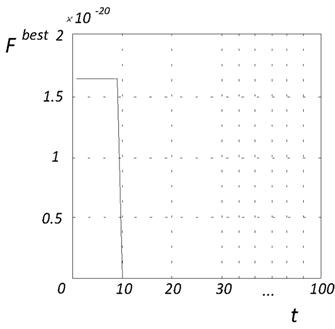
Эффективность ко-алгоритма особенно очевидна из сопоставления рисунков 8а, 8б, которые показывают характер изменения лучшего значения целевой функции ![]() в процессе итераций для ко-алгоритма и базового алгоритма PSO соответственно. Исследование выполнено при следующих значениях свободных параметров алгоритма: начальные размеры субпопуляций
в процессе итераций для ко-алгоритма и базового алгоритма PSO соответственно. Исследование выполнено при следующих значениях свободных параметров алгоритма: начальные размеры субпопуляций ![]() ;
; ![]()
![]() .
.
а) ко-алгоритм

б) базовый алгоритм PSO
Рис. 8. Сходимость ко-алгоритма и базового алгоритма PSO: функция Розенброка
Отметим высокую скорость сходимости ко-алгоритма. По сути, решение задачи получается в течение всего одного интервала адаптации (девяти итераций). Базовый алгоритм PSO обеспечивает гораздо более низкую скорость сходимости – решение достигается в течение примерно 70 итераций.
Заключение
В работе выполнено широкое исследование эффективности ко-алгоритма PSO, в котором коэволюционируют две субпопуляции с топологиями клика и кольцо. Показано, что ко-алгоритм обеспечивает более высокую эффективность по сравнению с базовыми алгоритмами PSO для всех тестируемых функций – унимодальной функции Розенброка, многоэкстремальной функции Растригина и функции Химмелблау, имеющей небольшое число экстремумов.
Для рассматриваемого набора тестовых функций найдены оптимальные значения основных свободных параметров ко-алгоритма ‑ интервал адаптации, коэффициент штрафа и коэффициент минимально допустимого размера субпопуляции. Найденные оптимальные значения свободных параметров примерно в два раза повышают скорость сходимости ко-алгоритма. По истечении всего пятидесяти итераций ко-алгоритма с этими значениями параметров достигается точность локализации глобального экстремума, примерно равная точности, достигаемой тем же алгоритмов при исходных значениях этих параметров за 200 итераций.
В развитие работы предполагается исследование эффективности ко-алгоритмической гибридизации более двух алгоритмов PSO, а также эффективности гибридизации по той же схеме различных популяционных алгоритмов, например, алгоритм роя частиц и алгоритм искусственных иммунных систем, генетический алгоритм и алгоритм роя частиц и так далее.
Литература
1. ZhouY., PeiSh. A hybrid co-evolutionary particle swarm optimization algorithm for solving constrained engineering design problems. // China Journal of computers, 2010, V. 5, N. 6, P. 965-972.
2. Shi Yu., Krohling R. A. Co-evolutionary particle swarm optimization to solve min-max problems // Evolutionary Computation, 2002, V. 2, P. 1682-1687.
3. Yongquan Zhou, Shengyu Pei. A hybrid co-evolutionary particle swarm optimization algorithm for solving constrained engineering design problems. // China: Journal of computers. June, 2010. V. 5. N. 6. P. 965-972.
4. Карпенко А.П., Селиверстов Е.Ю. Глобальная оптимизация методом роя частиц. Обзор. // Информационные технологии, 2010, № 2, С. 25-34.
5. Процыков Г.В., Семенкин Е.С., Томкин К.А. Об эффективности коэволюционного подхода в практических задачах оптимизации. // Вестник Красноярского государственного университета, 2005, №4, C. 233-239.
Публикации с ключевыми словами: алгоритм роя частиц, ко-алгоритм, гибридизация
Публикации со словами: алгоритм роя частиц, ко-алгоритм, гибридизация
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



