научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2011
УДК.62-522.2
МГТУ им. Н.Э. Баумана
Введение
Максимальная скорость движения многоосной колесной машины (МКМ), средняя скорость движения являются ее потребительским свойством и определяют конкурентоспособность образца [1]. Для МКМ эти эксплуатационные показатели определяют, кроме того, живучесть комплексов и живой силы. Повышение требований по средним скоростям движения, при всех прочих равных условиях, требует постоянного совершенствования системы первичного подрессоривания, создания подвески как сложной мехатронной системы.
Традиционная конструкция подвески колес не может разрешить противоречие, заданное в тактико-техническом задании (ТТЗ) на МКМ – обеспечение высоких средних скоростей движения на дорогах и местности и мобильности в случае преодоления крупных единичных неровностей.
Эту проблему можно решить только с помощью управляемой (регулируемой) системы подрессоривания. Однако ее эффективное применение зависит от алгоритмического и программного обеспечения, построенных на законах прикладной механики и отражающих физическую суть процессов и взаимосвязей функционирования систем колесных машин.
Необходимо подчеркнуть особенности, которыми должна обладать подвеска колес МКМ при преодолении единичных препятствий - ров, эскарп, контрэскарп и др. В этих условиях силы, действующие в подвеске и на несущую систему машин, более чем в 3 раза превышают статическую нагрузку [2]. Вся эволюция конструкций подвесок колес МКМ – это поиск компромисса между обеспечением высокой плавности хода (для чего требуется невысокие уровни демпфирования и малая жесткость подвески) и устойчивости движения на больших скоростях, с одной стороны (для чего требуется высокие уровни демпфирования и высокая жесткость подвески), и обеспечением профильной проходимости, когда с целью снижения нагрузок на несущую систему необходимо иметь длинноходную подвеску с малой жесткостью. Причем с ростом числа осей на первое место всегда выходила профильная проходимость, так как многоопорность, возникающая с ростом числа осей, существенно снижала остроту динамической нагруженности, а проблему плавности хода исключала вообще, одновременно существенно повышая остроту статической нагруженности несущей системы и вибронагруженности экипажа [3].
Одновременно с этим в настоящее время использование длинноходных подвесок МКМ сталкивается с существенными проблемами, связанными с особенностями компоновки шасси. Длинноходная подвеска занимает достаточно много места, которое требуется для размещения других агрегатов и приборов. Зачастую решение принимается в пользу подвески с коротким ходом в ущерб профильной проходимости МКМ. Однако, при этом современные подвески комплектуются сложными гидравлическими и пневматическими устройствами, имеющими широкие возможности по управлению [2]. В этой связи отмеченное выше противоречие – обеспечение профильной проходимости и высоких средних скоростей движения на дорогах и местности, может быть разрешено путем создания подвесок, в которых на первый план выходит задача создания эффективных алгоритмов управления такими системами, обеспечивающих высокую подвижность МКМ в различных условиях эксплуатации.
Одним из эффективных способов повышения параметров профильной проходимости многоосных колесных машин (МКМ) является создание управляемых систем подрессоривания. Сформулируем основные задачи, которые должна решать система автоматического управления подвеской в случае преодоления крупных единичных препятствий.
· Уменьшение углов наклона корпуса с целью обеспечения безопасности и более комфортных условий работы водителя.
· Уменьшение времени «зависания» колес, что снижает продолжительность работы несущей системы МКМ под действием повышенных нагрузок изгиба.
· Снижение пиковых значений сил в подвеске при наезде колес на препятствие, что уменьшает нагруженность несущей системы.
· Автоматизация процесса преодоления неровности, что избавляет водителя от необходимости совершать не свойственную ему работу по управлению горизонтированием корпуса, подъемом и опусканием колес различных осей.
1. Алгоритм автоматизированного преодоления эскарпа
Рассмотрим схему алгоритма преодоления эскарпа на примере движения многоосного колесного шасси с колесной формулой 8×8 полной массой 60 т при заезде на эскарп высотой 0,6 м. Максимальный ход подвесок колес составляет 0,4 м. Скорость движения МКМ 1,2 км/ч. Для описания движения колесного шасси по дорожной поверхности была использована математическая модель, разработанная на кафедре «Колесные машины» МГТУ им. Н.Э.Баумана [4]. Особенностью математической модели движения МКМ по неровностям является то, что скорость машины задается не принудительно, а формируется силами взаимодействия вращающихся колесных движителей с опорным основанием. Это позволяет получить высокую точность при моделировании реальных процессов движения МКМ. Программа разработана в среде Simulinkпрограммного комплекса Matlab.
1 этап.Наезд колес первой оси на препятствие. При этом управление подвесками колес не осуществляется (рис. 1 а).
2 этап. После наезда колес первой оси на препятствие начинается отрыв колес второй оси от дорожной поверхности, что фиксирует датчик относительных перемещений подвески (колеса «повисли» на ограничителе хода отбоя). В этот момент колеса второй оси «поджимаются», т.е. подвеска переводится в крайнее верхнее положение. Это обеспечивает гораздо более плавный заезд колес второй оси на препятствие. При этом колеса третьей и четвертой оси выдвигаются таким образом, чтобы по максимуму выровнять корпус, что обеспечивает водителю более комфортные условия (рис. 1 б, в).
3 этап. Заезд на препятствие колес третьей оси с одновременным выравниванием корпуса путем регулирования степени выдвижения колес (рис. 1 г).
4 этап. Заезд на препятствие колес четвертой оси с одновременным выравниванием корпуса путем регулирования степени выдвижения колес (рис. 1 д).
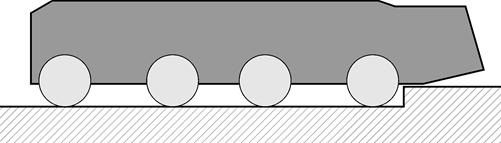
а) Начало движения
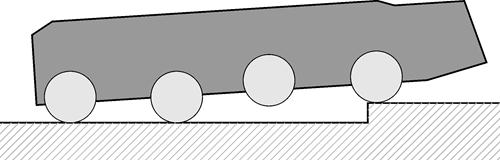
б) Установка колес второй оси в крайнее верхнее положение
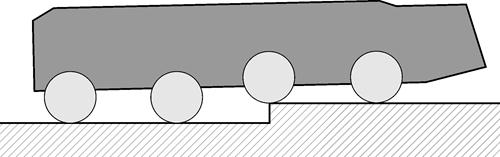
в) Выдвижение колес третьей и четвертой оси в крайнее нижнее положение, выравнивание корпуса МКМ
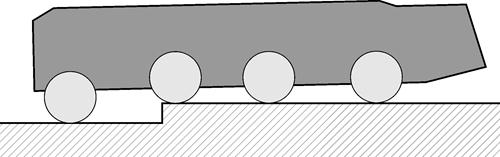
г) Заезд колес третьей оси на препятствие
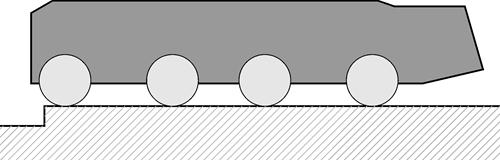
д) Заезд колес четвертой оси на препятствие
Рис. 1. Преодоление эскарпа МКМ с управляемой подвеской
Для сравнения на рис. 2 а-д приведены этапы преодоления того же препятствия шасси 8х8 с неуправляемой подвеской.
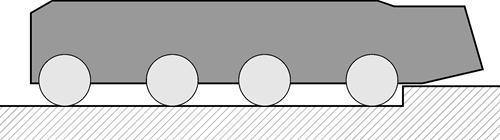
а) Начало движения
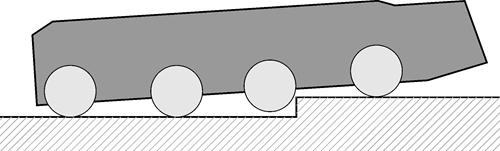
б) Вывешивание колес второй оси
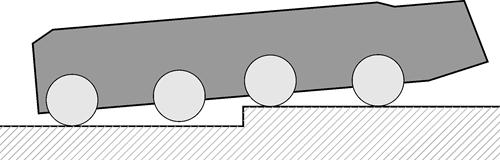
в) Вывешивание колес третьей оси
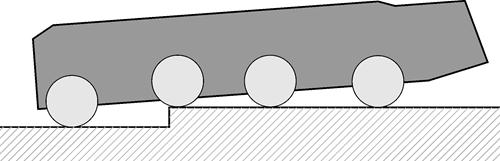
г) Заезд колес третьей оси на препятствие
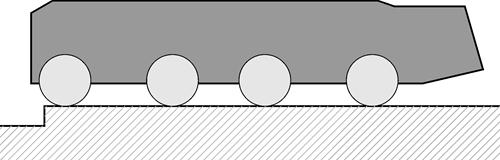
д) Заезд колес четвертой оси на препятствие
Рис. 2. Преодоление эскарпа МКМ с неуправляемой подвеской
На рис. 3 приведена блок-схема алгоритма управления подвеской МКМ, который обеспечивает реализацию рассмотренных выше этапов движения при преодолении эскарпа.
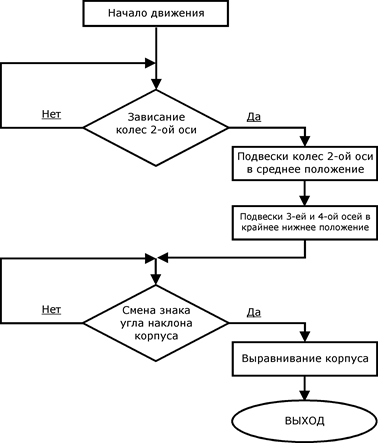
Рис. 3. Блок-схема алгоритма управления подвеской МКМ при преодолении эскарпа
2. Анализ эффективности алгоритма преодоления эскарпа
При проведении моделирования преодоления машиной траншеи были получены зависимости действующих сил в подвесках МКМ от времени для управляемой подвески (рис. 4) и для неуправляемой подвески (рис. 5). На рис. 6 и 7 приведены зависимости изменения продольного угла наклона корпуса при преодолении эскарпа для управляемой и неуправляемой подвесок соответственно.
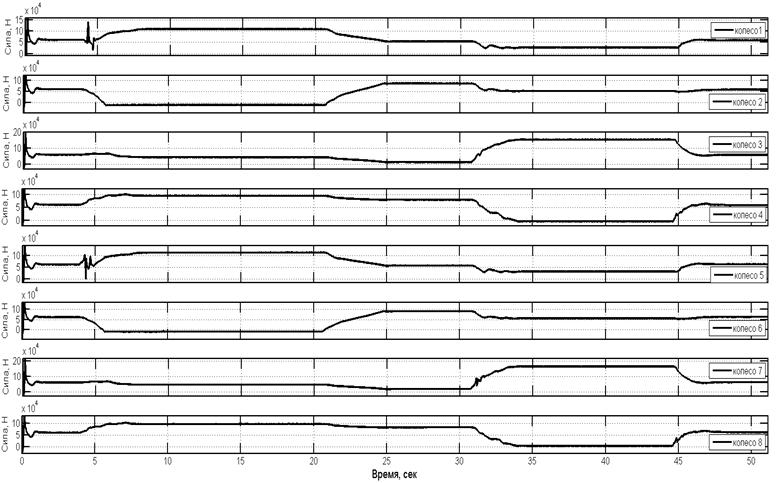
Рис. 4. Изменение сил в подвесках МКМ с управляемой подвеской при преодолении эскарпа
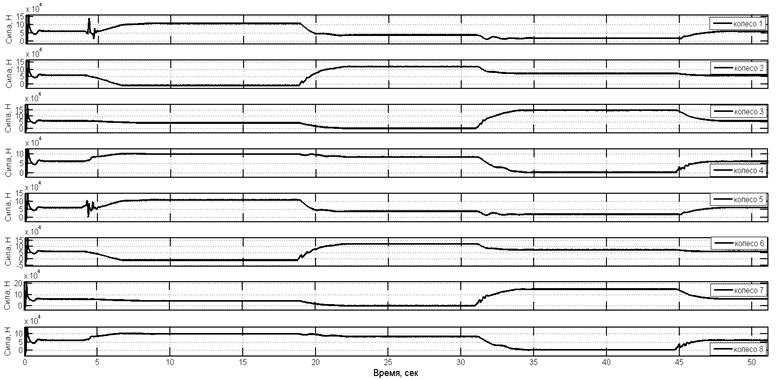
Рис. 5. Изменение сил в подвесках МКМ с неуправляемой подвеской при преодолении эскарпа
Анализ графиков на рис. 4 и 5 позволяет сделать следующие выводы.
· В случае заезда на эскарп с управляемой подвеской удалось избежать вывешивания колес третьей оси.
· Силы в подвесках колес второй оси при заезде на препятствие в случае управляемой подвески снизились на 30 % по сравнению с неуправляемой подвеской.
·
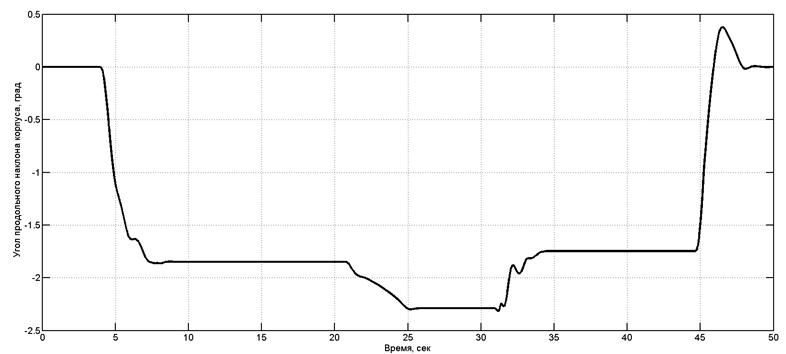
Рис. 6. Изменение угла продольного наклона корпуса МКМ с управляемой подвеской при преодолении эскарпа
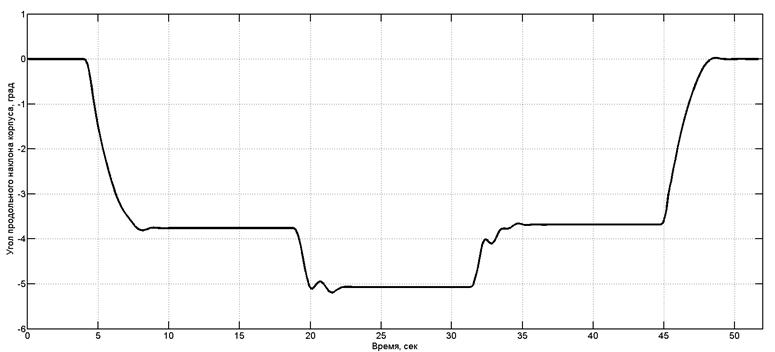
Рис. 7. Изменение угла продольного наклона корпуса МКМ с неуправляемой подвеской при преодолении эскарпа
Анализ графиков на рис. 9 и 10 позволяет сделать вывод, что углы продольного наклона корпуса при преодолении эскарпа в случае управляемой подвески снизились в два раза по сравнению с неуправляемой подвеской.
Заключение
В работе впервые предложен алгоритм управления подвеской МКМ, который обеспечивает повышение профильной проходимости многоосных колесных машин при преодолении эскарпа. Основными достоинствами алгоритма являются:
· снижение нагрузок на раму при преодолении крупных эскарпов;
· автоматическое управление подвеской, что означает, что водитель не участвует в процессе управления системой подрессоривания, выполняя лишь свойственные ему функции управления скоростью и направлением движения.
Предложенный алгоритм с успехом может быть использован при разработке управляемых систем подрессоривания перспективных транспортно-технологических комплексов на базе МКМ.
Список литературы
- Платонов С.В. Формирование скоростного режима движения автомобиля // Динамика колесных и гусеничных машин: Межвузовский тематический сб. – Волгоград, 1980. – С. 28 – 34.
- Белоусов Б.Н., Попов С.Д. Колесные транспортные средства особо большой грузоподъемности. Конструкция. Теория. Расчет. / Под общ. ред. Б.Н. Белоусова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 728 с.
- Аксёнов П.В. Многоосные автомобили. – М.: Машиностроение, 1980. – 208 с.
- Проектирование полноприводных колесных машин: Учебник для вузов: В 3 т. Т.3 / Б.А. Афанасьев, Б.Н. Белоусов, Л.Ф. Жеглов и др.; Под ред. А.А. Полунгяна. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. – 432 с.
Публикации с ключевыми словами: управление подвеской многоосных колесных машин, единичные неровности, эскарп
Публикации со словами: управление подвеской многоосных колесных машин, единичные неровности, эскарп
Смотри также:
- 77-30569/347098 Разработка статического алгоритма управления подвеской многоосных колесных машин: автоматизированное преодоление траншеи
- 77-30569/293578 Методика подбора характеристик управляемой подвески с двумя уровнями демпфирования многоосных колесных машин
- 77-30569/347783 Сравнительный анализ эффективности работы непрерывной и релейной систем управления подвеской многоосных колесных машин
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



