научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2012
УДК 681.5
МГТУ им. Н.Э. Баумана
Одной из задач, решаемых интеллектуализированной системой управления [1-3], является идентификация модели движения центра масс. Для сокращения объема необходимой памяти бортовой вычислительной машины и сокращения затрат машинного времени необходима унификация методов решения различных задач.
Под идентификацией модели движения центра масс ракет космического назначения (РКН) понимается оценка ее параметров по информации о характере полета РКН и некоторых ее характеристиках, получаемых с помощью бортовых измерительных средств.
Представим систему уравнений движения центра масс РКН в следующем виде:
![]() (1)
(1)
где ![]() - вектор фазовых координат,
- вектор фазовых координат,
t - время,
![]() (2)
(2)
V – вектор скорости,
r - радиус-вектор,
c - вектор параметров, характеризующих РКН и условия ее полета;
![]() (3)
(3)
![]() - вектор параметров потенциала поля земного тяготения U;
- вектор параметров потенциала поля земного тяготения U;![]() - вектор кажущихся ускорений центра масс РКН,
- вектор кажущихся ускорений центра масс РКН,
![]() (4)
(4)
Модель движения центра масс РКН будет полностью определена, если задан составной вектор ![]() ее параметров
ее параметров ![]() и начальных
и начальных ![]() , либо конечных
, либо конечных ![]() значений фазовых координат. Задача определения вектора
значений фазовых координат. Задача определения вектора ![]() параметров модели движения центра масс РКН относится к разряду задач параметрической идентификации систем.
параметров модели движения центра масс РКН относится к разряду задач параметрической идентификации систем.
Задача идентификации модели движения РКН сводится к задаче оценки вектора параметров ![]() модели и вектора
модели и вектора ![]() фазового состояния РКН в начальный или конечный момент времени по результатам измерений
фазового состояния РКН в начальный или конечный момент времени по результатам измерений ![]() - выхода системы (1)-(4), искаженного шумами и различного рода возмущающими факторами, действующими на исходную систему. Оценка
- выхода системы (1)-(4), искаженного шумами и различного рода возмущающими факторами, действующими на исходную систему. Оценка ![]() и
и ![]() (либо
(либо ![]() ) заключается в отыскании таких значений этих параметров, при которых выход
) заключается в отыскании таких значений этих параметров, при которых выход ![]() модели (1)-(4) наилучшим в некотором смысле образом приближался бы к выходу
модели (1)-(4) наилучшим в некотором смысле образом приближался бы к выходу ![]() реальной системы.
реальной системы.
В качестве выхода ![]() рассматриваемой системы (1)-(4) может использоваться либо вектор
рассматриваемой системы (1)-(4) может использоваться либо вектор ![]() кажущихся ускорений, либо вектор
кажущихся ускорений, либо вектор ![]() фазовых координат, либо оба этих вектора. В случае
фазовых координат, либо оба этих вектора. В случае ![]() идентификация системы (1)-(4) осуществляется по измерениям вектора кажущихся ускорений, в случае
идентификация системы (1)-(4) осуществляется по измерениям вектора кажущихся ускорений, в случае ![]() - по результатам решения навигационной задачи. При этом задача навигации может рассматриваться как частный случай идентификации системы (1) при
- по результатам решения навигационной задачи. При этом задача навигации может рассматриваться как частный случай идентификации системы (1) при ![]() и заданном значении параметров системы.
и заданном значении параметров системы.
Для оценки массово-энергетических характеристик РКН наряду с информацией о векторе кажущихся ускорений, получаемой с соответствующих измерителей (в частности, с акселерометров), может также использоваться информация о количестве топлива, получаемая с датчиков системы управления расходом топлива, и информация о давлении в камерах сгорания. В этом случае уравнение (1) дополнится соответствующими уравнениями связи
![]() (5)
(5)
где ![]() - измеренное количество топлива в баках;
- измеренное количество топлива в баках;![]() -измеренное значение давления в камере сгорания.
-измеренное значение давления в камере сгорания.
С помощью датчиков системы управления расходом топлива могут измеряться либо расходы топлива из баков, либо объемы компонентов топлива в баках Информация о давлении в камере сгорания может быть связана с расходом топлива с помощью дроссельной характеристики двигательной установки.
Пусть критерий ошибки приближения выхода модели к выходу реальной системы характеризуется функционалом
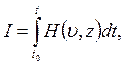 (6)
(6)
где H - скалярная положительно определенная мера ошибки.
Задача идентификации модели движения центра масс РКН заключается в определении таких векторов c,d и x0 , либо xk, которые минимизируют функционал (6) при условиях (1)–(4), т.е. в решении системы дифференциальных и функциональных уравнений
![]() (7)
(7)
![]() (8)
(8)
Если в уравнении (7) не учитываются аэродинамические члены, то уравнение (4) принимает вид
![]() (9)
(9)
в этом случае при ![]() для определения вектора
для определения вектора ![]() достаточно рассматривать уравнение (9), т.е. вектор
достаточно рассматривать уравнение (9), т.е. вектор ![]() будет определяться уравнениями:
будет определяться уравнениями:
![]() (10)
(10)
Если вектор c характеристик РКН известен или определен в результате решения задачи (7), (8), то при ![]() для определения вектора d параметров потенциала поля тяготения и вектора x0 фазового положения РКН может быть использована система уравнений
для определения вектора d параметров потенциала поля тяготения и вектора x0 фазового положения РКН может быть использована система уравнений
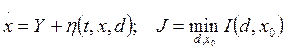 , (11)
, (11)
где вектор ![]() считается известным либо на основании измерений, либо на основании вычислений по формуле (4). В случае заданного значения вектора параметров
считается известным либо на основании измерений, либо на основании вычислений по формуле (4). В случае заданного значения вектора параметров ![]() приходим к задаче оценки x0 фазового состояния РКН в момент времени t0:
приходим к задаче оценки x0 фазового состояния РКН в момент времени t0:
 (12)
(12)
Если вектор ![]() считается известным в результате измерений, то при
считается известным в результате измерений, то при ![]() задача определения вектора фазового положения центра масс РКН сводится к задаче интегрирования уравнения
задача определения вектора фазового положения центра масс РКН сводится к задаче интегрирования уравнения
![]() (13)
(13)
которая представляет собой задачу навигации РКН. Интегрирование уравнения (13) на упрежденном отрезке времени при известном законе изменения вектора ![]() представляет собой задачу прогнозирования фазового положения центра масс РКН.
представляет собой задачу прогнозирования фазового положения центра масс РКН.
Таким образом, могут быть сформулированы следующие типы задач по определению параметров моделей движения центра масс РКН:
1.Идентификация динамической системы
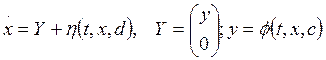 (14)
(14)
по информации о векторе ![]() , либо о векторе y или о векторах x и y. При этом информация о векторе x может быть получена в результате решения задачи навигации, а о векторе y - в результате измерения вектора кажущегося ускорения. В случае использования лишь информации о векторе x уравнение (14) эквивалентно системе уравнений
, либо о векторе y или о векторах x и y. При этом информация о векторе x может быть получена в результате решения задачи навигации, а о векторе y - в результате измерения вектора кажущегося ускорения. В случае использования лишь информации о векторе x уравнение (14) эквивалентно системе уравнений
![]() (15)
(15)
Если используется информация о векторах x и y, то можно ввести в рассмотрение расширенный вектор ![]() и соответствующее векторное уравнение
и соответствующее векторное уравнение
![]() (16)
(16)
где
 . (17)
. (17)
В этом случае задача формально сведена к типу задачи идентификации системы (15) по информации о векторе x.
2. Идентификация динамической системы
 (18)
(18)
по информации о векторе x, либо о векторе y, или о векторах x и y.
При использовании информации лишь о векторе х уравнение (18) эквивалентно системе уравнений
![]() (19)
(19)
По аналогии с предыдущим случаем задача идентификации модели (18) по информации о векторах x и y может быть сведена к типу задачи идентификации системы (19) по информации о векторе x.
3. Идентификация статической модели
![]() (20)
(20)
по информации о векторе y.
Идентификация динамической системы
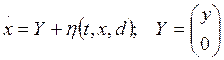 (21)
(21)
по информации о векторе x , где y - заданная вектор-функция.
При этом вектор y определяется либо в результате измерений кажущихся ускорений, либо с помощью функции (20) при известном векторе параметров c .
5.Определение значения вектора x в результате интегрирования уравнения
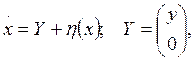 (22)
(22)
где y - заданная вектор-функция, определяемая либо в результате измерения вектора кажущихся ускорений (при решении задачи навигации РКН), либо с помощью заданных аналитических зависимостей (при решении задачи прогноза фазового состояния РКН).
В условиях высокой точности измерения параметров движения РКН и влияния стабильных по характеру изменения возмущений и погрешностей измерения от алгоритма идентификации требуется лишь выполнение роли алгоритма аппроксимации реального движения центра масс РКН некоторой его моделью и не требуется одновременного выполнения роли фильтра. В связи с этим ограничимся рассмотрением лишь детерминированных моделей движения центра масс РКН.
Основными составляющими правых частей уравнений движения центра масс на участке выведения КА являются тяга двигателей и гравитационное ускорение. При этом потери скорости на преодоление сопротивления воздуха и за счет донного сопротивления двигателей составляют порядка 10-15 % от скорости на выходе из плотных слоев атмосферы (примерно на высоте 100 км). В связи с этим аппроксимирующая модель реального движения РКН может не учитывать влияние атмосферы на движение его центра масс и для идентификации параметров модели достаточно использовать системы (20) и (21).
При идентификации моделей движения РКН может быть использована достаточно обширная априорная информация, полученная на этапах создания и отработки РКН. В частности, известно, что пределы разброса массово-энергетических и аэродинамических характеристик РКН не превосходят соответственно 1-3 % и 10-15 % от их номинальных значений. Поэтому для уточнения такого рода характеристик могут использоваться линейные аппроксимации рассмотренных выше динамических и статических систем.
В качестве меры ошибки аппроксимации вектор-функции z(t) измерений кривой ![]() может быть выбрана квадратичная форма
может быть выбрана квадратичная форма
 (23)
(23)
где R - матрица весовых коэффициентов.
В принципе мерой ошибки ![]() может служить также норма
может служить также норма ![]() вектора
вектора ![]() , либо скалярное произведение
, либо скалярное произведение ![]() . Если квадрат нормы и скалярное произведение определены через сумму квадратов компонент вектора, то мера ошибки эквивалентна записи (23) при R=E.
. Если квадрат нормы и скалярное произведение определены через сумму квадратов компонент вектора, то мера ошибки эквивалентна записи (23) при R=E.
Для решения сформулированных задач идентификации детерминированных моделей движения центра масс РКН могут быть использованы разнообразные методы поиска минимума функции (6), как аналитические, так и численные. Аналитические методы базируются на теории оптимального управления системами, и, как правило, сводят задачу идентификации к проблеме двухточечной краевой задачи. Численные методы базируются на теории нелинейного программирования и зачастую сводятся к различного рода градиентным процедурам.
Переход к двухточечной краевой задаче.
Если правые части динамической системы
![]() (24)
(24)
модели наблюдения
![]() (25)
(25)
и подынтегральная функция функционала
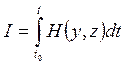 (26)
(26)
являются гладкими функциями своих переменных, а система (24)-(25) являются идентифицируемой, то задача минимизации функционала (26) при условии (24) с помощью коэффициентов Лагранжа может быть сведена к задаче на безусловный экстремум функционала
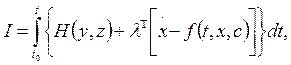 (27)
(27)
где ![]() -вектор множителей Лагранжа.
-вектор множителей Лагранжа.
Интегрируя (27) по частям и приравнивая первую вариацию функционала нулю, с учетом явной зависимости вектора ![]() от вектора
от вектора ![]() и вектора начальных состояний
и вектора начальных состояний ![]() получим следующие соотношения для оптимальных значений искомых параметров
получим следующие соотношения для оптимальных значений искомых параметров ![]() и x0:
и x0:
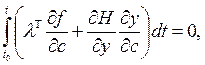 (28)
(28)
 (29)
(29)
Таким образом, задача идентификации системы (24) адекватна двухточечной краевой задаче для системы уравнений (24) и (29) при интегральных связях (28) и нулевых значениях переменной ![]() на концах. Для определения векторов c размерности m, вектора x0 размерности n и вектор-функции
на концах. Для определения векторов c размерности m, вектора x0 размерности n и вектор-функции ![]() размерности n получено 2n+m соотношений (24), (28), (29) и 2n краевых условий
размерности n получено 2n+m соотношений (24), (28), (29) и 2n краевых условий ![]() . Интегральные связи (28) при условиях на концах
. Интегральные связи (28) при условиях на концах ![]() и
и ![]() могут быть заменены эквивалентными дифференциальными связями
могут быть заменены эквивалентными дифференциальными связями
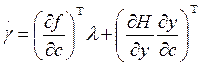 . (30)
. (30)
Если не использовать множители Лагранжа, то оптимальные значения векторов c и x0 определяются из условия равенства нулю вариации функционала (26), т.е. из соотношения
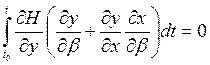 (31)
(31)
при 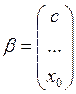 и условиях (24) и (25).
и условиях (24) и (25).
Производные ![]() могут быть определены с помощью уравнений чувствительности
могут быть определены с помощью уравнений чувствительности
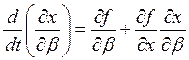 (32)
(32)
при 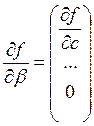 и условиях
и условиях ![]()
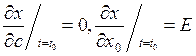 .
.
Интегральное уравнение (31) может быть заменено эквивалентным дифференциальным уравнением
 (33)
(33)
при условиях на концах ![]()
Для определения вектора ![]() размерностью
размерностью ![]() имеется всего
имеется всего ![]() соотношений. При этом на каждом шаге итерации приходится интегрировать на
соотношений. При этом на каждом шаге итерации приходится интегрировать на ![]() уравнений больше, чем в методе, использующем множители Лагранжа.
уравнений больше, чем в методе, использующем множители Лагранжа.
Условия стационарности (24), (29) и (30) можно также получить, если ввести в рассмотрение векторное уравнение
![]() (34)
(34)
и использовать методы теории оптимального управления систем [4].
Если начальные условия ![]() заданы, то для уравнения (29) левый конец является свободным и двухточечная краевая задача для системы (24), (29) и (30) решается при условиях
заданы, то для уравнения (29) левый конец является свободным и двухточечная краевая задача для системы (24), (29) и (30) решается при условиях ![]()
Рассмотрим возможности решения краевой задачи для уравнений (24), (29) и (30), которые могут быть записаны в следующем каноническом виде:
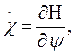 (35)
(35)
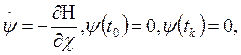 (36)
(36)
где ![]() - гамильтониан,
- гамильтониан, 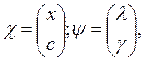
![]() (37)
(37)
Для наиболее важных для практики линейных систем
![]() (38)
(38)
![]() (39)
(39)
и квадратичной меры ошибки приближения
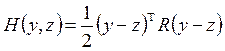 (40)
(40)
уравнения (29) и (30) принимают вид
![]() (41)
(41)
![]() (42)
(42)
где ![]() - матрицы.
- матрицы.
Решение краевой задачи (24), (29) и (30) либо (38)-(42) заключается в отыскании таких параметров c и x0, которые обращают в ноль невязки ![]() и
и ![]() в момент
в момент ![]() .
.
Анализ методов решения двухточечных краевых задач достаточно подробно проведен в ряде работ. В целом, рассмотренные методы решения краевых задач являются достаточно общими и практически не учитывают специфику идентифицируемой системы. Линейные системы обладают характерными особенностями, вытекающими из существования фундаментальных решений, сопряженных переменных и свойств скалярных произведений фазовых и сопряженных переменных, которые могут быть использованы при разработке методов идентификации этих систем.
В частности, показано, что при идентификации линейных систем методом сопряженных уравнений двухточечная краевая задача для уравнений (38), (41) и (42) может быть сведена к решению системы линейных алгебраических уравнений
 (43)
(43)
![]()
где переменные ![]() , определяются соответственно уравнениями
, определяются соответственно уравнениями
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
Уравнения (44) и (45) могут быть проинтегрированы в обратном времени при начальных условиях ![]() и
и
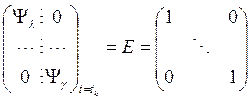 , (47)
, (47)
где ![]() - матрица фундаментальных решений, а интегралы в соотношении (43) могут определяться с помощью уравнений
- матрица фундаментальных решений, а интегралы в соотношении (43) могут определяться с помощью уравнений
![]()
![]() (48)
(48)
![]() , (49)
, (49)
интегрируемых при нулевых начальных условиях.
Если известна матрица фундаментальных решений X(t,t0) уравнения (38), то с учетом того, что матрица фундаментальных решений уравнения (41) равна ![]() , а граничные значения переменных
, а граничные значения переменных ![]() и
и ![]() равны нулю, уравнения для определения параметров xo и c примут вид
равны нулю, уравнения для определения параметров xo и c примут вид
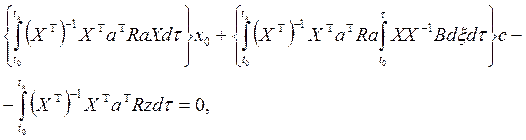 (50)
(50) (51)
(51)
Следует отметить, что общее решение уравнения (38) равно
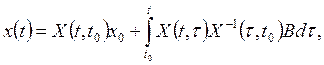 (52)
(52)
для которого можно записать эквивалентное уравнение типа уравнения Вольтерра для фундаментальной матрицы, ограничившись рассмотрением лишь первого приближения
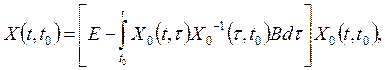 (53)
(53)
где E- единичная матрица,
 (54)
(54)
При достаточно малом интервале [t,t0]
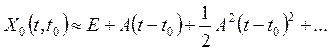 (55)
(55)
Для случая линейной стационарной системы ![]() и квадратичной меры приближения (40) может быть использовано условие
и квадратичной меры приближения (40) может быть использовано условие ![]()

откуда с учетом y=bc получаем:
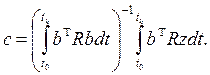 (56)
(56)
Для решения уравнения (56) либо краевой задачи для уравнений (24), (29) и (30) могут быть использованы разнообразные численные методы.
Таким образом, задача идентификации сведена к двухточечной краевой задаче, что позволяет унифицировать программно-алгоритмическое обеспечение интеллектуализированной системы управления при формировании базы знаний.
Литература
1. Пролетарский А.В. Управление полетом ракет космического назначения. М.: Издательство МГОУ, 2006. 140с.
2. Пролетарский А.В., Неусыпин К.А., Цибизова Т.Ю. Системы управления летательными аппаратами и алгоритмы обработки информации. М.: Издательство МГОУ, 2006. 220с.
3. Пролетарский А.В. Интеллектуализированная система управления перспективными ракетами космического назначения. Автоматизация и современные технологии, 2011, №6, с. 30-33
Публикации с ключевыми словами: идентификация, ракета космического назначения, модель движения
Публикации со словами: идентификация, ракета космического назначения, модель движения
Смотри также:
- Исследование напряженно-деформированного состояния стартово-стыковочного блока для перспективной ракеты тяжелого класса
- Идентификация нелинейных динамических систем, имеющих в своём составе несколько нелинейностей
- Анализ и моделирование штатных и нештатных нагрузок и воздействий на агрегаты стартовой системы для РКН семейства «Союз»
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



