научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2012
УДК.67.02 , 004.942, 519.178
МГТУ им.Н.Э. Баумана
Вопросам проектирования технологии сборки уделяется большое внимание в машиностроении. От рационального выбора последовательности сборки деталей в сборочные единицы зависит удобство и качество сборки, временные и стоимостные затраты выполнения сборочного технологического процесса. Проблема состоит в том, что число возможных вариантов сборочной технологии существенно зависит от числа деталей на сборочном чертеже. Так, при числе деталей в составе сборочной единицы N=15 число вариантов последовательностей сборки без учета геометрических, технологических и прочих ограничений, составит N! = 1,3*Е+12. Поэтому автоматизация проектирования сборочных технологических процессов является актуальной задачей.
Одним из эффективных методов решения такой задачи является применение теории графов с целью минимизации расчетных ресурсов [1-5, 7-13]. Например, в работах [1-3] описано использование графа для построения взаимосвязей между элементами конструкции и формирования на этой основе сборочной технологии. При таком построении модели изделия сложно учитывать многочисленные связи в конструкции. Использование в моделях конструкций математического механизма гиперграфов позволило формировать последовательности сборки изделия, учитывающие всю полноту механических связей деталей в конструкции [4, 5]. При этом в моделях изделий учитываются условия контакта деталей, базирования деталей друг относительно друга, возможности группирования деталей в узлы.
В данной работе предлагается метод формирования совокупности допустимых вариантов сборочного технологического процесса изделия, который позволяет создавать последовательность сборки, учитывая ограничения различной природы, предполагающих невозможность сборки. Основным отличием предлагаемого метода от модели гиперграфа механических связей [4], является описание именно невозможности сборки, что позволяет при генерации упростить и ускорить механизм отбора вариантов сборки. Помимо этого, в предлагаемом методе учитываются технологические, организационные и экономические ограничения, возникающие при сборке определенных конструкций. Поясняющий пример основан на выборе последовательности сборки упрощенного кумулятивного заряда.
В работах [6, 7] изложены научные основы методики проектирования технологических процессов для изготовления кумулятивных зарядов. Применительно к сборочным процессам предложено наряду с традиционными гиперграфами [3-5] использовать теорию ориентированных гиперграфов с ограничениями [12], что при проектировании позволяет обеспечивать просмотр и анализ значительно большего числа вариантов сборки изделия, по сравнению с обычным путем проектирования. Рассматриваемый метод основан на введении разработчиком ограничений на возможные варианты сборки изделия, определяющих возможность или невозможность последующей сборки. Метод является более компактным при использовании вычислительных ресурсов, по сравнению с традиционными моделями.
Предполагая, что имеются М шагов (технологических операций), на каждом из которых имеется Nвариантов выбора (количество деталей и сборочных единиц), можно определить число вариантов выбора - МN . Большинство из них будут недопустимыми по геометрическим (конструктивным), технологическим, экономическим и прочим ограничениям. При проектировании последовательности сборки количество вариантов сборки составляет N!. На практике разработчик строит несколько вариантов проектного решения и по определенным критериям выбирает из них. Поскольку анализируются не все допустимые решения, можно говорить только о выборе лучшего из предложенного, но не об оптимальном варианте. Если генерировать множество допустимых проектных решений автоматически, или с минимальным вмешательством разработчика, то возможно обеспечить просмотр и анализ значительно большего числа проектных решений за приемлемое время. В работе предлагается один из возможных методов решения этой задачи, основанный на понятии «гиперграф ограничений».
Гиперграф отличается от обычного графа тем, что связи на нем соединяют несколько (не обязательно две) вершин. В ориентированном гиперграфе множество вершин, соответствующих какой-либо связи делится на множество входных вершин и множество выходных вершин. Таким образом, гиперграф задается множеством вершин N(собираемых деталей) и множеством связей М (сборочных операций), где каждая связь m∈M есть пара m= <T,R>, T⊆N и R⊆N, где T – множество входных вершин, R – множество выходных вершин. Подробно математическое описание ориентированных гиперграфов и их отличия от других моделей изложены в [9-11], в настоящей работе описывается их конкретное применение к задаче проектирования технологических процессов сборки. Ориентированный гиперграф ограничений может быть представлен в общем виде набором входных, выходных вершин и гиперсвязей (рис. 1). К множеству вершин Nотносятся вершины (детали) 1,2,…i-1,i,i+1,…N-1,N, входящие в сборочный чертеж агрегата или изделия; к множеству связей Mотносятся гиперсвязи A, B, C, D, E, F…; к множеству входных вершин Т относятся вершины 1, 2, 3, 4, 5, i-1, N-1, N (от этих вершин направлены гиперсвязи); к множеству выходных вершин Rотносятся вершины 2, 3, 5, i, i+1 (к этим вершинам направлены гиперсвязи; множество входных и выходных вершин может пересекаться). Например, гиперсвязь (ограничение) А =<{1, 2},{5}> означает, что при сборке детали 1 с деталью 2 деталь 5 не сможет быть установлена совсем и останется «лишней», причем порядок сборки {1, 2} или {2, 1} значения не имеет. Не получится собрать изделие и при таких вариантах, когда между деталями – входными вершинами гиперграфа и выходными вершинами в последовательности сборки устанавливается другая деталь, например вышеуказанное ограничение запретит варианты сборки 1425, 4231i5, т.е. те, в которых деталь 5 устанавливается после деталей 1 и 2. Следует отметить, что последовательность сборки гиперграфом ограничений никак не отображается – ограничения необходимы для отсечения вариантов невозможности сборки при генерации. В упрощенном виде, каждая гиперсвязь интерпретируется следующим образом: «если ранее были выбраны варианты T, выбор вариантов из R запрещен – сборка невозможна».
Гиперсвязь (ограничение) С =<{N-1, N},{2}> означает, что если будут собраны детали с номерами N-1 и N до установки детали 2, то деталь 2 не сможет быть установлена совсем и останется также «лишней». Подобным образом трактуются и остальные гиперсвязи.
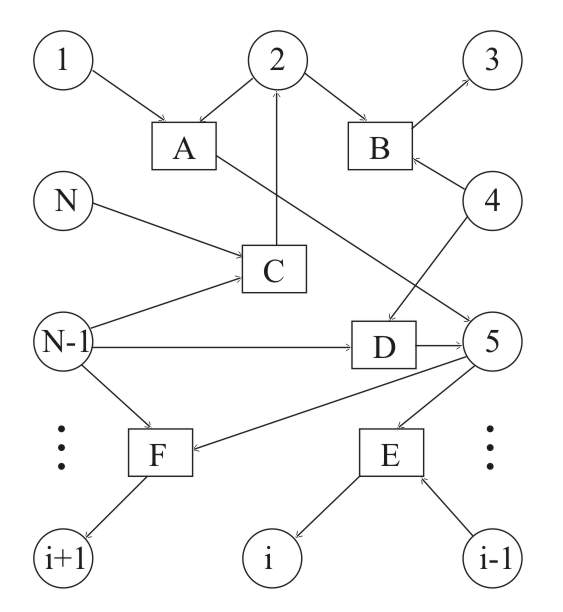
Рис. 1. Ориентированный гиперграф ограничений
Разработчик технологии сборки формирует систему ограничений исходя из различных условий: геометрии изделия, доступных технологических методов, физических, экономических предпосылок и т. п. Алгоритм генерации строит полное множество последовательностей решений, проверяя на каждом шаге список ограничений и отвергая наборы решений, запрещенные хотя бы одной гиперсвязью.
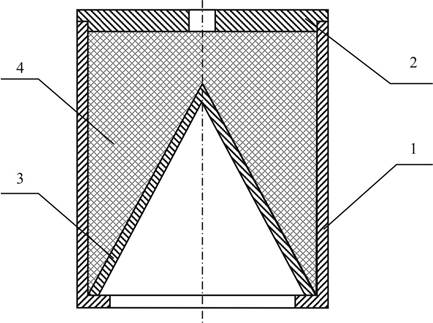
Рис. 2. Конструкция условного изделия «заряд». 1 - корпус, 2 - крышка, 3 – облицовка, 4 - шашка.
Рассмотрим генерацию вариантов сборочного процесса для условного изделия «заряд» (рис. 2). Геометрические (конструктивные) ограничения на сборку этого изделия описываются 4-мя ограничивающими гиперсвязями (рис. 3):
А= <{1, 2},{3}> (собранные вместе корпус 1 и крышка 2 не позволят установить облицовку 3), B=<{1, 2},{4}> (собранные вместе корпус 1 и крышка 2 не позволят установить шашку 4), C=<{1, 4},{3}> (собранные вместе корпус 1 и шашка 4 не позволят установить облицовку 3) , D=<{2, 3},{4}> (собранные вместе крышка 2 и облицовка 3 не позволят установить шашку 4).
Без учета ограничений, имеется N! последовательностей сборки (24 последовательности). Алгоритм генерации последовательностей сборки с учетом введенных ограничений сгенерирует только 8 допустимых последовательностей (рис. 4) [12]. На рисунке 4 затененные шаги соответствуют выполненным шагам алгоритма, незатененные шаги алгоритм отверг, используя ограничения.
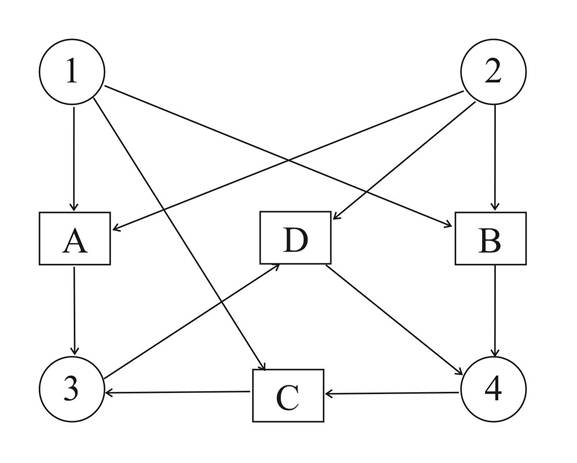
Рис. 3. Ориентированный гиперграф геометрических ограничений для изделия «заряд».
Следует отметить, что некоторые варианты могут быть нерациональны, поскольку задавались только геометрические ограничения, хотя существуют и технологические, физические. Задав, например, дополнительную гиперсвязь: Е=<{},{3}>, будут исключены варианты сборки, начинающиеся с детали 3 («облицовка»).
Вместе с тем, определение ориентированного гиперграфа не исключает случаев пустого входного или выходного множества вершин у гиперсвязи. Такая связь в гиперграфе ограничений трактуется как запрет выбора варианта при пустом множестве ранее принятых решений.
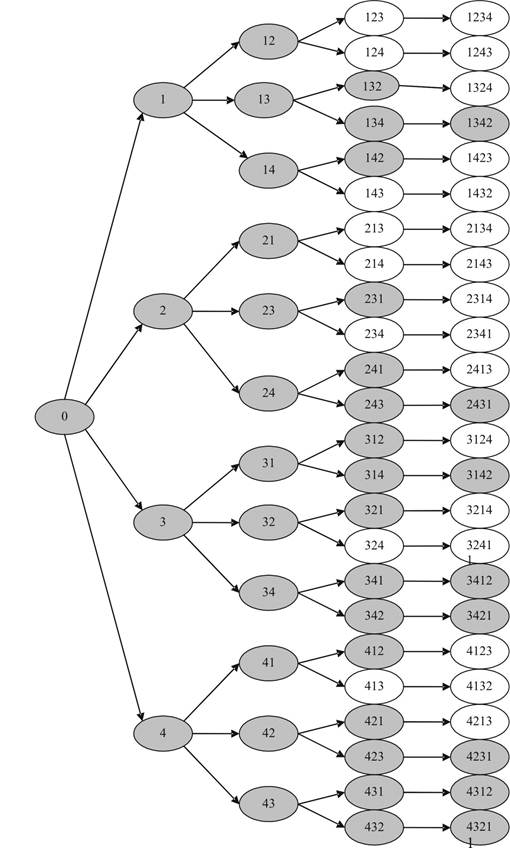
Рис. 4. Дерево вариантов сборочного процесса изделия «заряд».
Рассмотрим основные задачи, возникающие при реализации метода:
· Формирование гиперграфа ограничений,
· Проверка непротиворечивости системы введенных ограничений,
· Проектирование и оптимизация алгоритма генерации решений,
· Задание целевой функции для выбора оптимального проектного решения.
Описывая формирование гиперграфа ограничений, следует отметить, что одним из преимуществ модели, основанной на ограничениях, является ее простота и экономичность. При прямом проектировании процессов выбор проводится в пространстве решений N!, анализируя цепочки решений (для «заряда» - 24 решения). При формировании графа ограничений анализируется пространство размерности N и описываются отдельные, не связанные в цепочки, ограничения, что связано со смысловой природой ограничений - их независимостью друг от друга (в рассматриваемом примере число решений с учетом ограничений 2∙N= 8). Систему ограничений несложно корректировать, ограничиваясь локальными изменениями на графе, при этом добавление нового ограничения сводится к добавлению гиперсвязи. При этом не требуется перегенерации вариантов решений, достаточно оценить ранее найденные варианты на дополнительное ограничение. Допустима динамическая вставка новых ограничений во время работы алгоритма генерации. При создании средств автоматизации проектирования ограничений следует упростить задачу проектировщика, предусмотрев возможность проектировать гиперсвязь последовательностью щелчков мыши на чертеже изделия или списках деталей. Дополнительный эффект дает наличие библиотеки шаблонов гиперграфов ограничений, соответствующих типовым узлам проектируемой конструкции или типовым технологическим ограничениям (сборка неразъемных соединений, операции нанесения покрытий и пр.).
Следующим этапом метода является проверка непротиворечивости системы введенных ограничений. Гиперграф ограничений считается непротиворечивым, если на его базе может быть сгенерировано хотя бы одно допустимое проектное решение. Проверка непротиворечивости осуществляется прогоном алгоритма генерации, но, в связи с продолжительностью его работы (вследствие большого объема данных), необходима предварительная оценка системы ограничений. Такая проверка фиксирует противоречивые связи, локализуя места необходимых изменений. В алгоритме проверки должны быть запрещены циклы на гиперграфе ограничений. Создание максимально полной системы критериев проверки непротиворечивости – задача дальнейших исследований.
После проверки непротиворечивости проводится проектирование и оптимизация алгоритма генерации решений. В своей основе алгоритм генерации сводится к следующему. Формируются два множества: множество принятых вариантов решений P={} и множество оставшихся вариантов решений Е=N.
На каждом шаге выбирается элемент n∈E. Просматривается гиперграф ограничений. Если существует гиперсвязь m= <T,R>, такая, что T⊆P и n∈R (вариант недопустим), выбирается следующий элемент из Е, иначе (вариант допустим) элемент n переносится в P и шаг повторяется. Если P=N, фиксируется допустимый вариант проектного решения.
Если все элементы из Е перебраны или Р=N, элемент, записанный в P на предыдущем шаге переносится обратно в Е и выбирается следующий элемент из Е. Процесс заканчивается, если переносимый обратно в Е элемент – последний в N и Р – множество из одного элемента.
Хотя, благодаря отсечению недопустимых вариантов, многие «кусты» дерева вариантов не исследуются, алгоритм, потенциально, является NP – полным. Поэтому важное значение имеет оптимизация алгоритма.
Предлагаемый метод генерации проектных решений напрямую не связан с выбором и наличием целевой функции – он создает множество допустимых проектных решений. Поэтому возможно применение любой целевой функции для дальнейшей оценки вариантов. Однако, если целевая функция используется не по окончанию процесса генерации, а внутри него на шагах генерации, она должна отвечать некоторым условиям. В целом эти условия аналогичны требованиям к целевой функции для метода ветвей и границ и в данной работе подробно не рассматриваются.
Рассмотрим использование гиперсвязей с ингибиторами, при которых множества входных вершин и выходных вершин разбиваются, каждое, на два подмножества:
m= <T,ТI,R,RI>, T⊆N и R⊆N, TI⊆N и RI⊆N, где TI , RI– множества ингибиторов. Пример графического отображения гиперсвязи с ингибиторами в виде стрелки с малой окружностью приведен на рис.5.

Рис. 5. Пример гиперсвязи с ингибиторами F=<{3},{4’},{2},{}>.
Содержательная трактовка гиперсвязи с ингибиторами реализует логику ограничений с отрицаниями. Так, для нашего примера сборки F=<{3},{4’},{2},{}> (4’ – гиперсвязь с ингибитором), приведенная гиперсвязь трактуется так:
«Если установлена облицовка 3 и НЕ установлена шашка 4, нельзя установить крышку 2».
Связи с ингибиторами позволяют расширить логику системы ограничений. В частности, они позволяют задавать «прямое» проектирование некоторого варианта сборки. Так, для жесткого определения варианта сборки 1342, достаточно задать ограничения (рис. 6):
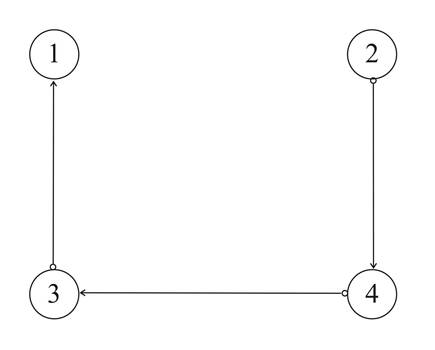
Рис. 6. Система ограничений для задания варианта сборки заряда 1342.
Для корректного описания технологии сборки предложено разделить ограничения на виды: конструктивные, технологические, организационные, экономические. К конструктивным ограничениям относят геометрические ограничения, которые не позволяют в собранный контур узла установить деталь узла, расположенную внутри (рис. 2, 3). К технологическим ограничениям относят сборку неразъемных соединений (сварку, пайку и т.д.), операции нанесения покрытий (теплозащитных, антикоррозионных), необходимость проведения испытаний для собранного узла на определенном этапе изготовления (испытания на прочность, герметичность, электрические испытания), операции совместной механической обработки узла в сборе (подрезка торцов, сверление отверстий). Отмечено, что на технологические ограничения помимо геометрии влияет набор технических требований к изделию. Такой широкий спектр ограничений требует, в целом, более подробной классификации. Организационные и экономические ограничения определяются типом производства (единичное, серийное, массовое), степенью проработки технологии для каждого из типов производства, возможностью автоматизации части сборочных операций.
Рассмотрим пример формирования технологических ограничений гиперграфа для изделия «заряд». При наличии в конструкции изделия (рис. 7) деталей с покрытиями, или указания способа соединения (в примере - склеивание), которые не отражаются в спецификациях сборочных чертежей, а указываются в технических требованиях к изделию, модель изделия должна быть дополнена новыми элементами, имитирующими псевдодетали, но отражающими ограничения гиперграфа. В изделии «заряд» крышка 2 соединяется с корпусом 1 резьбой, но при этом торец корпуса промазывается клеем-герметиком 5, облицовка 3 устанавливается в корпус на слой клея-герметика 6. На внутреннюю поверхность корпуса 1 наносится специальное покрытие 7.
Для этого случая гиперграф технологических ограничений с ингибиторами, дополнительный к изображенному на рис. 3, будет описан следующим образом (рис. 8):
G=<{1},{5’},{2},{}> (Если установлен корпус 1 и не установлена герметичная прокладка 5, нельзя устанавливать крышку 2);
H=<{1},{6’},{3},{}> (Если установлен корпус 1 и не установлена герметичная прокладка 6, нельзя устанавливать облицовку 3);
J=<{1},{7’},{4},{}> (Если установлен корпус 1 и на него не нанесено специальное покрытие 7, нельзя устанавливать шашку 4).
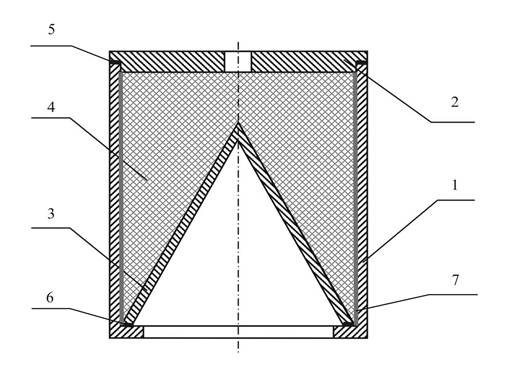
Рис. 7. Конструкция условного изделия «заряд» с учетом покрытия и герметизации. 1 - корпус, 2 - крышка, 3 – облицовка, 4 – шашка, 5,6 – клей-герметик, 7 – специальное покрытие.
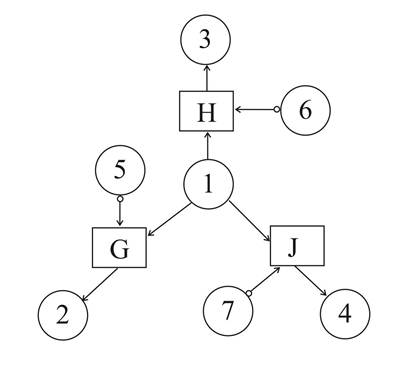
Рис. 8. Ориентированный гиперграф технологических ограничений изделия «заряд».
Организационные и экономические ограничения возможно описывать как обычными гиперсвязями, так и гиперсвязями с ингибиторами.
Таким образом, в статье предложен метод, основанный на применении ориентированных гиперграфов ограничений, позволяющий существенно сократить трудоемкость решения задач формирования совокупности допустимых проектных решений сборочной технологии, показаны его основные возможности на примере проектирования вариантов сборки кумулятивного заряда, описаны основные виды ограничений и способы их графического отображения.
Литература
1. Автоматизация проектирования технологических процессов в машиностроении. В.С. Корсаков, Н.М. Капустин, К.-Х. Темпельгоф и др. М.: Машиностроение, 1985. 304 с.
2. Технология сборки самолетов. В.И. Ершов, В.В. Павлов и др. М.: Наука,1986. 456 с.
3. Информационно-вычислительные системы в машиностроении CALSтехнологии. Ю.М. Соломенцев , В.Г. Митрофанов, В.В. Павлов и др. М.: Наука, 2003. 292 с.
4. Божко А.Н. Выбор рациональной последовательности сборки изделия // Электронное научно-техническое издание «Наука и образование» – 2010. – №7.
5. Божко А.Н. Моделирование механических связей изделия // Электронное научно-техническое издание «Наука и образование» – 2011. – №3.
6. В.А. Тарасов, В.Д. Баскаков, П.В. Круглов. Методика проектирования технологии изготовления высокоточных деталей боеприпасов //Оборонная техника, 2000, №1-2. с. 89-92.
7. В.А. Тарасов, В.Д. Баскаков, П.В. Круглов. Научные основы проектирования технологии изготовления прецизионных кумулятивных зарядов // Экстремальные состояния вещества. Детонация. Ударные волны. III Харитоновские тематические научные чтения: Труды международной конференции. -Саров, 2002., С. 254-257.
8. Г.Б. Евгенев. Интеллектуальные системы проектирования. М.: Изд-во МГТУ им. Н.Э. Баумана, 2009.- 334 с.
9. А.И. Белоусов, А.В. Пастуховский Ориентированные гиперграфы и системы подстановок. // Фундаментальная и прикладная математика. 1996, 2, № 4, С. 1163-1186.
10. Зыков А.А. Гиперграфы. // Успехи математических наук 1974, № 6, С. 89-154.
11. Горбатов В.А. Основы дискретной математики. М.: Высшая школа 1986, 311 с.
12. В.А. Тарасов, П.В. Круглов, А.В. Пастуховский. Применение ориентированных гиперграфов для проектирования технологии сборки зарядов. // Экстремальные состояния вещества. Детонация. Ударные волны. ХI Харитоновские тематические научные чтения: Труды международной конференции. -Саров, 2009., С. 743-748.
13. В.В. Павлов. Некоторые особенности АСТПП в производстве сложных изделий //Автоматизация технологической подготовки на основе ЕСТПП. М.: Издательство стандартов, 1976, с. 152.
Публикации с ключевыми словами: сборка, последовательность сборки, ориентированный гиперграф, выбор вариантов сборки
Публикации со словами: сборка, последовательность сборки, ориентированный гиперграф, выбор вариантов сборки
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



