научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2012
УДК 621.37
МГТУ им. Н.Э. Баумана
Постановка задачи
Воздействие гармонических помех на фазовую автоподстройку (ФАП) много лет привлекает внимание исследователей [1-12]. Первой работой в этом направлении является статья Журавлева А.Г. [1], посвященная экспериментальному исследованию воздействия гармонических помех на ФАП. Им выявлены условия захвата за сигнал и за помеху. В работе [2] предпринята попытка аналитического исследования, но лишь при нулевой начальной расстройке сигнала и управляемого генератора на основе метода гармонического баланса. С использованием этого метода в [3, 4] получен ряд динамических характеристик ФАП. В статье [5] приводится анализ ФАП при гармонической помехе на входе численным методом с использованием метода фазовой плоскости, и c учетом начальной расстройки по частоте двух колебаний. В [6] исследование проводится методом усреднения. В работах [7-9] с учетом начальной расстройки между частотами сигнала и управляемого генератора приближенным методом получен ряд динамических характеристик ФАП в зависимости от интенсивности помехи и параметров ФАП первого и второго порядков.
В книге автора [7] ФАП исследовалась методом гармонического баланса, когда предполагаемое решение дифференциального уравнения (ДУ) ФАП [7]
![]() (1)
(1)
принималось в виде
![]() (2)
(2)
В (1) ![]() - оператор дифференцирования;
- оператор дифференцирования; ![]() t1,c – время; Ω – полоса синхронизации ФАП;
t1,c – время; Ω – полоса синхронизации ФАП; ![]()
![]() - расстройка по частоте между частотой сигнала
- расстройка по частоте между частотой сигнала ![]() и частотой управляемого генератора
и частотой управляемого генератора ![]()
![]() - расстройка по фазе помехи и сигнала;
- расстройка по фазе помехи и сигнала; ![]()
![]() - соответствующая расстройка по частоте;
- соответствующая расстройка по частоте; ![]() - отношение амплитуд помехи и сигнала; F(p) – передаточная функция фильтра в кольце ФАП.
- отношение амплитуд помехи и сигнала; F(p) – передаточная функция фильтра в кольце ФАП.
Параметры предполагаемого решения (2): постоянная составляющая x0, амплитуда первой гармоники x1 и фазовый угол ψ в [7] находились в процессе гармонического баланса при условии малого значения амплитуды x1 и при условии d > 1, что обусловило использование приближенных соотношений [7].
![]()
(3)
![]()
В данной статье при использовании ДУ (1) и предполагаемого решения в форме (2) используется более строгий подход, когда вместо (3) используются приближения более высокого порядка, в связи с чем повышается точность получаемых результатов: динамических характеристик и критических значений параметров ФАП и помехи. Кроме того, производится сравнение критических значений параметров ФАП, получаемых методом гармонического баланса и методом фазовой плоскости [5, 8].
1. Основные соотношения
При использовании предполагаемого решения ДУ в виде (2) в правой части ДУ (1) получим
![]()
Воспользуемся известными разложениями

где Jn(z) – функция Бесселя n-го порядка.
Используем приближенные равенства, вытекающие отсюда при сохранении лишь первых слагаемых,

Тогда получим,
![]() (4)
(4)
Далее используем разложение второго слагаемого в квадратных скобках (1),
![]() .
.
где sinx по (4), а
![]() (5)
(5)
Подставляя приближенные значения слагаемых в квадратных скобках в правой части ДУ (1), после дифференцирования процесса в левой части ДУ (1), получим приближенное соотношение, из которого в дальнейшем находятся постоянная составляющая x0, амплитуда первой гармоники x1 и фазовый угол ψ.
Предварительно положим
![]() (6)
(6)
причем ![]()
Тогда подставляя (2) в ДУ (1) с учетом (4), (5), (6) получим соотношение
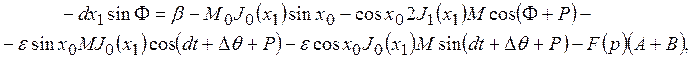 (7)
(7)
где 
так как при этом отброшены вторые гармоники ![]() и
и ![]()
Аналогично получим
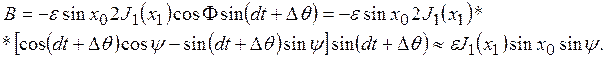
В сумме находим
![]()
Таким образом,
![]()
Следовательно, баланс по постоянным составляющим приводит к соотношению
![]() (8)
(8)
Отсюда,используя приближенные равенства
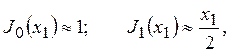 (9)
(9)
получим [7, ф-ла (12.20)].
Далее осуществим гармонический баланс оставшихся слагаемых в (7).
Слева в (7) находим
![]()
Приравнивая коэффициенты при ![]() и
и ![]() слева и справа в (7), получим соотношения, определяющие искомые значения x0, x1, ψ.
слева и справа в (7), получим соотношения, определяющие искомые значения x0, x1, ψ.

(10)
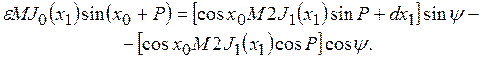
Отсюда при условиях (9) приходим к приближенным соотношениям [7, ф-ла (12.20)].
Решим полученную систему уравнений (10)относительно функций ![]() и
и ![]() .
.
Предварительно запишем уравнения (10) в виде системы уравнений
 (11)
(11)
где ![]()
![]()
![]()
![]()
где ![]()
![]()
Определитель системы уравнений (11) имеет вид
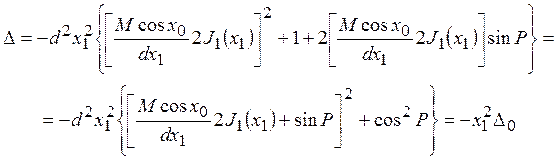 (12)
(12)
Отсюда при условиях (9) приходим к [7, ф-ле (12.23)] с точностью до коэффициента(![]() )
)
В результате находим
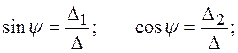
где 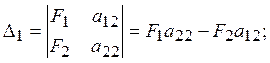

После преобразований Δ1 и Δ2 принимает вид


Таким образом, находим искомые решения системы уравнений (11)
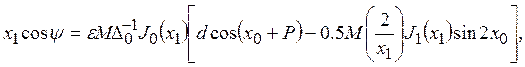
(13)
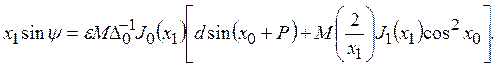
где Δ0=-Δ/x12
Отсюда при условиях (9) приходим к [7, ф-ла (12.21)].
По (13) находим выражения для квадрата амплитуды первой гармоники (x12).
![]() (14)
(14)
Отсюда при условиях (9) приходим к [7, ф-ла (12.22)].
Раскрывая в (14) значение величины Δ0, получим
 (15)
(15)
или при выполненных условиях (9)
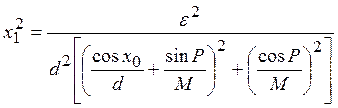 (16)
(16)
Отсюда следует [4]

где δ=d/M.
В [4] показано, что это значение x1 при ![]() можно аппроксимировать величиной
можно аппроксимировать величиной
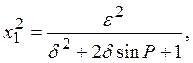 (17)
(17)
В случае системы первого порядка, когда P=0, M=1, полагая ![]() , получим
, получим

Таким образом, формула (17) здесь справедлива при β=0 и в том случае, если выполнено условие (9)
Кривые ![]() при ε=const, приведены на рис. 1. Кривые 1,4 – получены при ε=0.9;2,5 при ε=0.6; 3,6 при ε=0.3. При d>>1 получим асимптотическую формулу
при ε=const, приведены на рис. 1. Кривые 1,4 – получены при ε=0.9;2,5 при ε=0.6; 3,6 при ε=0.3. При d>>1 получим асимптотическую формулу ![]() (на рис. 1 штриховые линии)
(на рис. 1 штриховые линии)
Нетрудно убедиться, что формула (17) здесь справедлива при любом фильтре (при P≠0; M≠1), если положить ![]() и взять β=0.
и взять β=0.
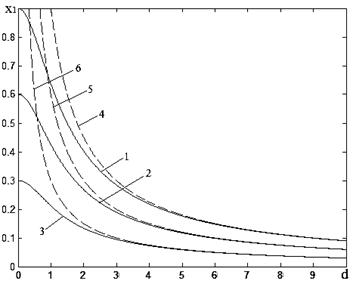
Рисунок 1
При использовании в качестве фильтра низкой частоты (ФНЧ) интегрирующей цепи, имеем
![]()
где ![]()
![]() - постоянная времени ФНЧ.
- постоянная времени ФНЧ.
В таком случае по (17) находим ![]() ,
,

При d>>1, α<<1 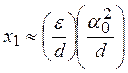 Следовательно, при этом графики зависимости x1=f(d) располагаются ниже кривых системы первого порядка. Заметим, что полоса захвата ФАП при отсутствии помехи при малых α0 имеет вид βk=(4/π)α0
Следовательно, при этом графики зависимости x1=f(d) располагаются ниже кривых системы первого порядка. Заметим, что полоса захвата ФАП при отсутствии помехи при малых α0 имеет вид βk=(4/π)α0
Для дальнейших исследований необходимо найти выражения для функции sinP и cosP.
По (13) получим

Полагая cosx0=a; sinx0=b; cosP=x; sinP=y, решим систему уравнений
![]()
В результате получим
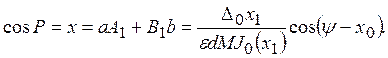 (18)
(18)
 (19)
(19)
Подставим значения cosP и sinPв формулу для Δ0. В результате находим:
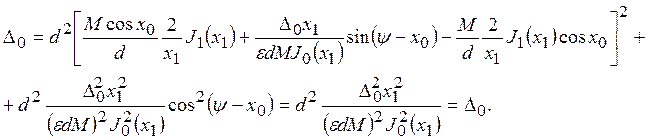
Тогда
 (20)
(20)
Подставляя это значение Δ0 в (18) и (19), окончательно приходим к соотношениям
![]()
![]() (21)
(21)
Найдем значение sinx0, используя (8) и выражая сos(x0-ψ) из (20). В результате получим
 (22)
(22)
Отсюда при условиях (9) приходим к [7, ф-ла (12.24)]
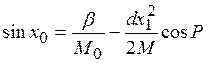 (23)
(23)
На рис. 2а изображены зависимости ![]() при ε=0.6, a=0.8 и
при ε=0.6, a=0.8 и ![]() , где кривые 1,4 получены при β=0.8; 2,5 – β=0.5; 3,6 – β=0.2; Кривые 1, 2, 3 – при невырожденном фильтре, 4, 5, 6 – при вырожденном. На рис. 2б изображены зависимости
, где кривые 1,4 получены при β=0.8; 2,5 – β=0.5; 3,6 – β=0.2; Кривые 1, 2, 3 – при невырожденном фильтре, 4, 5, 6 – при вырожденном. На рис. 2б изображены зависимости ![]() при β=0.5, a=0.8 и
при β=0.5, a=0.8 и ![]() , где кривые 1,2 получены при ε=0.9; 3,4 – ε=0.6; 5,6 – ε=0.3; Кривые 1, 3, 5 – при невырожденном фильтре, 2, 4, 6 – при вырожденном. На рис. 3aизображены зависимости
, где кривые 1,2 получены при ε=0.9; 3,4 – ε=0.6; 5,6 – ε=0.3; Кривые 1, 3, 5 – при невырожденном фильтре, 2, 4, 6 – при вырожденном. На рис. 3aизображены зависимости ![]() при ε=0.6, a=0.8 и
при ε=0.6, a=0.8 и ![]() , где кривые 1,2 получены при β=0.8; 3,4 – β=0.5; 5,6 – β=0.2. На рис. 3б изображены зависимости
, где кривые 1,2 получены при β=0.8; 3,4 – β=0.5; 5,6 – β=0.2. На рис. 3б изображены зависимости ![]() при β=0.5, a=0.8 и
при β=0.5, a=0.8 и ![]() , где кривые 1,2 получены при ε=0.9; 3,4 – ε=0.6; 5,6 – ε=0.3. На рисунках 3а,б кривые 1, 3, 5 получены при невырожденном фильтре, 2, 4, 6 – при вырожденном.
, где кривые 1,2 получены при ε=0.9; 3,4 – ε=0.6; 5,6 – ε=0.3. На рисунках 3а,б кривые 1, 3, 5 получены при невырожденном фильтре, 2, 4, 6 – при вырожденном.
По (21) находим
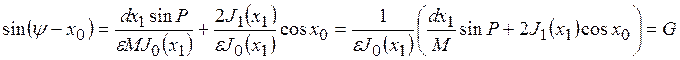 (24)
(24)
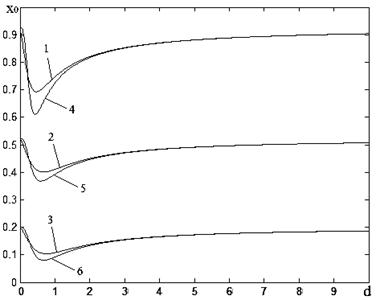
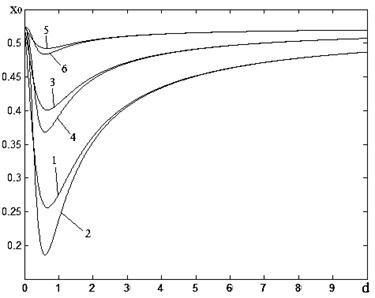
Рисунок 2а Рисунок 2б
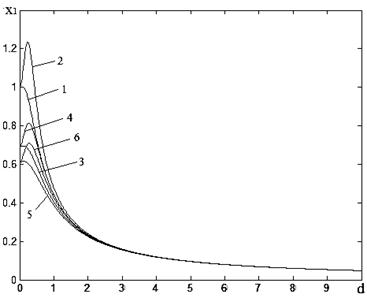
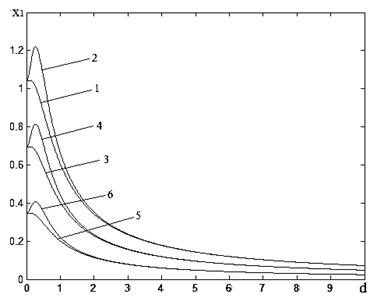
Рисунок 3а Рисунок 3б
Тогда
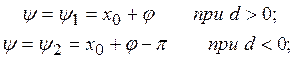 (25)
(25)
где φ=arcsinG
Действительно, ![]() причем плюс при d>0, минус при d<0, так как cosP>0 и
причем плюс при d>0, минус при d<0, так как cosP>0 и ![]()
Зависимости ![]() изображены на рис. 4, при ε=0.6 a=0.8 и
изображены на рис. 4, при ε=0.6 a=0.8 и ![]() , где кривые 1, 3, 5 получены при невырожденном фильтре; 2, 4, 6 – при вырожденном. Кривые 1, 2 получены при β=0.8; 3, 4 - β=0.5; 5, 6 - β=0.2.
, где кривые 1, 3, 5 получены при невырожденном фильтре; 2, 4, 6 – при вырожденном. Кривые 1, 2 получены при β=0.8; 3, 4 - β=0.5; 5, 6 - β=0.2.
Поэтому по (20) находим
![]()
Отсюда получим
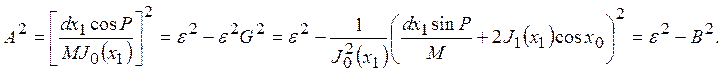
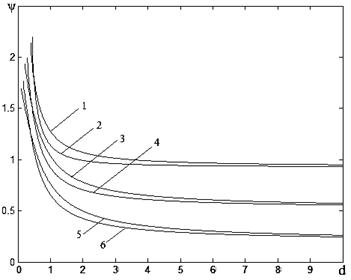
Рисунок 4
Тогда
![]() (26)
(26)
Тогда используя равенство (20), по (13) находим
![]()
![]() (27)
(27)
где 
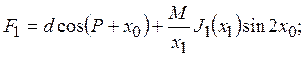
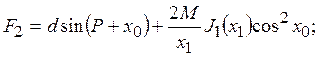
Найдем приближенные значения параметров колебаний x0, x1, ψ
По (16) при d>>1 следует
 (28)
(28)
Отсюда при J0(x1)=1 получим [7, ф-ле (12.25)]
Поскольку x1J1(x1) ~ x12 ~ 1/d2, то по (21) находим приближенную формулу
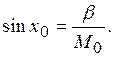 (29)
(29)
При малых x1 (при больших помеховых расстройках d>>1), когда J1(x1) ≈ x1/2 по (24) получим 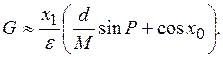 Отсюда при d>>1 с учетом значения x1 по (27) находим G≈sinP и φ=P; ψ1≈x0+P [7, ф-ла (12.27)].
Отсюда при d>>1 с учетом значения x1 по (27) находим G≈sinP и φ=P; ψ1≈x0+P [7, ф-ла (12.27)].
Таким образом, получены соотношения для всех трех параметров x0, x1, ψ, предполагаемого решения.
2. Критические значения параметров
Найдем критические значения первой гармоники x1=x1k и отношения помеха/сигнал ε=εk, которые определяют условия срыва синхронизации:
![]() (30)
(30)
При учете второго условия по (16) находим ![]() . Отсюда следует
. Отсюда следует
![]() (31)
(31)
При учете первого равенства в (29) находим
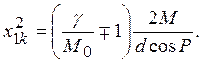 (32)
(32)
Подставляя это значение ![]() в (30) окончательно получим
в (30) окончательно получим
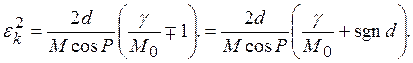 (33)
(33)
Зависимость ![]() при a=0.8 и
при a=0.8 и ![]() изображена на рис. 5, где кривая 1 получена при ФАП 1-го порядка и β=0; кривая 2 при невырожденном и вырожденном фильтре и β=0; 3 – ФАП 1-го порядка β=0.8; 4 - невырожденный и вырожденный фильтр и β=0.8;
изображена на рис. 5, где кривая 1 получена при ФАП 1-го порядка и β=0; кривая 2 при невырожденном и вырожденном фильтре и β=0; 3 – ФАП 1-го порядка β=0.8; 4 - невырожденный и вырожденный фильтр и β=0.8;
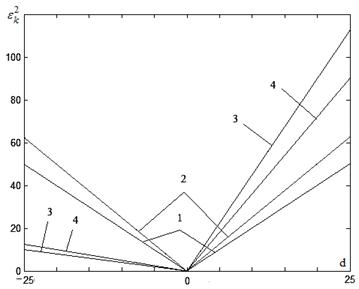
Рисунок 5
По рис. 5 замечаем что при β>0 и d>0 помехоустойчивость ФАП выше, чем β>0, а d<0.
Можно показать, что условиями захвата за сигнал при действии гармонической помехи является [5]
![]()
или
![]()
С другой стороны по [9] находим
![]()
или
![]()
Причем во втором случае границы захвата по сигналу совпадают с [8] несмотря на то что получены [5,8] и [9] на основе разных критериев.
Достаточным условием захвата за помеху является условие [5]

или
![]()
Причем левая граница во втором случае совпадает с [8].
Заключение
Таким образом, в более строгом приближении, чем в [7] получены динамические характеристики фазовой автоподстройки при наличии на ее входе гармонической помехи. Найдены зависимости параметров предполагаемого решения ДУ от параметров помехи и сигнала. Приведены соотношения для критических значений этих параметров.
Приложение
Амплитудночастотные и фазочастотные характеристики (АЧХ и ФЧХ) фильтров низкой частоты (ФНЧ) ФАП.
Пропорционально интегрирующий фильтр (ПИФ)
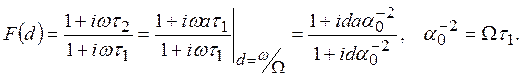
АЧХ 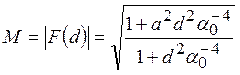
ФЧХ ![]()
Вырожденный ПИФ
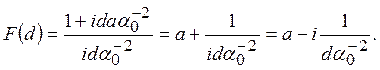
АЧХ 
ФЧХ 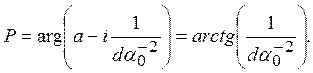
Данные характеристики используются при построении рисунков в статье.
Литература
1. Журавлев А.Г. Работа системы фазовой автоподстройки частоты при гармонических помехах// Радиотехника. 1963. т. 18, №9, С. 38-46.
2. Bruno F. Tracking performance and loss of lock of a carrier loop due to the presence of a spoofed spread spectrum signal // Proceedings of the 1973 symposium on spread spectrum communications, v.1 San Diego, California, 1973, March, pp 71-75
3. Blanchard A. Interference in phase – locked loops // IEEE Trans. On aerospace and electronic systems, 1974, v. AE S-10, N 5, p. 686-697
4. Levitt B.K. Carrier tracking loop performance in the presence of a strong CW interference// IEEE Trans. on communications, 1981, v. COM -29, N6, p 911-916
5. Nakagawa M. Effects of interfering signals in phase-locked loops // Frequentz, 1978, v. 32, №5, P. 146-153.
6. Быховский М.А. Влияние помехи на процессы захвата в системе фазовой автоподстройки частоты // Радиотехника и электроника. 1987. №10 С. 2131-2141
7. Шахтарин Б.И. Статистическая динамика систем синхронизации. М.: Радио и связь, 1998. – 488 с.
8. Шахтарин Б.И. Анализ систем синхронизации методом усреднения. – М.: Радио и связь, 1999.-496с.
9. Karsi M.F., Lindsey W.C. Effects of CW interference on phase-locked performance // IEEE Trans., 2000, v. COM-48, № 5, p. 886-896
10. Шахтарин Б.И., Иванов А.А., Кобылкина П.И. и др. Синхронизация в радиосвязи и радионавигации. – М.: Гелиос АРВ, 2007. – 256 с.
11. Шахтарин Б.И., Асланов Т.Г. Сравнительный анализ характеристик воздействия помех на системы синхронизации // Телекоммуникационные системы и технологии: 4-ый Межд. радиоэлек. форум. Украина, Харьков, 2011 С. 187-190.
12. Шахтарин Б.И., Асланов Т.Г. Анализ систем синхронизации численными методами // Вестник МГТУ им. Н.Э. Баумана. Сер. Приборостроение 2011. - №4
Публикации с ключевыми словами: помехоустойчивость, помеха, фазовая автоподстройка, метод гармонического баланса
Публикации со словами: помехоустойчивость, помеха, фазовая автоподстройка, метод гармонического баланса
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



