научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2011
УДК 004.436.4
МГТУ им. Н.Э. Баумана
![]() Система отличается многочисленными характеристиками, определяемыми аспектами ее описания. Нас будет интересовать сейчас и в дальнейшем анализ процесса ее функционирования. Под функционированием системы понимается процесс изменения ее состояния во времени. В статье рассматривается способ описания такого процесса с учетом того, что система имеет высокую размерность, разделяется на множество объектов, различным способом связанных между собой, руководствуется сложными алгоритмами, описывающими переход из одного состояния в другое.
Система отличается многочисленными характеристиками, определяемыми аспектами ее описания. Нас будет интересовать сейчас и в дальнейшем анализ процесса ее функционирования. Под функционированием системы понимается процесс изменения ее состояния во времени. В статье рассматривается способ описания такого процесса с учетом того, что система имеет высокую размерность, разделяется на множество объектов, различным способом связанных между собой, руководствуется сложными алгоритмами, описывающими переход из одного состояния в другое.
Всю совокупность параметров системы, определяющих процесс функционирования или участвующих в нем, назовем параметрическим множеством системы ![]() , где qi – некоторый параметр. Каждый параметр qi принимает множество значений, обозначаемое в дальнейшем как σ(qi).
, где qi – некоторый параметр. Каждый параметр qi принимает множество значений, обозначаемое в дальнейшем как σ(qi).
Определим пространство состояний системы как Декартово произведение S=![]() σ(qi). В этом пространстве каждый параметр выступает в роли координаты, а размерность пространства равна мощности множества Q. Элемент пространства S есть возможное состояние системы.
σ(qi). В этом пространстве каждый параметр выступает в роли координаты, а размерность пространства равна мощности множества Q. Элемент пространства S есть возможное состояние системы.
В дальнейшем нас будет интересовать процесс изменения состояний системы во времени. Примем за основу определение процесса, предложенное в работе [1].
Процесс Z есть четверка:
Z=< S, T, F, α > | (1) |
где:
S - пространство состояний системы, определенное ранее;
T - множество моментов времени изменения состояний системы;
F – график процесса, определяемый как отображение T→S, причем это отображение должно быть функциональным (однозначным);
α- отношение линейного порядка на T.
Если множество T задано как упорядоченное, то в определении процесса α может быть опущено.
В общем случае множества T и S могут быть как дискретными, так и непрерывными.
Интервал времени [tН, tК], где tН=min{T}, tК=max{T}, назовем интервалом определения процесса.
Поскольку пространство S координатного типа, то в случае необходимости подчеркнуть систему координат Q, на которой оно определено, будем обозначать его также SQ.
В этих обозначениях, если множество Т задано, как упорядоченное, а пространство S определено на множестве параметров Q, определить процесс можно как: Z=< SQ, T, F >.
Кортеж ![]() , где
, где ![]() - значения элементов множества X , будем обозначать как
- значения элементов множества X , будем обозначать как ![]() .
.
Определим фазовое пространство Ф процесса Z как Ф=T´S .
Тогда график F есть подмножество Ф.
Если f∈ F, то f = <t, ![]() >, где t∈T.
>, где t∈T.
Если Q1![]() Q, то определим понятие проекции f на пространство
Q, то определим понятие проекции f на пространство ![]() как:
как:
![]() = <t,
= <t,  >. Проекцией f на T является t.
>. Проекцией f на T является t.
Пусть процесс Z задан на интервале [tН, tК]. Введем понятие подпроцесса Z i как плотное во времени подмножество процесса Z на интервале [ti; tj] при условии, что [ti; tj] ![]() [tН, tК]. Плотность по времени означает, что на интервале [ti; tj] нет ни одной точки, принадлежащей Т и не относящейся к подпроцессу Z i. Этот интервал назовем интервалом определения подпроцесса. Понятие подпроцесса позволяет рассматривать процесс в виде последовательности подпроцессов и производить операции разделения и объединения фрагментов процесса.
[tН, tК]. Плотность по времени означает, что на интервале [ti; tj] нет ни одной точки, принадлежащей Т и не относящейся к подпроцессу Z i. Этот интервал назовем интервалом определения подпроцесса. Понятие подпроцесса позволяет рассматривать процесс в виде последовательности подпроцессов и производить операции разделения и объединения фрагментов процесса.
Рассмотрим ряд операций над процессами, описываемых с помощью введенных выше понятий.
Операция свертки процесса
Пусть задан процесс Z=<S, T, F, α>
Процесс Z1=<S1, T1, F1, α1> является сверткой процесса Z, если он получен в результате следующих преобразований:
а) произведено полное разбиение интервала определения процесса Z на n непересекающихся подинтервалов [τj, τj+1], где j=1..n, причем τ1=tН , τn+1=tК . В результате получим разбиение процесса Z на n подпроцессов Z j (j=1..n);
б) поставим в соответствие каждому подпроцессу Zj одно значение состояния ![]() из множества S1 и одно значение времени βj из интервала [τj, τj+1]. В результате получим дискретное множество
из множества S1 и одно значение времени βj из интервала [τj, τj+1]. В результате получим дискретное множество ![]() , график
, график ![]() , отношение α1
, отношение α1![]() α.
α.
Таким образом, получим новый процесс Z1, который и называется сверткой процесса Z. Очевидно, процесс Z1 дискретен во времени. Никаких ограничений на характер пространства состояний S1 не накладывается. Однако на практике при проведении операции свертки пространство S1, как правило, оказывается значительно меньшей мощности, чем исходное пространство S.
Рассмотрим для примера процесс решения задачи c использованием CPU и жесткого диска HD (рис. 1).

Рисунок 1. Пример операции свертки процесса
Пусть исходный процесс Z описан в пространстве S, имеющем следующие состояния: {обращение к памяти, загрузка регистров, операции сумматора, головка диска, запись-считывание на диске, печать результата}. Множество моментов времени изменения состояния Т={0, t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11}.
Допустим, что нам необходимо построить процесс Z1, отражающий лишь длительность занятия задачей CPU и жесткого диска HD. Для этого зададим новое пространство S1, имеющее следующие состояния: {ожидание, решение в CPU, работа с HD}. Разобьем интервал определения процесса Z на подинтервалы: П1, П2, П3, П4, П5. Это разбиение определяет также соответствующие подпроцессы процесса Z. Выполним отображение подпроцессов процесса Z на фазовую плоскость процесса Z1: П1 отображается в точку А, П2 – в точку В, П3 – в точку С, П4 – в точку D, П5 – в точку Е. В результате получим процесс Z1 с пространством состояний S1, множеством моментов времени изменения состояния Т1={0, t1, t7, t8, t10}. График этого процесса приведен на этом же рисунке.
Как видно из примера, операция свертки порождает новый процесс, дискретный во времени, поскольку подпроцессы процесса Z, имеющие конечную длительность, отображаются лишь на одну точку фазовой плоскости нового процесса Z1.
Операция свертки относится к классу операций анализа.
Операция развертки
Операция развертки обратна по отношению к операции свертки: процесс Z является разверткой процесса Z1. При выполнении этой операции необходимо каждую точку ![]() процесса Z1 развернуть в подпроцесс Z j.
процесса Z1 развернуть в подпроцесс Z j.
Операция развертки относится к классу операций синтеза.
Операция проецирования
Процесс Z1 является проекцией процесса Z на координатное пространство ![]() (обозначение
(обозначение ![]() ), если Q1
), если Q1![]() Q и процесс построен по следующей процедуре:
Q и процесс построен по следующей процедуре:
1) каждую точку графика F проецируем на пространство ![]() . В результате получаем множество
. В результате получаем множество ![]() . Мощность множества
. Мощность множества ![]() равна мощности множества F ;
равна мощности множества F ;
2) упорядочиваем множество ![]() в соответствие с α. Результат действий 1) и 2) будем называть отображением процесса Z на пространство
в соответствие с α. Результат действий 1) и 2) будем называть отображением процесса Z на пространство ![]() ;
;
3) вводим отношение эквивалентности на множестве ![]() такое, что r подряд расположенных точек fi+1 ,… fi+r множества
такое, что r подряд расположенных точек fi+1 ,… fi+r множества ![]() ( fi+1= <ti+1, s1i+1> ,… fi+r=<ti+r, s1i+r>) считаются эквивалентными, если s1i+1= s1i+2 = …=s1i+r
( fi+1= <ti+1, s1i+1> ,… fi+r=<ti+r, s1i+r>) считаются эквивалентными, если s1i+1= s1i+2 = …=s1i+r
r может принимать любые положительные целые значения, начиная от 1. Таким образом формируются классы эквивалентных значений KЭ . При r=1 класс содержит одну единственную точку.
4) каждому классу эквивалентности KЭ на ![]() ставим в соответствие одну точку fэкв= <tmin, sэкв> где
ставим в соответствие одну точку fэкв= <tmin, sэкв> где ![]() , sэкв=s1i=… для всего класса КЭ
, sэкв=s1i=… для всего класса КЭ
5) формируем множество F1 из элементов fэкв по всем классам эквивалентности на ![]() , мощность F1 равна количеству классов эквивалентности на
, мощность F1 равна количеству классов эквивалентности на ![]() .
.
6) проецируя F1 на T, получим множество T1. Очевидно, что T1![]() T, сужение отношения α на T1 обозначим α1.
T, сужение отношения α на T1 обозначим α1.
В результате выполнения вышеуказанных операций получим процесс ![]() :
:
Z1=<![]() , T1, F1, α1>.
, T1, F1, α1>.
Пользуясь операцией проецирования, можно переопределить понятие подпроцесса:
![]()
Пример операции проецирования приведен на рис. 2. На нем показан исходный процесс Z, заданный в двухпараметрическом пространстве S=σ(А)хσ(В), где σ(А)={g, h, k, m, n}, σ(B)={a, b, c, d}. Ось времени не показана, однако значения моментов времени изменения состояний указаны в кружочках, обозначающих соответствующее состояние. Таким образом, как видно из рисунка, множество Т={1, 2, 3, 4, 5, 6, 7, 8, 9}.

Рисунок 2. Процесс Z в двухпараметрическом пространстве
График процесса F={<1,<g,a>, <2,<h,c,>, <3,<h,b>, <4,<k,a>, <5,<m,a>, <6,<m,d>, <7,<n,d>, <8,<n,b>, <9,<k,b>}
Построим процесс ![]() , являющийся проекцией процесса Z на пространство s(А), в соответствие с алгоритмом выполнения операции проецирования.
, являющийся проекцией процесса Z на пространство s(А), в соответствие с алгоритмом выполнения операции проецирования.
1) Строим график ![]() А={<1,g>, <2,h>, <3,h>, <4,k>, <5,m>, <6,m>, <7,n>, <8,n>, <9,k>}
А={<1,g>, <2,h>, <3,h>, <4,k>, <5,m>, <6,m>, <7,n>, <8,n>, <9,k>}
2) Множество ![]() А уже упорядочено по времени. Получаем отображение процесса Z на пространство s(А), показанное на рис. 3.
А уже упорядочено по времени. Получаем отображение процесса Z на пространство s(А), показанное на рис. 3.
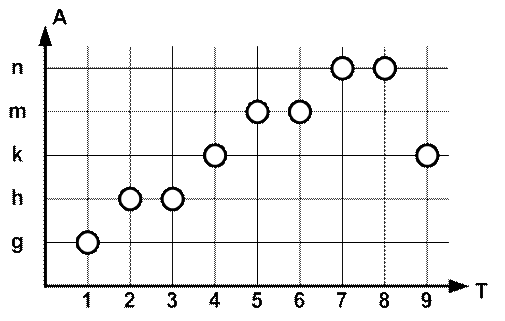
Рисунок 3. Отображение процесса Z на параметр А
3) На множестве ![]() А определяем классы эквивалентности: К1 – точка 1, К2 – точки 2,3, К3 – точка 4, К4 – точки 5,6, К5 – точки 7,8, К6 – точка 9.
А определяем классы эквивалентности: К1 – точка 1, К2 – точки 2,3, К3 – точка 4, К4 – точки 5,6, К5 – точки 7,8, К6 – точка 9.
4) Ставим в соответствие классу К2 точку <2,h>, классу К4 точку <5,m>, классу К5 точку <7,n>.
5) Формируем график FA={<1,g>, <2,h>, <4,k>, <5,m>, <7,n>, <9,k>}
6) Формируем множество времен изменения состояний ТА=<1,2,4,5,7,9>
Полученный в результате проведенных операций процесс ![]() показан на рис. 4.
показан на рис. 4.
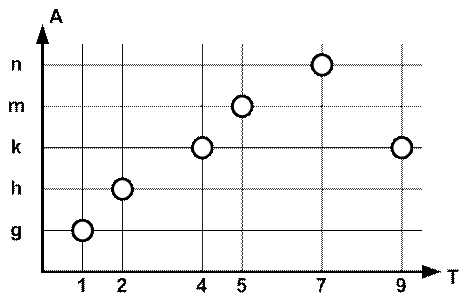
Рисунок 4. Процесс ZA – проекция процесса Z на параметр А
Аналогично строится и проекция процесса Z на параметр В (пространство, состоящее из единственного параметра). Процесс ZB показан на рис. 5.
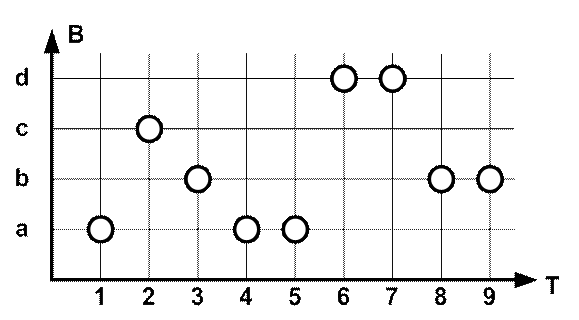
Рисунок 5. Отображение процесса Z на параметр В
После выполнения пункта 5. алгоритма получим результат, представленный на рис. 6.

Рисунок 6. Процесс ZВ - проекция процесса Z на параметр В
Операция объединения
Пространство SQ называется склейкой пространств ![]() и
и ![]() , если Q=Q1
, если Q=Q1![]() Q2. Интерес представляет случай непустого пересечения Q1 и Q2., когда пространства
Q2. Интерес представляет случай непустого пересечения Q1 и Q2., когда пространства ![]() и
и ![]() имеют общую область.
имеют общую область.
Пусть кортеж s1 принадлежит пространству ![]() , кортеж s2 принадлежит пространству
, кортеж s2 принадлежит пространству ![]() .Обозначим значения параметра q из кортежа s1 как
.Обозначим значения параметра q из кортежа s1 как ![]() , а значение параметра q из кортежа s2 как
, а значение параметра q из кортежа s2 как ![]() .
.
Тогда s1=<…![]() …>, s2=<…
…>, s2=<…![]() …>.
…>.
Кортеж s является левой склейкой кортежей s1 и s2, когда:
sл= <…![]() …
…![]() …>.
…>.
Правая склейка определяется как:
sп= <…![]() …
…![]() …>.
…>.
Если sл=sп, то склейка называется функциональной.
Пусть заданы процессы Z1=<![]() , T1, F1, α1> и Z2=<
, T1, F1, α1> и Z2=<![]() , T2, F2, α2>. Процесс Z=<
, T2, F2, α2>. Процесс Z=<![]() , T, F, α> является объединением процессов Z1 и Z2 (обозначение Z= Z1
, T, F, α> является объединением процессов Z1 и Z2 (обозначение Z= Z1![]() Z2), если:
Z2), если:
· SQ является склейкой пространств ![]() и
и ![]()
· T= T1![]() T2
T2
· для каждого t∈T строится: ft=<t, st>, где st – склейка кортежей s1t (s1t∈![]()
![]() ) и s2t (s2t∈
) и s2t (s2t∈![]() ) , кортежи s1t и s2t принадлежат соответственно графикам F1 и F2 для значения t
) , кортежи s1t и s2t принадлежат соответственно графикам F1 и F2 для значения t
· все склейки кортежей s1t и s2t для всех t∈T являются функциональными
· совокупность ft для всех t∈T формирует график F
· отношение α строится как транзитивное замыкание на α1![]() α2.
α2.
Процессы Z1 и Z2 , допускающие операцию объединения, называются согласованными.
Можно доказать ряд утверждений
Утверждение 1.
Два процесса Z1 с пространством состояний ![]() и Z2 с пространством состояний
и Z2 с пространством состояний ![]() согласованы, если Q1
согласованы, если Q1![]() Q2=Ø.
Q2=Ø.
Утверждение 2.
Пусть задан процесс Z1 с пространством состояний ![]() и Z2 с пространством состояний
и Z2 с пространством состояний ![]() . Пусть в некоторой момент времени t состояние Z1 равно s1∈
. Пусть в некоторой момент времени t состояние Z1 равно s1∈![]() , а состояние Z2 равно s2∈
, а состояние Z2 равно s2∈![]() . В общем случае будем полагать, что Q1
. В общем случае будем полагать, что Q1![]() Q2≠Ø. Обозначим Q3=Q1
Q2≠Ø. Обозначим Q3=Q1![]() Q2.
Q2.
Если для всех моментов времени t∈T значения <…![]() …>=<…
…>=<…![]() …>, то процессы Z1 и Z2 –согласованы.
…>, то процессы Z1 и Z2 –согласованы.
Утверждение 3.
Если ![]() и
и ![]() , то процессы Z1 и Z2 согласованы.
, то процессы Z1 и Z2 согласованы.
Утверждение 4.
Пусть заданы процесс Z1, определенный на интервале ![]() , и Z2, определенный на интервале
, и Z2, определенный на интервале ![]() .
.
Если ![]()
![]()
![]() =Ø, то процессы Z1 и Z2 согласованы.
=Ø, то процессы Z1 и Z2 согласованы.
Сформулированные выше утверждения позволяют выработать практически важные рекомендации по управлению процессами с тем, чтобы осуществить их объединение.
Литература
1. Бусленко Н.П., Калашников В.В., Коваленко И.Н. Лекции по теории сложных систем. - М.: Сов.Радио, 1973. - 438 с.
2. Черненький В.М. Процессно - ориентированная концепция системного моделирования АСУ: Дис...док. тех. наук.-М.,2000.-350с.
Публикации с ключевыми словами: процесс, пространство состояний, функционирование системы, параметры системы, операции над процессами, объединение процессов
Публикации со словами: процесс, пространство состояний, функционирование системы, параметры системы, операции над процессами, объединение процессов
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



