научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2011
УДК 621.436
МГТУ им. Н.Э. Баумана
При моделировании рабочего цикла дизеля существует необходимость в определении температур деталей камеры сгорания. Это необходимо как для определения теплообмена в цилиндре двигателя, так и для моделирования смесеобразования и сгорания [1]. Для определения теплового состояния деталей камеры сгорания двигателя, необходимо решить задачу теплопроводности. Для решения этой задачи применительно к двигателям используют граничные условия третьего рода.
Для расчета параметров теплообмена со стороны подвода тепла из камеры сгорания существует большое количество экспериментальных формул [7]. Причем наиболее хорошо зарекомендовала себя формула Вошни, и расчет осредненных параметров теплообмена по цилиндру по этой формуле дает хорошее совпадение с экспериментом. Для расчета параметров теплообмена со стороны теплоотвода также существует большое количество формул и рекомендаций, однако существует ряд проблемных зон, где эмпирические или полуэмпирические формулы дают результаты, различающиеся на порядок. В частности сложности проявляются при расчете параметров теплообмена в зазоре между кольцом и втулкой цилиндра. В настоящее время для определения параметров теплообмена в этой области используют решение уравнения Рейнольдса в различных формах записи.
Согласно данным различных авторов [2, 3] через сопряжение кольцо-втулка от поршня отводится от 30 до 60 % тепла. При этом 40 … 60 % хода поршня кольцо находится в режиме гидродинамического трения. Поэтому необходимо иметь адекватную модель расчета режима гидродинамического трения трибосопряжения кольцо-втулка. Расчет коэффициента теплоотдачи на режиме гидродинамического трения можно найти в работах [2, 3, 5]. Согласно этим моделям для определения коэффициента теплоотдачи необходимо знать толщину масляного слоя под кольцом. Для расчета толщины масляного слоя предложены различные методы [2, 3, 5], однако описание алгоритма расчета носит либо формальный характер, либо предложенная модель проявляет неустойчивость при численном решении и необходимо существенно уменьшать шаг по времени. Поэтому была проведена работа по поиску способа расчета, который давал бы устойчивое решение при любых возможных вариантах геометрии кольца и условиях работы двигателя. Результаты данной работы отражены в данной статье.
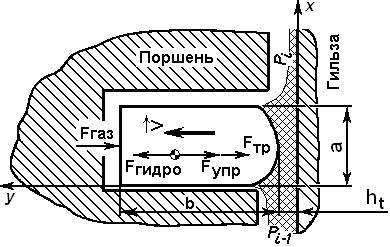
Расчетная схема динамики кольца [2], с указанием сил, действующих на кольцо, приведена на рисунке 1. Для решения задачи динамики движения кольца в радиальном направлении воспользуемся уравнением 2-го закона Ньютона:
![]() , (1)
, (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
где mк – масса кольца;
h – толщина масляного слоя под данной точкой кольца;
hx – профиль кольца, зависит только от координаты x (см. рис. 1);
ht – расстояние от минимальной точки кольца до гильзы (см. рис. 1);
V – скорость кольца в радиальном направлении;
Fгидро – сила от действия гидродинамического давления масла;
Fгаз – сила от давления газа за кольцом;
Fупр – сила упругости кольца;
Fтр – сила трения кольца о канавку поршня.
|
Рис. 1. Схема сил, действующих на кольцо. |
Решением дифференциального уравнения (ДУ) (1), является толщина масла под кольцом - ht. Суммарная толщина масляного слоя h, делится на толщину масляного слоя, соответствующего профилю кольца hx, а также на толщину слоя масла, зависящего только от времени, и характеризующего радиальную скорость перемещения кольца – ht.
Расчет силы от давления газа за кольцом производится согласно выражению [5]:
![]() ,
,
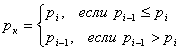 .
.
Сила упругости кольца задается в явном виде, причем среднее давление кольца на поверхность цилиндра, вычисляемое по выражению ![]() , для большого числа двигателей составляет от 0,1 до 0,4 МПа.
, для большого числа двигателей составляет от 0,1 до 0,4 МПа.
Принимая во внимание оценку скорости перемещения кольца в радиальном направлении [5], а так же размеры кольца можно предположить, что режим трения кольца о кольцевую канавку носит скорее характер сухого трения. При этом, в связи с обильным количеством смазки, находящимся на данных поверхностях, коэффициент трения будет иметь значение ниже 0,1. Учитывая размеры кольца a и b можно сделать заключение, что сила трения в этой зоне будет на порядок меньше силы прижатия кольца к цилиндру. Поэтому в дальнейших расчетах будем пренебрегать этой силой.
Для определения силы, поднимающей кольцо над поверхностью цилиндра, необходимо найти распределение давления в масляном слое. Для расчета гидродинамического режима трения кольца по втулке воспользуемся системой уравнений для плоской задачи гидродинамики смазки, приведенной в [6]. Возможность применения плоской задачи для слоя масла в кольцевом зазоре двигателя обосновывается в книге [5], и в настоящее время является обычной практикой при расчете гидродинамики колец и поршней.
![]() , (4)
, (4)
где p – давление под кольцом, [Па];
μ – коэффициент динамической вязкости, [Па·сек];
U – скорость движения кольца, [м/сек].
Существует как аналитическое, так и численное решение ДУ (4). Однако, как показала практика применения обоих методов, для использования решения при вычислениях на компьютере, для колец с произвольным профилем, предпочтительнее полностью численный алгоритм, так как он поддается более простой алгоритмизации и приводит к более быстрому маршевому счету.
Численный метод для решения ДУ (4) был взят из работы [10]. Расчетная схема приведена на рисунке 2.
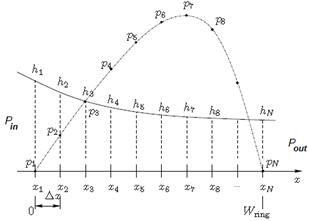
Рис. 2. Расчетная схема для решения ДУ (4).
Для определения распределения давления в слое смазки в работе [10] решалось ДУ
![]() . (5)
. (5)
Конечно-разностный аналог ДУ (5)
![]() .
.
Для узлов i=2, 3, … , N-1, где N – число узлов профиля кольца, конечно-разностный аналог ДУ (5), в матричной форме записывается следующим образом
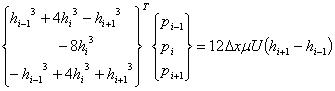 .
.
Для граничных узлов i=1 и N, задается давление явно pin, pout соответственно (см. рис. 2). Общий вид решаемой системы линейных алгебраических уравнений (СЛАУ) представляет собой прямоугольную матрицу коэффициентов трехдиагонального вида
![]() , (6)
, (6)
где 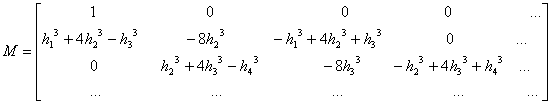
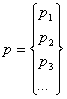
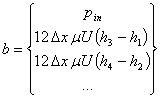
В качестве эксперимента, для получения большей точности расчета, для ДУ (1), при расчете распределения давления в слое смазки использовалось ДУ (4). В этом случае правая часть СЛАУ (6) примет вид
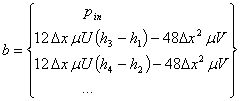
В связи с тем, что при движении кольца (см. рис. 3) возникает зона отрицательного давления – кавитационная область, необходимо, при нахождении равнодействующей силы гидродинамического давления исключать зону пониженных давлений при интегрировании. В работе [10] рассмотрены методы решения проблемы устранения зоны кавитации в расчете. Однако, все они требуют как минимум двойного пересчета профиля давления, а значит скорость решения задачи динамики кольца упадет минимум в 2 раза. При этом точность расчета профиля давления увеличивается не более чем на 20 %.
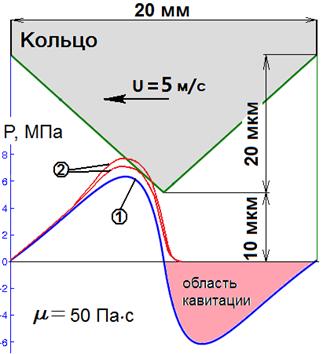
Рис. 3. Расчет профиля давления под кольцом с симметричным профилем.
(1) – профиль давления в слое масла, при решении ДУ (4) по всей ширине кольца; (2) – профили давления масла под кольцом при использовании итерационных методов решения ДУ (4) из работы [10]
Для решения задачи гидродинамики кольца дизеля это не большая ошибка, так как в данной модели не учитывается сложное движения кольца относительно гильзы цилиндра, когда существенное влияние оказывает профиль канавки кольца, вторичная динамика поршня, скручивание кольца и т.д. [11].
Для решения ДУ (1) динамики кольца был использован численный метод Рунге-Кутта, для дифференциальных уравнений второго порядка [8]. Перепишем уравнение (1) в виде, удобном для записи общего алгоритма решения ДУ:
![]()
Формулы для решения ДУ имеют следующий вид:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Анализ устойчивости производился с помощью численных экспериментов, варьированием шага по времени. Расчет давления в смазочном слое находилось решением ДУ (5). Кольцо имело профиль, указанный на рис. 4, шаг узлов в профиле кольца (Δx) составлял 0,1 мм.
Точность метода проверялась сравнением результатов, полученных расчетом и на экспериментальной установке, описанной в работе [9].
При решении расчете давления под кольцом по ДУ (4) минимально необходимый шаг составлял 4×10-5 градуса по углу поворота коленчатого вала, время счета на компьютере Intel Core 2 Duo, 2,2 GHz CPU, 2GB RAM составляет порядка 1 часа. При использовании ДУ (5) для определения давления под кольцом минимально необходимый шаг расчета составляет 0,01 градус по углу поворота коленчатого вала, а время счета составляет 23 секунды, см. рис. 4.
Точность расчета толщины масляного слоя при этом, при использовании ДУ (5) значительно выше, при этом кольцо не опускается на поверхность цилиндра, см. рис. 4.
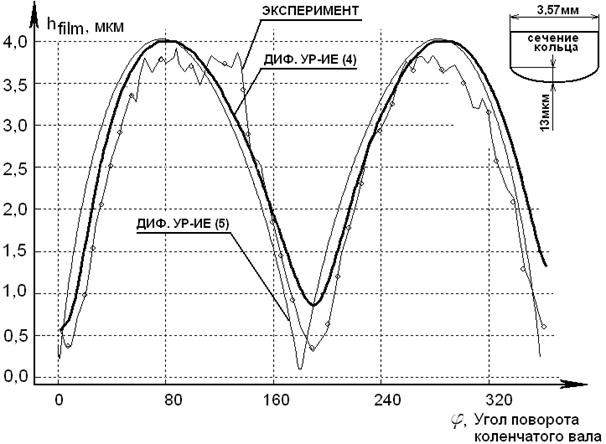
Рис. 4. Сравнение толщины масляной пленки, полученной расчетом и экспериментом [9], при различных величинах внешней нагрузки (F) на поршневое кольцо, равной 3 кг. Коэффициент динамической вязкости масла 75×10-3 Па·с

Рис. 5. Внешний вид экспериментальной установки из работы [9].
В результате проведенной работы был разработан алгоритм расчета динамики кольца, компьютерная программа. Программа была использована для расчета гидродинамики кольца экспериментальной установки. Приведено сравнение экспериментальных и расчетных толщин масляной пленки. Ошибку в расчете толщины слоя масла следует отнести к упрощенному алгоритму обработку зоны с кавитацией под кольцом. Однако, на взгляд автора, для расчета динамики кольца в радиальном направлении двигателя внутреннего сгорания такая точность приемлема, при отсутствии учета влияния профиля канавки под кольцо, вторичной динамики поршня, скручивания кольца и т.д. Для учета этих параметров необходимо заложить в модель геометрию канавок под кольца, расчет теплового и напряженно-деформированного состояния поршня, цилиндра, кольца, а также расчет сил трения между кольцом и цилиндров, распределение давления между кольцом и канавкой в поршне. Такие модели существуют [12, 13, 14] и с успехом эксплуатируются различными исследователями, однако время счета такой программы составляет 10-15 минут для моделирования одного цикла, на компьютере Pentium 4, 3 GHz CPU, 1GB RAM, шаг интегрирования при этом составляет 0,1 градус по углу поворота коленчатого вала [14].
В дальнейшем необходимо совершенствование математической модели, для повышения скорости счета и устойчивости метода. Возможно создание гибридного метода расчета, с переключением используемых ДУ, при расчете давления в слое смазки между ДУ (4) и (5).
В целом, предложенная модель расчета гидродинамики кольца может с успехом использоваться при определении граничных условия теплообмена колец, при моделировании теплообмена цилиндро-поршневой группы.
Литература.
1. Кулешов А.С. Многозонная модель для расчета сгорания в дизеле. Расчет скорости тепловыделения при многразовом впрыске. Вестник МГТУ им. Н.Э. Баумана, специальный выпуск. Серия Машиностроение, стр. 32-45. М.: издательство МГТУ им. Н.Э. Баумана, 2007.
2. Петриченко Р.М. Конвективный теплообмен в поршневых машинах. Л.: «Машиностроение», 1979. 232 с., с ил.
3. Майоров А.В. Разработка методики расчета согласованных температурных полей деталей цилиндропоршневой группы двигателей внутреннего сгорания. Дисс. на соискание степени к.т.н. / МГТУ им. Н.Э. Баумана, - М. 2002. -145л.
4. Аникин С.А. Повышение энергоэкономических показателей четырехтактного дизеля на основе математического моделирования работы и совершенствования конструкции деталей поршневой группы. УДК 621.431.004. Дисс. на соискание уч. степ. канд. техн. наук, Тверь, 1997.
5. Петриченко Р.М. Физические основы внутрицилиндровых процессов в двигателях внутреннего сгорания. Учебное пособие. Л.: Издательство Ленинградского университета, 1983. 244с.
6. Н.А. Слёзкин. Динамика вязкой несжимаемой жидкости. М.: Государственное издательство технико-теоретической литературы. 1955.
7. Кавтарадзе Р.З. Локальный теплообмен в поршневых двигателях. – 2-е изд., испр. и доп. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. – 472 с.
8. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1971, 576 с.
9. Bolander N.W., Steenwyk B.D., Kumar A., Sadeghi F. Film thickness and friction measurement of piston ring cylinder liner contact with corresponding modeling including mixed lubrication. 2004 Fall Technical Conference of the ASME Internal Combustion Engine Division, October 24-27, 2004, Long Beach, California USA.
10. Felter C.L. Lubrication of Piston Rings in Large 2- and 4-stroke Diesel Engine. Technical University of Denmark, Denmark, 2007.
11. Чернышев Г.Д., Хачиян А.С., Пикус В.И. Рабочий процесс и теплонапряженность автомобильных дизелей. – М.: Машиностроение, 1986. – 216 с.: ил.
12. Jocsak J. The Effects of Surface Finish on Piston Ring-pack Performance in Advanced Reciprocating Engine Systems. Master of Science Thesis, MIT. 2005.
13. Smedley G. Piston ring design for reduced friction in modern internal combustion engines. Master of Science Thesis. MIT, 2004.
14. Liang Liu. Modelling the Performance of Piston Ring-Pack with Consideration of Non-Axisymmetric Characteristics of the Power Cylinder System in Internal Combustion Engines. Ph.D. Thesis, MIT, 2005.
Публикации с ключевыми словами: гидродинамика, поршневое кольцо, численный метод, Рунге-Кутта, Рейнольдс
Публикации со словами: гидродинамика, поршневое кольцо, численный метод, Рунге-Кутта, Рейнольдс
Смотри также:
- Проектный анализ аэродинамических схем спускаемых аппаратов капсульной формы численным методом по ньютонианской теории обтекания
- Интегральные уравнения задачи Стефана и их приложение при моделировании оттаивания грунта
- Исследование гидродинамических источников колебаний в двухзавитковом спиральном отводе центробежного насоса НМ1250
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||