научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2011
УДК 004.942
Институт нефтехимии и катализа РАН, г. Уфа
OOO «БашНИПИнефть», г. Уфа
Введение
Термическое гидроалюминирование олефинов до сих пор является одним из наиболее известных и широко применяемых способов синтеза высших алюминийорганических соединений. Однако этот метод отличается рядом специфических свойств, ограничивающих его применение – реакцию необходимо проводить при повышенной температуре, и она применима не ко всем олефинам. В лабораториях Института нефтехимии и катализа РАН под руководством директора института, чл.-корр. РАН У.М. Джемилева проводится экспериментальное изучение альтернативного способа – каталитического гидроалюминирования олефинов изобутилаланами.
Исследование механизма сложных реакций, протекающих в многокомпонентных системах, требует решения двух фундаментальных задач: 1) экспериментальное исследование химического объекта; 2) математическая обработка экспериментальных данных с целью построения и идентификации кинетической модели. При этом большое значение приобретает скорость расчета. Член-корреспондент РАН М.Г. Слинько в одной из своих последних публикаций пишет «Чтобы кинетическая модель могла служить опорой для решения практических вопросов, предварительная кинетическая модель должна быть получена не более, чем за месяц, а полная модель не более, чем за 4 месяца». Для достижения этого требования необходимо использование при расчете современных вычислительных технологий, таких как параллельные вычисления на высокопроизводительных многопроцессорных вычислительных системах (суперкомпьютерах).
1. Химическая постановка задачи
Сложная реакция гидроалюминирования олефинов является частью системы реакций металлокомплексного катализа и представляет собой сложный многостадийный процесс, состоящий из последовательных и параллельных стадий. Поэтому при изучении реакции гидроалюминирования олефинов были выделены и детализированы до элементарных стадий частные реакции с алюминийорганическими соединениями (АОС)
HAlBui2 – диизобутилалюминийгидрид (ДИБАГ),
ClAlBui2 - диизобутилалюминийхлорид (ДИБАХ),
AlBui3 - триизобутиалюминий, ТИБА
и олефинами
гептен-1,
октен-1,
нонен-1,
децен-1.
На этой основе был детализирован общий механизм реакции. В работе рассмотрен общий механизм гидроалюминирования олефинов с ДИБАХ.
Экспериментаторами Института нефтехимии и катализа РАН было предложено несколько механизмов протекания реакции. На начальном этапе изучения реакции удалось выделить частные реакции с АОС и олефинами в виде итоговых уравнений. Далее велись работы по детализации этого механизма до элементарных стадий. В табл. 1 представлен первый этап детализации частных реакций на основании квантово-химических расчетов (схема 1). Например, был сделан вывод, что димер (X1) до вступления в реакцию с АОС разлагается до мономера (X2), который уже реагирует с АОС. Дальнейшие исследования показали, что не только мономер реагирует с АОС, но и сам димер вступает в реакцию с алкеном. Так была получена вторая (более подробная) детализация (табл. 1, схема 2). На основании второй детализации был предложен обобщенный механизм гидроалюминирования олефинов алкилаланами, катализируемого ![]() в присутствии ДИБАХ, на основе элементарных стадий (табл. 1, схема 3).
в присутствии ДИБАХ, на основе элементарных стадий (табл. 1, схема 3).
Таблица 1
Механизмы протекания каталитической реакции гидроалюминирования олефинов
| Схема 1 частные реакции (I детализация) | Схема 2 частные реакции (II детализация) | Схема 3 общая реакция |
ДИБАГ
| X1 X2+X5 | X1 X1+X5→X2+X8 X2+X5→X8 | X9+X15 X9+X18→X10+X13 X9+X10→X2+X11+X13 2X2 X2+X3→X4+X5 X1+X5→X2+X8 X2+X5 X3+X8→X4+2X5 X4+X5→X6+X7 X1+X9→X8+X10 X5+X7→X2 X7+X9→X10 X6+X11 X5+X15 X5+X10
|
ТИБА
| X1 X2+X14→X5+X12 X12→X2+X13 X2+X5 | X1 X2+X14→X8+X13 X1+X14→X2+X8+X13 | |
ДИБАХ
| X1 X2+X9→X5+X10 X9+X10 →X11+X12 X12→X2+X13 X2+X5 | X1 X2+X9→X5+X10 X1+X9→X8+X10 X9+X10→X2+X11+X13 X2+X5→X8 X1+X5→X2+X8 | |
ОЛЕФИНЫ
| X1 X2+X3→X4+X5 X2+X3→X6+X7 X5+X7→X2 X2+X5 | X1 X2+X3→X4+X5 X4+X5→X6+X7 X5+X7→X2 X1+X5→X2+X8 X2+X5→X8 X3+X8→X4+2X5 |
Здесь приняты следующие обозначения:
X1=[Cp2ZrH2·ClAlBu2]2; X2=[Cp2ZrH2·ClAlBu2];
X3=CH2CHR; X4=Cp2ZrCl(CH2CH2R);
X5=HAlBu2 (ДИБАГ); X6=Bu2Al(CH2CH2R);
X7=Cp2ZrHCl; X8=[Cp2ZrH2·HAlBu2·ClAlBu2];
X9=ClAlBu2 (ДИБАХ); X10=[Cp2ZrHCl·ClAlBu2];
X11=l2AlBu; X12=[Cp2ZrHBu·ClAlBu2];
X13=C4H8; X14=AlBu3 (ТИБА);
X15=Сp2ZrCl2; X16=[Cp2ZrH2·HAlBu2·2(ClAlBu2)];
X17=[Cp2ZrH2·HAlBu2·ClAlBu2]; X18=Cp2ZrClBu;
X19=ClBuAl(CH2CH2R); X20=Cp2ZrHBu∙ClAlBu2, Bu=C4H9, Cp=C5H5.
2. Математическое описание химической реакции
При математическом моделировании химических реакций необходимо учитывать, что для одинаковых стадий в разных механизмах реакций кинетические параметры должны быть одинаковыми (допускается отклонение 10% [1]).
Для описания частных реакций использовалась модель без учета количества катализатора [2] (на основании закона сохранения), так как все эксперименты для частных реакций проводились при одном начальном количестве катализатора [3]. При изучении общей реакции гидроалюминирования олефинов был проведен ряд экспериментов с участием различных олефинов: гептен-1, октен-1, нонен-1, децен-1. Для каждого олефина ставились эксперименты при разных температурах и начальном количестве катализатора. Поэтому было предложено изменить математическое описание химической реакции, вынеся из константы скорости количество катализатора отдельным множителем. В гомогенном катализе скорость реакции пропорциональна концентрации катализатора [4]:
![]() (1)
(1)
где ![]() – стехиометрические коэффициенты;
– стехиометрические коэффициенты; ![]() – скорость j-ой стадии, 1/с;
– скорость j-ой стадии, 1/с; ![]() – количество катализатора, моль;
– количество катализатора, моль; ![]() – объем реакционной смеси, л; J – количество стадий.
– объем реакционной смеси, л; J – количество стадий.
Таким образом, используя математическое описание химических реакций по закону сохранения для частных реакций и модифицированную модель (1), для общей реакции гидроалюминирования олефинов была построена математическая модель реакции гидроалюминирования олефинов для всех механизмов реакции из табл. 1. В табл. 2 приведены кинетические уравнения для механизмов реакции.
Таблица 2
Кинетические уравнения реакции гидроалюминирования олефинов олефинов
| частные реакции (I детализация) | частные реакции (II детализация) | общая реакция |
ДИБАГ
| w1= k1x1-k-1x22 w2= k2x2x5-k-2x8 | w1= k1x1-k-1x22 w2= k2x1x5 w3= k3x2x5 | w1=k13x15x9-k-13x18x11 w2= k14x18x9 w3= k8x10x9 w4= k-1x22- k1x1 w5= k9x2x3 w6= k2x1x5 w7= k3x2x5 w8= k12x8x3 w9= k10x4x5 w10= k6x1x9 w11= k11x7x5 w12= k15x7x9 w13= k16x6x11-k-16x19x9 w14= k17x15x5-k-17x10 w15= k-7x10x5-k7x2x9 |
ТИБА
| w1= k1x1-k-1x22 w2= k3x2x14 w3= k4x12 w4= k2x2x5-k-2x8 | w1= k1x1-k-1x22 w2= k5x2x14 w3= k4x1x14 | |
ДИБАХ
| w1= k1x1-k-1x22 w2= k5x2x9 w3= k6x9x10 w4= k4x12 w5= k2x2x5-k-2x8 | w1= k1x1-k-1x22 w2= k7x2x9- k-7x5x10 w3= k6x1x9 w4= k8x10x9 w5= k3x2x5 w6= k2x1x5 | |
ОЛЕФИНЫ
| w1= k1x1-k-1x22 w2= k7x2x3 w3= k8x2x3 w4= k9x5x7 w5= k2x2x5-k-2x8 | w1= k1x1-k-1x22 w2= k9x2x3 w3= k10x4x5 w4= k11x7x5 w5= k2x1x5 w6= k3x2x5 w7= k12x8x3 |
Квантово-химические исследования [6] показали существование ограничений на константы скоростей стадий реакции, т.е. для первой детализации
![]() (2)
(2)
для второй детализации
![]() (3)
(3)
Эти соотношения необходимо учитывать при проведении расчетов.
3. Организация вычислительного процесса
Исследование сложной химической реакции осуществляется в несколько этапов. Сначала происходит исследование макростадий: измерение концентраций реагирующих веществ, формирование условий проведения эксперимента, планирование механизма протекания реакций. Дополнительные квантово-химические исследования позволяют экспериментаторам детализировать реакцию до элементарных стадий с идентификацией промежуточных веществ. При математическом определении значений кинетических параметров стадий можно также установить, является ли лишней или пропущена та или иная стадия. Совместные исследования реакции математиками и химиками нередко помогают последним при составлении окончательного механизма реакции на основании элементарных стадий. Поэтому при работе необходимо хранить всю информацию о реакции – все предложенные механизмы (макростадии и все этапы детализации), условия проведения экспериментов, экспериментальные и расчетные значения концентраций реагирующих веществ, значения кинетических параметров стадий и другую необходимую информацию для проведения расчетов. Таким образом, для математической обработки данных химических исследований возникла необходимость создания баз данных кинетических исследований.
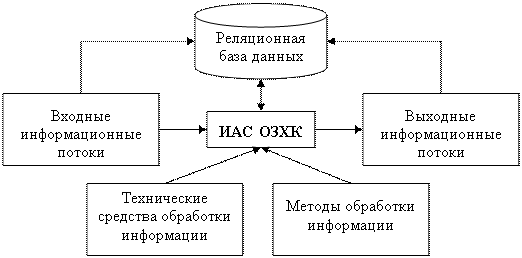
Более подробное изучение химической реакции, ее детализация до элементарных стадий приводят к усложнению задачи. Поэтому необходимо разрабатывать новые способы обработки информации в зависимости от сложности решаемых задач. Эти методы включают в себя: 1) принципы математического моделирования; 2) численные методы и алгоритмы; 3) системы управления базами данных; 4) программирование; 5) проведение многочисленных вычислительных экспериментов. Усложнение задач ведет и к усложнению расчетов, к увеличению времени работы программ. Это вызывает необходимость обновления технических средств обработки информации, увеличения скорости вычислений и объемов хранения данных, использования технологий параллельных вычислений. Все эти процессы являются компонентами информационно-аналитической системы обратных задач химической кинетики (ИАС ОЗХК) (рис. 1) [5].
|
Рис. 1. Структура информационно-аналитической системы обратных задач химической кинетики |
К входным информационным потокам относятся: условия проведения эксперимента; химические формулы веществ, участвующих в реакции; концентрации веществ в начальный момент времени; концентрации веществ в некоторые фиксированные моменты времени (замеры); оценки кинетических параметров (соотношения между константами, интервалы неопределенности некоторых кинетических параметров); предложенные механизмы протекания химических реакций.
К методам обработки информации относятся: алгоритмы решения прямой задачи; параметры управления расчетом обратной задачи; алгоритмы решения обратной задачи; методы построения графиков сравнения расчетных и экспериментальных значений концентраций реагирующих веществ; алгоритмы определения энергии активации стадий реакции. К выходным информационным потокам относятся: расчетные значения концентраций всех веществ, участвующих в реакции, в любой момент времени; расчетные значения энергии активации всех стадий реакции; графики сравнения расчетных и экспериментальных значений концентраций реагирующих веществ; графики изменения скоростей стадий реакции. К техническим средствам обработки информации относятся: экспериментальная установка; промышленный реактор; вычислительные системы (персональный компьютер, многопроцессорная вычислительная система).
Из рис. 1 видно, что входные и выходные информационные потоки образуют единую базу данных. Так как информация о химических реакциях чаще всего предоставляется химиками в виде таблиц [5], используются реляционные базы данных. Для организации базы данных необходимо составить инфологическую модель предметной области. Для этого используется язык ER-диаграмм (рис. 2).
При изучении сложной химической реакции можно выделить несколько перечисленных ниже основных типов сущностей, с экземплярами которых ведется постоянная работа.
|
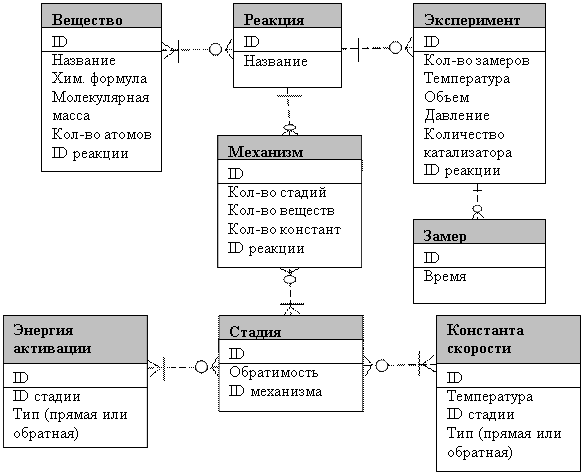
Рис. 2. Инфологическая модель сложной химической реакции |
На рис. 2 построена диаграмма, отражающая связи между основными сущностями в сложной химической реакции. Так, для экземпляра сущности «Реакция» имеется много или один экземпляр сущности «Вещество». Для экземпляра сущности «Вещество» может быть много или ноль экземпляров «Реакция», так как вещество может участвовать во многих реакциях или ни в одной. Для каждой реакции может быть поставлено много или ноль экспериментов, но каждый эксперимент поставлен только для одной реакции. По каждому эксперименту проводится много или ноль замеров, но каждый замер соответствует одному эксперименту. Для каждой реакции можно составить много или ноль механизмов ее протекания, но каждый механизм соответствует только одной реакции. Каждый механизм имеет много или хотя бы одну стадию, а каждая стадия может участвовать во многих или ноль механизмах. Каждая стадия имеет один или несколько (для обратимой стадии) кинетических параметров (констант скоростей, энергий активации), который может участвовать в много или ноль стадиях.
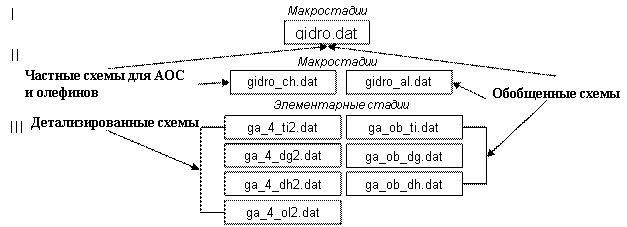
Для упрощения доступа к данным при распараллеливании вычислительного процесса произведена детализация базы данных. Т.е., для реакции каталитического гидроалюминирования олефинов при изучении макростадий база данных была общей. После выделения итоговых уравнений по АОС и олефинам единая база данных была разбита на две базы: для частных схем для АОС и олефинов, и для обобщенной схемы реакции. Дальнейшее детализирование схем позволило разделить базу данных на семь баз – по трем АОС и олефинам для частных реакций и по каждому АОС для обобщенной реакции. Такое разделение базы данных позволяет вести параллельный расчет по этим реакциям с использованием ранее полученных результатов (рис. 3).
|
Рис. 3. Этапы модифицирования баз данных кинетических исследований реакции гидроалюминирования олефинов |
При решении задач химической кинетики большое значение имеет скорость построения кинетической модели, следовательно, возникает вопрос о сокращении времени расчетов. При изучении сложных химических реакций возникают следующие сложности:
– существует несколько гипотетических механизмов протекания реакции, каждый из которых необходимо обработать и выбрать лучший;
– существует несколько наборов экспериментальных данных, полученных при разных условиях (обычно более пяти); для учета погрешности эксперимента обрабатываются все и выбираются два-три лучших, то есть наиболее корректно описывающих экспериментальные данные;
– каждый из кинетических параметров определяется неоднозначно; из-за невозможности измерить концентрации всех веществ, участвующих в реакции (недостаточная информативность эксперимента) экспериментальные данные одинаково хорошо описываются целыми областями пространства кинетических параметров.
Для последовательного решения всех этих задач иногда необходимы существенные затраты времени (от нескольких месяцев до года), что привело авторов к идее последовательно-параллельного ведения расчета [7]. Предлагается сгруппировать задачи, по которым можно вести параллельный расчет, а расчет по этим группам вести последовательно (рис. 4).
Первая группа объединяет все механизмы, предложенные для рассматриваемой реакции, в том числе механизмы реакций, выделенных из общей реакции. Для каждого механизма рассматриваются все эксперименты реакции. И, наконец, по каждому эксперименту производится декомпозиция пространства кинетических параметров на основе принципа геометрического параллелизма.
|
Рис. 4. Модель распараллеливания вычислительного процесса |
Уровень 1. Рассматриваемая задача состоит из групп механизмов реакций, имеющих одинаковые стадии (табл. 1). Поэтому при решении задачи необходимо учитывать, что кинетические параметры для этих стадий должны совпадать. Для отдельных реакций кинетические параметры можно находить параллельно, последовательно определяя сначала общие параметры, удовлетворяющие всем механизмам, в которых они представлены, а затем независимые.
Уровень 2. Для каждого механизма реакций можно параллельно обрабатывать все предложенные эксперименты. Определив константы скоростей при разных температурах, из уравнения Аррениуса [1] методом наименьших квадратов можно получить значения энергий активации для каждой стадии, на основе которых определяются константы скоростей для любой температуры.
Уровень 3. Реализуется принцип геометрического параллелизма, который предполагает декомпозицию расчетной области изменения кинетических констант на подобласти соответственно числу процессоров. Так, для двух кинетических констант строится двумерная плоскость (соответственно, для n констант – n-мерная). Область делится на заданное число подобластей, которые распределяются между процессорами. Каждый процессор решает обратную задачу (минимизирует невязку в своей области методом параболического спуска [2]) только в своих подобластях. После нахождения в каждой подобласти значений констант, минимизирующих функционал невязки [2], исключаются те из них, в который этот функционал имеет наибольшие значения. Из новой области формируются подобласти меньшего размера и процедура повторяется до тех пор, пока не определятся константы, наилучшим образом описывающие эксперимент.
4. Кинетическая модель реакции гидроалюминирования олефинов
После обработки экспериментальных данных для детализации частных реакций были найдены кинетические параметры стадий. Выписаны приведенные значения кинетических параметров относительно начальной мольной плотности реакционной смеси (табл. 3, 4). Результаты первой детализации удовлетворяют условиям (2). Здесь и далее величины ki, k–i измеряются в мин–1, а величина Ej - в ккал/моль.
Таблица 3
Кинетические параметры стадий частных реакций с АОС по первой детализации
T, ºC | K1 | k-1 | k2 | k-2 | k3 | k4 | k5 | k6 | k9 |
2 | 2,6 | 4 | 0,2 | 0,01 | 0,1 | 0,03 | 0,003 | 0,15 | |
-40 | 4 | 5 | 15 | 1,7 | 0,03 | 0,6 | 0,1 | 0,08 | 0,8 |
-20 | 7 | 8,5 | 49 | 10 | 0,08 | 2 | 0,5 | 0,05 | 3,1 |
7 | 13 | 15 | 177 | 69 | 0,2 | 13 | 2,2 | 0,2 | 14 |
30 | 23 | 24 | 434 | 280 | 0,4 | 44 | 6,3 | 0,6 | 45 |
50 | 31 | 33 | 873 | 802 | 0,6 | 110 | 13 | 1,5 | 102 |
Ei | 3,4 | 3 | 6,7 | 10 | 5 | 8,7 | 7,7 | 7,9 | 8 |
Таблица 4
Кинетические параметры стадий частных реакций с олефинами (значения констант k7 (k8) и энергий активаций E7 (E8)) по первой детализации
T, ºC | гептен | октен | нонен | децен |
7 | 0,04 | 0,04 | 0,03 | 0,04 |
30 | 0,07 | 0,08 | 0,07 | 0,09 |
50 | 0,11 | 0,14 | 0,14 | 0,15 |
Ei | 4 | 5,8 | 6 | 5,6 |
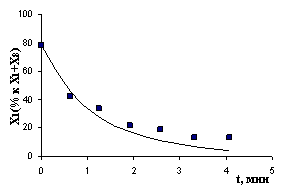
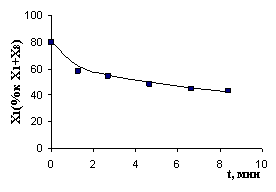
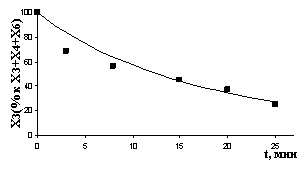
На рис. 5 приведены результаты сравнения экспериментально заданных и рассчитанных по модели (1) с учетом (2) концентраций наблюдаемого вещества для частных реакций с АОС и олефинами по первому этапу детализации. Среднее отклонение расчета от эксперимента для предложенной кинетической модели не превышает 10%. Сравнивая скорости прямой и обратной реакции образования мономерного комплекса X2 из X1, можно сделать вывод, что в интервале температур -60÷500С равновесие смещено в сторону димерной формы, однако, с увеличением температуры доля X2 в смеси возрастает. Самой быстрой оказалась стадия перехода комплекса X2 в тригидридный комплекс X8, а равновесие X2 ↔ X8 сильно смещено в сторону тригидридного комплекса, особенно при низких температурах. В реакции гидрометаллирования олефинов комплексом X1 лимитирующими оказались равновероятные стадии взаимодействия мономерного комплекса X2 с алкенами. По-видимому, высокая скорость гидрометаллирования обеспечивается существованием обратной реакции перехода комплекса X8 в активный по отношению к олефинам мономер.
а) 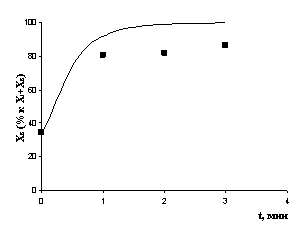
| б)
| ||||
в) 
| г)
| ||||
Рис. 5. Экспериментальные и расчетные результаты (детализация I): а) реакция с НAlBui2, T= -600C; б) реакция с ClAlBui2, T = -200C; в) реакция с AlBui3, T = -200C; г) реакция с деценом-1, T = 70C | |||||
Соотношение (2) для детализации I выполняется в рассматриваемом экспериментатором интервале температур. Построив на основе уравнения Аррениуса зависимость ln(k) от 1/T для k1 и k-1, можно увидеть, для каких температур это соотношение будет нарушено (рис. 6).

Из рис. 6 видно, что графики функций ln(k1), ln(k-1) пересекаются в точке ![]() , левее которой соотношение (2) нарушается. При этом T = 400 K = 127°C, т.е. для температур выше 127°C соотношение (2) нарушается. Поэтому был сделан вывод, что первая детализация частных реакций не в полной мере характеризует экспериментальные и теоретические данные.
, левее которой соотношение (2) нарушается. При этом T = 400 K = 127°C, т.е. для температур выше 127°C соотношение (2) нарушается. Поэтому был сделан вывод, что первая детализация частных реакций не в полной мере характеризует экспериментальные и теоретические данные.
Для второй детализации частных реакций выписаны приведенные значения кинетических параметров относительно начальной мольной плотности реакционной смеси (табл. 5, 6).
Таблица 5
Кинетические параметры стадий частных реакций с АОС по второй детализации
T, ◦С | k1 | k-1 | k2 | k3 | k4 | k5 | k6 | k7 | k-7 | k8 |
-65 | 0,2 | 0,7 | 0,17 | 3,5 | 0,03 | 0,0002 | 0,0005 | 0,01 | 0,3 | 0,24 |
-60 | 0,28 | 1 | 0,22 | 4,5 | 0,04 | 0,0003 | 0,001 | 0,02 | 0,5 | 0,4 |
-40 | 0,6 | 4 | 0,8 | 21 | 0,1 | 0,001 | 0,01 | 0,1 | 5,5 | 3,7 |
-20 | 1,4 | 14 | 2 | 69 | 0,2 | 0,006 | 0,1 | 0,4 | 37 | 23 |
-10 | 2 | 24 | 3 | 117 | 0,25 | 0,01 | 0,2 | 0,8 | 86 | 51 |
7 | 3,4 | 55 | 6 | 266 | 0,4 | 0,03 | 1 | 2 | 312 | 177 |
Ei | 4,5 | 7 | 6 | 7 | 4 | 8 | 12 | 8 | 11 | 10 |
Таблица 6
Кинетические параметры стадий частных реакций с олефинами по второй детализации
Олефин | Т, ◦С | k9 | k10 | k11 | k12 |
Гептен | 5 | 0,2 | 660 | 0,62 | 0,0009 |
7 | 0,3 | 678 | 0,65 | 0,001 | |
12 | 0,35 | 695 | 0,7 | 0,002 | |
Ei | 14 | 1 | 3,5 | 22 | |
Октен | 10 | 0,3 | 720 | 0,7 | 0,002 |
12 | 0,4 | 786 | 0,7 | 0,003 | |
Ei | 14 | 7 | 6 | 27 | |
Нонен | 5 | 0,2 | 745 | 0,6 | 0,001 |
12 | 0,3 | 802 | 0,7 | 0,002 | |
Ei | 11 | 1,7 | 3,5 | 13 | |
Децен | 5 | 0,28 | 223 | 0,62 | 0,002 |
7 | 0,29 | 400 | 0,65 | 0,0025 | |
Ei | 8 | 25 | 3,5 | 11 | |
Результаты второй детализации удовлетворяют условиям (3): константа обратной реакции значительно больше константы прямой реакции, k4 больше чем k2, k11 много больше k14, что корректно описывает эксперимент.
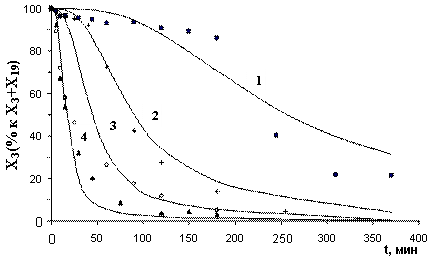
Результаты сравнения эксперимента и расчета для всех АОС и олефинов представлены на рис. 7.
а)
| б)
|
в) | г)
|
Рис. 7. Экспериментальные и расчетные результаты (детализация II): а) реакция с НAlBui2, T= -550C; б) реакция с ClAlBui2, T = -100C; в) реакция с AlBui3, T = -400C; г) реакция с октеном, T = 120C | |
Отклонение расчетных результатов от экспериментальных не превышает 8,5 %.
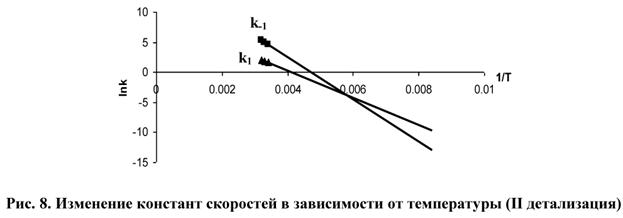
налогично предыдущим вычислениям, для выяснения пределов соблюдения соотношения (3) построим зависимость ln(k) от 1/T для k1 и k-1 (рис. 8).
Из рис. 8 видно, что графики функций ln(k1) и ln(k-1) пересекаются в точке ![]() , правее которой соотношение (3) нарушается.
, правее которой соотношение (3) нарушается.
При этом T=173 K=-100°C, т.е. для температур ниже (-100)°C соотношение (3) нарушается. Такие температуры встречаются крайне редко при постановке экспериментов, поэтому можно считать, что вторая детализация частных реакций достаточно хорошо характеризует экспериментальные и теоретические данные.
Для общей реакции гидроалюминирования олефинов в присутствии ДИБАХ построены кинетические модели без учета количества катализатора и с учетом количества катализатора. Сделан вывод о том, что модель (1), учитывающая количество катализатора, лучше описывает реакцию, и практически все кинетические параметры стадий, определенные по этой модели, совпадают с соответствующими кинетическими параметрами частных реакций (исключение составляет k9(E9)). В табл. 7 представлены кинетические параметры стадий общей реакции, полученные с использованием модели (1). Представлены приведенные константы относительно начальной мольной плотности реакционной смеси. Результаты расчета и эксперимента для общей реакции гидроалюминирования олефинов в присутствии диизобутилалюминийхлорида по модели c учетом катализатора (xкт – катализатор) представлены на рис. 9, 10. Отклонение расчетных результатов от экспериментальных данных не превышает 10%.
Таблица 7
Кинетические параметры стадий реакции с учетом количества катализатора
T◦C | 20 | 30 | 40 | E (октен) | ||||||
Олефин | Гептен | Октен | Нонен | Децен | Октен | |||||
Xкт | 0,18 | 0,18 | 0,3 | 0,5 | 1 | 0,18 | 0,18 | 0,18 | 0,18 | |
k1 | 5 | 5 | 8 | 13 | 27 | 5 | 5 | 6 | 8 | 4,5 |
k-1 | 97 | 97 | 162 | 270 | 540 | 97 | 97 | 144 | 210 | 7 |
k2 | 10,7 | 10,4 | 18 | 30 | 60 | 11 | 11 | 15 | 20 | 5,8 |
k3 | 467 | 454 | 778 | 1297 | 2595 | 467 | 467 | 692 | 1003 | 7 |
k6 | 2,9 | 2,8 | 5 | 8 | 16 | 3 | 3 | 6 | 11 | 12 |
k7 | 4 | 4 | 6 | 10 | 20 | 4 | 4 | 6 | 9 | 8 |
k-7 | 757 | 757 | 1258 | 2082 | 4074 | 757 | 757 | 1422 | 2564 | 11 |
k8 | 412 | 412 | 687 | 1146 | 2293 | 412 | 412 | 754 | 1325 | 10,6 |
k9 | 313 | 314 | 539 | 899 | 1842 | 1048 | 2072 | 932 | 1865 | 0,8 |
k10 | 734 | 1072 | 1840 | 3066 | 6131 | 871 | 2626 | 1644 | 2387 | 7 |
k11 | 0,86 | 0,98 | 2 | 3,5 | 7 | 0,98 | 0,98 | 1,4 | 4,7 | 6,6 |
k12 | 0,006 | 0,01 | 0,02 | 0,03 | 0,06 | 0,004 | 0,006 | 0,05 | 0,2 | 26 |
k13 | 0,001 | 0,001 | 0,003 | 0,005 | 0,008 | 0,001 | 0,001 | 0,005 | 0,04 | 31 |
k-13 | 0,3Е-06 | 0,3Е-06 | 0,3Е-06 | 0,5Е-06 | 0,1Е-05 | 0,3Е-06 | 0,3Е-06 | 0,5E-06 | 0,3Е-06 | 1 |
k14 | 0,3 | 0,3 | 0,5 | 0,9 | 1,8 | 0,3 | 0,3 | 0,7 | 1,3 | 13 |
k15 | 0,426 | 0,414 | 0,77 | 1,284 | 2,57 | 0,426 | 0,426 | 1,8 | 8 | 27 |
k16 | 383 | 106 | 182 | 303 | 607 | 499 | 1699 | 376 | 800 | 18 |
k-16 | 0,3Е-06 | 0,3Е-06 | 0,3Е-06 | 0,5Е-06 | 0,1Е-05 | 0,27Е-06 | 0,26Е-06 | 0,1Е-05 | 0,2Е-05 | 19 |
k17 | 0,2Е-05 | 0,2Е-05 | 0,4Е-05 | 0,6Е-05 | 0,1Е-04 | 0,24Е-05 | 0,24Е-05 | 0,5Е-05 | 0,1Е-04 | 14 |
k-17 | 0,04 | 0,04 | 0,07 | 0,1 | 0,2 | 0,04 | 0,04 | 0,02 | 0,03 | 10 |
|
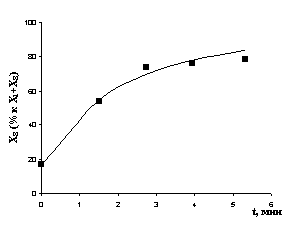
Рис. 9. Экспериментальные и расчетные результаты для общей реакции с октеном, T=20°C: 1) Xкт=0,18 ммоль; 2) 0,3 ммоль; 3) 0,5 ммоль; 4) 1 ммоль (с учетом катализатора) |
|
Рис. 10. Экспериментальные и расчетные результаты для общей реакции с октеном, Xкт=0,18 ммоль: 1) T=20°C; 2) 30°C; 3) 40°C (с учетом катализатора) |
На рис. 11 представлена кинетическая модель обобщенной реакции каталитического гидроалюминирования олефинов с помощью ДИБАХ. Значения кинетических параметров обобщенной реакции, полученные посредством математического моделирования, подтверждают выводы, полученные квантово-химическим подходом [6]. Таким образом, в рассматриваемом случае макрокинетика (экспериментально-расчетные исследования на уровне молекул) обосновывает выводы микрокинетики (теоретические исследования на уровне атомов). Построенная математическая модель реакции позволяет определить кинетические параметры реакции в условиях, которые сложно создать экспериментально.
|
Рис. 11. Кинетическая модель обобщенной реакции каталитического гидроалюминирования олефинов с ДИБАХ (октен, T=20°C, Xkt = 0,18 ммоль) |
Из рис. 11 видно, что первоначально Сp2ZrCl2 взаимодействует с молекулой ClAlBu2i с образованием Cp2ZrClBu (E=31 ккал/моль). Эта стадия обладает наибольшим активационным барьером. В начальный момент времени наблюдается низкая скорость межлигандного обмена между исходными веществами, благодаря чему в реакции гидроалюминирования олефинов с ДИБАХ наблюдается индукционный период – необходимо время на образование комплекса (15), который является ключевым и отвечает за гидрометаллирование олефинов. Далее включается каталитический цикл. При увеличении начального количества катализатора увеличивается скорость межлигандного обмена, что ускоряет образование (15) для которого включается каталитический цикл, что приводит к уменьшению индукционного периода реакции гидроалюминирования олефинов с ДИБАХ.
Реакция димеризации комплекса (15) (E=7,02 ккал/моль) и взаимодействие его же с очередной молекулой ДИБАГ (E=7 ккал/моль) практически равновероятны. Но для гидроалюминирования олефинов с ДИБАХ ДИБАГ не является исходным веществом, а образуется в ходе реакции, в малых количествах. Поэтому более вероятна димеризация комплекса (15), в результате чего образуется комплекс (6). Соединение (15) находится в мономер-димерном равновесии с бициркониевым комплексом (6). Комплекс (15) и (6) могут взаимодействовать с молекулой ДИБАГ с образованием тригидридного комплекса (7).
Принимая во внимание активационные барьеры реакций взаимодействия комплекса (12) с ДИБАГ (E=6,62 ккал/моль) и ДИБАХ (E=26,7 ккал/моль), можно сделать вывод, что более вероятно протекание реакции Cp2ZrHCl с HAlBu2i, что приводит к образованию мономера Cp2ZrH2·ClAlBu2i.
Гидрометаллирующая активность комплексов уменьшается в ряду (12)(E=6,6 ккал/моль)>(15)(E=7 ккал/моль)>(7)(E=26 ккал/моль). Тогда в каталитическом процессе скорость будут определять эффективная концентрация и взаимное отношение компонентов (12), (15), (7).
Учитывая активационные параметры реакций, первоначально происходят превращения (12)→(15)→(7). Однако комплекс (7) обладает меньшей активностью, так как активационный барьер его реакции с олефином значительно выше (E=26 ккал/моль) относительно (12) (E=6,6 ккал/моль) и (15) (E=7 ккал/моль). Ранее, в первой детализации, комплекс (7) считался неактивным по отношению к олефинам.
5. Математическое моделирование индукционного периода
На графиках, представленных на рис. 9, 10, наблюдается индукционный период. Для определения характера индукционного периода был проведен вычислительный эксперимент. Взяв за эталонные значения констант скоростей при Xkt = 0,3 ммоль (табл. 7), был определен индукционный период для различного начального количества катализатора. Исследования проводились для следующих значений количества катализатора, ммоль: 0,01<=Xkt<=0,09 с шагом 0,01; 0,1<=Xkt<=0,9 с шагом 0,1; 1<=Xkt<=5 с шагом 0,5.
Для любого начального количества катализатора (Xkt) константы скоростей определяются следующим образом:
![]()
Зная константы скоростей, можно определить концентрацию наблюдаемого вещества X3 в любой момент времени (tl), решив прямую задачу, т.е. задачу Коши для системы обыкновенных нелинейных дифференциальных уравнений с заданными начальными условиями с фиксированными ![]() и неизвестными
и неизвестными ![]() . Обозначив зависимость концентрации вещества X3 от времени через x(t), получим
. Обозначив зависимость концентрации вещества X3 от времени через x(t), получим
![]()
где tl – время, с.
Исходя из определения индукционного периода [8] и производной функции, можно считать, что индукционный период функции равен t, если
![]() или
или ![]()
Как видно из рис. 12, имеет место высокая параметрическая чувствительность продолжительности индукционного периода от начального количества катализатора. С уменьшением количества катализатора закономерно увеличивается индукционный период. Количество катализатора, большее 2 ммоль, несущественно влияет на индукционный период.
|
Рис. 12. Зависимость длительности индукционного периода (Tind) от количества катализатора (для 0,09≤Xкт≤2 ммоль) |
На рис. 13 показана скорость расходования наблюдаемого вещества в зависимости от количества катализатора. Здесь ![]()
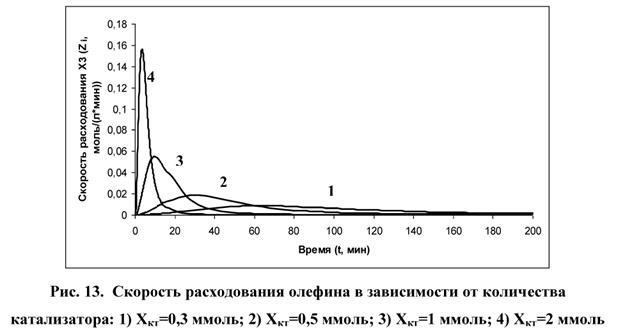
Из рис. 13 следует, что с увеличением количества катализатора скорость расходования наблюдаемого вещества (X3) увеличивается. Следуя определению индукционного периода, амплитуда полученных графиков отображает Δl. Чем больше количество катализатора, тем меньше Δl, то есть тем меньше продолжительность ускорения расходования наблюдаемого вещества.
На рис. 14 представлена зависимость максимальной скорости расходования наблюдаемого вещества Zmax от Tind. С увеличением длительности индукционного периода величина Zmax уменьшается по гиперболическому закону.
|
Рис. 14. Зависимость максимальной скорости расходования наблюдаемого вещества от индукционного периода (для 0,6<=Xкт<=5 ммоль) |
Вычислив коэффициенты этого уравнения, прологарифмировав его и проведя расчеты для двух значений количества катализатора, можно определить значение Zmax для любого Tind и наоборот (рис. 15).
Из рис. 15 видно, что с ростом молекулярной цепи олефинов происходит небольшое увеличение индукционного периода, причем для группы нонен-децен в большей степени, чем для группы гептен-октен. Однако внутри группы наблюдается обратная зависимость, что говорит о необходимости проведения экспериментов для других олефинов с целью объяснения данного явления.
6. Заключение
В ходе исследования выявлен внутренний параллелизм задачи построения механизма реакции каталитического гидроалюминирования олефинов, на основе которого предложен трехуровневый метод распараллеливания вычислительного процесса. Разработана информационно-аналитическая система обратных задач, включающая базы данных детализированных и обобщенных стадий. Построена кинетическая модель частных реакций гидроалюминирования олефинов, по которой для первого и второго этапа детализации частных реакций определены константы скоростей и энергии активации. На основе второй детализации частных реакций определены кинетические константы общего механизма гидроалюминирования олефинов с ДИБАХ, в том числе для экспериментов с индукционным периодом. Определен характер индукционного периода для общей реакции гидроалюминирования олефинов с Д ИБАХ. Установлено и количественно оценено увеличение индукционного периода с уменьшением концентрации катализатора. Определены максимальные значения скорости расходования наблюдаемого вещества в зависимости от количества катализатора.
В развитие работы планируется провести дополнительные экспериментальные исследования с целью более глубокого понимания зависимости скорости расходования наблюдаемых веществ от индукционного периода в реакции гидроалюминирования олефинов. Разработанную методологию параллельных вычислений планируется реализовать для остальных реакций металлокомплексного катализа, исследуемых в ИНК РАН, в первую очередь для карбо- и циклоалюминирования олефинов, и на основе вычислительного эксперимента построить кинетические модели указанных реакций и включить их в разрабатываемую авторами информационно-аналитическую систему обратных задач химической кинетики.
Литература
1. Слинько М.Г. Основы и принципы математического моделирования каталитических процессов. Новосибирск: Ин-т катализа им. Борескова СО РАН, 2004. 488 с.
2. Спивак С.И., Губайдуллин И.М., Вайман Е.В. Обратные задачи химической кинетики. Уфа: РИО БашГУ, 2003. 110 с.
3. Парфенова Л.В., Печаткина С.В., Халилов Л.М., Джемилев У.М. Исследование механизма гидроалюминирования олефинов алкилаланами, катализируемого Cp2ZrCl2 // Изв. РАН, Сер.хим. 2005. Т. 2. С. 311-322.
4. Крылов О.В. Гетерогенный катализ. Москва: ИКЦ «Академкнига», 2004. 679 с.
5. Губайдуллин И.М., Спивак С.И. Информационно-аналитическая система обратных задач химической кинетики // Системы управления и информационные технологии. 2008. ╧1.1(31). С. 150-153.
6. Панкратьев Е. Ю., Тюмкина Т. В., Халилов Л. М., Парфёнова Л. В., Хурсан С. Л., Джемилев У. М. DFT моделирование образования Al,Zr-комплекса как ключевого интермедиата в реакции каталитического гидроалюминирования олефинов // Сборник тезисов V всероссийской конференции «Молекулярное моделирование». Москва, 2007. С. 84.
7. И.М. Губайдуллин, Ю.Б. Линд. Информационно-аналитическая система решения обратных задач химической кинетики на основе современных высокопроизводительных вычислений // Вестник Омского университета. 2010. ╧ 4(58). С. 137-146.
8. Хилько А.В., Спивак С.И., Губайдуллин И.М., Парфенова Л.В. О математическом моделировании индукционного периода химических реакций // Системы управления и информационные технологии. 2008. ╧1.2(31). С. 264-267.
Публикации с ключевыми словами: параллельные вычисления, химическая кинетика, обратная задача, детализация реакции, гидроалюминирование олефинов, индукционный период
Публикации со словами: параллельные вычисления, химическая кинетика, обратная задача, детализация реакции, гидроалюминирование олефинов, индукционный период
Смотри также:
- 77-48211/483201 Моделирование химических превращений при выбросе промышленных газов в атмосферу
- Вопросы обучения технологиям параллельных вычислений и использования распараллеленных программных средств на удаленных компьютерах
- Возможности применения параллельных методов вычисления в системе программирования на языке S-FLOGOL
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||