научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 07, июль 2009
Развитие информационных систем и, как следствие, накопление огромного количества информации поставило на новый уровень задачи анализа данных. Среди прочих задач одной из актуальных является задача экстраполяции экономических и физических процессов, объединенных во множество псевдослучайных процессов.
В силу того, что задача экстраполяции псевдослучайных процессов не является новой, то до текущего момента была проделана серьезная работа в данной сфере. В соответствии с [1, 2, 3] все алгоритмы можно разделить на несколько групп: регрессионные модели [4,5,6] (линейная регрессия, АРПСС [3]); вероятностные модели [1,2]; метод группового учета аргументов [1]; нейронные сети [1]; классификационно-регрессионные деревья [8]; базовая авторегрессия с условной гетероскедастичностью [7]. Большинство приведенных методов предполагают не только поиск закономерностей внутри процессов, но и учет влияния внешних факторов [3,4,5,6,7,8].
В представленной научной работе в отличие от классических регрессионных методов анализ псевдослучайных процессов основан на предположении того, что существует множество факторов, оказывающих влияние на значения процесса, однако определить степень влияния каждого фактора невозможно по причине объема, конфиденциальности, трудностей в измерении информации. Авторами вводится предположение, что если общее влияние всего множества факторов в какой-то период времени привело к тому, что процесс имел определенный профиль, то существует или когда-то случится такой период времени, когда суперпозиция влияния всего множества факторов приведет к тому, что процесс будет иметь профиль подобный исходному. Данное предположение вводится на базе принципа Дирихле для псевдослучайного процесса с конечным числом внутренних состояний, значение которого рано или поздно повторится.
Пусть существует псевдослучайная последовательность ![]() длиной T. Тогда введем обозначение
длиной T. Тогда введем обозначение
![]() , (1)
, (1)
вектор длины M, лежащий внутри исходного X(t) началом которого является момент времени t=N. В качестве меры подобия двух векторов внутри одной псевдослучайной последовательности используем линейную корреляцию Пирсона.
![]() (2)
(2)
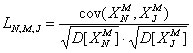 , (3)
, (3)
где ![]() - ковариация исходных векторов, а
- ковариация исходных векторов, а ![]() и
и ![]() их дисперсии. Причем при N=J
их дисперсии. Причем при N=J ![]() .
.
Тогда функция подобия
![]() (4)
(4)
возвращает вектор значений модулей коэффициентов линейной корреляции со всеми векторами длины M, лежащими левее на оси времени. Результирующий вектор L(i) имеет длину N-1 и назовём вектор подобия. Тогда вектор ![]() , соответствующий максимуму вектору подобия
, соответствующий максимуму вектору подобия
![]() (5)
(5)
назовем максимумом подобия для исходного вектора ![]() .
.
Далее введем предположение о том, что если ![]() и
и ![]() имеют высокое подобие, то есть модуль линейного коэффициента корреляции Пирсона близок к 1, то вектора
имеют высокое подобие, то есть модуль линейного коэффициента корреляции Пирсона близок к 1, то вектора ![]() и
и ![]() будут также иметь высокое подобие. Данное предположение назовем предположением о подобии. На основании предположения о подобии решается задача экстраполяции вектора
будут также иметь высокое подобие. Данное предположение назовем предположением о подобии. На основании предположения о подобии решается задача экстраполяции вектора ![]() в точках
в точках ![]() по максимуму подобия.
по максимуму подобия.
В связи с тем, что в качестве меры подобия был использован коэффициент линейной корреляции, то экстраполированные значения будут определяться следующим образом:
![]() , (6)
, (6)
где А - матрица линейных коэффициентов размерностью 2х1, а ![]() часть исходной последовательности
часть исходной последовательности ![]() , определяемая исходя из равенств, представленных ниже. В частном случае при
, определяемая исходя из равенств, представленных ниже. В частном случае при ![]() , то есть, в случае, когда необходимо экстраполировать процесс лишь в одной точке, равенство (6) принимает вид простой линейной зависимости:
, то есть, в случае, когда необходимо экстраполировать процесс лишь в одной точке, равенство (6) принимает вид простой линейной зависимости:
![]() , (7)
, (7)
В общем случае при необходимости экстраполяции P точек для определения матрицы A, возьмем вектор ![]() и найдем его максимум подобия.
и найдем его максимум подобия.
![]() (8)
(8)
Считаем, что для векторов ![]() и
и ![]() верно равенство (9), которое расшифровывается в выражении (10)
верно равенство (9), которое расшифровывается в выражении (10)
![]() , (9)
, (9)
 , (10)
, (10)
где вектор ![]() - вектор ошибок аппроксимации. Аппроксимация
- вектор ошибок аппроксимации. Аппроксимация
![]() , (11)
, (11)
позволяет определить матрицу A, решая уравнение (11):
![]() (12)
(12)
В соответствии с предположением о подобии в качестве ![]() берем вектор
берем вектор ![]() , то есть вектор, лежащий на оси времени сразу за вектором максимума подобия. Положения векторов наглядно представлены на рис 1.
, то есть вектор, лежащий на оси времени сразу за вектором максимума подобия. Положения векторов наглядно представлены на рис 1.
 |
| Рис 1. Положения векторов |
По предложенному алгоритму решается задача экстраполяции псевдослучайной последовательности ![]() в точках
в точках ![]() по максимуму подобия.
по максимуму подобия.
Отметим также, что в основе экстраполяции лежит линейная регрессия (6), а, следовательно, возможен учет влияния внешних факторов на исследуемый процесс в случаях, когда данный учет необходим. Тогда ![]() , где
, где
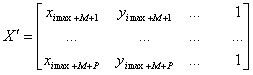 , (13)
, (13)
где Y - вектор значений независимой переменной. Однако в данном случае в качестве меры подобия необходимо использовать квадрат множественного коэффициента корреляции [9] вместо линейной корреляции Пирсона. Алгоритм экстраполяции с учетом внешних факторов, а также поведение ошибки будет опубликован в одной из следующих статей.
В заключение статьи приводим примеры реализации экстраполяции псевдослучайных кривых.
1) Экстраполяция кривой фьючерсных цен на природный газ на Нью-Йоркской товарной бирже (NYMEX, www.nymex.com) за период с 01.10.2008 по 01.05.2009 (7 месяцев) на 24 значение вперед (почасовые значения на следующий день) - средняя ошибка экстраполяции составила 2,36%.
2) Экстраполяция Торгового Графика (потребления) по Сибирской ценовой зоне ОРЭМ (Оптовый рынок электроэнергии и мощности, www.atsenergo.ru) за период с 01.03.2008 по 01.03.2009 (12 месяцев) на 24 значения вперед (почасовые значения на следующий день) - средняя ошибка экстраполяции составила 1.40%.
3) Экстраполяция цен РСВ (рынок на сутки вперед) по Европейской ценовой зоне ОРЭМ за период с 01.01.2009 по 28.02.2009 (2 месяца) на 24 значения вперед (почасовые значения на следующий день) - средняя ошибка составила 7.94%.
Оценка точности экстраполяции производилось при помощи MAPE (mean absolute percentage error) - средняя абсолютная ошибка в процентах, определяемая по формуле:
![]() (14)
(14)
В статье рассмотрен метод экстраполяции псевдослучайных процессов на основании максимума подобия, а также продемонстрированы некоторые результаты, которые позволяют говорить о состоятельности данного подхода. В дальнейших статьях планируется представить подробный анализ результатов экстраполяции различных псевдослучайных процессов.
Список литературы
1. Э.Е. Тихонов, "Прогнозирование в условиях рынка", Невинномысск, 2006 г.
2. В. И. Суслов, Н. М. Ибрагимов, Л. П. Талышева, А. А. Цыплаков, "Эконометрия", И: Новосибирский государственный университет, 2005 г.
3. А.А. Грешилов, В.А. Стакун, А.А. Стакун, "Математические методы построения прогнозов", И: Москва, Радио и связь, 1997 г.
4. Дж. Бокс, Г. Дженкинс, "Анализ временных рядов", 1967 г.
5. Prajakta S. Kalekar, "Time series Forecasting using Holt-Winters and Exponential Smoothing", Kanwal Rekhi School of Information Technology, 2004
6. Uwe Hassler and J?urgen Wolters, "Autoregressive Distributed Lag Models and Cointegration", 2005
7. Reinaldo C. Garcia, "A GARCH Forecasting Model to Predict Day-Ahead Electricity Prices", German Institute of Economic Research, DIW (Berlin), Germany, 2003
8. M. Sc. Jingfei Yang, "Power System Short-term Load Forecasting", Elektrotechnik und Informationstechnik der Technischen Universit?t Darmstadt, 2006
9. Herve Abdi, Multiple Correlation Coefficient, The University of Texas at Dallas, 2007
Публикации с ключевыми словами: информационные технологии, псевдослучайные процессы
Публикации со словами: информационные технологии, псевдослучайные процессы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



