научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 8, август 2008
УДК 621.835
Милевская Т. В.
МГТУ им. Н.Э. Баумана
Кафедра «Технологии обработки давлением»
Научный руководитель: д.т.н., проф. Головин А.А.
Введение
Обычно рекомендуется применять эвольвентные зубчатые передачи с передаточным отношением u = 2…3 [1]. Однако в ряде случаев применяются передачи с большим передаточным отношением. На фиг.1 показаны примеры таких передач [2, 3, 4]. На рис.1а приведена кинематическая схема пресса “Toledo”. На фиг.1б приведен фрагмент исходного профиля зубьев промежуточной силовой открытой эвольвентной зубчатой передачи (u = 6,33; z1 = 15; z2 = 95; m = 26 мм). На фиг.1в приведен фрагмент зубчатой передачи фирмы AEG моторного вагона электропоезда (u = 3,69; z1 =19; z2 = 70; m = 9 мм). Мы специально взяли примеры, в которых передачи существенно изношены. Обе передачи работали в скверных эксплутационных условиях: передача пресса“Toledo” – открытая, работала в условиях заготовительного производства; передача фирмы AEG – закрытая, но с плохим отводом продуктов износа. Существенным фактором является так же то, что механические свойства шестерни в обоих случая выше, чем у колеса.

Рис. 1. Примеры зубчатых передач с большим передаточным отношением.
В данной статье анализ износа проводится на макроскопическом уровне. Такой подход позволяет при сравнительно грубом моделировании получить простую, но правдоподобную модель. Именно упрощенная трактовка и применение основополагающих закономерностей вместо их поиска представляет интерес для инженера. В соответствии с классификацией, приведенной в [4, 5], на уровне элементарных имитационных моделей можно попытаться объяснить следующие виды износа: непрерывный износ, выкрашивание и истирание. Интуитивно ясно, что процесс износа вряд ли удастся описать какой-либо одной моделью. Однако на каждом этапе можно выделить фактор или группу факторов, наиболее существенно влияющих на процесс. В основу моделирования положено два критерия: геометрический аналог контактного напряжения (s) и геометрический аналог диссипации энергии, учитывающий путь скольжения сопрягаемых профилей (s·vск /vt).. Условия, в которых работают зубчатые передачи, приведенные на рис. 1 в соответствии с [2, 3, 4] можно сформулировать следующим образом:
- трение в паре велико; характеристики материала и поверхность зубьев шестерни лучше, чем колеса;
- ожидаемый износ поверхности шестерни – смятие - выкрашивание; колеса – истирание.
В этом случае доминирующим фактором износа шестерни является контактное напряжение sк [ 3]:
 (1)
(1)
где r1, r2 – радиусы сопрягаемых эвольвент; r1+r2=N1N2.
Ему соответствует геометрический аналог контактного напряжения s [3, 4, 5]
s = sQ sr = sк / B, (2)
где sQ =Qn/Qnнб - аналог нормальной реакции в ВП;
 -
аналог контактного напряжения в точке контакта при единичной нагрузке;
-
аналог контактного напряжения в точке контакта при единичной нагрузке;
s = sQ sr - аналог контактного напряжения в точке контакта.
Доминирующим фактором начальной фазы износа колеса по истиранию является диссипация энергии (мощности) sк·vск. Последующие стадии зависят от износа в особых точках на поверхности зуба колеса [3, 4, 5]. Геометрическим аналогом износа колеса по истиранию является (s·vск /vt), учитывающий путь скольжения профиля. Потери на преодоление трения качения незначительны и поэтому не учитываются.
Здесь
vск – аналог скорости скольжения в ВП;
vτ1,2 – аналог тангенциальных составляющих скоростей контактирующих точек;
(s vск) – аналог диссипации энергии в точке контакта.
Соответственно, износ шестерни
wшест ~ s,
износ колеса
wк ~ s·vск /vt.
1. Свойства эвольвентной зубчатой передачи.
На рис.2 приведены эпюры износа шестерни и колеса двух передач с различным передаточным отношением. На рис.2а приведены эпюры износа передачи c большим передаточным отношением (пресс “Toledo”; u = 6.33). На рис.2б – аналогичные эпюры для передачи общего назначения [8] (u = 1.5). Здесь N1N2 - линия зацепления, P - полюс зацепления, B1; B2 - точки входа пары в зацепление и выходе из него, B1*; B2* - точки пересопряжения зубьев.
Из фиг.2б видно, что зона зацепления передачи с небольшим передаточным отношением соответствует области минимальных значений sc и области минимальных значений (s·vск /vt ). Поэтому при расчете на контактную прочность расчет удобно проводить по напряжениям в полюсе зацепления [8]. В случае передачи с большим передаточным отношением зона зацепления смещается к началу линии зацепления – т.N1. Соответственно sк и (sv) в тт. B1 и B1* существенно возрастают. Поэтому расчет на контактную прочность следует проводить по напряжениям в тт.B1, B1* .Однако для всех передач типа B1 – P – B2 характерно, что износ по (sv) имеет место в окрестности т. P, а в самой т.P – по s, то есть полюс зацепления является особой точкой.

Рис. 2. Сравнение эпюр износа передач с различным передаточным отношением.
На рис.3 представлена имитационная модель износа зубчатой пары типа B1 – P – B2, описанная в [3]. Начальная стадия износа и два-три шага износа достаточно просто поддаются формализации. Первый шаг делается из предположения, например, что колесо жесткое, а износу подвергается шестерня. Далее предполагается, что шестерня жесткая, а износу подвергается колесо и т.д. (фиг.3а, б, в). На этом этапе удалось получить правдоподобный износ шестерни и нарастание количества особых точек в процессе износа, а также искажение линии зацепления, подобно описанной в [3]. Дальнейший износ пары (фиг.3 е) можно предположить: более жесткая шестерня сохраняет выпуклый профиль, менее жесткое колесо разрушается под действием попеременно истирания, возникновения особых точек и разрушения в них под действием контактных напряжений и т.д. Естественным продолжением этого процесса является существенное изменение профиля зуба колеса. В приведенных в статье фигурах изношенные зубья колеса имеют вогнутый профиль. Отдельно следует отметить две особенности процесса, которые не поддаются описанной формализованной процедуре. Первая – всплеск контактных напряжений при входе пары в зацепление и выходе из него (фиг.3б). Эта задача может рассматриваться как аналог контактной задачи Штаермана [9] о контакте пуансона с упругой полуплоскостью. Вторая – наличие пластического течения при прохождении зацепления через полюс (фиг.3д).
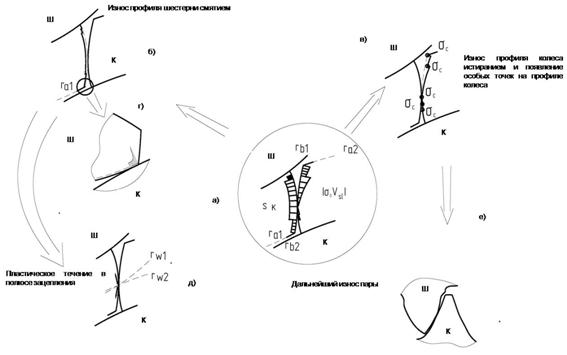
Рис. 3. Эволюция износа зубчатой пары типа B1 – P – B2.
Предложенное нами описание процесса износа подтверждается примерами, приведенными на рис.4 и рис.5.
|
Рис. 4: Износ зубчатой передачи пресса “Toledo” и сопоставление изношенной передачи с исходной. |
Рис. 5: Износ зубчатой передачи, изображенной на фиг.1с.
|
- Постановка задачи об износе заполюсной передачи с большим передаточным отношением.
В п. 1 показано, что в передаче с большим передаточным отношением источником интенсивного разрушения зубьев колеса является возникновение особой точки в полюсе зацепления в начальной фазе износа. Кроме того, вершины зубьев шестерни и ножки зубьев колеса испытывают большие контактные напряжения по сравнению с передачей с небольшим передаточным отношением (фиг.2а,б). Снижение контактных напряжений возможно, если активный участок линии зацепления удастся переместить за полюс зацепления, то есть заменить последовательность зацепления B1 – P – B2 на последовательность P – B1 – B2. Тогда формально износ зубьев колеса увеличится, но исчезнет источник разрушения в полюсе зацепления. В связи с этим можно поставить следующую задачу:
1. Определить зону наименее интенсивного износа;
2. Определить область существования возможных коэффициентов смещения x1 – x2 .
Для решения первой задачи достаточно построить производную d(s·vск /vt )/dr (фиг.6) и выбрать зону, в которой производная примерно постоянна. Этот участок имеет достаточную протяженность. Нетрудно видеть, что положение точки перегиба (inflection) функции (s·vск /vt ) зависит от передаточного отношения.
|
Рис. 6. Область существования смещений шестерни и колеса.
|
Рис. 7. Свойства заполюсной передачи
|
Вторая задача – поиск области существования смещений x1 – x2 осуществляется при естественных ограничениях x1>0.123; x2> – 4.5; ea > [ea]; sa1>[sa]. В случае, если последнее ограничение не удается выполнить, можно уменьшить диаметр окружности вершин шестерни.
В результате построена область существования смещений шестерни и колеса (фиг.7). Пример построения заполюсной передачи для х1=1, х2= – 2 и эпюры начальной фазы износа шестерни и колеса приведены на фиг.8а. Для сравнения на фиг.8б приведена передача пресса Toledo, рассчитанная для смещений х1=0.2, х2=0. В таблице 2 приведены результаты сравнения этих вариантов. В качестве объектов сравнения выбраны отношения
s1нб:s2нб и (s·vск /vt)1нб: (s·vск /vt)2нб
Таблица 2
|
|
sнб |
(s·vsl /vt)нб |
|
|
Передача |
P – B1 – B2 |
4.495 |
9.98 |
|
B1 – P – B2 |
7.892 |
6.797 |
|
|
отношение |
0.57 |
1.468 |
|
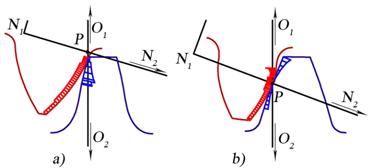
Рис. 4. Сравнение эпюр износа заполюсной передачи и передачи, рассчитанной по принятым рекомендациям.
Заключение
1. Показано, что для открытых зубчатых передач с большим передаточным отношением и полюсом зацепления, расположенным внутри активной линии зацепления, является характерными вероятность повышенного износа шестерни по контактным напряжениям и колеса – по диссипации энергии в момент входа пары в зацепление. Развитие износа колеса определяется возникновением особой точки в полюсе зацепления.
2. Предложена попытка создания зацепления, у которого полюс зацепления расположен вне активной линии зацепления – заполюсной передачи. В качестве критерия положен участок постоянного градиента функции аналога диссипации энергии. Построена область существования смещений шестерни и колеса для такой передачи.
3. Приведен пример построения заполюсной передачи. К достоинствам заполюсной передачи по сравнению с обычной следует отнести существенно пониженный уровень контактных напряжений на профиле шестерни и минимальный уровень диссипации энергии при входе зуба колеса в зацепление. К недостаткам передачи следует отнести более высокий уровень диссипации энергии при выходе зуба колеса из зацепления, а так же меньшая длина активного профиля зуба колеса.
Список литературы
1. Т. Болотовская, И. Болотовский, Г. Бочаров и др.: Справочник по геометрическому расчету эвольвентных зубчатых и червячных передач / Под ред. И. Болтовского. – М.: Машгиз, 1962.
2. Borisov, A. Golovin, A. Ermakova: Some Examples from History of Machinery in TMM Teaching// Proceeding of International Symposium on History of Machines and Mechanisms, Kluwer Academic Publishers, 2004. Pp.107-118.
3. Golovin, A. Borisov, I. Drozdova, B. Shuman: The simulating models of a gearing wear // Proceeding of CK2005, International Workshop on Computational Kinematics, Cassino, May 4-6, 2005. Paper XX-CK2005
4. Golovin: Попытка дать представление о возможных механизмах износа кинематических пар в курсе ТММ для студентов 4-го семестра //Сб. трудов симпозиума «Гидродинамическая теория смазки – 120 лет»/ Орловский государственный университет, г. Орел, 18-20 мая 2006 г., т.2, Сс.43-51 (in Russian)
5. D. Moor: Basics of tribology application. Translated from Engish by “Mir” Press, 1978. -487 p., il. (in Russian)
6. F. Barwell: Lubrication of bearing. Butterworths, London, 1956
7. V. Starzhinsky, V. Antonyuk, M. Kane and other Dictionary – Reference Book on gearing: Russian –English-German-French / 4th edition corrected and enlarged / Edited by V. Starzhinsky. – Minsk: BelGISS, 2007. – 186 p.
8. Л. Решетов: Расчет эвольвентной зубчатой передачи. Москва – Ленинград, 1935. -144 с.
9. Н. Безухов: Теория упругости и пластичности, Москва, 1953. – 420 с.
Публикации с ключевыми словами: математическая модель, эвольвентная зубчатая передача
Публикации со словами: математическая модель, эвольвентная зубчатая передача
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||







